11.1三角形的高、中线、角平分线及稳定性课件
文档属性
| 名称 | 11.1三角形的高、中线、角平分线及稳定性课件 |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-07 23:49:39 | ||
图片预览


文档简介
课件24张PPT。11.1.2 三角形的高、
中线与角平分线
11.1.3 三角形的稳定性1.掌握三角形中三条重要的线段的概念;
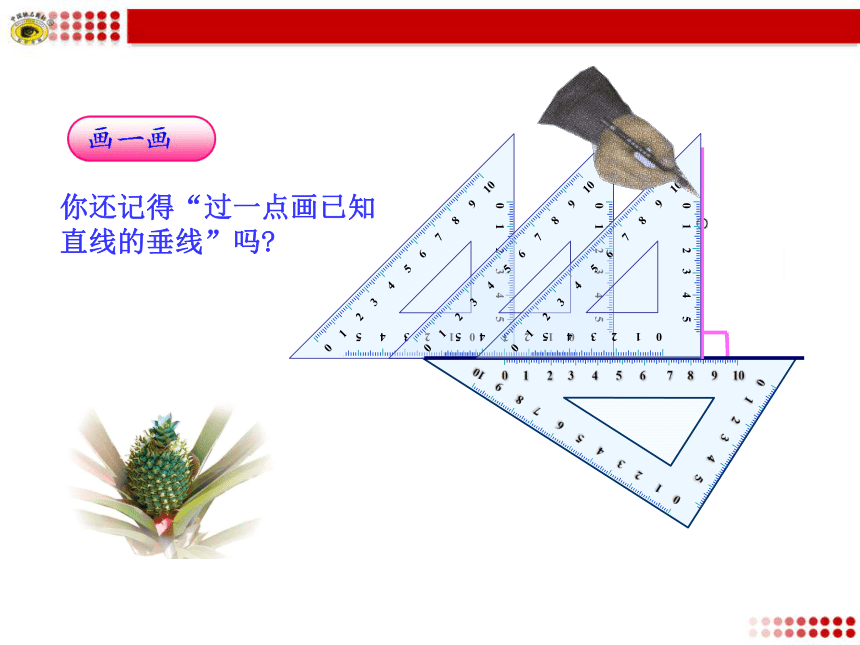
2.了解三角形的稳定性在日常生活中的应用.你还记得“过一点画已知
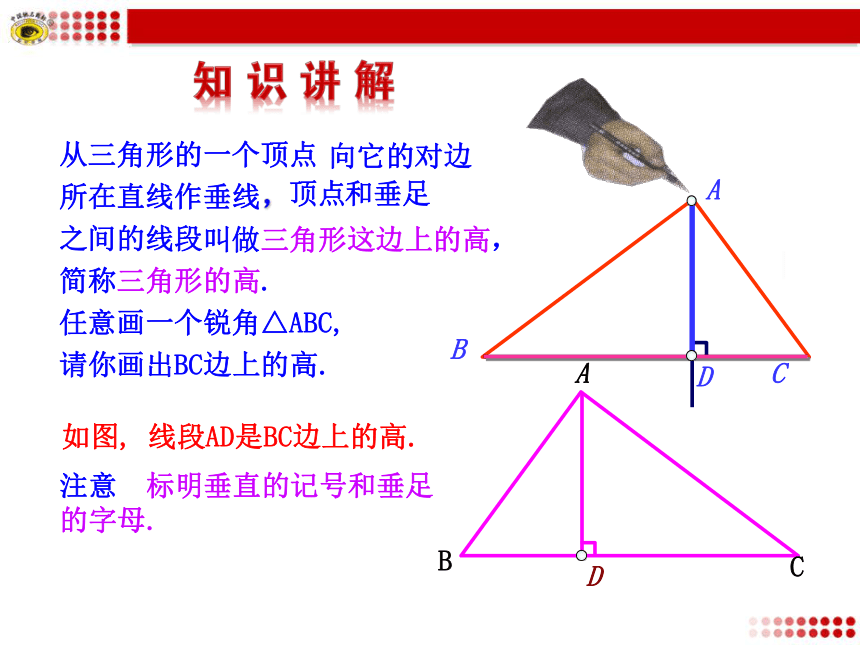
直线的垂线”吗?从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边上的高,简称三角形的高.如图, 线段AD是BC边上的高.任意画一个锐角△ABC,请你画出BC边上的高.注意 标明垂直的记号和垂足的字母.ABC锐角三角形的三条高每人画一个锐角三角形.
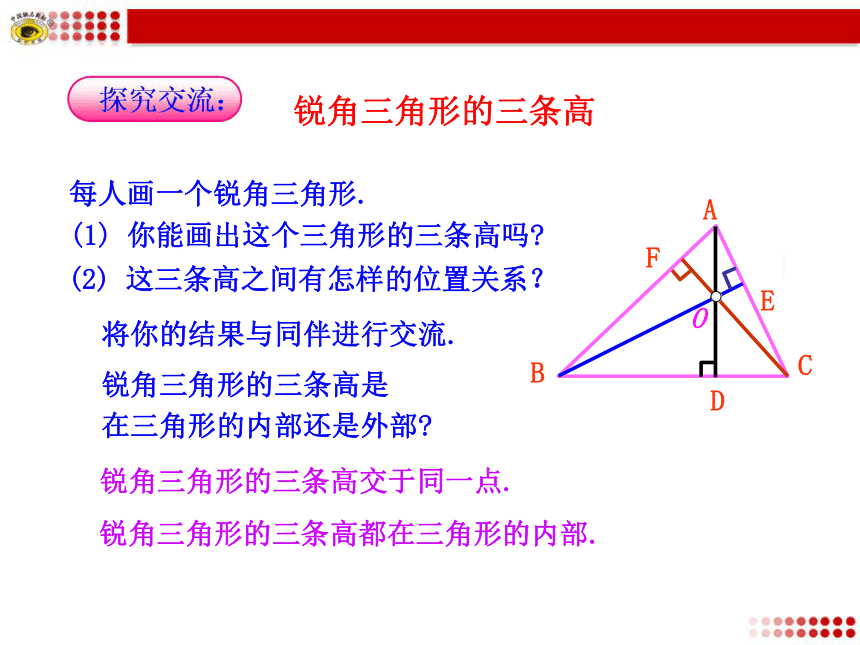
(1) 你能画出这个三角形的三条高吗?(2) 这三条高之间有怎样的位置关系?将你的结果与同伴进行交流.锐角三角形的三条高是
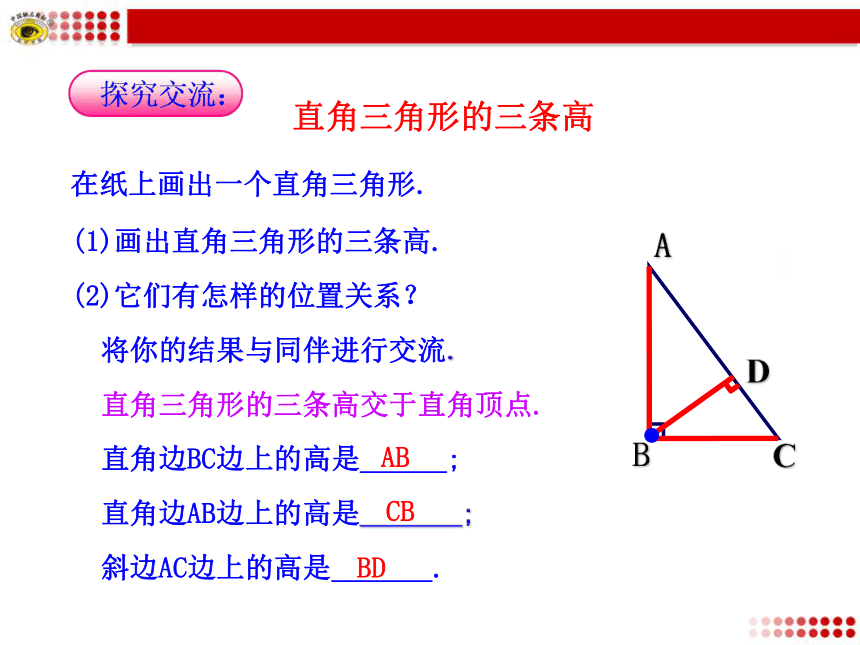
在三角形的内部还是外部?ABCDEF锐角三角形的三条高交于同一点.锐角三角形的三条高都在三角形的内部.直角三角形的三条高在纸上画出一个直角三角形.将你的结果与同伴进行交流.ABC(1)画出直角三角形的三条高.直角边BC边上的高是______; AB直角边AB边上的高是 ;CB(2)它们有怎样的位置关系?D斜边AC边上的高是_______. BD●直角三角形的三条高交于直角顶点.ABCDEF钝角三角形的三条高(1) 钝角三角形的三条高交于
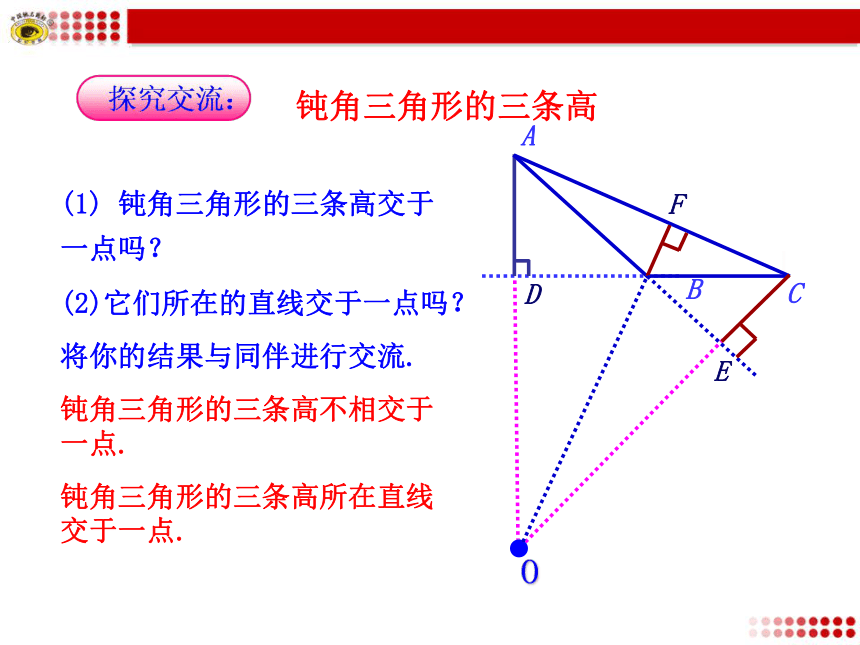
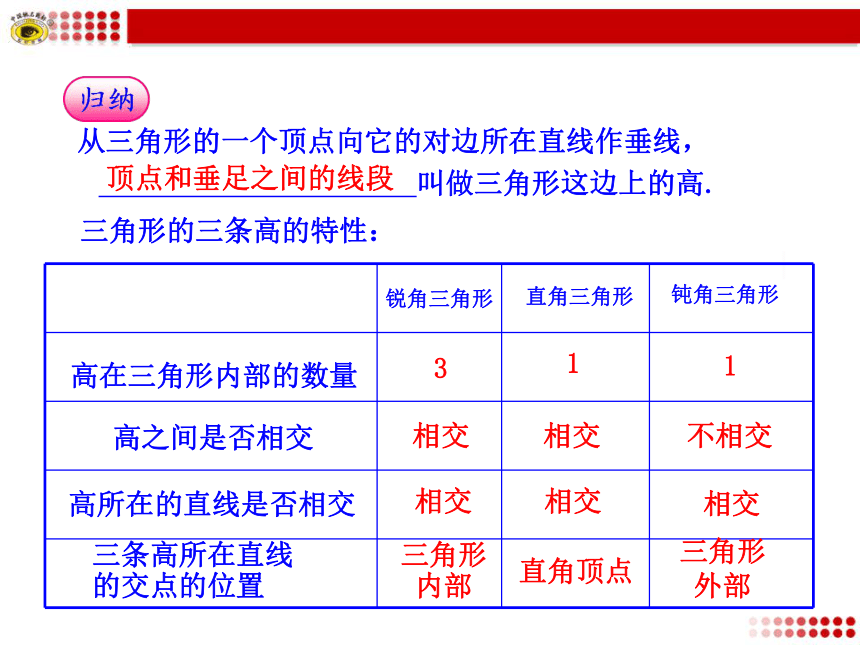
一点吗?(2)它们所在的直线交于一点吗?将你的结果与同伴进行交流.O钝角三角形的三条高不相交于一点.钝角三角形的三条高所在直线交于一点.从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段 叫做三角形这边上的高.三角形的三条高的特性:高所在的直线是否相交高之间是否相交高在三角形内部的数量钝角三角形直角三角形锐角三角形311相交相交不相交相交相交相交三条高所在直线的交点的位置三角形
内部直角顶点三角形
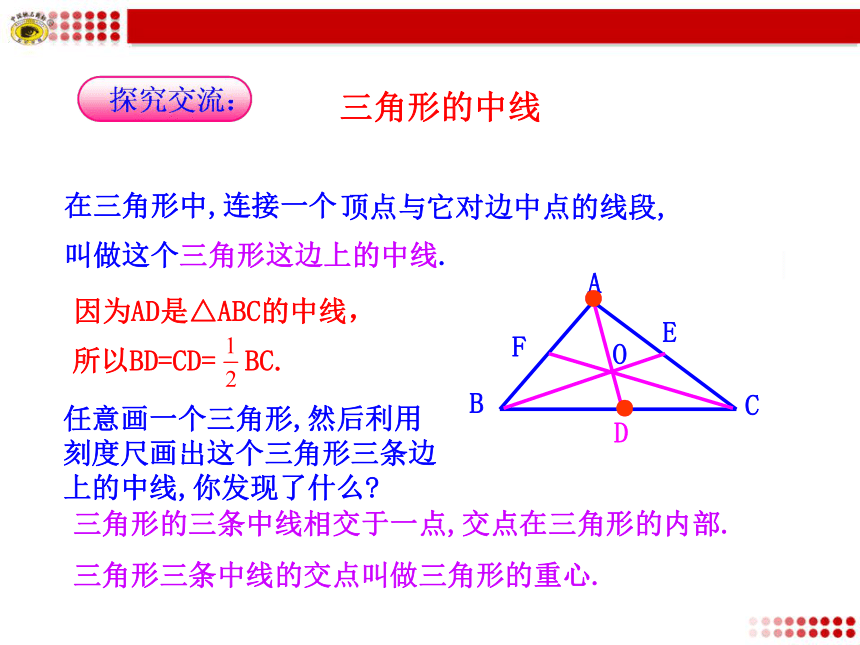
外部三角形的中线在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形这边上的中线.D因为AD是△ABC的中线,任意画一个三角形,然后利用刻度尺画出这个三角形三条边上的中线,你发现了什么?●●EFO三角形的三条中线相交于一点,交点在三角形的内部.
三角形三条中线的交点叫做三角形的重心.所以BD=CD= BC.叫做三角形的角平分线.ABCD因为AD是△ABC的角平分线,任意画一个三角形,然后利用量角器画出这个三角形三个角的角平分线,你发现了什么?●●在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,三角形的三条角平分线相交于一点,交点在三角形的内部.ACBFEDO因为BE是△ABC的角平分线,所以______=________= _____.所以∠ACB=2____ =2_____.∠ABE∠CBE∠ABC∠ACF因为CF是△ABC的角平分线,∠BCF 三角形的角平分线与角的平分线有什么区别?三角形的角平分线是一条线段,角的平分线是一条射线.2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )A.锐角三角形 B.直角三角形
C.钝角三角形 D.任意三角形1.下列各组图形中,哪一组图形中的AD是△ABC 的高( )BD三角形的稳定性三角形具有稳定性,
四边形没有稳定性. 盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,为什么要这样做呢?三角形的稳定性 将四边形木架上再钉一根木条,将它的一对顶点连接起来,然后再扭动它,这时木架的形状会改变吗?为什么? 不会改变.钉上的木条将四边形分成两个三角形,而三角形具有稳定性.斜梁斜梁直 梁三角形的稳定性如图,工人师傅砌门时,常用木条EF,EG固定门框ABCD,使其不变形,这种做法根据的是三角形的稳定性.三角形的稳定性四边形不稳定性的应用活动挂架1.下列图形中具有稳定性的是( )A.正方形 B.长方形
C.直角三角形 D.平行四边形C2.要使下列木架稳定各至少需要多少根木棍?【解析】选A.四边形没有稳定性.1.下列设备,没有利用三角形的稳定性的是( )
A.活动的四边形衣架
B.起重机
C.屋顶三角形钢架
D.索道支架2.(连云港·中考)小华在电话中问小明:“已知一个三角形三边长分别是4,9,12,如何求这个三角形的面积?”小明提示说:“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的是
( )【解析】选C.A,D项作的不是三角形的高,B项作的是三角形的高,但不是最长边上的高.3.如图,在ΔABC中,AE是中线,
AD是角平分线,AF是高.填空:
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= =90°;
(4)SΔABC= .CEBC∠CAD∠BAC∠AFCBC?AF4.如图,在△ABC中, ∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,CF⊥AD于H,判断下列说法哪些是正确的,哪些是错误的.⌒⌒ABCDE12FGH①AD是△ABE的角平分线( )②BE是△ ABD边AD上的中线( )③BE是△ ABC边AC上的中线( )④CH是△ ACD边AD上的高( )三角形的高、中线与角平分线都是线段.×××√1.三角形的三条重要线段:高、中线、角平分线.2.三角形的稳定性.通过本课时的学习,需要我们掌握: 理想是指路明星。没有理想,就没有坚定的方向,而没有方向, 就没有生活.
中线与角平分线
11.1.3 三角形的稳定性1.掌握三角形中三条重要的线段的概念;
2.了解三角形的稳定性在日常生活中的应用.你还记得“过一点画已知
直线的垂线”吗?从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边上的高,简称三角形的高.如图, 线段AD是BC边上的高.任意画一个锐角△ABC,请你画出BC边上的高.注意 标明垂直的记号和垂足的字母.ABC锐角三角形的三条高每人画一个锐角三角形.
(1) 你能画出这个三角形的三条高吗?(2) 这三条高之间有怎样的位置关系?将你的结果与同伴进行交流.锐角三角形的三条高是
在三角形的内部还是外部?ABCDEF锐角三角形的三条高交于同一点.锐角三角形的三条高都在三角形的内部.直角三角形的三条高在纸上画出一个直角三角形.将你的结果与同伴进行交流.ABC(1)画出直角三角形的三条高.直角边BC边上的高是______; AB直角边AB边上的高是 ;CB(2)它们有怎样的位置关系?D斜边AC边上的高是_______. BD●直角三角形的三条高交于直角顶点.ABCDEF钝角三角形的三条高(1) 钝角三角形的三条高交于
一点吗?(2)它们所在的直线交于一点吗?将你的结果与同伴进行交流.O钝角三角形的三条高不相交于一点.钝角三角形的三条高所在直线交于一点.从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段 叫做三角形这边上的高.三角形的三条高的特性:高所在的直线是否相交高之间是否相交高在三角形内部的数量钝角三角形直角三角形锐角三角形311相交相交不相交相交相交相交三条高所在直线的交点的位置三角形
内部直角顶点三角形
外部三角形的中线在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形这边上的中线.D因为AD是△ABC的中线,任意画一个三角形,然后利用刻度尺画出这个三角形三条边上的中线,你发现了什么?●●EFO三角形的三条中线相交于一点,交点在三角形的内部.
三角形三条中线的交点叫做三角形的重心.所以BD=CD= BC.叫做三角形的角平分线.ABCD因为AD是△ABC的角平分线,任意画一个三角形,然后利用量角器画出这个三角形三个角的角平分线,你发现了什么?●●在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,三角形的三条角平分线相交于一点,交点在三角形的内部.ACBFEDO因为BE是△ABC的角平分线,所以______=________= _____.所以∠ACB=2____ =2_____.∠ABE∠CBE∠ABC∠ACF因为CF是△ABC的角平分线,∠BCF 三角形的角平分线与角的平分线有什么区别?三角形的角平分线是一条线段,角的平分线是一条射线.2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )A.锐角三角形 B.直角三角形
C.钝角三角形 D.任意三角形1.下列各组图形中,哪一组图形中的AD是△ABC 的高( )BD三角形的稳定性三角形具有稳定性,
四边形没有稳定性. 盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,为什么要这样做呢?三角形的稳定性 将四边形木架上再钉一根木条,将它的一对顶点连接起来,然后再扭动它,这时木架的形状会改变吗?为什么? 不会改变.钉上的木条将四边形分成两个三角形,而三角形具有稳定性.斜梁斜梁直 梁三角形的稳定性如图,工人师傅砌门时,常用木条EF,EG固定门框ABCD,使其不变形,这种做法根据的是三角形的稳定性.三角形的稳定性四边形不稳定性的应用活动挂架1.下列图形中具有稳定性的是( )A.正方形 B.长方形
C.直角三角形 D.平行四边形C2.要使下列木架稳定各至少需要多少根木棍?【解析】选A.四边形没有稳定性.1.下列设备,没有利用三角形的稳定性的是( )
A.活动的四边形衣架
B.起重机
C.屋顶三角形钢架
D.索道支架2.(连云港·中考)小华在电话中问小明:“已知一个三角形三边长分别是4,9,12,如何求这个三角形的面积?”小明提示说:“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的是
( )【解析】选C.A,D项作的不是三角形的高,B项作的是三角形的高,但不是最长边上的高.3.如图,在ΔABC中,AE是中线,
AD是角平分线,AF是高.填空:
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= =90°;
(4)SΔABC= .CEBC∠CAD∠BAC∠AFCBC?AF4.如图,在△ABC中, ∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,CF⊥AD于H,判断下列说法哪些是正确的,哪些是错误的.⌒⌒ABCDE12FGH①AD是△ABE的角平分线( )②BE是△ ABD边AD上的中线( )③BE是△ ABC边AC上的中线( )④CH是△ ACD边AD上的高( )三角形的高、中线与角平分线都是线段.×××√1.三角形的三条重要线段:高、中线、角平分线.2.三角形的稳定性.通过本课时的学习,需要我们掌握: 理想是指路明星。没有理想,就没有坚定的方向,而没有方向, 就没有生活.
