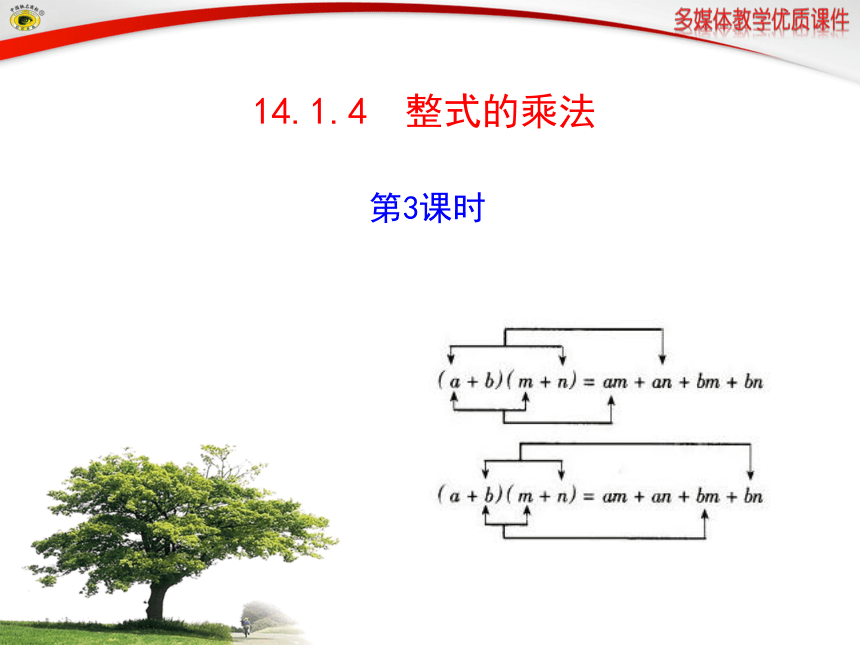
14.1.4 整式的乘法 第3课时
文档属性
| 名称 | 14.1.4 整式的乘法 第3课时 |
|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-09 00:00:00 | ||
图片预览









文档简介
课件21张PPT。第3课时14.1.4 整式的乘法1.理解并掌握多项式乘以多项式的法则.3.培养数学感知,体验数学在实际应用中的价值,树立良好的学习态度.2.经历探索多项式与多项式相乘的过程,通过导图,理解多项式与多项式相乘的结果,能够按多项式乘法步骤进行简单的多项式乘法的运算,达到熟练进行多项式的乘法运算的目的. 计算:1.单项式乘以单项式2.单项式乘以多项式问题:为了扩大街心花园的绿地面积,把一块原长a m,宽p m的长方形绿地,加长了b m,加宽了q m.你能用几种方法求出扩大后的绿地面积?【解析】扩大后的绿地可以看成长为(a+b)m,宽为(p+q)m的长方形,所以这块绿地的面积为(a+b)(p+q)m2. 扩大后的绿地还可以看成由四个小长方形组成,所以
这块绿地的面积为(ap+aq+bp+bq)m2.因此,(a+b)( p+q)=ap+aq+bp+bq多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.(a+b)( p+q)=ap+aq+bp+bq(a+b+c)(p+q)=ap+aq+bp+bq+cp+cq【例1】计算 :
(3x+1)(x-2); (2)(x-8y)(x-y).【解析】(1)(3x+1)(x-2)
= (3x)?x+(3x)?(-2)+1?x+1×(-2)
= 3x2-6x+x-2
=3x2-5x-2.(x-8y)(x-y)
= x2-xy-8xy+8y2
= x2-9xy +8y2.注意:1.不要漏乘
2.注意符号
3.结果化为最简形式【例题】(3)(x+y)(2x–y)(3x+2y).(x+y)2. (2) (x+y)(x2y+y2).【例2】计算(3)原式=(2x2-xy+2xy-y2)(3x+2y )
=(2x2+xy-y2)(3x+2y)
=6x3+4x2y+3x2y+2xy2-3xy2-2y3
=6x3 +7x2y-xy2-2y3 . 【解析】(1)原式=(x+y)(x+y)
=x2+ xy+ xy+ y2
=x2+ 2xy+ y2.(2)原式=x3y+ xy2+x2y2+y3.计算
(1) (2x+1)(x+3). (2) (m+2n)(m+3n).
(3) (a-1)2 . (4) (a+3b)(a–3b ).
答案: (1) 2x2+7x+3. (2) m2+5mn+6n2.
(3) a2-2a+1. (4) a2-9b2.看谁做得又快又对【跟踪训练】 (x+2)(x+3) = x2 + 5x+6;
(x-4)(x+1) = x2–3x-4;
(y+4)(y-2) = y2 +2y-8;
(y-5)(y-3) = y2- 8y+15.观察上述式子,你可以 得出一个什么规律吗? (x+p)(x+q) = x2 + (p+q) x + p q 确定下列各式中m的值:(口答)
(1)(x+4)(x+9)= x2 + m x + 36
(2)(x-2)(x-18)=x2 + m x + 36
(3)(x+3)(x+p) =x2+ m x + 36
(4)(x-6)(x-p)=x2+ m x + 36 (1) m =13 (2) m = -20 (3) p =12, m=15 (4) p= 6, m= -12温馨提示:
(1)利用下式
(x+p)(x+q)=x2+(p+q)x+pq
(2)注意符号【规律方法】注意:多项式与多项式相乘.
1.必须做到不重复,不遗漏.2.确定积中每一项的符号.3.结果应化为最简式即合并同类项.(1)一个多项式乘以一个多项式仍是多项式.( ) (2)(a-b)(a2b-1)=a3b-a-a2b2. ( )(3)已知a>b>0,在边长为a+b的正方形内,挖去一个边长为a-b的正方形,剩余部分的面积为4ab.( ) 1.判断: √ ×√A.2.(临沂·中考)若,,的值等于( )B.C.D.B则代数式3.(日照·中考)由m(a+b+c)=ma+mb+mc,可得:
(a+b)(a2-ab+b2)=a3-a2b+ab2+a2b-ab2+b3=a3+b3,
即(a+b)(a2-ab+b2)=a3+b3.①
我们把等式①叫做多项式乘法的立方公式.
下列应用这个立方公式进行的变形不正确的是( )
A.(x+4y)(x2-4xy+16y2)=x3+64y3
B.(2x+y)(4x2-2xy+y2)=8x3+y3
C.(a+1)(a2+a+1)=a3+1
D.x3+27=(x+3)(x2-3x+9)C4.计算:(3a–2)(a–1)–(a+1)(a+2); 【解析】(3a–2)(a–1)–(a+1)(a+2)是多项式的积与积的差,后两个多项式乘积的展开式要用括号括起来.结果为:2a2-8a.2c a+b ca- b5.如图,在长方形地中有两条小路.依据图中标注的数据,计算绿地的面积?(a>b)【解析】(a+b)(a-b)-(a+b)c-2c(a-b)+2c2
=a2-b2+bc-3ac+2c26.求长方体的体积?(a>b) a+2ba+b长方体a-b【解析】(a+2b)(a-b)(a+b)=a3-2b3+2a2b-ab2(a+b)(p+q)=ap+bp+aq+bq(a+b+c)(p+q)=ap+aq+bp+bq+cp+cq 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.多项式与多项式相乘的法则:(x+p)(x+q)=x2+(p+q)x+pq智慧的可靠标志就是能够在平凡中发现奇迹.
——爱默生
这块绿地的面积为(ap+aq+bp+bq)m2.因此,(a+b)( p+q)=ap+aq+bp+bq多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.(a+b)( p+q)=ap+aq+bp+bq(a+b+c)(p+q)=ap+aq+bp+bq+cp+cq【例1】计算 :
(3x+1)(x-2); (2)(x-8y)(x-y).【解析】(1)(3x+1)(x-2)
= (3x)?x+(3x)?(-2)+1?x+1×(-2)
= 3x2-6x+x-2
=3x2-5x-2.(x-8y)(x-y)
= x2-xy-8xy+8y2
= x2-9xy +8y2.注意:1.不要漏乘
2.注意符号
3.结果化为最简形式【例题】(3)(x+y)(2x–y)(3x+2y).(x+y)2. (2) (x+y)(x2y+y2).【例2】计算(3)原式=(2x2-xy+2xy-y2)(3x+2y )
=(2x2+xy-y2)(3x+2y)
=6x3+4x2y+3x2y+2xy2-3xy2-2y3
=6x3 +7x2y-xy2-2y3 . 【解析】(1)原式=(x+y)(x+y)
=x2+ xy+ xy+ y2
=x2+ 2xy+ y2.(2)原式=x3y+ xy2+x2y2+y3.计算
(1) (2x+1)(x+3). (2) (m+2n)(m+3n).
(3) (a-1)2 . (4) (a+3b)(a–3b ).
答案: (1) 2x2+7x+3. (2) m2+5mn+6n2.
(3) a2-2a+1. (4) a2-9b2.看谁做得又快又对【跟踪训练】 (x+2)(x+3) = x2 + 5x+6;
(x-4)(x+1) = x2–3x-4;
(y+4)(y-2) = y2 +2y-8;
(y-5)(y-3) = y2- 8y+15.观察上述式子,你可以 得出一个什么规律吗? (x+p)(x+q) = x2 + (p+q) x + p q 确定下列各式中m的值:(口答)
(1)(x+4)(x+9)= x2 + m x + 36
(2)(x-2)(x-18)=x2 + m x + 36
(3)(x+3)(x+p) =x2+ m x + 36
(4)(x-6)(x-p)=x2+ m x + 36 (1) m =13 (2) m = -20 (3) p =12, m=15 (4) p= 6, m= -12温馨提示:
(1)利用下式
(x+p)(x+q)=x2+(p+q)x+pq
(2)注意符号【规律方法】注意:多项式与多项式相乘.
1.必须做到不重复,不遗漏.2.确定积中每一项的符号.3.结果应化为最简式即合并同类项.(1)一个多项式乘以一个多项式仍是多项式.( ) (2)(a-b)(a2b-1)=a3b-a-a2b2. ( )(3)已知a>b>0,在边长为a+b的正方形内,挖去一个边长为a-b的正方形,剩余部分的面积为4ab.( ) 1.判断: √ ×√A.2.(临沂·中考)若,,的值等于( )B.C.D.B则代数式3.(日照·中考)由m(a+b+c)=ma+mb+mc,可得:
(a+b)(a2-ab+b2)=a3-a2b+ab2+a2b-ab2+b3=a3+b3,
即(a+b)(a2-ab+b2)=a3+b3.①
我们把等式①叫做多项式乘法的立方公式.
下列应用这个立方公式进行的变形不正确的是( )
A.(x+4y)(x2-4xy+16y2)=x3+64y3
B.(2x+y)(4x2-2xy+y2)=8x3+y3
C.(a+1)(a2+a+1)=a3+1
D.x3+27=(x+3)(x2-3x+9)C4.计算:(3a–2)(a–1)–(a+1)(a+2); 【解析】(3a–2)(a–1)–(a+1)(a+2)是多项式的积与积的差,后两个多项式乘积的展开式要用括号括起来.结果为:2a2-8a.2c a+b ca- b5.如图,在长方形地中有两条小路.依据图中标注的数据,计算绿地的面积?(a>b)【解析】(a+b)(a-b)-(a+b)c-2c(a-b)+2c2
=a2-b2+bc-3ac+2c26.求长方体的体积?(a>b) a+2ba+b长方体a-b【解析】(a+2b)(a-b)(a+b)=a3-2b3+2a2b-ab2(a+b)(p+q)=ap+bp+aq+bq(a+b+c)(p+q)=ap+aq+bp+bq+cp+cq 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.多项式与多项式相乘的法则:(x+p)(x+q)=x2+(p+q)x+pq智慧的可靠标志就是能够在平凡中发现奇迹.
——爱默生
