北师大版数学七年级下册第5章生活中的轴对称 单元综合检测(word版含答案)
文档属性
| 名称 | 北师大版数学七年级下册第5章生活中的轴对称 单元综合检测(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 208.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-16 17:06:02 | ||
图片预览


文档简介
第五章综合检测
一、选择题(本大题共10小题,每小题3分,共30分)
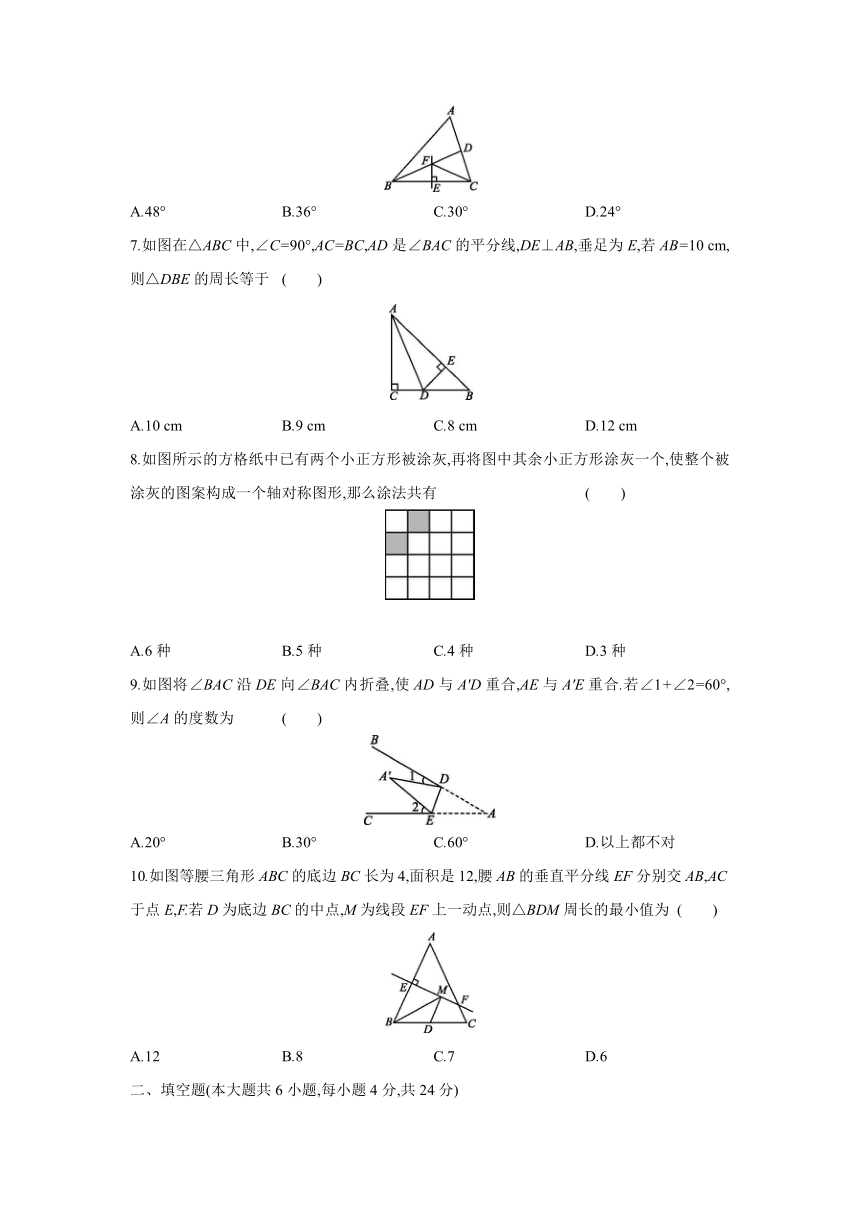
1.下面四个手机应用图标中是轴对称图形的是 ( )
2.如图若△ABC与△A'B'C'关于直线MN对称,BB'交MN于点O,则下列说法中不一定正确的是 ( )
A.AC=A'C' B.AB∥B'C' C.AA'⊥MN D.BO=B'O
3.如图直线m表示一条河,M,N表示两个村庄,欲在m上的某处修建一个给水站,向两个村庄供水,现有如图所示的四种铺设管道的方案,图中实线表示铺设的管道,则所需管道最短的方案是 ( )
4.如图l∥m,等边三角形ABC的顶点B在直线m上,∠1=20°,则∠2的度数为 ( )
A.60° B.45° C.40° D.30°
5.如图在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为( )
A.35° B.40° C.45° D.50°
6.如图在△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为 ( )
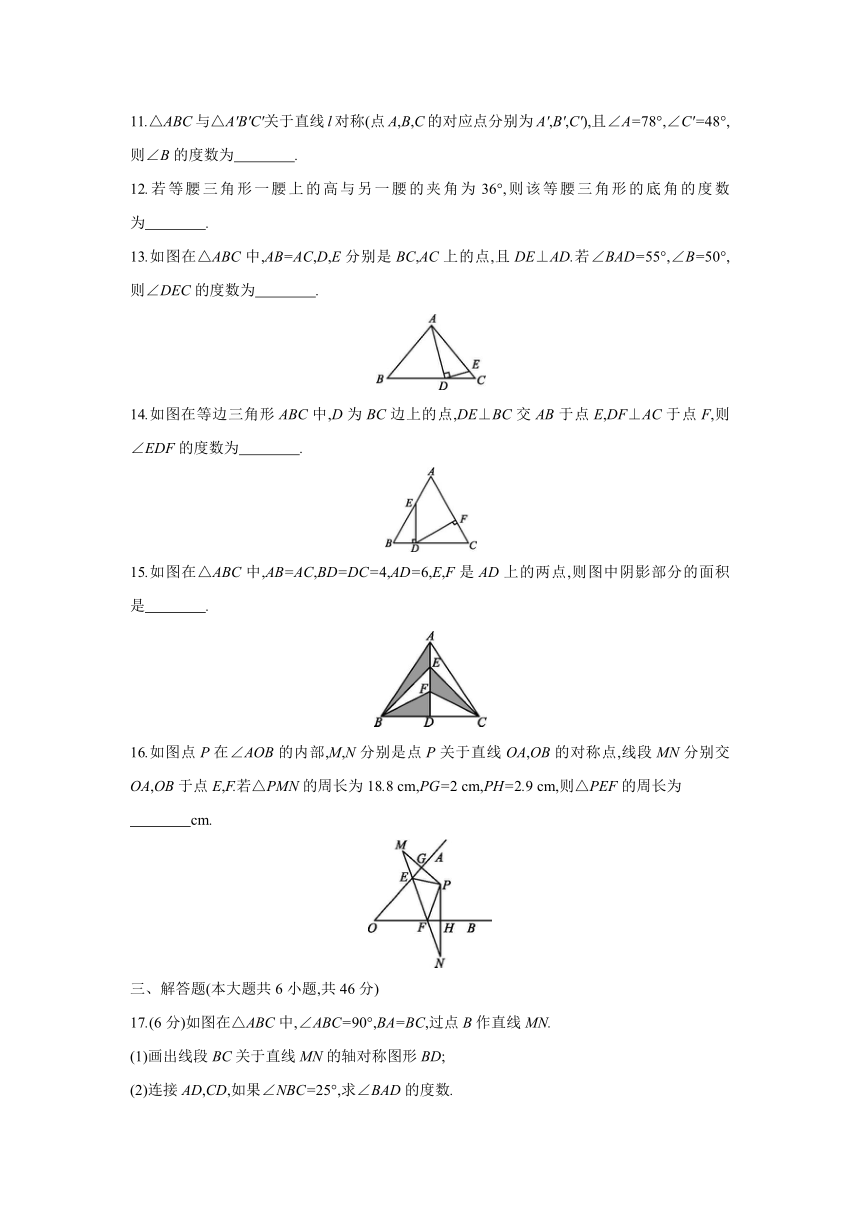
A.48° B.36° C.30° D.24°
7.如图在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=10 cm,则△DBE的周长等于 ( )
A.10 cm B.9 cm C.8 cm D.12 cm
8.如图所示的方格纸中已有两个小正方形被涂灰,再将图中其余小正方形涂灰一个,使整个被涂灰的图案构成一个轴对称图形,那么涂法共有 ( )
A.6种 B.5种 C.4种 D.3种
9.如图将∠BAC沿DE向∠BAC内折叠,使AD与A'D重合,AE与A'E重合.若∠1+∠2=60°,则∠A的度数为 ( )
A.20° B.30° C.60° D.以上都不对
10.如图等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB,AC于点E,F.若D为底边BC的中点,M为线段EF上一动点,则△BDM周长的最小值为 ( )
A.12 B.8 C.7 D.6
二、填空题(本大题共6小题,每小题4分,共24分)
11.△ABC与△A'B'C'关于直线l对称(点A,B,C的对应点分别为A',B',C'),且∠A=78°,∠C'=48°,则∠B的度数为 .
12.若等腰三角形一腰上的高与另一腰的夹角为36°,则该等腰三角形的底角的度数为 .
13.如图在△ABC中,AB=AC,D,E分别是BC,AC上的点,且DE⊥AD.若∠BAD=55°,∠B=50°,则∠DEC的度数为 .
14.如图在等边三角形ABC中,D为BC边上的点,DE⊥BC交AB于点E,DF⊥AC于点F,则∠EDF的度数为 .
15.如图在△ABC中,AB=AC,BD=DC=4,AD=6,E,F是AD上的两点,则图中阴影部分的面积是 .
16.如图点P在∠AOB的内部,M,N分别是点P关于直线OA,OB的对称点,线段MN分别交OA,OB于点E,F.若△PMN的周长为18.8 cm,PG=2 cm,PH=2.9 cm,则△PEF的周长为
cm.
三、解答题(本大题共6小题,共46分)
17.(6分)如图在△ABC中,∠ABC=90°,BA=BC,过点B作直线MN.
(1)画出线段BC关于直线MN的轴对称图形BD;
(2)连接AD,CD,如果∠NBC=25°,求∠BAD的度数.
18.(6分)如图点M和点N在∠AOB内部.
(1)请你作出点P,使点P到点M和点N的距离相等,且到∠AOB两边的距离也相等(保留作图痕迹,不写作法);
(2)请说明作图理由.
19.(7分)如图CE⊥AB于点E,BD⊥AC于点D,BD,CE交于点O,且AO平分∠BAC.试说明:OB=OC.
20.(8分)如图在△ABC中,AB=AC,D是BC边上的中点,DE⊥AB于点E,DF⊥AC于点F.试说明:DE=DF.
21.(9分)如图所示,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D.
(1)若BC=10,BD=6,则点D到AB的距离是多少
(2)若∠BAD=30°,求∠B的度数.
22.(10分)如图E,F分别是等边三角形ABC的边AB,AC上的点,且BE=AF,CE,BF交于点P.
(1)试说明:CE=BF;
(2)求∠BPC的度数.
答案
1.D 2.B 3.D
4.C 因为△ABC为等边三角形,
所以∠ACB=60°.
如图,过点C作CD∥l.
因为l∥m,所以l∥m∥CD,
所以∠2=∠ACD,∠1=∠DCB,
所以∠1+∠2=∠ACB.
又因为∠1=20°,所以∠2=40°.故选C.
5.A 6.A 7.A 8.A
9.B 10.B
11.54° 因为△ABC与△A'B'C'关于直线l对称,
所以∠C=∠C'=48°,所以∠B=180°-78°-48°=54°.
12.63°或27°
13.115° 14.60° 15.12 16.9
17.解:(1)如图所示,BD即为所求.
(2)由题意可知BC=BD,∠NBD=∠NBC=25°.
因为AB=BC,所以AB=BD,所以∠BAD=∠BDA.因为∠ABD=∠ABC+∠NBC+∠NBD=140°,
所以∠BAD=(180°-∠ABD)=20°.
18.解:(1)如图所示.
(2)角平分线上的点到这个角的两边的距离相等,线段垂直平分线上的点到这条线段两个端点的距离相等.
19.解:因为AO平分∠BAC,CE⊥AB,BD⊥AC,所以OE=OD,∠BEO=∠CDO=90°.
在△OBE和△OCD中,因为∠EOB=∠DOC,OE=OD,∠BEO=∠CDO,
所以△OBE≌△OCD,所以OB=OC.
20.解:连接AD.
因为AB=AC,D是BC边上的中点,
所以AD平分∠BAC.
因为DE⊥AB,DF⊥AC,
所以DE=DF.
21. (1)根据角平分线的性质,点D到AB的距离等于点D到AC的距离;(2)因为直角三角形两锐角互余,所以要求∠B的度数,可求∠BAC的度数,利用角平分线的定义易求∠BAC的度数.
解:(1)因为∠C=90°,CD=BC-BD=4,
所以点D到AC的距离为4.
根据角平分线的性质,可知点D到AB的距离等于点D到AC的距离,即为4.
(2)因为AD平分∠BAC,∠BAD=30°,
所以∠BAC=2∠BAD=60°.
又因为∠C=90°,所以∠B=180°-90°-60°=30°.
[点析] 角平分线的性质是判断线段相等的重要依据.
22. (1)欲说明CE=BF,只需说明它们所在的△BCE和△ABF全等即可;(2)欲求∠BPC的度数,根据三角形内角和等于180°,知只需求出∠PCB+∠PBC即可.
解:(1)因为△ABC是等边三角形,
所以AB=BC,∠A=∠EBC=60°.
又因为BE=AF,
所以△BCE≌△ABF,
所以CE=BF.
(2)由(1)得△BCE≌△ABF,
所以∠PCB=∠ABF,
所以∠PCB+∠PBC=∠ABF+∠PBC=∠EBC=60°.
因为∠PCB+∠PBC+∠BPC=180°,
所以∠BPC=180°-(∠PCB+∠PBC)=180°-60°=120°.
一、选择题(本大题共10小题,每小题3分,共30分)
1.下面四个手机应用图标中是轴对称图形的是 ( )
2.如图若△ABC与△A'B'C'关于直线MN对称,BB'交MN于点O,则下列说法中不一定正确的是 ( )
A.AC=A'C' B.AB∥B'C' C.AA'⊥MN D.BO=B'O
3.如图直线m表示一条河,M,N表示两个村庄,欲在m上的某处修建一个给水站,向两个村庄供水,现有如图所示的四种铺设管道的方案,图中实线表示铺设的管道,则所需管道最短的方案是 ( )
4.如图l∥m,等边三角形ABC的顶点B在直线m上,∠1=20°,则∠2的度数为 ( )
A.60° B.45° C.40° D.30°
5.如图在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为( )
A.35° B.40° C.45° D.50°
6.如图在△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为 ( )
A.48° B.36° C.30° D.24°
7.如图在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=10 cm,则△DBE的周长等于 ( )
A.10 cm B.9 cm C.8 cm D.12 cm
8.如图所示的方格纸中已有两个小正方形被涂灰,再将图中其余小正方形涂灰一个,使整个被涂灰的图案构成一个轴对称图形,那么涂法共有 ( )
A.6种 B.5种 C.4种 D.3种
9.如图将∠BAC沿DE向∠BAC内折叠,使AD与A'D重合,AE与A'E重合.若∠1+∠2=60°,则∠A的度数为 ( )
A.20° B.30° C.60° D.以上都不对
10.如图等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB,AC于点E,F.若D为底边BC的中点,M为线段EF上一动点,则△BDM周长的最小值为 ( )
A.12 B.8 C.7 D.6
二、填空题(本大题共6小题,每小题4分,共24分)
11.△ABC与△A'B'C'关于直线l对称(点A,B,C的对应点分别为A',B',C'),且∠A=78°,∠C'=48°,则∠B的度数为 .
12.若等腰三角形一腰上的高与另一腰的夹角为36°,则该等腰三角形的底角的度数为 .
13.如图在△ABC中,AB=AC,D,E分别是BC,AC上的点,且DE⊥AD.若∠BAD=55°,∠B=50°,则∠DEC的度数为 .
14.如图在等边三角形ABC中,D为BC边上的点,DE⊥BC交AB于点E,DF⊥AC于点F,则∠EDF的度数为 .
15.如图在△ABC中,AB=AC,BD=DC=4,AD=6,E,F是AD上的两点,则图中阴影部分的面积是 .
16.如图点P在∠AOB的内部,M,N分别是点P关于直线OA,OB的对称点,线段MN分别交OA,OB于点E,F.若△PMN的周长为18.8 cm,PG=2 cm,PH=2.9 cm,则△PEF的周长为
cm.
三、解答题(本大题共6小题,共46分)
17.(6分)如图在△ABC中,∠ABC=90°,BA=BC,过点B作直线MN.
(1)画出线段BC关于直线MN的轴对称图形BD;
(2)连接AD,CD,如果∠NBC=25°,求∠BAD的度数.
18.(6分)如图点M和点N在∠AOB内部.
(1)请你作出点P,使点P到点M和点N的距离相等,且到∠AOB两边的距离也相等(保留作图痕迹,不写作法);
(2)请说明作图理由.
19.(7分)如图CE⊥AB于点E,BD⊥AC于点D,BD,CE交于点O,且AO平分∠BAC.试说明:OB=OC.
20.(8分)如图在△ABC中,AB=AC,D是BC边上的中点,DE⊥AB于点E,DF⊥AC于点F.试说明:DE=DF.
21.(9分)如图所示,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D.
(1)若BC=10,BD=6,则点D到AB的距离是多少
(2)若∠BAD=30°,求∠B的度数.
22.(10分)如图E,F分别是等边三角形ABC的边AB,AC上的点,且BE=AF,CE,BF交于点P.
(1)试说明:CE=BF;
(2)求∠BPC的度数.
答案
1.D 2.B 3.D
4.C 因为△ABC为等边三角形,
所以∠ACB=60°.
如图,过点C作CD∥l.
因为l∥m,所以l∥m∥CD,
所以∠2=∠ACD,∠1=∠DCB,
所以∠1+∠2=∠ACB.
又因为∠1=20°,所以∠2=40°.故选C.
5.A 6.A 7.A 8.A
9.B 10.B
11.54° 因为△ABC与△A'B'C'关于直线l对称,
所以∠C=∠C'=48°,所以∠B=180°-78°-48°=54°.
12.63°或27°
13.115° 14.60° 15.12 16.9
17.解:(1)如图所示,BD即为所求.
(2)由题意可知BC=BD,∠NBD=∠NBC=25°.
因为AB=BC,所以AB=BD,所以∠BAD=∠BDA.因为∠ABD=∠ABC+∠NBC+∠NBD=140°,
所以∠BAD=(180°-∠ABD)=20°.
18.解:(1)如图所示.
(2)角平分线上的点到这个角的两边的距离相等,线段垂直平分线上的点到这条线段两个端点的距离相等.
19.解:因为AO平分∠BAC,CE⊥AB,BD⊥AC,所以OE=OD,∠BEO=∠CDO=90°.
在△OBE和△OCD中,因为∠EOB=∠DOC,OE=OD,∠BEO=∠CDO,
所以△OBE≌△OCD,所以OB=OC.
20.解:连接AD.
因为AB=AC,D是BC边上的中点,
所以AD平分∠BAC.
因为DE⊥AB,DF⊥AC,
所以DE=DF.
21. (1)根据角平分线的性质,点D到AB的距离等于点D到AC的距离;(2)因为直角三角形两锐角互余,所以要求∠B的度数,可求∠BAC的度数,利用角平分线的定义易求∠BAC的度数.
解:(1)因为∠C=90°,CD=BC-BD=4,
所以点D到AC的距离为4.
根据角平分线的性质,可知点D到AB的距离等于点D到AC的距离,即为4.
(2)因为AD平分∠BAC,∠BAD=30°,
所以∠BAC=2∠BAD=60°.
又因为∠C=90°,所以∠B=180°-90°-60°=30°.
[点析] 角平分线的性质是判断线段相等的重要依据.
22. (1)欲说明CE=BF,只需说明它们所在的△BCE和△ABF全等即可;(2)欲求∠BPC的度数,根据三角形内角和等于180°,知只需求出∠PCB+∠PBC即可.
解:(1)因为△ABC是等边三角形,
所以AB=BC,∠A=∠EBC=60°.
又因为BE=AF,
所以△BCE≌△ABF,
所以CE=BF.
(2)由(1)得△BCE≌△ABF,
所以∠PCB=∠ABF,
所以∠PCB+∠PBC=∠ABF+∠PBC=∠EBC=60°.
因为∠PCB+∠PBC+∠BPC=180°,
所以∠BPC=180°-(∠PCB+∠PBC)=180°-60°=120°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
