北师大版数学七年级下册第4章三角形 单元综合检测(word版含答案)
文档属性
| 名称 | 北师大版数学七年级下册第4章三角形 单元综合检测(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 224.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-16 00:00:00 | ||
图片预览



文档简介
第四章综合检测
一、选择题(本大题共10小题,每小题3分,共30分)
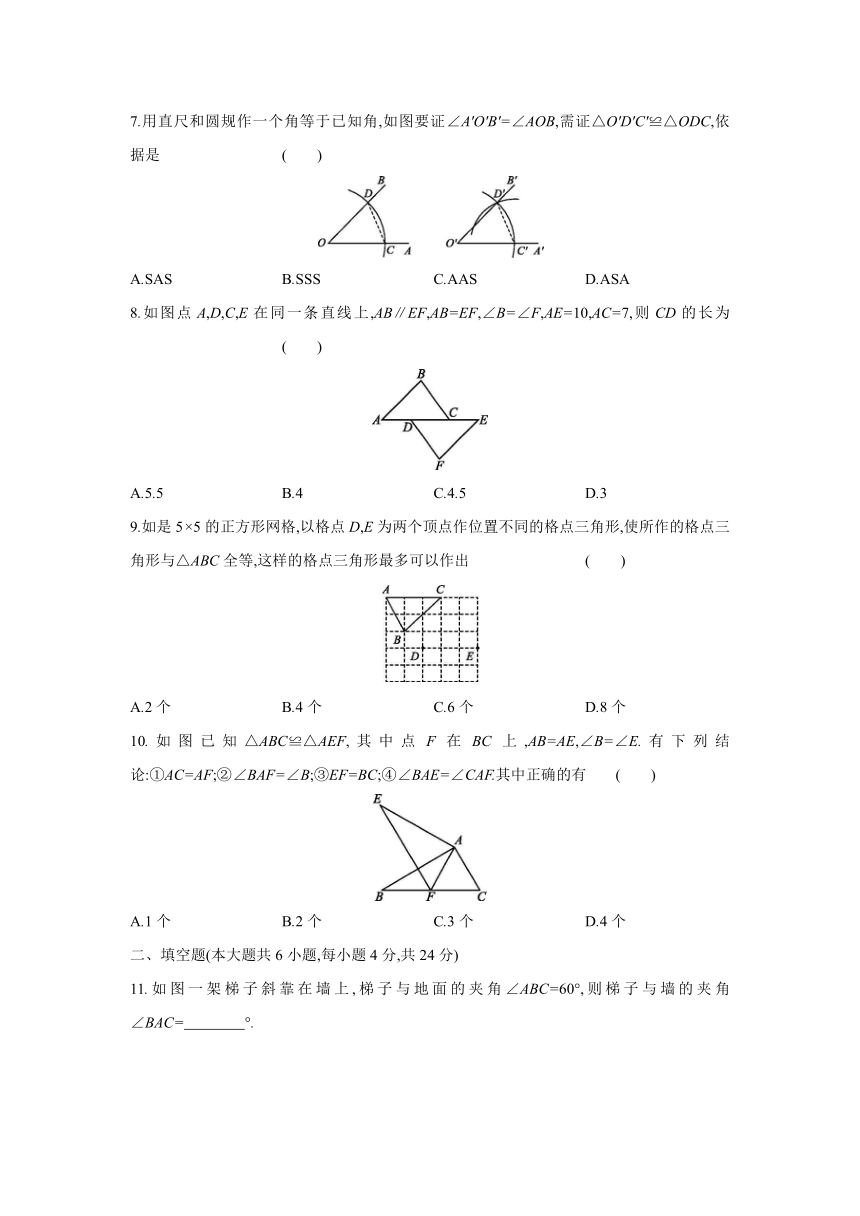
1.下列图形中与已知图形()全等的是 ( )
2.下列图形中,AD是△ABC的高的是 ( )
3.若一个三角形三个内角的度数之比为2∶3∶4,则这个三角形是 ( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
4.已知三角形的三条边长分别为4,a,8,那么该三角形的周长C的取值范围是 ( )
A.45.如图△ABC的面积为8,AD为BC边上的中线,E为AD上任意一点,连接BE,CE,图中阴影部分的面积为 ( )
A.2 B.3 C.4 D.5
6.如图在△ABC和△DEC中,AB=DE.若添加条件后使得△ABC≌△DEC,则在下列条件中,不能添加的是 ( )
A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.∠B=∠E,∠A=∠D D.BC=EC,∠A=∠D
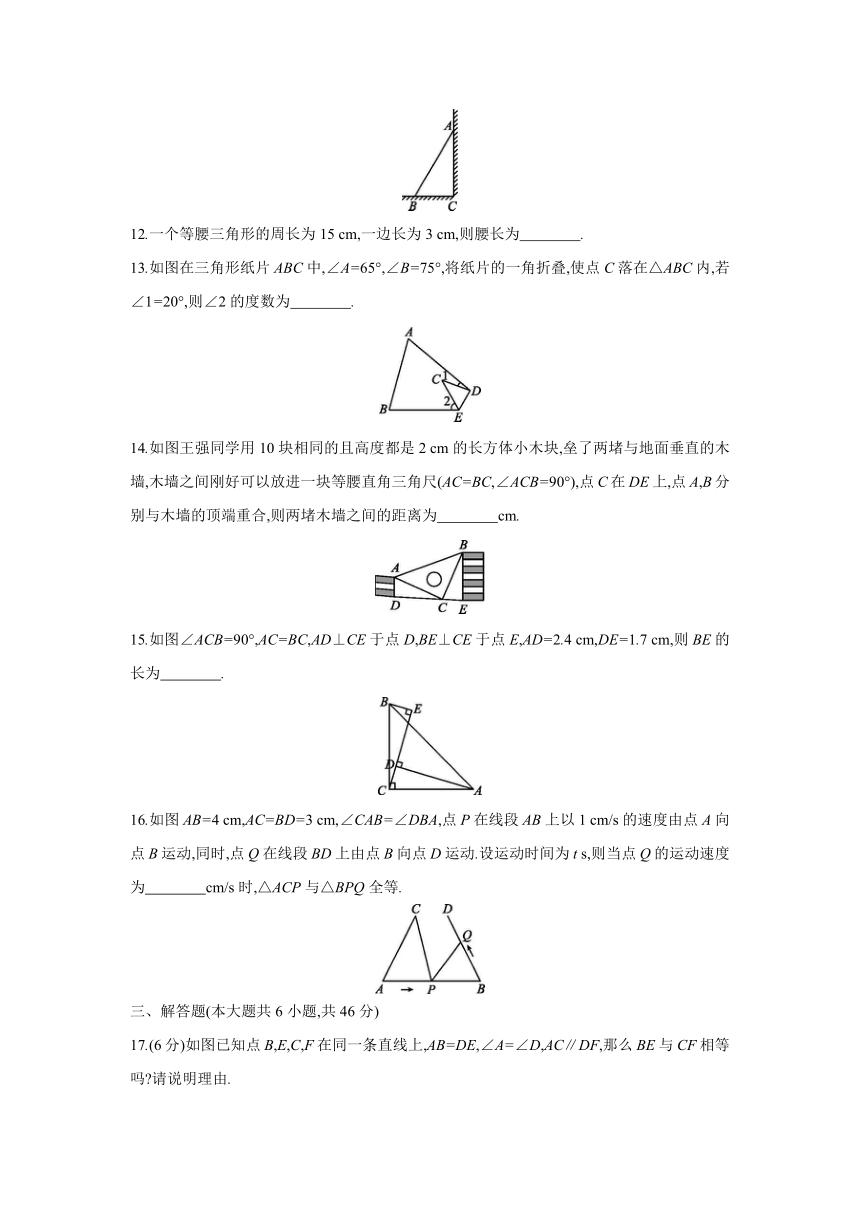
7.用直尺和圆规作一个角等于已知角,如图要证∠A'O'B'=∠AOB,需证△O'D'C'≌△ODC,依据是 ( )
A.SAS B.SSS C.AAS D.ASA
8.如图点A,D,C,E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=10,AC=7,则CD的长为 ( )
A.5.5 B.4 C.4.5 D.3
9.如是5×5的正方形网格,以格点D,E为两个顶点作位置不同的格点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多可以作出 ( )
A.2个 B.4个 C.6个 D.8个
10.如图已知△ABC≌△AEF,其中点F在BC上,AB=AE,∠B=∠E.有下列结论:①AC=AF;②∠BAF=∠B;③EF=BC;④∠BAE=∠CAF.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共6小题,每小题4分,共24分)
11.如图一架梯子斜靠在墙上,梯子与地面的夹角∠ABC=60°,则梯子与墙的夹角∠BAC= °.
12.一个等腰三角形的周长为15 cm,一边长为3 cm,则腰长为 .
13.如图在三角形纸片ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠1=20°,则∠2的度数为 .
14.如图王强同学用10块相同的且高度都是2 cm的长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一块等腰直角三角尺(AC=BC,∠ACB=90°),点C在DE上,点A,B分别与木墙的顶端重合,则两堵木墙之间的距离为 cm.
15.如图∠ACB=90°,AC=BC,AD⊥CE于点D,BE⊥CE于点E,AD=2.4 cm,DE=1.7 cm,则BE的长为 .
16.如图AB=4 cm,AC=BD=3 cm,∠CAB=∠DBA,点P在线段AB上以1 cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.设运动时间为t s,则当点Q的运动速度为 cm/s时,△ACP与△BPQ全等.
三、解答题(本大题共6小题,共46分)
17.(6分)如图已知点B,E,C,F在同一条直线上,AB=DE,∠A=∠D,AC∥DF,那么BE与CF相等吗 请说明理由.
18.(6分)如图在△ABC中,AD是高,角平分线AE,BF相交于点O,∠BAC=50°,∠C=∠BAC+20°,求∠DAC和∠BOA的度数.
19.(7分)七年级(2)班的篮球啦啦队为了在明天的比赛中给同学们加油助威,每人提前制作了一面同一规格的三角形彩旗.小贝放学回家后,发现自己的彩旗破损了一角(如①),她想用彩纸重新制作一面彩旗.
(1)请你帮助小贝,用直尺与圆规在彩纸上(如图②)作出一个与破损前完全一样的三角形(不写作法,保留作图痕迹);
(2)你作图的理由是判定三角形全等条件中的“ ”.
20.(8分)如图点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2.
(1)试说明:△ABE≌△CBD;
(2)试说明:∠1=∠3.
21.(9分)如图为了测量一幢楼高AB,在旗杆CD与楼AB之间选定一点P,测得旗杆顶C的视线PC与地面夹角∠DPC=38°,测得楼顶A的视线PA与地面夹角∠APB=52°,量得点P到楼底的距离PB与旗杆高度都等于14 m,量得旗杆与楼之间的距离DB=33 m,则楼高AB是多少米
22.(10分)如图在Rt△ABC中,∠ACB=90°,直线l过点C.
(1)当AC=BC时,如图(a),分别过点A,B作AD⊥l于点D,BE⊥l于点E.试说明:△ACD≌△CBE.
(2)当AC=8,BC=6时,如图(b),点B与点F关于直线l对称,连接BF,CF,动点M从点A出发,以每秒1个单位长度的速度沿AC边向终点C运动,同时动点N从点F出发,以每秒3个单位长度的速度沿F→C→B→C→F向终点F运动,点M,N到达相应的终点时停止运动,过点M作MD⊥l于点D,过点N作NE⊥l于点E,设运动时间为t秒.
①CM= ,当点N在F→C路径上时,CN= ;(用含t的代数式表示)
②直接写出当△MDC与△CEN全等时t的值.
答案
1.A
2.D
3.B 因为三个内角度数之比为2∶3∶4,所以三个角分别为40°,60°,80°,所以这个三角形为锐角三角形.故选B.
4.D
5.C
6.D A项,添加BC=EC,∠B=∠E可用SAS判定两个三角形全等;B项,添加BC=EC,AC=DC可用SSS判定两个三角形全等;C项,添加∠B=∠E,∠A=∠D可用ASA判定两个三角形全等;D项,添加BC=EC,∠A=∠D后是SSA,无法判定三角形全等.故选D.
7.B
8.B 因为AB∥EF,所以∠A=∠E.在△ABC和△EFD中,因为∠A=∠E,AB=EF,
∠B=∠F,所以△ABC≌△EFD(ASA),所以AC=ED=7,所以AD=AE-ED=10-7=3,
所以CD=AC-AD=7-3=4.故选B.
9.B
10.C
11.30 12.6 cm
13.60°
14.20
15.0.7 cm
16.1或1.5
17.解:BE=CF.理由如下:
因为AC∥DF,所以∠ACB=∠F.
在△ABC和△DEF中,
因为∠A=∠D,∠ACB=∠F,AB=DE,
所以△ABC≌△DEF(AAS).
所以BC=EF.
所以BC-EC=EF-EC,
即BE=CF.
18.解:因为∠BAC=50°,∠C=∠BAC+20°,
所以∠C=70°.
因为AD是△ABC的高,
所以AD⊥BC,
所以∠ADC=90°,
所以∠DAC=180°-∠C-∠ADC=20°.
因为∠BAC=50°,∠C=70°,
所以∠ABC=180°-∠BAC-∠C=60°.
因为AE,BF是△ABC的角平分线,
所以∠BAE=∠BAC=25°,∠ABF=∠ABC=30°,
所以∠BOA=180°-∠BAE-∠ABF=180°-25°-30°=125°.
19.解:(1)如图所示,△ABC即为所求作的三角形.
(2)ASA
20.解:(1)因为∠1=∠2,
所以∠1+∠CBE=∠2+∠CBE,
即∠ABE=∠CBD.
在△ABE和△CBD中,
因为AB=CB,∠ABE=∠CBD,BE=BD,
所以△ABE≌△CBD(SAS).
(2)因为△ABE≌△CBD,所以∠A=∠C.
又因为∠AFB=∠CFE,
所以∠1=∠3.
21.解:因为∠DPC=38°,∠CDP=90°,
所以∠DCP=52°,所以∠DCP=∠APB.
在△CPD和△PAB中,
因为∠CDP=∠PBA,DC=BP,∠DCP=∠BPA,
所以△CPD≌△PAB(ASA).
所以PD=AB.
因为DB=33,PB=14,
所以AB=PD=DB-PB=33-14=19(m).
故楼高AB是19 m.
22.解:(1)因为AD⊥l,BE⊥l,
所以∠ADC=∠CEB=90°,
所以∠DAC+∠ACD=90°.
因为∠ACB=90°,
所以∠ECB+∠ACD=90°,
所以∠DAC=∠ECB.
在△ACD和△CBE中,
因为∠ADC=∠CEB,∠DAC=∠ECB,AC=CB,
所以△ACD≌△CBE(AAS).
(2)①8-t 6-3t
②由题意可知∠BCE=∠NCE.
因为MD⊥l,NE⊥l,所以∠MDC=∠CEN=90°,所以∠MCD+∠CMD=90°.
因为∠ACB=90°,所以∠MCD+∠BCE=90°,
所以∠CMD=∠BCE,所以∠NCE=∠CMD,
故当CM=CN时,△MDC与△NEC全等.
当点N在F→C路径上时,8-t=6-3t,
解得t=-1(不合题意);
当点N在C→B路径上时,CN=3t-6,
所以8-t=3t-6,
解得t=3.5;
当点N在B→C路径上时,CN=18-3t,
所以8-t=18-3t,
解得t=5;
当点N在C→F路径上时,CN=3t-18,
所以8-t=3t-18,
解得t=6.5.
综上所述,当t的值为3.5或5或6.5时,△MDC与△CEN全等.
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列图形中与已知图形()全等的是 ( )
2.下列图形中,AD是△ABC的高的是 ( )
3.若一个三角形三个内角的度数之比为2∶3∶4,则这个三角形是 ( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
4.已知三角形的三条边长分别为4,a,8,那么该三角形的周长C的取值范围是 ( )
A.4
A.2 B.3 C.4 D.5
6.如图在△ABC和△DEC中,AB=DE.若添加条件后使得△ABC≌△DEC,则在下列条件中,不能添加的是 ( )
A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.∠B=∠E,∠A=∠D D.BC=EC,∠A=∠D
7.用直尺和圆规作一个角等于已知角,如图要证∠A'O'B'=∠AOB,需证△O'D'C'≌△ODC,依据是 ( )
A.SAS B.SSS C.AAS D.ASA
8.如图点A,D,C,E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=10,AC=7,则CD的长为 ( )
A.5.5 B.4 C.4.5 D.3
9.如是5×5的正方形网格,以格点D,E为两个顶点作位置不同的格点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多可以作出 ( )
A.2个 B.4个 C.6个 D.8个
10.如图已知△ABC≌△AEF,其中点F在BC上,AB=AE,∠B=∠E.有下列结论:①AC=AF;②∠BAF=∠B;③EF=BC;④∠BAE=∠CAF.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共6小题,每小题4分,共24分)
11.如图一架梯子斜靠在墙上,梯子与地面的夹角∠ABC=60°,则梯子与墙的夹角∠BAC= °.
12.一个等腰三角形的周长为15 cm,一边长为3 cm,则腰长为 .
13.如图在三角形纸片ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠1=20°,则∠2的度数为 .
14.如图王强同学用10块相同的且高度都是2 cm的长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一块等腰直角三角尺(AC=BC,∠ACB=90°),点C在DE上,点A,B分别与木墙的顶端重合,则两堵木墙之间的距离为 cm.
15.如图∠ACB=90°,AC=BC,AD⊥CE于点D,BE⊥CE于点E,AD=2.4 cm,DE=1.7 cm,则BE的长为 .
16.如图AB=4 cm,AC=BD=3 cm,∠CAB=∠DBA,点P在线段AB上以1 cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.设运动时间为t s,则当点Q的运动速度为 cm/s时,△ACP与△BPQ全等.
三、解答题(本大题共6小题,共46分)
17.(6分)如图已知点B,E,C,F在同一条直线上,AB=DE,∠A=∠D,AC∥DF,那么BE与CF相等吗 请说明理由.
18.(6分)如图在△ABC中,AD是高,角平分线AE,BF相交于点O,∠BAC=50°,∠C=∠BAC+20°,求∠DAC和∠BOA的度数.
19.(7分)七年级(2)班的篮球啦啦队为了在明天的比赛中给同学们加油助威,每人提前制作了一面同一规格的三角形彩旗.小贝放学回家后,发现自己的彩旗破损了一角(如①),她想用彩纸重新制作一面彩旗.
(1)请你帮助小贝,用直尺与圆规在彩纸上(如图②)作出一个与破损前完全一样的三角形(不写作法,保留作图痕迹);
(2)你作图的理由是判定三角形全等条件中的“ ”.
20.(8分)如图点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2.
(1)试说明:△ABE≌△CBD;
(2)试说明:∠1=∠3.
21.(9分)如图为了测量一幢楼高AB,在旗杆CD与楼AB之间选定一点P,测得旗杆顶C的视线PC与地面夹角∠DPC=38°,测得楼顶A的视线PA与地面夹角∠APB=52°,量得点P到楼底的距离PB与旗杆高度都等于14 m,量得旗杆与楼之间的距离DB=33 m,则楼高AB是多少米
22.(10分)如图在Rt△ABC中,∠ACB=90°,直线l过点C.
(1)当AC=BC时,如图(a),分别过点A,B作AD⊥l于点D,BE⊥l于点E.试说明:△ACD≌△CBE.
(2)当AC=8,BC=6时,如图(b),点B与点F关于直线l对称,连接BF,CF,动点M从点A出发,以每秒1个单位长度的速度沿AC边向终点C运动,同时动点N从点F出发,以每秒3个单位长度的速度沿F→C→B→C→F向终点F运动,点M,N到达相应的终点时停止运动,过点M作MD⊥l于点D,过点N作NE⊥l于点E,设运动时间为t秒.
①CM= ,当点N在F→C路径上时,CN= ;(用含t的代数式表示)
②直接写出当△MDC与△CEN全等时t的值.
答案
1.A
2.D
3.B 因为三个内角度数之比为2∶3∶4,所以三个角分别为40°,60°,80°,所以这个三角形为锐角三角形.故选B.
4.D
5.C
6.D A项,添加BC=EC,∠B=∠E可用SAS判定两个三角形全等;B项,添加BC=EC,AC=DC可用SSS判定两个三角形全等;C项,添加∠B=∠E,∠A=∠D可用ASA判定两个三角形全等;D项,添加BC=EC,∠A=∠D后是SSA,无法判定三角形全等.故选D.
7.B
8.B 因为AB∥EF,所以∠A=∠E.在△ABC和△EFD中,因为∠A=∠E,AB=EF,
∠B=∠F,所以△ABC≌△EFD(ASA),所以AC=ED=7,所以AD=AE-ED=10-7=3,
所以CD=AC-AD=7-3=4.故选B.
9.B
10.C
11.30 12.6 cm
13.60°
14.20
15.0.7 cm
16.1或1.5
17.解:BE=CF.理由如下:
因为AC∥DF,所以∠ACB=∠F.
在△ABC和△DEF中,
因为∠A=∠D,∠ACB=∠F,AB=DE,
所以△ABC≌△DEF(AAS).
所以BC=EF.
所以BC-EC=EF-EC,
即BE=CF.
18.解:因为∠BAC=50°,∠C=∠BAC+20°,
所以∠C=70°.
因为AD是△ABC的高,
所以AD⊥BC,
所以∠ADC=90°,
所以∠DAC=180°-∠C-∠ADC=20°.
因为∠BAC=50°,∠C=70°,
所以∠ABC=180°-∠BAC-∠C=60°.
因为AE,BF是△ABC的角平分线,
所以∠BAE=∠BAC=25°,∠ABF=∠ABC=30°,
所以∠BOA=180°-∠BAE-∠ABF=180°-25°-30°=125°.
19.解:(1)如图所示,△ABC即为所求作的三角形.
(2)ASA
20.解:(1)因为∠1=∠2,
所以∠1+∠CBE=∠2+∠CBE,
即∠ABE=∠CBD.
在△ABE和△CBD中,
因为AB=CB,∠ABE=∠CBD,BE=BD,
所以△ABE≌△CBD(SAS).
(2)因为△ABE≌△CBD,所以∠A=∠C.
又因为∠AFB=∠CFE,
所以∠1=∠3.
21.解:因为∠DPC=38°,∠CDP=90°,
所以∠DCP=52°,所以∠DCP=∠APB.
在△CPD和△PAB中,
因为∠CDP=∠PBA,DC=BP,∠DCP=∠BPA,
所以△CPD≌△PAB(ASA).
所以PD=AB.
因为DB=33,PB=14,
所以AB=PD=DB-PB=33-14=19(m).
故楼高AB是19 m.
22.解:(1)因为AD⊥l,BE⊥l,
所以∠ADC=∠CEB=90°,
所以∠DAC+∠ACD=90°.
因为∠ACB=90°,
所以∠ECB+∠ACD=90°,
所以∠DAC=∠ECB.
在△ACD和△CBE中,
因为∠ADC=∠CEB,∠DAC=∠ECB,AC=CB,
所以△ACD≌△CBE(AAS).
(2)①8-t 6-3t
②由题意可知∠BCE=∠NCE.
因为MD⊥l,NE⊥l,所以∠MDC=∠CEN=90°,所以∠MCD+∠CMD=90°.
因为∠ACB=90°,所以∠MCD+∠BCE=90°,
所以∠CMD=∠BCE,所以∠NCE=∠CMD,
故当CM=CN时,△MDC与△NEC全等.
当点N在F→C路径上时,8-t=6-3t,
解得t=-1(不合题意);
当点N在C→B路径上时,CN=3t-6,
所以8-t=3t-6,
解得t=3.5;
当点N在B→C路径上时,CN=18-3t,
所以8-t=18-3t,
解得t=5;
当点N在C→F路径上时,CN=3t-18,
所以8-t=3t-18,
解得t=6.5.
综上所述,当t的值为3.5或5或6.5时,△MDC与△CEN全等.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
