2022--2023学年青岛版七年级数学上册1.3.1线段、射线和直线 课件(共26张PPT)
文档属性
| 名称 | 2022--2023学年青岛版七年级数学上册1.3.1线段、射线和直线 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 875.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-16 17:20:52 | ||
图片预览






文档简介
(共26张PPT)
温故知新
1、 、 、 、 以及它们的组合都是几何图形。
2、点、线 、面、体之间的联系
是 。
3、正方体的平面展开图共有 种情况?下列平面展开图能否组成立方体? 能组成立方体 的请说出相对的两个面。
面
体
面动成体
线动成面
点动成线
11
(1)
(2)
1
3
4
6
5
2
3
4
6
5
2
1
点
线
我来猜:
有始有终——
打一线的名称。
有始无终——
打一线的名称。
无始无终——
打一线的名称。
1.3 线段、射线和直线(1)
学习目标
1、了解线段、射线和直线的概念,能识别线段、射线和直线,能说出线段、射线、直线的区别与联系。
2、按要求画出线段、射线和直线,并能用字母正确表示这些图形,感受符号在描述图形中的作用。
▲活动一
线段、射线和直线的区别与联系。
观察上面的图片,并回答:
图(1)中同学们没用力拔河时,绳子是直的还是曲的?
图(2)中同学们用力拔河时,绳子是直的还是曲的?
(1)
(2)
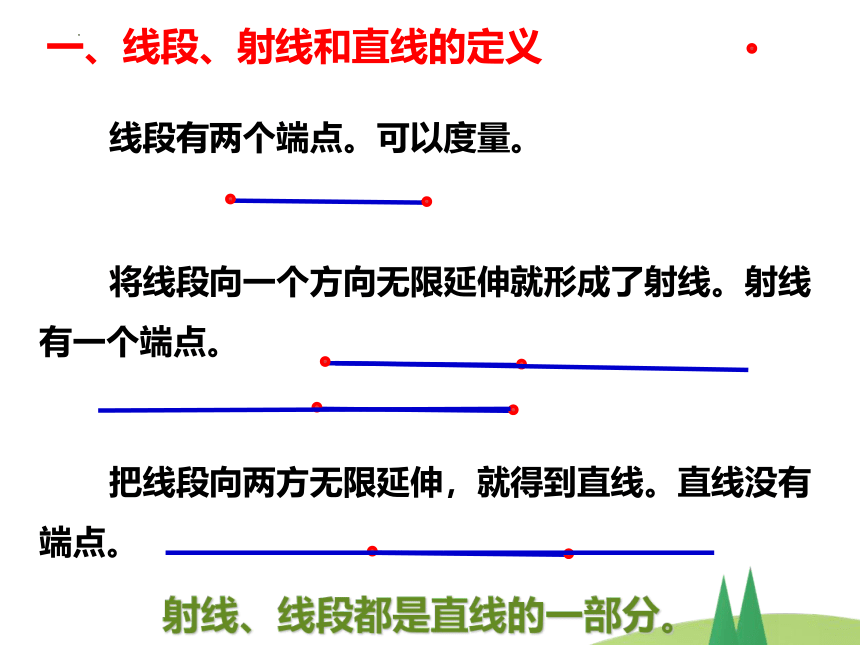
线段有两个端点。可以度量。
将线段向一个方向无限延伸就形成了射线。射线 有一个端点。
把线段向两方无限延伸,就得到直线。直线没有
端点。
射线、线段都是直线的一部分。
一、线段、射线和直线的定义
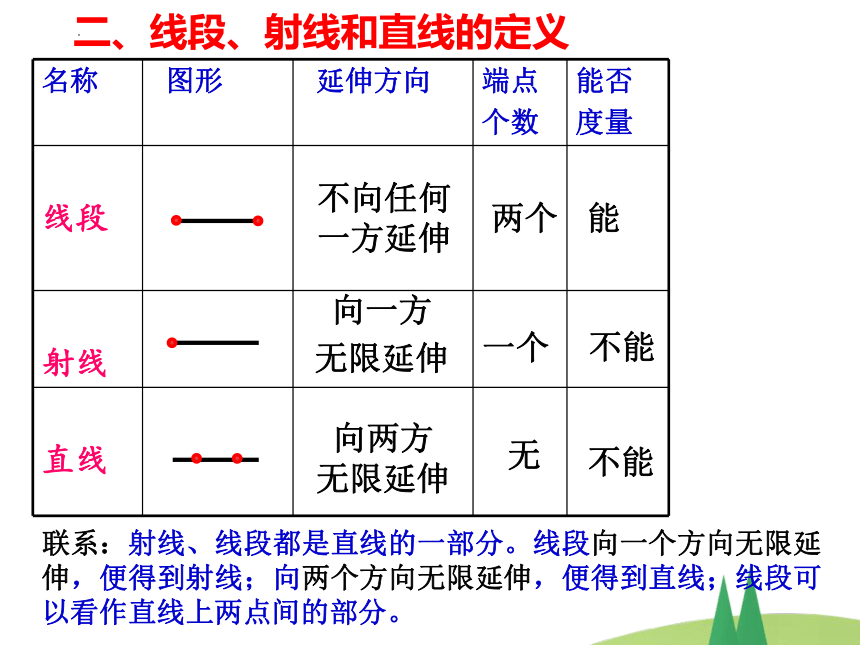
名称 图形 延伸方向 端点 个数 能否
度量
线段
射线
直线
不向任何
一方延伸
向一方
无限延伸
向两方
无限延伸
两个
一个
无
能
不能
不能
联系:射线、线段都是直线的一部分。线段向一个方向无限延伸,便得到射线;向两个方向无限延伸,便得到直线;线段可以看作直线上两点间的部分。
二、线段、射线和直线的定义
▲活动二
线段、射线和直线的表示方法。
A
B
表示方法:
点用一个大写字母表示。
一、点的表示
A
B
表示:线段 AB(或线段BA)
a
表示:线段 a
1. 端点的两个大写字母表示;
2. 一个小写字母表示.
线段有两种表示方法:
二、线段、射线和直线的表示
字母没有顺序
O
表示:射线 OP/射线OQ
射线 a
1. 端点和射线上的另一点表示,
其中,表示端点的字母必须写在前面.
2. 一个小写字母表示.
射线的表示方法:
P
a
字母有顺序
Q
A
B
表示:直线 AB(或直线AB)
l
表示:直线 l
1.两个大写字母表示;
2.一个小写字母来表示.
直线有两种表示方法:
字母没有顺序
小试牛刀
1、射线BA和射线AB是同一条射线吗 为什么 你可以画图说明吗?
2.具备什么条件的两条射线是同一条射线
同一端点
同一延伸方向
A
B
3、(多选)下列叙述正确的是( )
A.直线MN和直线NM是同一条直线
B.射线PM和射线MN是同一条射线
C.射线PM和射线PN是同一条射线
D.线段MN和线段NM是同一条线段
P
M
N
典例分析—确定线段、射线和直线
如图所示A,B,C是直线 l 上的3个点.
(1)图中共有几条线段?这些线段怎样表示?
(2)图中共有几条射线?以点B为端点的射线如何表示?
(3)直线L还可以怎样表示?
B
A
C
l
1.看图填空:
(1)能用字母表示的直线有_______条,分别是 .
。
(2)能用字母表示的线段有_______条
(3)图中共有___条射线,能用字母表示的有 条,在直线BC上的有 条。
跟踪训练
A
B
C
D
3
直线AB
直线BC,直线AD
6
14
8
6
A
B
C
D
2、根据几何语言画出下列图形?
(1)连接线段AB
(2)画出射线BC
(3)画出直线AC
(4)连接AD并延长
▲活动三
利用线段数量模型解决实际问题。
实际运用
引例、如图所示,线段上AB上有两个点C,D,请计算出图中共有多少线段?如果再添两个点E,F呢?
A
B
C
D
E
F
如果线段上有n个点(包括线段的两个端点),那么该线段上共有多少条线段?
冠县和聊城之间途中有烟庄、贾镇、闫营、堂邑、道口铺五个站点,问冠县和聊城之间共有几种票价?
实际运用—车票问题
聊城
冠县
烟庄
贾镇
闫营
堂邑
道口铺
七年级八班54名同学在某次活动中,若每两个人握手一次,那么共握手多少次?
实际运用—握手问题
若有9位同学参加学校的演讲比赛,每两位同学之间都要进行一场比赛,一共要进行多少场比赛?
实际运用—比赛问题
回顾总结
我的收获?
1.线段、射线和直线区别和联系
2.线段、射线和直线的表示方法
3.从图形中准确找出线段与射线的条数
4.线段数量模型
达标测试
1.课本15页练习
2.课本17页习题1、2
作业
1
2
3
4
5
7
6
8
9
2
1
3
4
5
7
6
8
9
图1-24
在图1-24中,请你将邻边上相同数表示的点用线段分别连接起来,看看会得到一个什么样的图形。
智趣园—以直“诱”曲
1
2
3
4
5
7
6
8
9
2
1
3
4
5
7
6
8
9
图1-24
智趣园—以直“诱”曲
在一定条件下,曲直不太分明,曲直可以相互转化。在数学中,常常借助直线研究曲线。离开了“直”就难以研究“曲”
温故知新
1、 、 、 、 以及它们的组合都是几何图形。
2、点、线 、面、体之间的联系
是 。
3、正方体的平面展开图共有 种情况?下列平面展开图能否组成立方体? 能组成立方体 的请说出相对的两个面。
面
体
面动成体
线动成面
点动成线
11
(1)
(2)
1
3
4
6
5
2
3
4
6
5
2
1
点
线
我来猜:
有始有终——
打一线的名称。
有始无终——
打一线的名称。
无始无终——
打一线的名称。
1.3 线段、射线和直线(1)
学习目标
1、了解线段、射线和直线的概念,能识别线段、射线和直线,能说出线段、射线、直线的区别与联系。
2、按要求画出线段、射线和直线,并能用字母正确表示这些图形,感受符号在描述图形中的作用。
▲活动一
线段、射线和直线的区别与联系。
观察上面的图片,并回答:
图(1)中同学们没用力拔河时,绳子是直的还是曲的?
图(2)中同学们用力拔河时,绳子是直的还是曲的?
(1)
(2)
线段有两个端点。可以度量。
将线段向一个方向无限延伸就形成了射线。射线 有一个端点。
把线段向两方无限延伸,就得到直线。直线没有
端点。
射线、线段都是直线的一部分。
一、线段、射线和直线的定义
名称 图形 延伸方向 端点 个数 能否
度量
线段
射线
直线
不向任何
一方延伸
向一方
无限延伸
向两方
无限延伸
两个
一个
无
能
不能
不能
联系:射线、线段都是直线的一部分。线段向一个方向无限延伸,便得到射线;向两个方向无限延伸,便得到直线;线段可以看作直线上两点间的部分。
二、线段、射线和直线的定义
▲活动二
线段、射线和直线的表示方法。
A
B
表示方法:
点用一个大写字母表示。
一、点的表示
A
B
表示:线段 AB(或线段BA)
a
表示:线段 a
1. 端点的两个大写字母表示;
2. 一个小写字母表示.
线段有两种表示方法:
二、线段、射线和直线的表示
字母没有顺序
O
表示:射线 OP/射线OQ
射线 a
1. 端点和射线上的另一点表示,
其中,表示端点的字母必须写在前面.
2. 一个小写字母表示.
射线的表示方法:
P
a
字母有顺序
Q
A
B
表示:直线 AB(或直线AB)
l
表示:直线 l
1.两个大写字母表示;
2.一个小写字母来表示.
直线有两种表示方法:
字母没有顺序
小试牛刀
1、射线BA和射线AB是同一条射线吗 为什么 你可以画图说明吗?
2.具备什么条件的两条射线是同一条射线
同一端点
同一延伸方向
A
B
3、(多选)下列叙述正确的是( )
A.直线MN和直线NM是同一条直线
B.射线PM和射线MN是同一条射线
C.射线PM和射线PN是同一条射线
D.线段MN和线段NM是同一条线段
P
M
N
典例分析—确定线段、射线和直线
如图所示A,B,C是直线 l 上的3个点.
(1)图中共有几条线段?这些线段怎样表示?
(2)图中共有几条射线?以点B为端点的射线如何表示?
(3)直线L还可以怎样表示?
B
A
C
l
1.看图填空:
(1)能用字母表示的直线有_______条,分别是 .
。
(2)能用字母表示的线段有_______条
(3)图中共有___条射线,能用字母表示的有 条,在直线BC上的有 条。
跟踪训练
A
B
C
D
3
直线AB
直线BC,直线AD
6
14
8
6
A
B
C
D
2、根据几何语言画出下列图形?
(1)连接线段AB
(2)画出射线BC
(3)画出直线AC
(4)连接AD并延长
▲活动三
利用线段数量模型解决实际问题。
实际运用
引例、如图所示,线段上AB上有两个点C,D,请计算出图中共有多少线段?如果再添两个点E,F呢?
A
B
C
D
E
F
如果线段上有n个点(包括线段的两个端点),那么该线段上共有多少条线段?
冠县和聊城之间途中有烟庄、贾镇、闫营、堂邑、道口铺五个站点,问冠县和聊城之间共有几种票价?
实际运用—车票问题
聊城
冠县
烟庄
贾镇
闫营
堂邑
道口铺
七年级八班54名同学在某次活动中,若每两个人握手一次,那么共握手多少次?
实际运用—握手问题
若有9位同学参加学校的演讲比赛,每两位同学之间都要进行一场比赛,一共要进行多少场比赛?
实际运用—比赛问题
回顾总结
我的收获?
1.线段、射线和直线区别和联系
2.线段、射线和直线的表示方法
3.从图形中准确找出线段与射线的条数
4.线段数量模型
达标测试
1.课本15页练习
2.课本17页习题1、2
作业
1
2
3
4
5
7
6
8
9
2
1
3
4
5
7
6
8
9
图1-24
在图1-24中,请你将邻边上相同数表示的点用线段分别连接起来,看看会得到一个什么样的图形。
智趣园—以直“诱”曲
1
2
3
4
5
7
6
8
9
2
1
3
4
5
7
6
8
9
图1-24
智趣园—以直“诱”曲
在一定条件下,曲直不太分明,曲直可以相互转化。在数学中,常常借助直线研究曲线。离开了“直”就难以研究“曲”
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
