2022—2023学年人教版数学七年级上册4.4制作长方体形状的设计包装纸盒 课件(共23张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学七年级上册4.4制作长方体形状的设计包装纸盒 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-16 17:23:08 | ||
图片预览




文档简介
(共23张PPT)
几何图形初步
初中数学/ 人教版 / 七年级上册
1. 课前预热
2. 导入新课
3. 典例解析
4. 当堂小测
5. 课堂小结
6. 课后练习
目 录
4.4制作长方体形状的设计包装纸盒
课前预热
教学重点:掌握包装纸盒的的一般方法,能够独立制作出相关包装盒。
教学难点:通过问题解决进一步理解立体图形和相应平面图形之间的转化。
教学目标:掌握包装纸盒的的一般方法,能够独立制作出相关包装盒,通过问题解决进一步理解立体图形和相应平面图形之间的转化。
课前预热
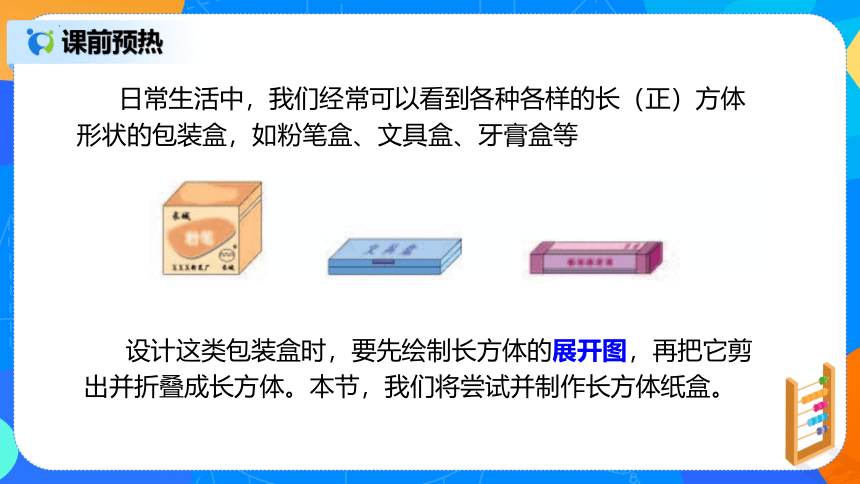
日常生活中,我们经常可以看到各种各样的长(正)方体形状的包装盒,如粉笔盒、文具盒、牙膏盒等
设计这类包装盒时,要先绘制长方体的展开图,再把它剪出并折叠成长方体。本节,我们将尝试并制作长方体纸盒。
导入新课
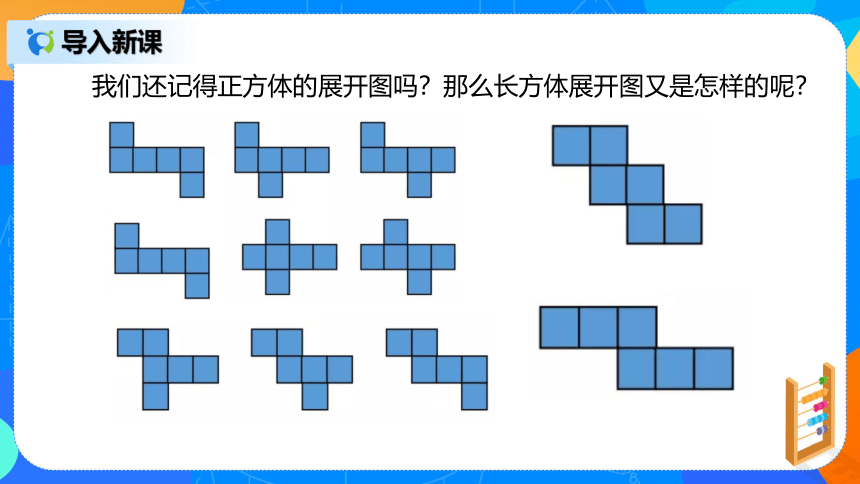
我们还记得正方体的展开图吗?那么长方体展开图又是怎样的呢?
导入新课
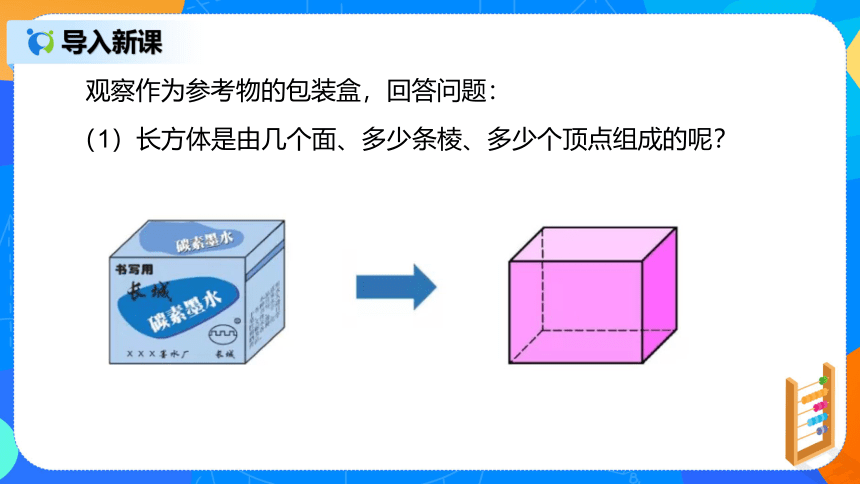
观察作为参考物的包装盒,回答问题:
(1)长方体是由几个面、多少条棱、多少个顶点组成的呢?
导入新课
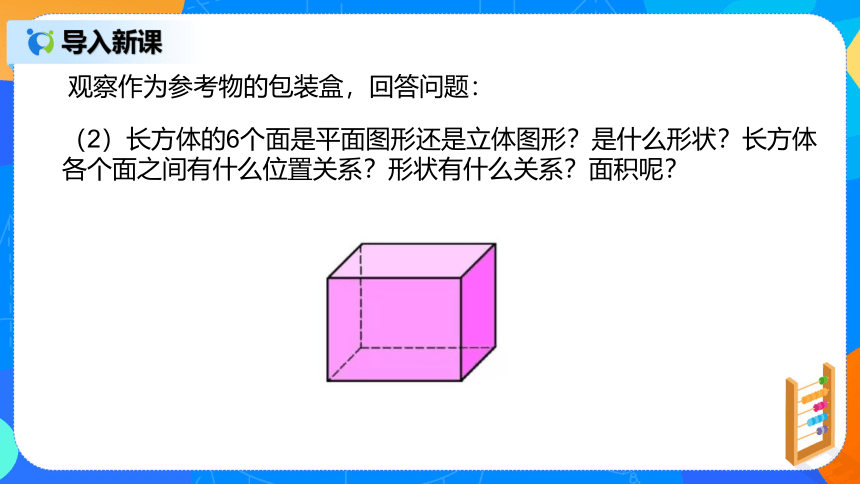
观察作为参考物的包装盒,回答问题:
(2)长方体的6个面是平面图形还是立体图形?是什么形状?长方体
各个面之间有什么位置关系?形状有什么关系?面积呢?
导入新课
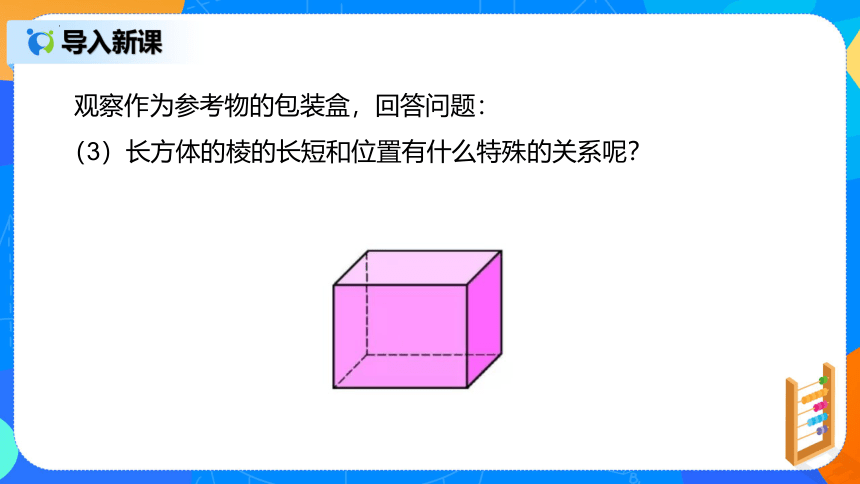
观察作为参考物的包装盒,回答问题:
(3)长方体的棱的长短和位置有什么特殊的关系呢?
导入新课
拆开观察长方体包装盒的展开图。
(1)将每一组的纸制长方体沿棱剪开,展开成一个完整的平面展开图,需要剪开多少条棱?
导入新课
拆开观察长方体包装盒的展开图。
请各小组到讲台前展示各自的图形。
·····
导入新课
拆开观察长方体包装盒的展开图。
(2)所得的平面展开图是什么样的?找出对应长方体各面、棱的相
应部分,找出其中的关系。
导入新课
还原表面展开图包装盒。
观察它是如何折叠粘到一起的,重点观察一下它是如何折叠的。
典例分析
例1.将图1的正四角锥 ABCDE 沿着其中的四个边剪开后,形成的展开图为图2.判断下列哪一个选项中的四个边可为此四个边?( )
A.AC、AD、BC、DE B.AB、BE、DE、CD
C.AC、BC、AE、DE D.AC、AD、AE、BC
立体图形与平面图形的相互转化
A
典例分析
例2.某商品的外包装箱是长方体,其展开图的面积为430平方分米,其中BC=5分米,EF=10分米,则AB的长度为_______分米。
实际应用
11
解:分析此商品展开图各个部分都是矩形
2×(5AB+10AB+5×10)=430
AB=11
典例分析
例3.如图为一无盖长方体盒子的展开图(重叠部分不计),可知该无盖长方体的容积为( )
A.4 B.6 C.8 D.12
实际应用
C
当堂小测
1.在4个图形中,只有一个是由如图所示的纸板折叠而成,请你选出正确的一个( )
2.下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方形包装盒的是( )
A
A. B. C. D.
D
当堂小测
3.如图是一个长方体的表面展开图,每个面上都标注了字母和数据,请根据要求回答:(1)如果A面在长方体的底部,那么_____面会在上面;(2)求这个长方体表面积和体积。
解:(1)F
(2)由图知
表面积为:2×(1×3+1×2+2×3)=22(平方米)
体积是:1×2×3=6(立方米)
F
课堂小结
制作立体图形:
课堂小结
常见几何图的展开图:
长方体
四棱锥
圆锥
三棱柱
三棱锥
三棱柱
正方体
圆柱
课后练习
1.已知 O 为圆锥的顶点,M 为圆锥底面圆上一点,点 P 在 OM 上.一只蜗牛从 P 点出发,绕圆锥侧面爬行,回到 P 点时,所爬过的最短路线的痕迹如图所示.若沿 OM 将圆锥侧面剪开并展平,所得侧面展开图(如图)是( )
2. 将正方体的表面沿某些棱剪开,展成如图所示的平面图形,则原正方体中与“创”字所在的面相对的面上标的字是( )
A.庆 B.力 C.大 D.魅
A
D
课后练习
3.如图,一个长方体的表面展开图中四边形ABCD是正方形(正方形的四个角都是直角、四条边都相等),则根据图中数据可得原长方体的体积是多少cm ?
解:因为四边形ABCD是正方形。
所以AB=AE=5cm
所以立方体的高为:(7-5)÷2=1(cm)
所以EF=5-1=4(cm)
所以原长方体的体积是:5×4×1=20(cm )
谢谢观看
几何图形初步
初中数学/ 人教版 / 七年级上册
1. 课前预热
2. 导入新课
3. 典例解析
4. 当堂小测
5. 课堂小结
6. 课后练习
目 录
4.4制作长方体形状的设计包装纸盒
课前预热
教学重点:掌握包装纸盒的的一般方法,能够独立制作出相关包装盒。
教学难点:通过问题解决进一步理解立体图形和相应平面图形之间的转化。
教学目标:掌握包装纸盒的的一般方法,能够独立制作出相关包装盒,通过问题解决进一步理解立体图形和相应平面图形之间的转化。
课前预热
日常生活中,我们经常可以看到各种各样的长(正)方体形状的包装盒,如粉笔盒、文具盒、牙膏盒等
设计这类包装盒时,要先绘制长方体的展开图,再把它剪出并折叠成长方体。本节,我们将尝试并制作长方体纸盒。
导入新课
我们还记得正方体的展开图吗?那么长方体展开图又是怎样的呢?
导入新课
观察作为参考物的包装盒,回答问题:
(1)长方体是由几个面、多少条棱、多少个顶点组成的呢?
导入新课
观察作为参考物的包装盒,回答问题:
(2)长方体的6个面是平面图形还是立体图形?是什么形状?长方体
各个面之间有什么位置关系?形状有什么关系?面积呢?
导入新课
观察作为参考物的包装盒,回答问题:
(3)长方体的棱的长短和位置有什么特殊的关系呢?
导入新课
拆开观察长方体包装盒的展开图。
(1)将每一组的纸制长方体沿棱剪开,展开成一个完整的平面展开图,需要剪开多少条棱?
导入新课
拆开观察长方体包装盒的展开图。
请各小组到讲台前展示各自的图形。
·····
导入新课
拆开观察长方体包装盒的展开图。
(2)所得的平面展开图是什么样的?找出对应长方体各面、棱的相
应部分,找出其中的关系。
导入新课
还原表面展开图包装盒。
观察它是如何折叠粘到一起的,重点观察一下它是如何折叠的。
典例分析
例1.将图1的正四角锥 ABCDE 沿着其中的四个边剪开后,形成的展开图为图2.判断下列哪一个选项中的四个边可为此四个边?( )
A.AC、AD、BC、DE B.AB、BE、DE、CD
C.AC、BC、AE、DE D.AC、AD、AE、BC
立体图形与平面图形的相互转化
A
典例分析
例2.某商品的外包装箱是长方体,其展开图的面积为430平方分米,其中BC=5分米,EF=10分米,则AB的长度为_______分米。
实际应用
11
解:分析此商品展开图各个部分都是矩形
2×(5AB+10AB+5×10)=430
AB=11
典例分析
例3.如图为一无盖长方体盒子的展开图(重叠部分不计),可知该无盖长方体的容积为( )
A.4 B.6 C.8 D.12
实际应用
C
当堂小测
1.在4个图形中,只有一个是由如图所示的纸板折叠而成,请你选出正确的一个( )
2.下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方形包装盒的是( )
A
A. B. C. D.
D
当堂小测
3.如图是一个长方体的表面展开图,每个面上都标注了字母和数据,请根据要求回答:(1)如果A面在长方体的底部,那么_____面会在上面;(2)求这个长方体表面积和体积。
解:(1)F
(2)由图知
表面积为:2×(1×3+1×2+2×3)=22(平方米)
体积是:1×2×3=6(立方米)
F
课堂小结
制作立体图形:
课堂小结
常见几何图的展开图:
长方体
四棱锥
圆锥
三棱柱
三棱锥
三棱柱
正方体
圆柱
课后练习
1.已知 O 为圆锥的顶点,M 为圆锥底面圆上一点,点 P 在 OM 上.一只蜗牛从 P 点出发,绕圆锥侧面爬行,回到 P 点时,所爬过的最短路线的痕迹如图所示.若沿 OM 将圆锥侧面剪开并展平,所得侧面展开图(如图)是( )
2. 将正方体的表面沿某些棱剪开,展成如图所示的平面图形,则原正方体中与“创”字所在的面相对的面上标的字是( )
A.庆 B.力 C.大 D.魅
A
D
课后练习
3.如图,一个长方体的表面展开图中四边形ABCD是正方形(正方形的四个角都是直角、四条边都相等),则根据图中数据可得原长方体的体积是多少cm ?
解:因为四边形ABCD是正方形。
所以AB=AE=5cm
所以立方体的高为:(7-5)÷2=1(cm)
所以EF=5-1=4(cm)
所以原长方体的体积是:5×4×1=20(cm )
谢谢观看
