数学人教A版(2019)必修第一册4.3.2对数的运算 课件(共17张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.3.2对数的运算 课件(共17张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-14 07:11:01 | ||
图片预览





文档简介
(共17张PPT)
对数的运算
新课程标准 核心素养
1.掌握对数的运算性质; 数学运算
2.能用换底公式将一般对数转化成自然对数或常用对数; 数学运算
3.能用对数的运算性质和换底公式进行一些简单的化简和证明 逻辑推理
知识点1
对数的运算性质
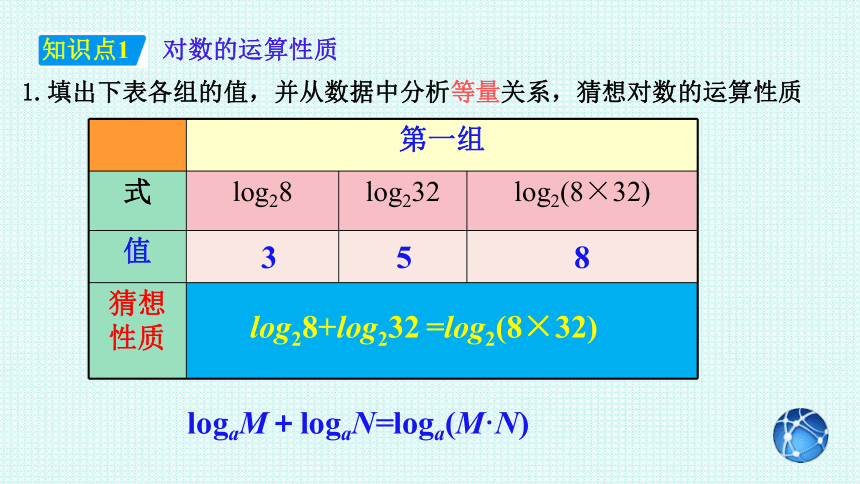
1.填出下表各组的值,并从数据中分析等量关系,猜想对数的运算性质
第一组
式 log28 log232 log2(8×32)
值
猜想性质
3
5
8
log28+log232 =log2(8×32)
logaM+logaN=loga(M·N)
第二组
式 lg1000 lg100 000
值
猜想性质
3
5
-2
lg1000-lg100 000=
lg
3
10
5
10
logaM-logaN=loga
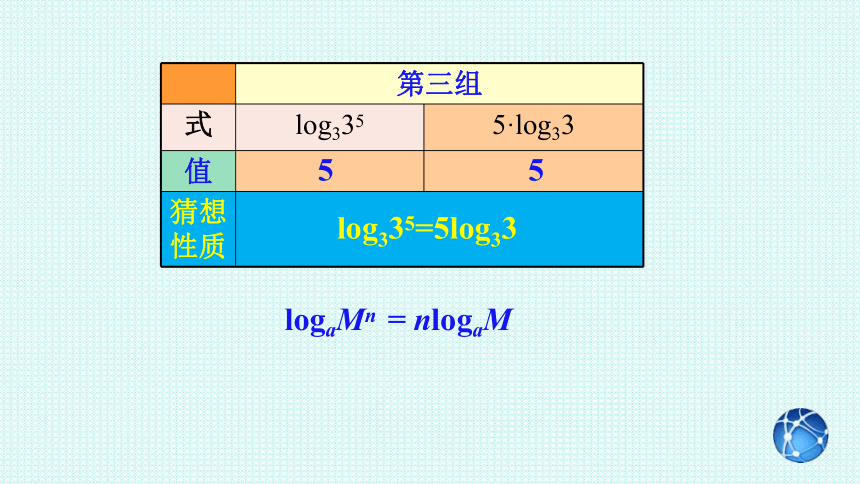
第三组
式 log335 5·log33
值
猜想性质
5
5
log335=5log33
logaMn = nlogaM
设logaM=m,logaN=n,则am=M,an=N,
(1). loga(M·N)= logaM+logaN
∴MN=am·an=am+n,
∴loga(MN)=m+n=logaM+logaN.
(2). loga =logaM-logaN
积对数等于对数之和.
商对数等于对数之差.
设logaM=p,logaN=q, M= , N=
a
p
a
q
a
p-q
M
N
=
loga =logaM-logaN
(3). logaMn = nlogaM
n次幂的对数等于n倍的对数.
设logaM=p,则 M= , Mn=
a
p
a
np
logaMn =np
logaMn = nlogaM
※ 对数运算公式几个注意点:
1) 简易语言表达:“积的对数=对数的和”,………;
2) 真数的取值必须是(0,+∞);
3) 有时公式可以可逆;
4)loga(M·N)≠ logaM·logaN
loga(M±N)≠ logaM±logaN
5)logaMn ≠( logaM )n
解:原式=log247 +log225
=7log24 +5log22
=7log222+5
=19
解:原式= lg100
= lg102
= lg10
=
1
5
1
5
2
5
2
5
解:原式=lg2+lg7-2lg7+2lg3+lg7-lg2-2lg3
=0
解:原式=2lg5+2lg2+lg5(2lg2+lg5)+(lg2)2
=2(lg5+lg2)+2lg5·lg2+(lg5)2+(lg2)2
=2+(lg2+lg5)2
=3.
知识点2
换底公式
想一想
log25
log23
=x
设 ,则log25=xlog23=log23x ,3x=5 ,x=log35
log25
log23
=
log35
1
例2.已知log189=a,18b=5,求log3645.
解 方法一 ∵log189=a,18b=5,∴log185=b,
( )
( )
解 方法二 ∵log189=a,18b=5,∴log185=b,
( )
( )
方法三 ∵log189=a,18b=5,∴lg 9=alg 18,lg 5=blg 18,
在利用换底公式进行化简求值时,一般情况是根据题中所给的对数式的具体特点选择恰当的底数进行换底,如果所给的对数式中的底数和真数互不相同,我们可以选择以10为底数进行换底.
跟踪训练 已知log23=a,log37=b,用a,b表示log4256.
又∵log37=b,
题型一
对数运算性质的应用
题型一
对数换底公式的应用
2
x
=m
x=log2m
1
x
=logm2
5
y
=m
y=log5m
1
y
=logm5
1
x
1
y
+ =2
logm2+logm5=logm10=2
对数的运算
新课程标准 核心素养
1.掌握对数的运算性质; 数学运算
2.能用换底公式将一般对数转化成自然对数或常用对数; 数学运算
3.能用对数的运算性质和换底公式进行一些简单的化简和证明 逻辑推理
知识点1
对数的运算性质
1.填出下表各组的值,并从数据中分析等量关系,猜想对数的运算性质
第一组
式 log28 log232 log2(8×32)
值
猜想性质
3
5
8
log28+log232 =log2(8×32)
logaM+logaN=loga(M·N)
第二组
式 lg1000 lg100 000
值
猜想性质
3
5
-2
lg1000-lg100 000=
lg
3
10
5
10
logaM-logaN=loga
第三组
式 log335 5·log33
值
猜想性质
5
5
log335=5log33
logaMn = nlogaM
设logaM=m,logaN=n,则am=M,an=N,
(1). loga(M·N)= logaM+logaN
∴MN=am·an=am+n,
∴loga(MN)=m+n=logaM+logaN.
(2). loga =logaM-logaN
积对数等于对数之和.
商对数等于对数之差.
设logaM=p,logaN=q, M= , N=
a
p
a
q
a
p-q
M
N
=
loga =logaM-logaN
(3). logaMn = nlogaM
n次幂的对数等于n倍的对数.
设logaM=p,则 M= , Mn=
a
p
a
np
logaMn =np
logaMn = nlogaM
※ 对数运算公式几个注意点:
1) 简易语言表达:“积的对数=对数的和”,………;
2) 真数的取值必须是(0,+∞);
3) 有时公式可以可逆;
4)loga(M·N)≠ logaM·logaN
loga(M±N)≠ logaM±logaN
5)logaMn ≠( logaM )n
解:原式=log247 +log225
=7log24 +5log22
=7log222+5
=19
解:原式= lg100
= lg102
= lg10
=
1
5
1
5
2
5
2
5
解:原式=lg2+lg7-2lg7+2lg3+lg7-lg2-2lg3
=0
解:原式=2lg5+2lg2+lg5(2lg2+lg5)+(lg2)2
=2(lg5+lg2)+2lg5·lg2+(lg5)2+(lg2)2
=2+(lg2+lg5)2
=3.
知识点2
换底公式
想一想
log25
log23
=x
设 ,则log25=xlog23=log23x ,3x=5 ,x=log35
log25
log23
=
log35
1
例2.已知log189=a,18b=5,求log3645.
解 方法一 ∵log189=a,18b=5,∴log185=b,
( )
( )
解 方法二 ∵log189=a,18b=5,∴log185=b,
( )
( )
方法三 ∵log189=a,18b=5,∴lg 9=alg 18,lg 5=blg 18,
在利用换底公式进行化简求值时,一般情况是根据题中所给的对数式的具体特点选择恰当的底数进行换底,如果所给的对数式中的底数和真数互不相同,我们可以选择以10为底数进行换底.
跟踪训练 已知log23=a,log37=b,用a,b表示log4256.
又∵log37=b,
题型一
对数运算性质的应用
题型一
对数换底公式的应用
2
x
=m
x=log2m
1
x
=logm2
5
y
=m
y=log5m
1
y
=logm5
1
x
1
y
+ =2
logm2+logm5=logm10=2
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
