北师大版 数学七年级下册 第四章 三角形中的常用辅助线 讲义(pdf版、含答案)
文档属性
| 名称 | 北师大版 数学七年级下册 第四章 三角形中的常用辅助线 讲义(pdf版、含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 663.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-16 19:15:41 | ||
图片预览



文档简介
F002-三角形中的常用辅助线
三角形中常见辅助线的作法:
①延长中线构造全等三角形;
②利用翻折,构造全等三角形;
③引平行线(或平移)构造全等三角形;
④作连线构造等腰三角形。
若遇到三角形的中线,可倍长中线,使延长线
段与原中线长相等,构造全等三角形,利用的思维
模式是全等变换中的“旋转”(中心对称)。
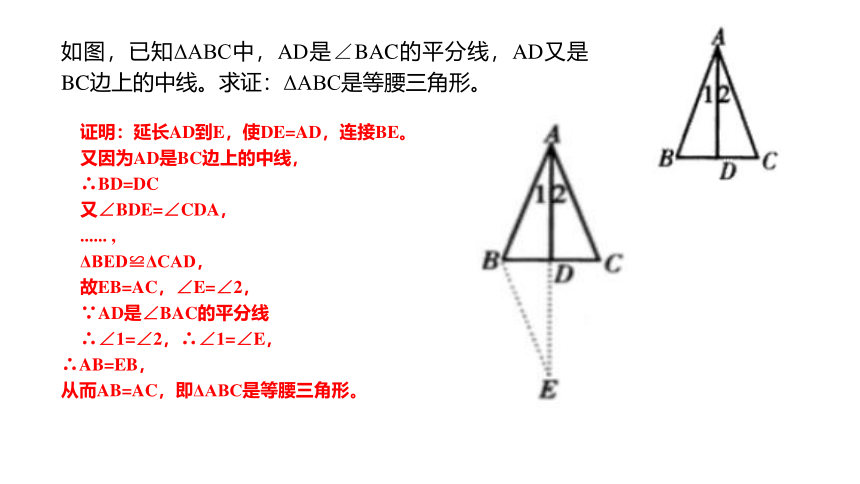
如图,已知ΔABC中,AD是∠BAC的平分线,AD又是
BC边上的中线。求证:ΔABC是等腰三角形。
证明:延长AD到E,使DE=AD,连接BE。
又因为AD是BC边上的中线,
∴BD=DC
又∠BDE=∠CDA,
...... ,
ΔBED≌ΔCAD,
故EB=AC,∠E=∠2,
∵AD是∠BAC的平分线
∴∠1=∠2,∴∠1=∠E,
∴AB=EB,
从而AB=AC,即ΔABC是等腰三角形。
过图形上某一点作特定的平行线,构造全
等三角形,利用的思维模式是全等变换中的
“平移”或“翻转折叠”。
全等三角形常见辅助线:作平行线
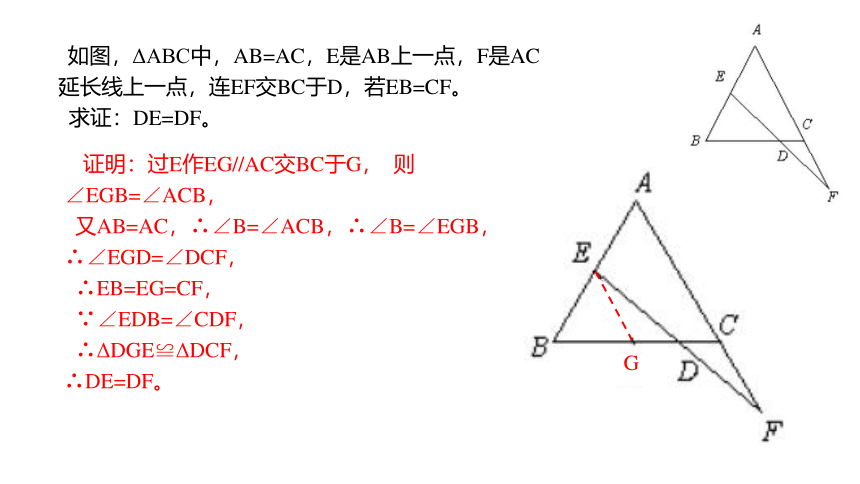
如图,ΔABC中,AB=AC,E是AB上一点,F是AC
延长线上一点,连EF交BC于D,若EB=CF。
求证:DE=DF。
证明:过E作EG//AC交BC于G, 则
∠EGB=∠ACB,
又AB=AC,∴∠B=∠ACB,∴∠B=∠EGB,
∴∠EGD=∠DCF,
∴EB=EG=CF,
∵∠EDB=∠CDF,
∴ΔDGE≌ΔDCF,
G
∴DE=DF。
如图,ΔABC中,AB=AC,E是AB上一点,F是AC延长线上一
点,连EF交BC于D,若EB=CF。 求证:DE=DF。
此题的辅助线还可以有以下几种作法:
截长法与补短法,具体作法是在某条线段上截取一条
线段与特定线段相等,或是将某条线段延长,使之与特定
线段相等,再利用三角形全等的有关性质加以说明。这种
作法,适合于证明线段的和、差、倍、分等类的题目。
遇到求证一条线段等于另两条线段之和时,一
般方法是截长法或补短法:
截长:在长线段中截取一段等于另两条中的一条,
然后证明剩下部分等于另一条;
补短:将一条短线段延长,延长部分等于另一条短
线段,然后证明新线段等于长线段。
如图,D为等腰 ABC底边BC上任意一点,DE⊥AB于E,DF ⊥ AC于
F,BH为腰AC上的高,求证:DE+DF=BH.
截长 A
H
E
F
B
D C
如图,D为等腰 ABC底边BC上任意一点,DE⊥AB于E,DF ⊥ AC于
F,BH为腰AC上的高,求证:DE+DF=BH.
补短 A
H
E
F
B
D C
如图,D为正 ABC内部任意一点,DE⊥AB于E,DF⊥BC于F, DG⊥AC
于G, BH为边AC上的高,求证:DE+DF+DG=BH.
A
H
E
G
D
B C
F
#面积桥
如图,D为正 ABC内部任意一点,DE⊥AB于E,DF⊥BC于F, DG⊥AC
于G, BH为边AC上的高,求证:DE+DF+DG=BH.
A
H
E
G
D
B C
F
#面积桥
如图,D为等腰 ABC底边BC上任意一点,DE⊥AB于E,DF ⊥ AC于
F,BH为腰AC上的高,求证:DE+DF=BH.
A
H
E
F
B
D C
ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交BC于P,
BQ平分∠ABC交AC于Q,求证:AB+BP=BQ+AQ。
证明:如图(1),过O作OD∥BC交AB于D,
∴∠ADO=∠ABC=180°-60°-40°=80°, D
又∵∠AQO=∠C+∠QBC=80°,
∴∠ADO=∠AQO,
又∵∠DAO=∠QAO,OA=AO,.....
∴ ADO≌ AQO,
∴OD=OQ,AD=AQ,
又∵OD∥BP, ∴∠PBO=∠DOB,
又∵∠PBO=∠DBO, ∴∠DBO=∠DOB,
∴BD=OD,
又∵∠BPA=∠C+∠PAC=70°,
∠BOP=∠OBA+∠BAO=70°,
∴∠BOP=∠BPO,∴BP=OB,
∴AB+BP=AD+DB+BP=AQ+OQ+BO=AQ+BQ。
ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交BC于
P,BQ平分∠ABC交AC于Q,求证:AB+BP=BQ+AQ。 D
本题也可以在AB上截取AD=AQ,连OD,
构造全等三角形,即“截长法”。
ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交BC
于P,BQ平分∠ABC交AC于Q,求证:AB+BP=BQ+AQ。
本题利用“平行法”的解法也较多,举例如下:
① 如 图 ( 2 ) , 过 O 作 OD∥BC 交 AC 于 D , 则
ADO≌ ABO从而得以解决。
ABC中,∠BAC=60°,∠C=40°,AP平分
∠BAC交BC于P,BQ平分∠ABC交AC于Q,
E
求证: DAB+BP=BQ+AQ。
ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交
BC于P,BQ平分∠ABC交AC于Q,求证:
AB+BP=BQ+AQ。
ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交BC
于P,BQ平分∠ABC交AC于Q,求证:AB+BP=BQ+AQ。
④如图(5),过P作PD∥BQ交AC于D,则
ABP≌ ADP从而得以解决。
小 结
通过一题的多种辅助线添加方法,体会添加辅助线的目的在于构造全等三
角形。而不同的添加方法实际是从不同途径来实现线段的转移的,体会构造
的全等三角形在转移线段中的作用。从变换的观点可以看到,不论是作平行
线还是倍长中线,实质都是对三角形作了一个以中点为旋转中心的旋转变
换或是以某一直线为轴对三角形进行翻折构造了全等三角形。
已知:如图,AD ∕ ∕ BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的延长线交
AP于D, 求证:AD+BC=AB.
辅助线作法之“截长补短”
“截长”:
在AB上取点F,使AF=AD,连EF,……
F
已知:如图,AD ∕ ∕ BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的延长线交
AP于D, 求证:AD+BC=AB.
辅助线作法之“截长补短”
F “补短”: 延长BE交AP于F,……
已知:如图,AD ∕ ∕ BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的延长线交
AP于D, 求证:AD+BC=AB.
辅助线作法之“截长补短”
“补短”: 延长AE交BC延长线于F,……
F
如图, 在三角形ABC中,BC上的高为AD,且∠B=2∠C, “截长补短”
求证:CD=AB+BD.
A
“截长”:
B D E C
“截长补短”
如图, 在三角形ABC中,BC上的高为AD,且∠B=2∠C,
求证:CD=AB+BD.
“补短”:
延长DB至F,使BF=BA,连接AF……
A
F B D C
如图:在四边形ABCD中,点E在边CD上,连接AE、BE并延长AE交BC的
延长线于点F,给出下列5个关系式::①AD∥BC,②DE=EC,③
∠1=∠2,④∠3=∠4,⑤AD+BC=AB。将其中三个关系式作为已知,另外
两个作为结论,构成正确的命题。请用序号写出两个正确的命题:(书写
形式:如果……那么……)(1) ;(2) .
如果①②③, 那么④⑤. A D
1
如果①③④, 那么②⑤. 2
E
3
B 4 F
(第18题) C
已知,ΔABC和ΔECD都是等边三角形,且点B,C,D在一条直线上,
AC与BE相交于M,CE与AD相交于N,试判定ΔCMN的形状.
E
A
解:ΔCMN是等边三角形.
M N
证明:
B D
(1)先证∠ACE=60°; C
(2)证明ΔBCE≌ΔACD→∠BEC=∠ADC;
(3)在证ΔMCE≌ΔNCD→CM=CN.
已知:如图,∠1=∠2 ,CD=DE,EF ∕ ∕ AB,求证:EF=AC。
证明:延长FD至G,使 DG=DF, 连接 CG,
……
G
在ΔABC中,∠ACB=90°,AC=BC,
直线MN经过点C,AD⊥MN于D,
BE⊥ MN于E ,
(1)当MN绕点C旋转到图1位置时,
求证:
①ΔADC≌ΔCEB;
②DE=AD+BE;
(2)当MN绕点C旋转到图2位置时,
(1)中的结论还成立呢?若成立,请
给出证明,若不成立,说明理由。
在ΔABC中,∠ACB=90°,AC=BC,直线
MN经过点C,AD⊥MN于D,BE⊥ MN于E ,
(1)当MN绕点C旋转到图1位置时,求证:
①ΔADC≌ΔCEB;
②DE=AD+BE;
(2)当MN绕点C旋转到图2位置时,(1)中的 B
结论还成立呢?若成立,请给出证明,若不
成立,说明理由。
DE=AD-BE
已知点A,E,F,C在同一条直线上,且AE=CF,过E F两点分别作DE⊥AC,
BF⊥AC,且AB=CD,(1)求证:BD平分 EF;(2)若将ΔDEC的边EC沿AC
方向移动,变化为2时,其余条件不变,上述结论是否成立,说明理由.
B
B
F E C
E F C
A G
A G
图2
D
图1
D
知识小结
1、全等三角形的概念—— 能够重合的三角形
2、全等三角形的性质—— 对应边相等、对应角相等
3、全等三角形的判定方法
(SSS) (SAS)(ASA)(AAS)(HL)
有何共性?
要判定两个三角形全等,至少要有一组对应边相等。
判定思路小结
三角形全等判定方法的思路:
已知条件 可选择的判定方法
两组边对应相等 SSS SAS HL
两组角对应相等 ASA AAS
一边一角对应相等 SAS ASA AAS
三角形全等的证题思路:
找夹角→ SAS
①已知两边 找另一边→ SSS
找直角→HL
边为角的对边→找任一角→ AAS
②已知一边一角 找夹角的另一边→ SAS
边为角的邻边 找边的对角→ AAS
找夹角的另一角→ ASA
找夹边→ ASA
③已知两角
找任一边→ AAS
1.证明两个三角形全等,要结合题目的条件和结论,选择恰当的判
定方法
2.全等三角形,是证明两条线段或两个角相等的重要方法之一,证
明时
①要观察待证的线段或角,在哪两个可能全等的三角形中。
②分析要证两个三角形全等,已有什么条件,还缺什么条件。
③有公共边的,公共边一定是对应边,有公共角的,公共角一
定是对应角,有对顶角,对顶角也是对应角
总之,证明过程中能用简单方法的就不要绕弯路。
三角形中常见辅助线的作法:
①延长中线构造全等三角形;
②利用翻折,构造全等三角形;
③引平行线(或平移)构造全等三角形;
④作连线构造等腰三角形。
若遇到三角形的中线,可倍长中线,使延长线
段与原中线长相等,构造全等三角形,利用的思维
模式是全等变换中的“旋转”(中心对称)。
如图,已知ΔABC中,AD是∠BAC的平分线,AD又是
BC边上的中线。求证:ΔABC是等腰三角形。
证明:延长AD到E,使DE=AD,连接BE。
又因为AD是BC边上的中线,
∴BD=DC
又∠BDE=∠CDA,
...... ,
ΔBED≌ΔCAD,
故EB=AC,∠E=∠2,
∵AD是∠BAC的平分线
∴∠1=∠2,∴∠1=∠E,
∴AB=EB,
从而AB=AC,即ΔABC是等腰三角形。
过图形上某一点作特定的平行线,构造全
等三角形,利用的思维模式是全等变换中的
“平移”或“翻转折叠”。
全等三角形常见辅助线:作平行线
如图,ΔABC中,AB=AC,E是AB上一点,F是AC
延长线上一点,连EF交BC于D,若EB=CF。
求证:DE=DF。
证明:过E作EG//AC交BC于G, 则
∠EGB=∠ACB,
又AB=AC,∴∠B=∠ACB,∴∠B=∠EGB,
∴∠EGD=∠DCF,
∴EB=EG=CF,
∵∠EDB=∠CDF,
∴ΔDGE≌ΔDCF,
G
∴DE=DF。
如图,ΔABC中,AB=AC,E是AB上一点,F是AC延长线上一
点,连EF交BC于D,若EB=CF。 求证:DE=DF。
此题的辅助线还可以有以下几种作法:
截长法与补短法,具体作法是在某条线段上截取一条
线段与特定线段相等,或是将某条线段延长,使之与特定
线段相等,再利用三角形全等的有关性质加以说明。这种
作法,适合于证明线段的和、差、倍、分等类的题目。
遇到求证一条线段等于另两条线段之和时,一
般方法是截长法或补短法:
截长:在长线段中截取一段等于另两条中的一条,
然后证明剩下部分等于另一条;
补短:将一条短线段延长,延长部分等于另一条短
线段,然后证明新线段等于长线段。
如图,D为等腰 ABC底边BC上任意一点,DE⊥AB于E,DF ⊥ AC于
F,BH为腰AC上的高,求证:DE+DF=BH.
截长 A
H
E
F
B
D C
如图,D为等腰 ABC底边BC上任意一点,DE⊥AB于E,DF ⊥ AC于
F,BH为腰AC上的高,求证:DE+DF=BH.
补短 A
H
E
F
B
D C
如图,D为正 ABC内部任意一点,DE⊥AB于E,DF⊥BC于F, DG⊥AC
于G, BH为边AC上的高,求证:DE+DF+DG=BH.
A
H
E
G
D
B C
F
#面积桥
如图,D为正 ABC内部任意一点,DE⊥AB于E,DF⊥BC于F, DG⊥AC
于G, BH为边AC上的高,求证:DE+DF+DG=BH.
A
H
E
G
D
B C
F
#面积桥
如图,D为等腰 ABC底边BC上任意一点,DE⊥AB于E,DF ⊥ AC于
F,BH为腰AC上的高,求证:DE+DF=BH.
A
H
E
F
B
D C
ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交BC于P,
BQ平分∠ABC交AC于Q,求证:AB+BP=BQ+AQ。
证明:如图(1),过O作OD∥BC交AB于D,
∴∠ADO=∠ABC=180°-60°-40°=80°, D
又∵∠AQO=∠C+∠QBC=80°,
∴∠ADO=∠AQO,
又∵∠DAO=∠QAO,OA=AO,.....
∴ ADO≌ AQO,
∴OD=OQ,AD=AQ,
又∵OD∥BP, ∴∠PBO=∠DOB,
又∵∠PBO=∠DBO, ∴∠DBO=∠DOB,
∴BD=OD,
又∵∠BPA=∠C+∠PAC=70°,
∠BOP=∠OBA+∠BAO=70°,
∴∠BOP=∠BPO,∴BP=OB,
∴AB+BP=AD+DB+BP=AQ+OQ+BO=AQ+BQ。
ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交BC于
P,BQ平分∠ABC交AC于Q,求证:AB+BP=BQ+AQ。 D
本题也可以在AB上截取AD=AQ,连OD,
构造全等三角形,即“截长法”。
ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交BC
于P,BQ平分∠ABC交AC于Q,求证:AB+BP=BQ+AQ。
本题利用“平行法”的解法也较多,举例如下:
① 如 图 ( 2 ) , 过 O 作 OD∥BC 交 AC 于 D , 则
ADO≌ ABO从而得以解决。
ABC中,∠BAC=60°,∠C=40°,AP平分
∠BAC交BC于P,BQ平分∠ABC交AC于Q,
E
求证: DAB+BP=BQ+AQ。
ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交
BC于P,BQ平分∠ABC交AC于Q,求证:
AB+BP=BQ+AQ。
ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交BC
于P,BQ平分∠ABC交AC于Q,求证:AB+BP=BQ+AQ。
④如图(5),过P作PD∥BQ交AC于D,则
ABP≌ ADP从而得以解决。
小 结
通过一题的多种辅助线添加方法,体会添加辅助线的目的在于构造全等三
角形。而不同的添加方法实际是从不同途径来实现线段的转移的,体会构造
的全等三角形在转移线段中的作用。从变换的观点可以看到,不论是作平行
线还是倍长中线,实质都是对三角形作了一个以中点为旋转中心的旋转变
换或是以某一直线为轴对三角形进行翻折构造了全等三角形。
已知:如图,AD ∕ ∕ BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的延长线交
AP于D, 求证:AD+BC=AB.
辅助线作法之“截长补短”
“截长”:
在AB上取点F,使AF=AD,连EF,……
F
已知:如图,AD ∕ ∕ BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的延长线交
AP于D, 求证:AD+BC=AB.
辅助线作法之“截长补短”
F “补短”: 延长BE交AP于F,……
已知:如图,AD ∕ ∕ BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的延长线交
AP于D, 求证:AD+BC=AB.
辅助线作法之“截长补短”
“补短”: 延长AE交BC延长线于F,……
F
如图, 在三角形ABC中,BC上的高为AD,且∠B=2∠C, “截长补短”
求证:CD=AB+BD.
A
“截长”:
B D E C
“截长补短”
如图, 在三角形ABC中,BC上的高为AD,且∠B=2∠C,
求证:CD=AB+BD.
“补短”:
延长DB至F,使BF=BA,连接AF……
A
F B D C
如图:在四边形ABCD中,点E在边CD上,连接AE、BE并延长AE交BC的
延长线于点F,给出下列5个关系式::①AD∥BC,②DE=EC,③
∠1=∠2,④∠3=∠4,⑤AD+BC=AB。将其中三个关系式作为已知,另外
两个作为结论,构成正确的命题。请用序号写出两个正确的命题:(书写
形式:如果……那么……)(1) ;(2) .
如果①②③, 那么④⑤. A D
1
如果①③④, 那么②⑤. 2
E
3
B 4 F
(第18题) C
已知,ΔABC和ΔECD都是等边三角形,且点B,C,D在一条直线上,
AC与BE相交于M,CE与AD相交于N,试判定ΔCMN的形状.
E
A
解:ΔCMN是等边三角形.
M N
证明:
B D
(1)先证∠ACE=60°; C
(2)证明ΔBCE≌ΔACD→∠BEC=∠ADC;
(3)在证ΔMCE≌ΔNCD→CM=CN.
已知:如图,∠1=∠2 ,CD=DE,EF ∕ ∕ AB,求证:EF=AC。
证明:延长FD至G,使 DG=DF, 连接 CG,
……
G
在ΔABC中,∠ACB=90°,AC=BC,
直线MN经过点C,AD⊥MN于D,
BE⊥ MN于E ,
(1)当MN绕点C旋转到图1位置时,
求证:
①ΔADC≌ΔCEB;
②DE=AD+BE;
(2)当MN绕点C旋转到图2位置时,
(1)中的结论还成立呢?若成立,请
给出证明,若不成立,说明理由。
在ΔABC中,∠ACB=90°,AC=BC,直线
MN经过点C,AD⊥MN于D,BE⊥ MN于E ,
(1)当MN绕点C旋转到图1位置时,求证:
①ΔADC≌ΔCEB;
②DE=AD+BE;
(2)当MN绕点C旋转到图2位置时,(1)中的 B
结论还成立呢?若成立,请给出证明,若不
成立,说明理由。
DE=AD-BE
已知点A,E,F,C在同一条直线上,且AE=CF,过E F两点分别作DE⊥AC,
BF⊥AC,且AB=CD,(1)求证:BD平分 EF;(2)若将ΔDEC的边EC沿AC
方向移动,变化为2时,其余条件不变,上述结论是否成立,说明理由.
B
B
F E C
E F C
A G
A G
图2
D
图1
D
知识小结
1、全等三角形的概念—— 能够重合的三角形
2、全等三角形的性质—— 对应边相等、对应角相等
3、全等三角形的判定方法
(SSS) (SAS)(ASA)(AAS)(HL)
有何共性?
要判定两个三角形全等,至少要有一组对应边相等。
判定思路小结
三角形全等判定方法的思路:
已知条件 可选择的判定方法
两组边对应相等 SSS SAS HL
两组角对应相等 ASA AAS
一边一角对应相等 SAS ASA AAS
三角形全等的证题思路:
找夹角→ SAS
①已知两边 找另一边→ SSS
找直角→HL
边为角的对边→找任一角→ AAS
②已知一边一角 找夹角的另一边→ SAS
边为角的邻边 找边的对角→ AAS
找夹角的另一角→ ASA
找夹边→ ASA
③已知两角
找任一边→ AAS
1.证明两个三角形全等,要结合题目的条件和结论,选择恰当的判
定方法
2.全等三角形,是证明两条线段或两个角相等的重要方法之一,证
明时
①要观察待证的线段或角,在哪两个可能全等的三角形中。
②分析要证两个三角形全等,已有什么条件,还缺什么条件。
③有公共边的,公共边一定是对应边,有公共角的,公共角一
定是对应角,有对顶角,对顶角也是对应角
总之,证明过程中能用简单方法的就不要绕弯路。
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
