九年级数学上册第24章《圆》综合测试题(Word版含答案)
文档属性
| 名称 | 九年级数学上册第24章《圆》综合测试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 569.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-16 21:51:51 | ||
图片预览


文档简介
第24章《圆》综合测试题
一、单选题
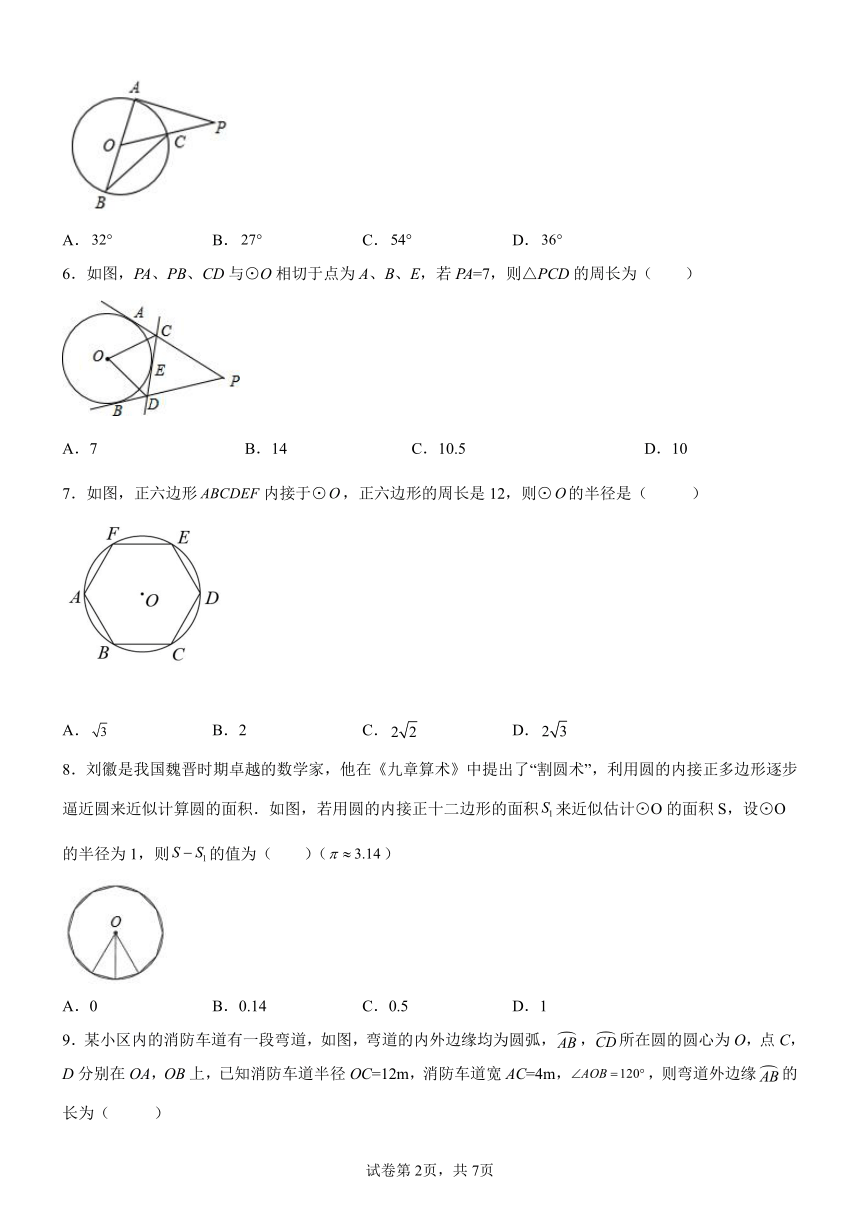
1.过圆上一点可以作出圆的最长的弦有( )条.
A.1 B.2 C.3 D.4
2.AB为⊙O的直径,弦CD⊥AB于点E,已知CD=16,OE=6,则⊙O的直径为( )
A.8 B.10 C.16 D.20
3.如图,已知AB是半圆O的直径,∠BAC=32 ,D是弧AC的中点,那么∠DAC的度数是( )
A.25 B.29 C.30 D.32°
4.如图,以点为圆心作圆恰好与直线相切,则与半径相等的线段是( )
A. B. C. D.
5.如图所示,AB是⊙O的直径,PA切⊙O于点A,线段PO交⊙O于点C,连接BC,若,则等于( )
A. B. C. D.
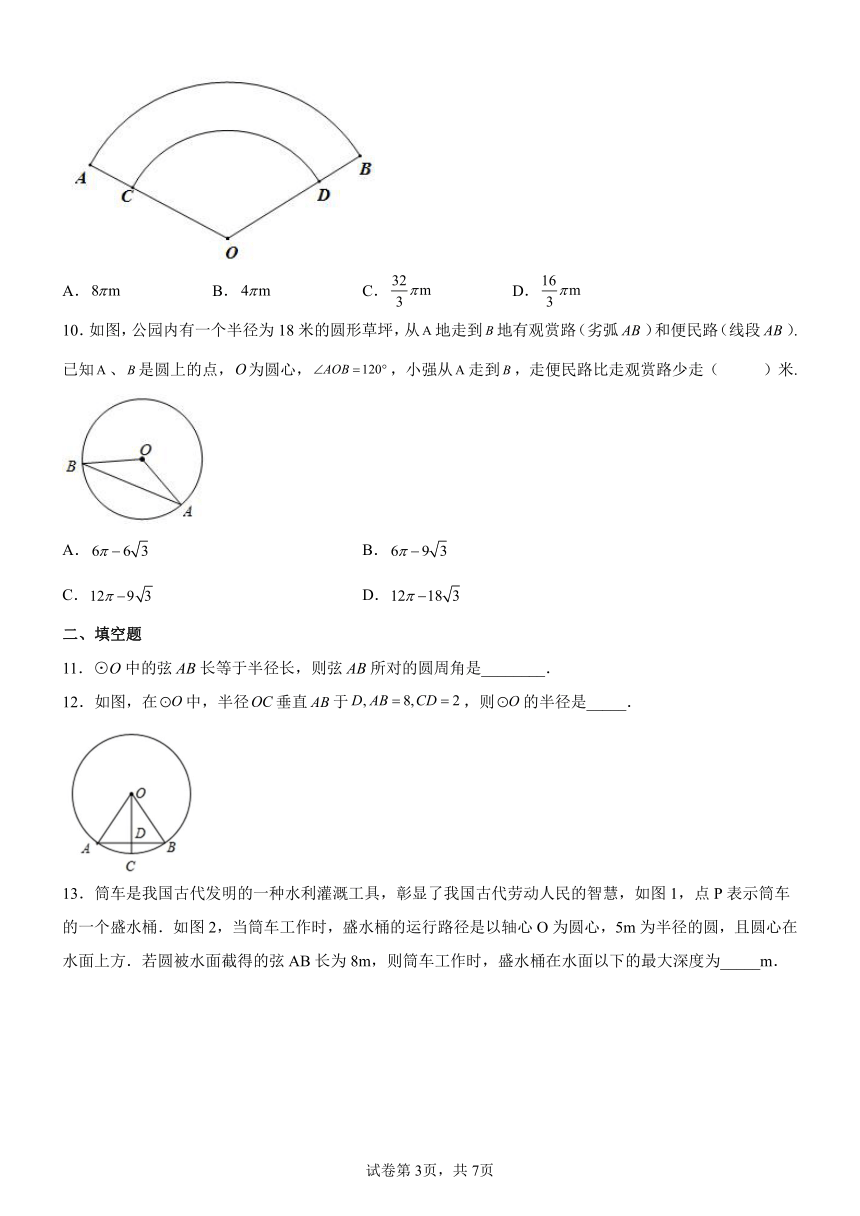
6.如图,PA、PB、CD与⊙O相切于点为A、B、E,若PA=7,则△PCD的周长为( )
A.7 B.14 C.10.5 D.10
7.如图,正六边形内接于⊙,正六边形的周长是12,则⊙的半径是( )
A. B.2 C. D.
8.刘徽是我国魏晋时期卓越的数学家,他在《九章算术》中提出了“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积.如图,若用圆的内接正十二边形的面积来近似估计⊙O的面积S,设⊙O的半径为1,则的值为( )()
A.0 B.0.14 C.0.5 D.1
9.某小区内的消防车道有一段弯道,如图,弯道的内外边缘均为圆弧,,所在圆的圆心为O,点C,D分别在OA,OB上,已知消防车道半径OC=12m,消防车道宽AC=4m,,则弯道外边缘的长为( )
A. B. C. D.
10.如图,公园内有一个半径为18米的圆形草坪,从地走到地有观赏路(劣弧)和便民路(线段).已知、是圆上的点,为圆心,,小强从走到,走便民路比走观赏路少走( )米.
A. B.
C. D.
二、填空题
11.⊙O中的弦AB长等于半径长,则弦AB所对的圆周角是________.
12.如图,在中,半径垂直于,则的半径是_____.
13.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,则筒车工作时,盛水桶在水面以下的最大深度为_____m.
14.如图,,是的切线,切点分别是点和,是的直径.若°,,则的长为________.
15.刘徽是我国魏晋时期卓越的数学家,他在《九章算术》中提出了“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积,如图,若用圆的内接正十二边形的面积来近似估计的面积,设的半径为1,则__________.
16.如图,在中,,以点A为圆心,2为半径的与BC相切于点D,交AB于E,交AC于F,点P是上的一点,且,则图中阴影部分的面积是_______(结果保留).
三、解答题
17.如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP∶AP=1∶5.求CD的长.
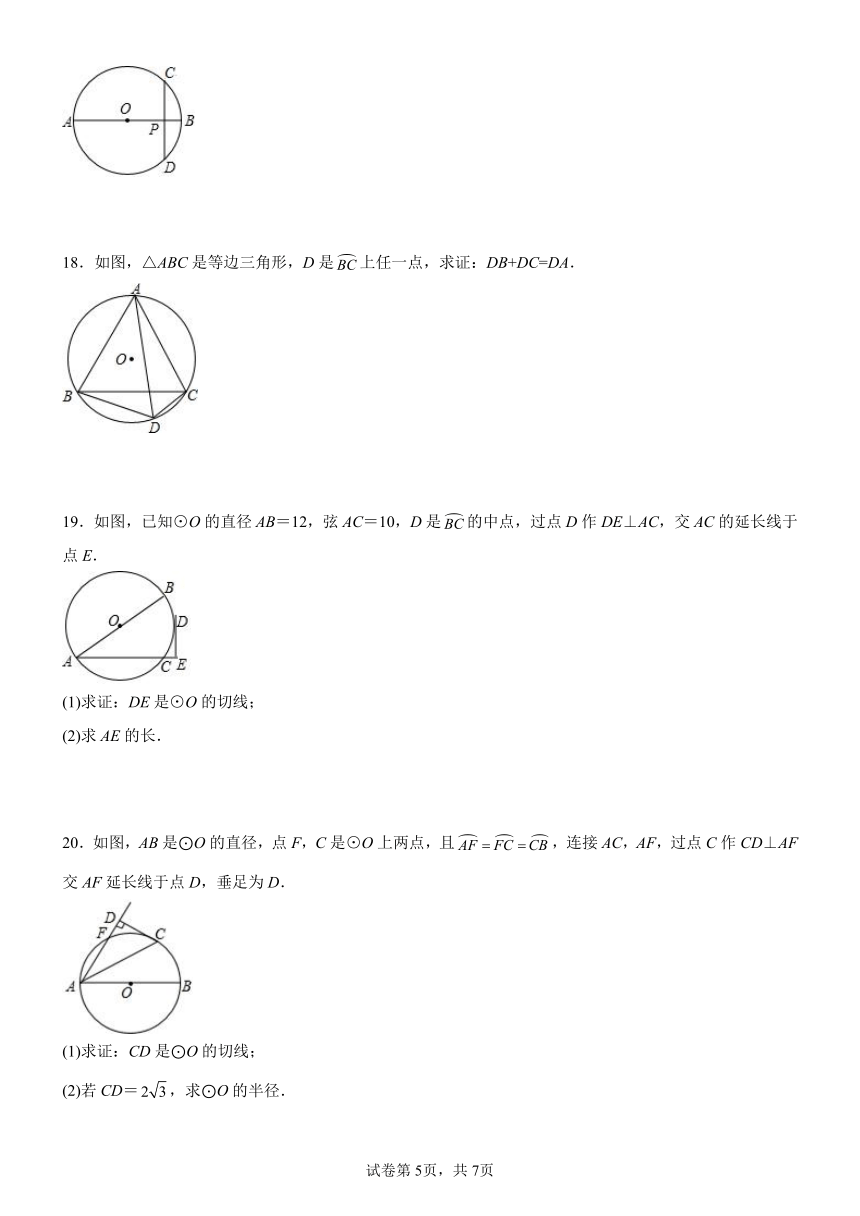
18.如图,△ABC是等边三角形,D是上任一点,求证:DB+DC=DA.
19.如图,已知⊙O的直径AB=12,弦AC=10,D是的中点,过点D作DE⊥AC,交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)求AE的长.
20.如图,AB是⊙O的直径,点F,C是⊙O上两点,且,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD=,求⊙O的半径.
21.某校编排的一个舞蹈需要五把和图1形状、大小完全相同的绸扇.学校现有三把符合要求的绸扇,将这三把绸扇完全展开刚好组成图2所示的一朵圆形的花.请你算一算:再做两把这样的绸扇至少需要多少绸布?(单面制作,不考虑绸扇的折皱,结果用含π的式子表示)
22.如图,为的直径,C为上一点,弦的延长线与过点C的切线互相垂直,垂足为D,,连接.
(1)求的度数;
(2)若,求的长.
23.等边三角形的边长为1厘米,面积为0.43平方厘米.以点为圆心,长为半径在三角形外画弧,交的延长线于点,形成扇形;以点为圆心,长为半径画弧,交的延长线于点,形成扇形;以点为圆心,长为半径画弧,交的延长线于点,形成扇形.
(1)求所得的图形的周长;(结果保留)
(2)照此规律画至第十个扇形,求所围成的图形的面积以及所画出的所有弧长的和.(结果保留)
24.如图,在等腰中,,AD是的角平分线,且,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F,
(1)求由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积;
(2)将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
2.D
3.B
4.B
5.B
6.B
7.B
8.B
9.C
10.D
11.30°或150°
12.5
13.2
14.
15.
16.
17.解:连接OC,
∵⊙O的直径AB=12,
∴OB=AB=6,
∴OC=6,
∵BP∶AP=1∶5,
∴BP=AB=×12=2,
∴OP=OB﹣BP=6﹣2=4,
∵CD⊥AB,
∴CD=2PC,
在Rt△OPC中,
∵OC=6,OP=4,
∴PC===2,
∴CD=2PC=4.
18.解:延长DB至点E,使BE=DC,连结AE
∵△ABC是等边三角形
∴∠ACB=∠ABC=60°,AB=AC
∴∠ADB=∠ACB=60°
∵四边形ABDC是圆内接四边形
∴∠ABE=∠ACD
在△AEB和△ADC中,
∴△AEB≌△ADC
∴AE=AD
∵∠ADB=60°
∴△AED是等边三角形
∴AD=DE=DB+BE
∵BE=DC
∴DB+DC=DA.
19.
(1)
证明:如图:连接OD,
是的中点,
,
,
,
,
,
,
,
又是⊙O的半径
DE是⊙O的切线;
(2)
解:如图:过点O作于点F,
,
,
,
四边形OFED是矩形,
,
.
20.
(1)
连接OC,如图,
∵,
∴∠FAC=∠BAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠FAC=∠OCA,
∴OC//AF,
∵CD⊥AF,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)
连接BC,如图,
∵AB为直径,
∴∠ACB=90°,
∵,
∴∠BOC=×180°=60°,
∴∠BAC=30°,
∴∠DAC=30°,
在Rt△ADC中,CD=,
∴AC=2CD=,
在Rt△ACB中,BC2+AC2=AB2,
即()2+(AB)2=AB2,
∴AB=8,
∴⊙O的半径为4.
21.三把绸扇完全展开刚好组成了一个圆,
∴可得大圆的半径为30cm;
可知小圆的半径为12cm.
∴S大圆=πr =30π=900π;S小圆=πr=12π=144π.
∴S绸面=S大圆-S小圆=900π-144π=756π.
∴二把绸扇所需的绸布面积是: ×S绸面=×756π=504π(cm).
答:再做两把这样的绸扇至少需要的绸布.
22.解:(1)连接OC,如图,
∵CD是⊙O的切线,
∴OC⊥CD,
∵AE⊥CD,
∴OC∥AE,
∴∠DAC=∠OCA,
∵OA=OC,∠CAD=35°,
∴∠OAC=∠OCA=∠CAD=35°,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠B=90°-∠OAC=55°;
(2)连接OE,OC,如图,
由(1)得∠EAO=∠OAC+∠CAD=70°,
∵OA=OE,
∴∠AEO∠EAO70°,
∵OC∥AE,
∴∠COE=∠AEO=70°,
∴AB=2,则OC=OE=1,
∴的长为.
23.(1)由已知得:扇形ADC的半径长为1,圆心角为120°;扇形DBE半径长为2,圆心角为120°;扇形ECF半径长为3,圆心角为120°.
故据弧长公式可得:扇形ADC弧长;扇形DBE弧长;扇形ECF弧长;
故图形CDEFC的周长为:.
(2)根据扇形面积公式可得:
第一个扇形的面积为,由上一问可知其弧长为;
第二个扇形的面积为,弧长为;
第三个扇形的面积为,弧长为;
总结规律可得第个扇形面积为,第个扇形弧长为.
故画至第十个图形所围成的图形面积和为:;
所有的弧长和为:.
24.∵在等腰中,,
∴,
∵AD是的角平分线,
∴,,
∴,
∴,
∴由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积.
(2)设圆锥的底面圆的半径为r,
根据题意得,解得,
这个圆锥的高.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.过圆上一点可以作出圆的最长的弦有( )条.
A.1 B.2 C.3 D.4
2.AB为⊙O的直径,弦CD⊥AB于点E,已知CD=16,OE=6,则⊙O的直径为( )
A.8 B.10 C.16 D.20
3.如图,已知AB是半圆O的直径,∠BAC=32 ,D是弧AC的中点,那么∠DAC的度数是( )
A.25 B.29 C.30 D.32°
4.如图,以点为圆心作圆恰好与直线相切,则与半径相等的线段是( )
A. B. C. D.
5.如图所示,AB是⊙O的直径,PA切⊙O于点A,线段PO交⊙O于点C,连接BC,若,则等于( )
A. B. C. D.
6.如图,PA、PB、CD与⊙O相切于点为A、B、E,若PA=7,则△PCD的周长为( )
A.7 B.14 C.10.5 D.10
7.如图,正六边形内接于⊙,正六边形的周长是12,则⊙的半径是( )
A. B.2 C. D.
8.刘徽是我国魏晋时期卓越的数学家,他在《九章算术》中提出了“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积.如图,若用圆的内接正十二边形的面积来近似估计⊙O的面积S,设⊙O的半径为1,则的值为( )()
A.0 B.0.14 C.0.5 D.1
9.某小区内的消防车道有一段弯道,如图,弯道的内外边缘均为圆弧,,所在圆的圆心为O,点C,D分别在OA,OB上,已知消防车道半径OC=12m,消防车道宽AC=4m,,则弯道外边缘的长为( )
A. B. C. D.
10.如图,公园内有一个半径为18米的圆形草坪,从地走到地有观赏路(劣弧)和便民路(线段).已知、是圆上的点,为圆心,,小强从走到,走便民路比走观赏路少走( )米.
A. B.
C. D.
二、填空题
11.⊙O中的弦AB长等于半径长,则弦AB所对的圆周角是________.
12.如图,在中,半径垂直于,则的半径是_____.
13.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,则筒车工作时,盛水桶在水面以下的最大深度为_____m.
14.如图,,是的切线,切点分别是点和,是的直径.若°,,则的长为________.
15.刘徽是我国魏晋时期卓越的数学家,他在《九章算术》中提出了“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积,如图,若用圆的内接正十二边形的面积来近似估计的面积,设的半径为1,则__________.
16.如图,在中,,以点A为圆心,2为半径的与BC相切于点D,交AB于E,交AC于F,点P是上的一点,且,则图中阴影部分的面积是_______(结果保留).
三、解答题
17.如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP∶AP=1∶5.求CD的长.
18.如图,△ABC是等边三角形,D是上任一点,求证:DB+DC=DA.
19.如图,已知⊙O的直径AB=12,弦AC=10,D是的中点,过点D作DE⊥AC,交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)求AE的长.
20.如图,AB是⊙O的直径,点F,C是⊙O上两点,且,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD=,求⊙O的半径.
21.某校编排的一个舞蹈需要五把和图1形状、大小完全相同的绸扇.学校现有三把符合要求的绸扇,将这三把绸扇完全展开刚好组成图2所示的一朵圆形的花.请你算一算:再做两把这样的绸扇至少需要多少绸布?(单面制作,不考虑绸扇的折皱,结果用含π的式子表示)
22.如图,为的直径,C为上一点,弦的延长线与过点C的切线互相垂直,垂足为D,,连接.
(1)求的度数;
(2)若,求的长.
23.等边三角形的边长为1厘米,面积为0.43平方厘米.以点为圆心,长为半径在三角形外画弧,交的延长线于点,形成扇形;以点为圆心,长为半径画弧,交的延长线于点,形成扇形;以点为圆心,长为半径画弧,交的延长线于点,形成扇形.
(1)求所得的图形的周长;(结果保留)
(2)照此规律画至第十个扇形,求所围成的图形的面积以及所画出的所有弧长的和.(结果保留)
24.如图,在等腰中,,AD是的角平分线,且,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F,
(1)求由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积;
(2)将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
2.D
3.B
4.B
5.B
6.B
7.B
8.B
9.C
10.D
11.30°或150°
12.5
13.2
14.
15.
16.
17.解:连接OC,
∵⊙O的直径AB=12,
∴OB=AB=6,
∴OC=6,
∵BP∶AP=1∶5,
∴BP=AB=×12=2,
∴OP=OB﹣BP=6﹣2=4,
∵CD⊥AB,
∴CD=2PC,
在Rt△OPC中,
∵OC=6,OP=4,
∴PC===2,
∴CD=2PC=4.
18.解:延长DB至点E,使BE=DC,连结AE
∵△ABC是等边三角形
∴∠ACB=∠ABC=60°,AB=AC
∴∠ADB=∠ACB=60°
∵四边形ABDC是圆内接四边形
∴∠ABE=∠ACD
在△AEB和△ADC中,
∴△AEB≌△ADC
∴AE=AD
∵∠ADB=60°
∴△AED是等边三角形
∴AD=DE=DB+BE
∵BE=DC
∴DB+DC=DA.
19.
(1)
证明:如图:连接OD,
是的中点,
,
,
,
,
,
,
,
又是⊙O的半径
DE是⊙O的切线;
(2)
解:如图:过点O作于点F,
,
,
,
四边形OFED是矩形,
,
.
20.
(1)
连接OC,如图,
∵,
∴∠FAC=∠BAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠FAC=∠OCA,
∴OC//AF,
∵CD⊥AF,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)
连接BC,如图,
∵AB为直径,
∴∠ACB=90°,
∵,
∴∠BOC=×180°=60°,
∴∠BAC=30°,
∴∠DAC=30°,
在Rt△ADC中,CD=,
∴AC=2CD=,
在Rt△ACB中,BC2+AC2=AB2,
即()2+(AB)2=AB2,
∴AB=8,
∴⊙O的半径为4.
21.三把绸扇完全展开刚好组成了一个圆,
∴可得大圆的半径为30cm;
可知小圆的半径为12cm.
∴S大圆=πr =30π=900π;S小圆=πr=12π=144π.
∴S绸面=S大圆-S小圆=900π-144π=756π.
∴二把绸扇所需的绸布面积是: ×S绸面=×756π=504π(cm).
答:再做两把这样的绸扇至少需要的绸布.
22.解:(1)连接OC,如图,
∵CD是⊙O的切线,
∴OC⊥CD,
∵AE⊥CD,
∴OC∥AE,
∴∠DAC=∠OCA,
∵OA=OC,∠CAD=35°,
∴∠OAC=∠OCA=∠CAD=35°,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠B=90°-∠OAC=55°;
(2)连接OE,OC,如图,
由(1)得∠EAO=∠OAC+∠CAD=70°,
∵OA=OE,
∴∠AEO∠EAO70°,
∵OC∥AE,
∴∠COE=∠AEO=70°,
∴AB=2,则OC=OE=1,
∴的长为.
23.(1)由已知得:扇形ADC的半径长为1,圆心角为120°;扇形DBE半径长为2,圆心角为120°;扇形ECF半径长为3,圆心角为120°.
故据弧长公式可得:扇形ADC弧长;扇形DBE弧长;扇形ECF弧长;
故图形CDEFC的周长为:.
(2)根据扇形面积公式可得:
第一个扇形的面积为,由上一问可知其弧长为;
第二个扇形的面积为,弧长为;
第三个扇形的面积为,弧长为;
总结规律可得第个扇形面积为,第个扇形弧长为.
故画至第十个图形所围成的图形面积和为:;
所有的弧长和为:.
24.∵在等腰中,,
∴,
∵AD是的角平分线,
∴,,
∴,
∴,
∴由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积.
(2)设圆锥的底面圆的半径为r,
根据题意得,解得,
这个圆锥的高.
答案第1页,共2页
答案第1页,共2页
同课章节目录
