江苏省盐城东台市唐洋镇中学九年级数学下册《7.1 正切》导学案
文档属性
| 名称 | 江苏省盐城东台市唐洋镇中学九年级数学下册《7.1 正切》导学案 | 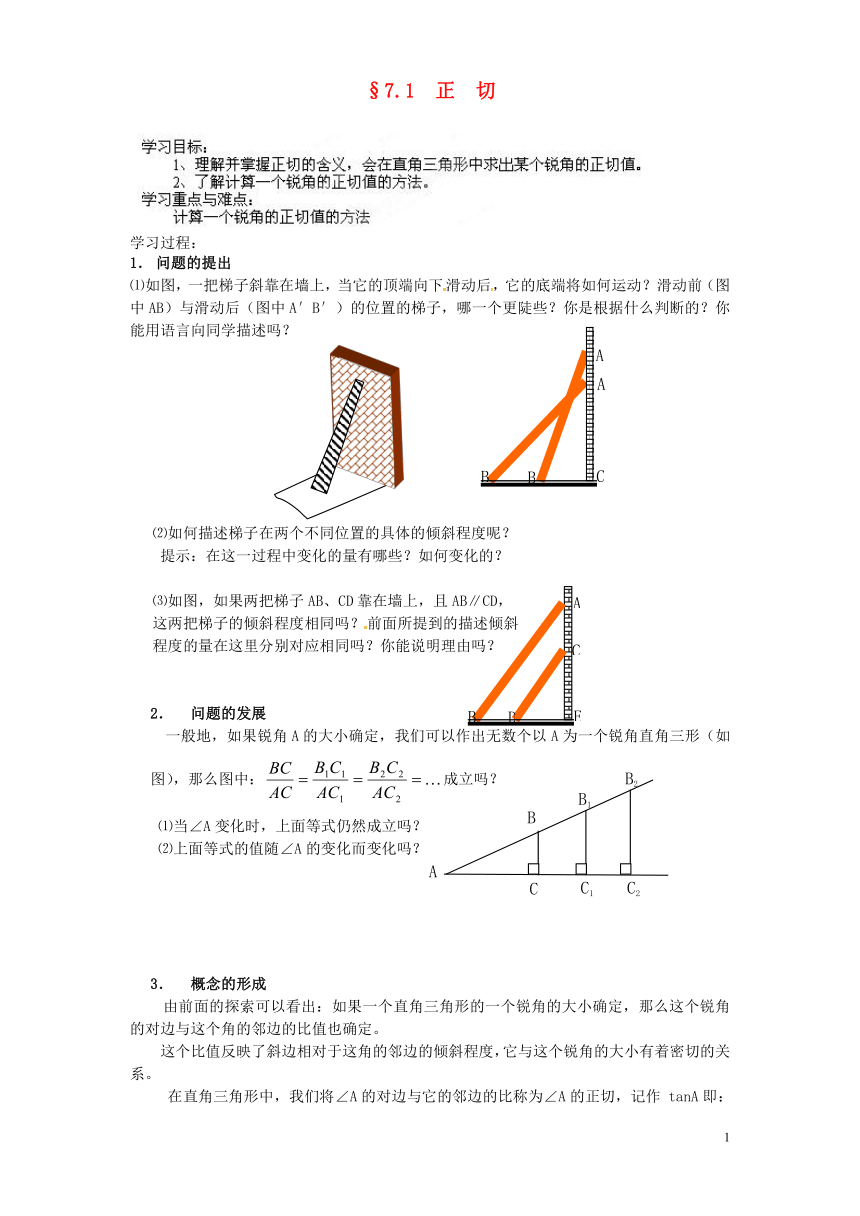 | |
| 格式 | zip | ||
| 文件大小 | 37.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-08 21:06:35 | ||
图片预览

文档简介
§7.1 正 切
学习过程:
问题的提出
⑴如图,一把梯子斜靠在墙上,当它的顶端向下滑动后,它的底端将如何运动?滑动前(图中AB)与滑动后(图中A′B′)的位置的梯子,哪一个更陡些?你是根据什么判断的?你能用语言向同学描述吗?
⑵如何描述梯子在两个不同位置的具体的倾斜程度呢?
提示:在这一过程中变化的量有哪些?如何变化的?
⑶如图,如果两把梯子AB、CD靠在墙上,且AB∥CD,
这两把梯子的倾斜程度相同吗?前面所提到的描述倾斜
程度的量在这里分别对应相同吗?你能说明理由吗?
问题的发展
一般地,如果锐角A的大小确定,我们可以作出无数个以A为一个锐角直角三形(如图),那么图中:成立吗?
⑴当∠A变化时,上面等式仍然成立吗?
⑵上面等式的值随∠A的变化而变化吗?
概念的形成
由前面的探索可以看出:如果一个直角三角形的一个锐角的大小确定,那么这个锐角的对边与这个角的邻边的比值也确定。
这个比值反映了斜边相对于这角的邻边的倾斜程度,它与这个锐角的大小有着密切的关系。
在直角三角形中,我们将∠A的对边与它的邻边的比称为∠A的正切,记作 tanA即:
4.一个锐角的正切值
⑴如图,△ABC中,AC=4,BC=3,∠C=90°,求:tanA与 tanB的值。
⑵你能用画图的方法计算一个50°角的正切的近似值吗?
据图填表:
0°
20°
30°
45°
55°
65°
75°
⑶如图,从点O出发,点P沿65°线移动,当在水平方向上向右前进了一个单位时,它在垂直方向上向上前进了 个单位。P点的坐标是 ,tan65°≈ 。
①想一想:锐角的正切值是如何随着的变化而变化的?
②关于用计算器计算正切值请课后自学。
三.巩固与拓展
A级:
⑴某楼梯的踏板宽为30cm,一个台阶的高度为15cm,求楼梯倾斜角的正切值。
⑵如图,在Rt△ABC中,∠C=90°,AB=5,BC=,求tanA与tanB的值。
⑶如图,在Rt△ABC中,∠C=90°,BC=12,tanA=,求AB的值。
B级:
⑴如图,在在Rt△ABC中,∠ACB=90°,CD是AB边上的高,
①tanA= = ;
②tanB= = ;
③tan∠ACD= ;
④tan∠BCD= ;
⑵如图,身高为1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m ,CA=0.8m,
求树的高度是多少?
C级:
⑶如图4,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,求路灯A的高AB。
B
A
A′
B′
C
D
A
C
B
E
A
B
B1
B2
C
C1
C2
A
B
C
a
b
A
B
C
3
4
A
B
C
B
A
C
A
B
C
D
A
B
C
D
E
F
PAGE
3
学习过程:
问题的提出
⑴如图,一把梯子斜靠在墙上,当它的顶端向下滑动后,它的底端将如何运动?滑动前(图中AB)与滑动后(图中A′B′)的位置的梯子,哪一个更陡些?你是根据什么判断的?你能用语言向同学描述吗?
⑵如何描述梯子在两个不同位置的具体的倾斜程度呢?
提示:在这一过程中变化的量有哪些?如何变化的?
⑶如图,如果两把梯子AB、CD靠在墙上,且AB∥CD,
这两把梯子的倾斜程度相同吗?前面所提到的描述倾斜
程度的量在这里分别对应相同吗?你能说明理由吗?
问题的发展
一般地,如果锐角A的大小确定,我们可以作出无数个以A为一个锐角直角三形(如图),那么图中:成立吗?
⑴当∠A变化时,上面等式仍然成立吗?
⑵上面等式的值随∠A的变化而变化吗?
概念的形成
由前面的探索可以看出:如果一个直角三角形的一个锐角的大小确定,那么这个锐角的对边与这个角的邻边的比值也确定。
这个比值反映了斜边相对于这角的邻边的倾斜程度,它与这个锐角的大小有着密切的关系。
在直角三角形中,我们将∠A的对边与它的邻边的比称为∠A的正切,记作 tanA即:
4.一个锐角的正切值
⑴如图,△ABC中,AC=4,BC=3,∠C=90°,求:tanA与 tanB的值。
⑵你能用画图的方法计算一个50°角的正切的近似值吗?
据图填表:
0°
20°
30°
45°
55°
65°
75°
⑶如图,从点O出发,点P沿65°线移动,当在水平方向上向右前进了一个单位时,它在垂直方向上向上前进了 个单位。P点的坐标是 ,tan65°≈ 。
①想一想:锐角的正切值是如何随着的变化而变化的?
②关于用计算器计算正切值请课后自学。
三.巩固与拓展
A级:
⑴某楼梯的踏板宽为30cm,一个台阶的高度为15cm,求楼梯倾斜角的正切值。
⑵如图,在Rt△ABC中,∠C=90°,AB=5,BC=,求tanA与tanB的值。
⑶如图,在Rt△ABC中,∠C=90°,BC=12,tanA=,求AB的值。
B级:
⑴如图,在在Rt△ABC中,∠ACB=90°,CD是AB边上的高,
①tanA= = ;
②tanB= = ;
③tan∠ACD= ;
④tan∠BCD= ;
⑵如图,身高为1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m ,CA=0.8m,
求树的高度是多少?
C级:
⑶如图4,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,求路灯A的高AB。
B
A
A′
B′
C
D
A
C
B
E
A
B
B1
B2
C
C1
C2
A
B
C
a
b
A
B
C
3
4
A
B
C
B
A
C
A
B
C
D
A
B
C
D
E
F
PAGE
3
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
