人教版八年级数学上册--11.1.1三角形的边-教学设计(表格式)
文档属性
| 名称 | 人教版八年级数学上册--11.1.1三角形的边-教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 78.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-16 22:45:30 | ||
图片预览


文档简介
教 学 设 计
课题 三角形的边 备课时间
授课教师 单 位
教 材 分 析 本节课是中考总复习三角形的第一讲, 主要复习三角形的基本概念和基本定理
学 情 分 析 三角形在平时应用较频繁,知识较熟悉,但应用不熟练。
教学目标 立足教材,打好基础,查漏补缺,系统复习,熟练掌握本部分的基本知识、基本方法和基本技能. 让学生自己总结交流所学内容,发展学生的语言表达能力和合作交流能力. 通过学生自己归纳总结本部分内容,使他们在动手操作方面,探索研究方面,语言表达方面,分类讨论、归纳等方面都有所发展.
教学重点
教学难点 把实际问题归结为解直角三角形问题。
教法学法
设 计 思 路 通过解直角三角形的有关知识解决实际问题的关键是借助图形,将实际问题转化成为解直角三角形的问题,并分析题中的数量关系,将其归结为直角三角形中元素之间的关系。引导学生画出示意图,将实际问题的数量关系在图形中反映出来,把数和形结合起来,提高学生分析问题和解决问题的能力
教学准备 教师准备:多媒体,三角板,圆规 学生准备:圆规,三角板
教学过程 设计意图
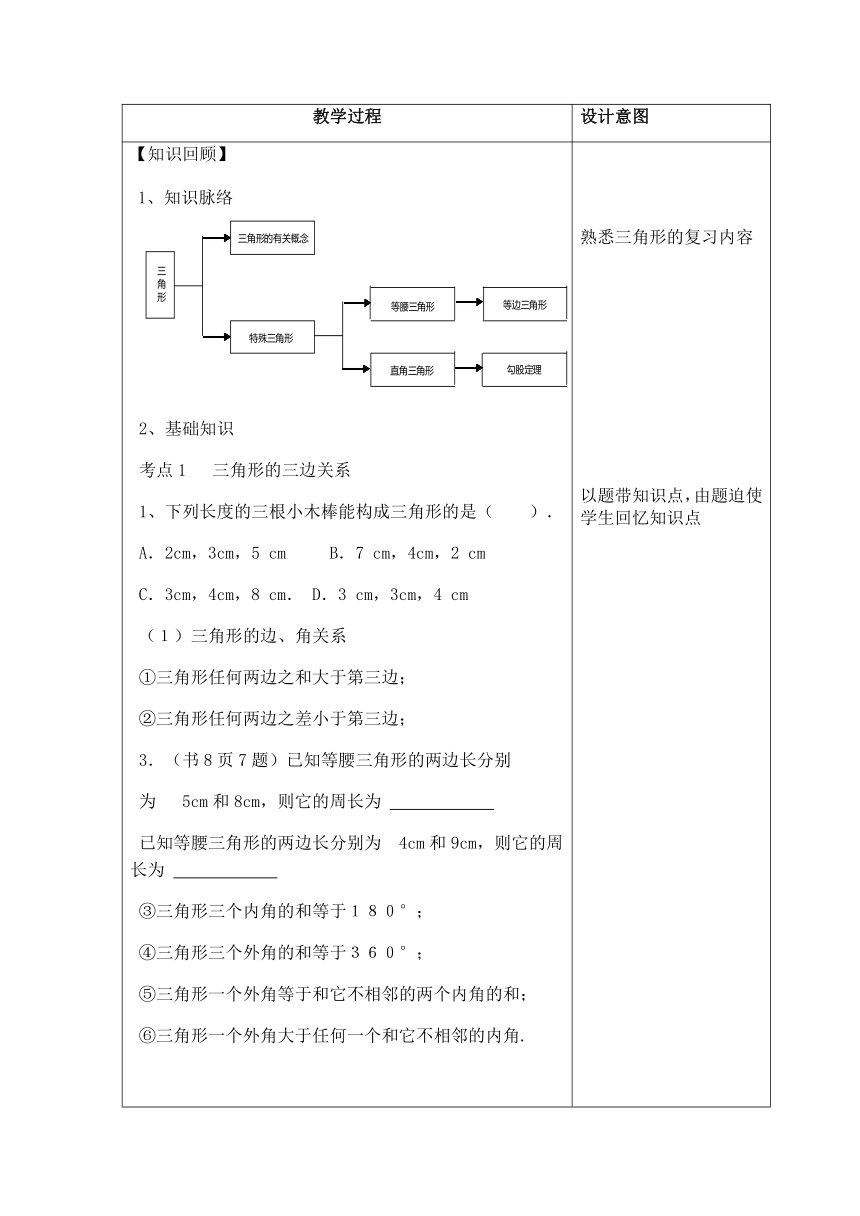
【知识回顾】 知识脉络 2、基础知识 考点1 三角形的三边关系 1、下列长度的三根小木棒能构成三角形的是( ). A.2cm,3cm,5 cm B.7 cm,4cm,2 cm C.3cm,4cm,8 cm. D.3 cm,3cm,4 cm (1)三角形的边、角关系 ①三角形任何两边之和大于第三边; ②三角形任何两边之差小于第三边; 3.(书8页7题)已知等腰三角形的两边长分别 为 5cm和8cm,则它的周长为 已知等腰三角形的两边长分别为 4cm和9cm,则它的周长为 ③三角形三个内角的和等于180°; ④三角形三个外角的和等于360°; ⑤三角形一个外角等于和它不相邻的两个内角的和; ⑥三角形一个外角大于任何一个和它不相邻的内角. 考点2 三角形的角的关系 4、(2015·滨州)在△ABC中,∠A:∠B:∠C =2:3:5,则∠C= . 考点3三角形的重要线段 6、在△ABC中,AD和AE分别是边BC上的中线和高,AB=3 cm,AC=2cm,S△ABD=1.5cm2,则S△ACD为 △ABD的 周长与△ADC的周长差为 。 7、如图,△ABC中,若∠A=80°,∠ABC和∠ACB的平分线交于点O,则∠BOC= . (2)三角形的主要线段和外心、内心 ①三角形的角平分线、中线、高; ②三角形三边的垂直平分线交于一点,这个点叫做三角形的外心,三角形的外心到各顶点的距离相等; ③三角形三条角平分线交于一点,这个点叫做三角形的内心,三角形的内心到三边的距离相等; 考点4 三角形的中位线定理 8、如图,已知四边形ABCD,R,P分别是DC,BC上的点, E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动而点R不动时,那么下列结论成立的是( ) A.线段EF的长逐渐增大 B.线段EF的长逐渐减少 C.线段EF的长不变 D.线段EF的长不能确定 ④连结三角形两边中点的线段叫做三角形的中位线,三角形的中位线平行于第三边且等于第三边的一半. 能力提升 9、三角形两边长分别是3和6,第三边的长是方 程x2-13x+36=0的根,则三角形的周长为( ) A、13 B、15 C、18 D、13或18 10、(2016年·石家庄一模)在△ABC中,AB=AC,D 为BC上的一点,CD=AD,AB=BD,则∠C的度数是( ) (
A
)A、30° B、36° C、40° D、45° (
C
) (
D
) (
B
) 11、(2016北京)如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN (1)求证:BM=MN (
A
)(2)若∠BAD=60°,AC平分∠BAD,AC=2,求BN得长。 (
M
) (
N
) (
D
) (
C
) (
B
) 12、(2016·贵阳)(1)阅读理解:如图①,在△ABC中, 若AB=10,AC=6,求BC边上的中线AD的取值范围. 解决此 问题可以用如下方法: 延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆 时针旋转180°得到△EBD),把AB、AC,2AD集中在△A BE中,利用三角形三边的关系即可判断. 中线AD的取值范围是 ; (2)问题解决: 如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D, DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF; 熟悉三角形的复习内容 以题带知识点,由题迫使学生回忆知识点
【板书设计】28.2应用举例 1、三角形的三边关系 学生板演 2、三角形的角的关系 3、三角形的重要线段 4、三角形的中位线定理 例题板演
课后反思 课堂容量小 教师说的多
点评
课题 三角形的边 备课时间
授课教师 单 位
教 材 分 析 本节课是中考总复习三角形的第一讲, 主要复习三角形的基本概念和基本定理
学 情 分 析 三角形在平时应用较频繁,知识较熟悉,但应用不熟练。
教学目标 立足教材,打好基础,查漏补缺,系统复习,熟练掌握本部分的基本知识、基本方法和基本技能. 让学生自己总结交流所学内容,发展学生的语言表达能力和合作交流能力. 通过学生自己归纳总结本部分内容,使他们在动手操作方面,探索研究方面,语言表达方面,分类讨论、归纳等方面都有所发展.
教学重点
教学难点 把实际问题归结为解直角三角形问题。
教法学法
设 计 思 路 通过解直角三角形的有关知识解决实际问题的关键是借助图形,将实际问题转化成为解直角三角形的问题,并分析题中的数量关系,将其归结为直角三角形中元素之间的关系。引导学生画出示意图,将实际问题的数量关系在图形中反映出来,把数和形结合起来,提高学生分析问题和解决问题的能力
教学准备 教师准备:多媒体,三角板,圆规 学生准备:圆规,三角板
教学过程 设计意图
【知识回顾】 知识脉络 2、基础知识 考点1 三角形的三边关系 1、下列长度的三根小木棒能构成三角形的是( ). A.2cm,3cm,5 cm B.7 cm,4cm,2 cm C.3cm,4cm,8 cm. D.3 cm,3cm,4 cm (1)三角形的边、角关系 ①三角形任何两边之和大于第三边; ②三角形任何两边之差小于第三边; 3.(书8页7题)已知等腰三角形的两边长分别 为 5cm和8cm,则它的周长为 已知等腰三角形的两边长分别为 4cm和9cm,则它的周长为 ③三角形三个内角的和等于180°; ④三角形三个外角的和等于360°; ⑤三角形一个外角等于和它不相邻的两个内角的和; ⑥三角形一个外角大于任何一个和它不相邻的内角. 考点2 三角形的角的关系 4、(2015·滨州)在△ABC中,∠A:∠B:∠C =2:3:5,则∠C= . 考点3三角形的重要线段 6、在△ABC中,AD和AE分别是边BC上的中线和高,AB=3 cm,AC=2cm,S△ABD=1.5cm2,则S△ACD为 △ABD的 周长与△ADC的周长差为 。 7、如图,△ABC中,若∠A=80°,∠ABC和∠ACB的平分线交于点O,则∠BOC= . (2)三角形的主要线段和外心、内心 ①三角形的角平分线、中线、高; ②三角形三边的垂直平分线交于一点,这个点叫做三角形的外心,三角形的外心到各顶点的距离相等; ③三角形三条角平分线交于一点,这个点叫做三角形的内心,三角形的内心到三边的距离相等; 考点4 三角形的中位线定理 8、如图,已知四边形ABCD,R,P分别是DC,BC上的点, E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动而点R不动时,那么下列结论成立的是( ) A.线段EF的长逐渐增大 B.线段EF的长逐渐减少 C.线段EF的长不变 D.线段EF的长不能确定 ④连结三角形两边中点的线段叫做三角形的中位线,三角形的中位线平行于第三边且等于第三边的一半. 能力提升 9、三角形两边长分别是3和6,第三边的长是方 程x2-13x+36=0的根,则三角形的周长为( ) A、13 B、15 C、18 D、13或18 10、(2016年·石家庄一模)在△ABC中,AB=AC,D 为BC上的一点,CD=AD,AB=BD,则∠C的度数是( ) (
A
)A、30° B、36° C、40° D、45° (
C
) (
D
) (
B
) 11、(2016北京)如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN (1)求证:BM=MN (
A
)(2)若∠BAD=60°,AC平分∠BAD,AC=2,求BN得长。 (
M
) (
N
) (
D
) (
C
) (
B
) 12、(2016·贵阳)(1)阅读理解:如图①,在△ABC中, 若AB=10,AC=6,求BC边上的中线AD的取值范围. 解决此 问题可以用如下方法: 延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆 时针旋转180°得到△EBD),把AB、AC,2AD集中在△A BE中,利用三角形三边的关系即可判断. 中线AD的取值范围是 ; (2)问题解决: 如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D, DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF; 熟悉三角形的复习内容 以题带知识点,由题迫使学生回忆知识点
【板书设计】28.2应用举例 1、三角形的三边关系 学生板演 2、三角形的角的关系 3、三角形的重要线段 4、三角形的中位线定理 例题板演
课后反思 课堂容量小 教师说的多
点评
