2.3 直线的参数方程 课件(共19张PPT)
文档属性
| 名称 | 2.3 直线的参数方程 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-14 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
2.3.1 直线的参数方程
高中数学选修4-4
1.直线的方向向量的概念.
2.在平面直角坐标系中,确定一条直线的几何条件是什么?
3.已知一条直线的倾斜角和所过的一个定点,请写出直线的方程.
4.如何建立直线的参数方程?
回忆旧知,课题导入:
问题情景:
这推导过程中α≠0°且α≠90°
那一般直线参数方程怎么求呢?
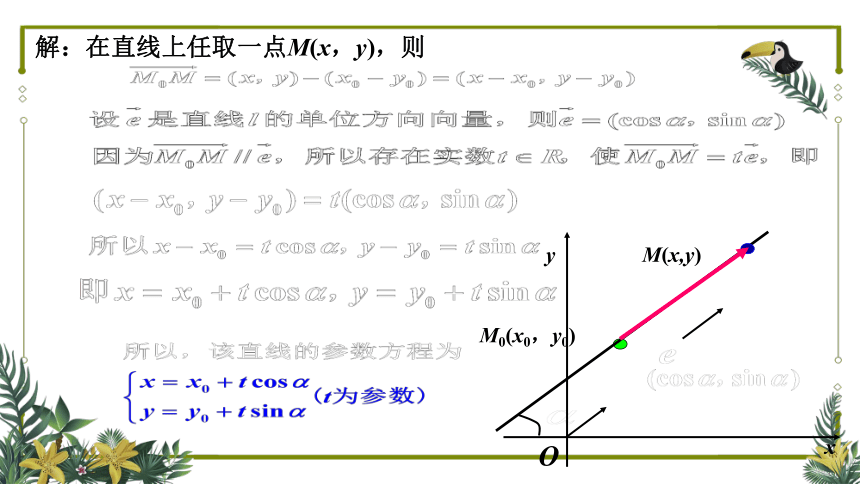
M0(x0,y0)
M(x,y)
解:在直线上任取一点M(x,y),则
x
O
y
探究思考(一):
| t | = | M0M |
M0
M
所以,直线参数方程中参数t的绝对值等于直线上动点M到定点M0的距离.
这就是 t 的几何意义,要牢记
x
O
y
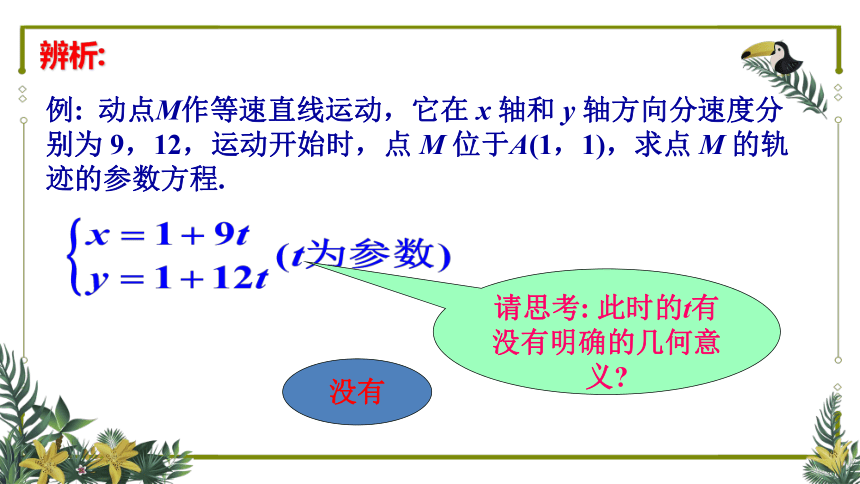
辨析:
例: 动点M作等速直线运动,它在 x 轴和 y 轴方向分速度分别为 9,12,运动开始时,点 M 位于A(1,1),求点 M 的轨迹的参数方程.
请思考: 此时的t有没有明确的几何意义
没有
分析:
3.点M是否在直线上
1.用普通方程去解还是用参数方程去解;
2.分别如何解.
A
B
M(-1,2)
x
y
O
知识能力提升:
解:因为把点M的坐标代入直线方程后,符合直线方程,所以点M在直线上.
M(-1,2)
A
B
x
O
y
M(-1,2)
A
B
x
O
y
探究思考(二):
课堂检测:
已知过点
,斜率为
的直线和抛物线
相交于A,B两点,设线段AB的中点为M,求点M的坐标.
课堂小结:
1.知识小结
本节课联系数轴、向量等知识,推导出了直线的参数方程,并进行了简单应用,体会了直线参数方程在解决有关问题时的作用.
2.思想方法小结
在研究直线参数方程过程中渗透了运动与变化、类比、数形结合、转化等数学思想.
谢谢观看!
2.3.1 直线的参数方程
高中数学选修4-4
1.直线的方向向量的概念.
2.在平面直角坐标系中,确定一条直线的几何条件是什么?
3.已知一条直线的倾斜角和所过的一个定点,请写出直线的方程.
4.如何建立直线的参数方程?
回忆旧知,课题导入:
问题情景:
这推导过程中α≠0°且α≠90°
那一般直线参数方程怎么求呢?
M0(x0,y0)
M(x,y)
解:在直线上任取一点M(x,y),则
x
O
y
探究思考(一):
| t | = | M0M |
M0
M
所以,直线参数方程中参数t的绝对值等于直线上动点M到定点M0的距离.
这就是 t 的几何意义,要牢记
x
O
y
辨析:
例: 动点M作等速直线运动,它在 x 轴和 y 轴方向分速度分别为 9,12,运动开始时,点 M 位于A(1,1),求点 M 的轨迹的参数方程.
请思考: 此时的t有没有明确的几何意义
没有
分析:
3.点M是否在直线上
1.用普通方程去解还是用参数方程去解;
2.分别如何解.
A
B
M(-1,2)
x
y
O
知识能力提升:
解:因为把点M的坐标代入直线方程后,符合直线方程,所以点M在直线上.
M(-1,2)
A
B
x
O
y
M(-1,2)
A
B
x
O
y
探究思考(二):
课堂检测:
已知过点
,斜率为
的直线和抛物线
相交于A,B两点,设线段AB的中点为M,求点M的坐标.
课堂小结:
1.知识小结
本节课联系数轴、向量等知识,推导出了直线的参数方程,并进行了简单应用,体会了直线参数方程在解决有关问题时的作用.
2.思想方法小结
在研究直线参数方程过程中渗透了运动与变化、类比、数形结合、转化等数学思想.
谢谢观看!
