椭圆的离心率课件-2021-2022学年高二上学期数学人教A版选修1-1(24张PPT)
文档属性
| 名称 | 椭圆的离心率课件-2021-2022学年高二上学期数学人教A版选修1-1(24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-15 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
椭圆的离心率
一、椭圆的离心率
o
x
y
离心率:椭圆的焦距与长轴长的比,
,∴0(2)e越接近1,椭圆越扁;
e越接近于0,椭圆越接近于圆.
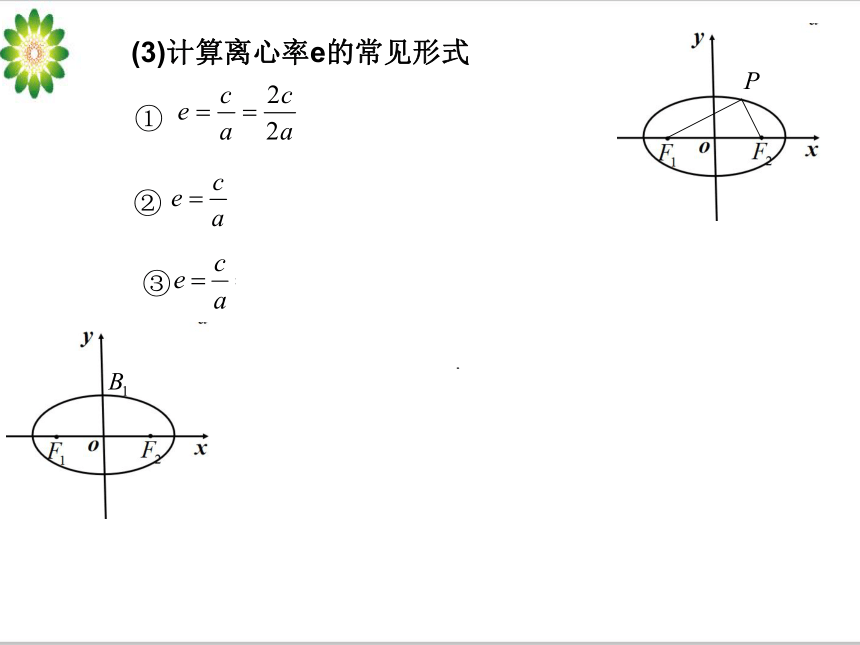
(3)计算离心率e的常见形式
①
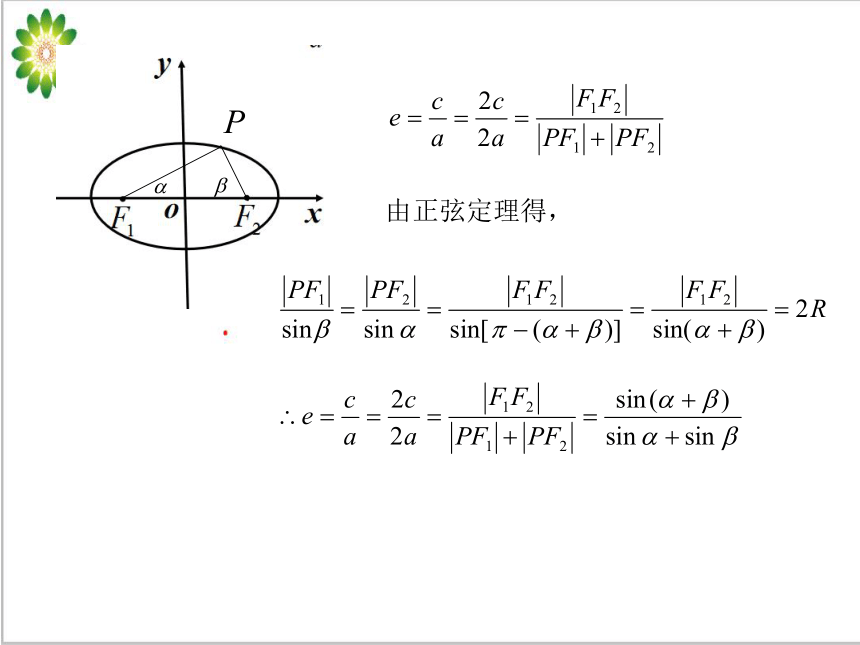
⑤在焦点三角形中,
②
③
④在特征三角形中,
(3)计算离心率e的常见形式
①
⑤在焦点三角形中,
②
③
④在特征三角形中,
小结论(二级):
(1)椭圆的通径
过椭圆的焦点且垂直于长轴长的直线被椭圆截得的弦成为椭圆的通径
(2)
例2-1
上的一点,
例2-2
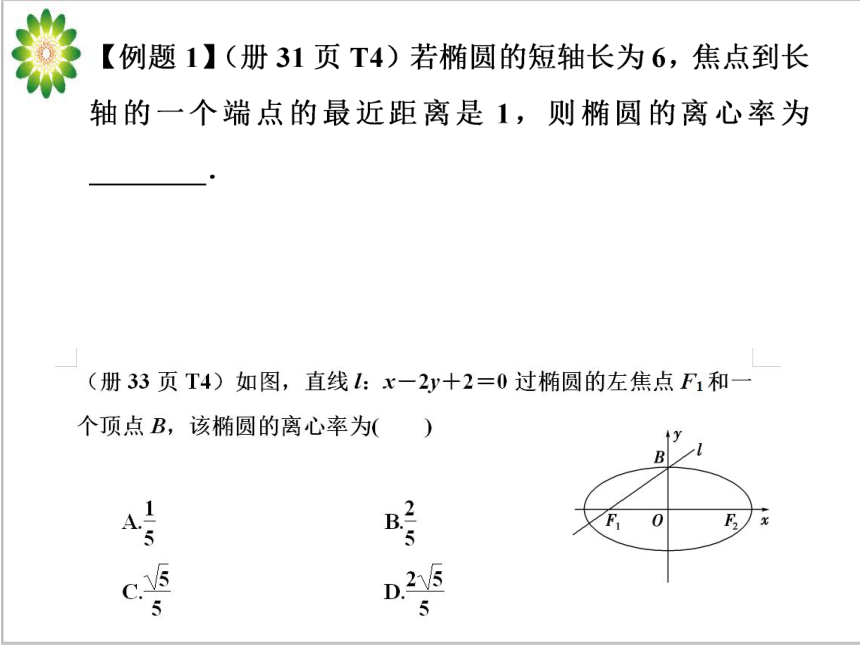
(高考真题:直线 经过椭圆的一个顶点和一个焦点,若椭圆
中心到 的距离为其短轴长的 ,则该椭圆的离心率为
一
二
例2-3
若椭圆恰好平分正三角形的另两边,则椭圆的离心率为 。
为边做正三角形,
例2-4
册34页B组2
例2-5
例2-6
例3:(1)若一个椭圆长轴的长度、短轴的长度和焦距成等差数列,则该椭圆的离心率为 ;
(2)若椭圆的通径与该椭圆中心所成的角为直角,则该椭圆离心率e=
练习1.已知椭圆方程为6x2+y2=6
它的长轴长是: .短轴长是: .
焦距是: . 离心率等于: .
焦点坐标是: . 顶点坐标是: .
外切矩形的面积等于: .
练习2.若椭圆 的
离心率 ,则 m = .
说明:要分焦点在 轴和 轴两种情况!
2
或8
练习3.若椭圆短轴一端点到椭圆一焦点的距离是该焦点到同侧长轴一端点距离的3倍,则椭圆的离心率=
X
Y
O
F
练习4.若椭圆的长轴长不大于短轴长的2倍,则椭圆的离心率 .
标准方程
图 象
范 围
对 称 性
顶点坐标
焦点坐标
半 轴 长
焦 距
a,b,c关系
离 心 率
|x|≤ a,|y|≤ b
|x|≤ b,|y|≤ a
( a ,0 ),(0, b)
( b ,0 ),(0, a)
( c,0)
(0, c)
长半轴长为a,
短半轴长为b.
焦距为2c;
a2=b2+c2
练习5小结
关于x轴、y轴成轴对称;
关于原点成中心对称。
关于x轴、y轴成轴对称;
关于原点成中心对称。
长半轴长为a,
短半轴长为b.
焦距为2c;
a2=b2+c2
讨论6:
焦点在y轴的情况又如何?
x
y
x
y
讨论5:
那 变化对椭圆的影响又是什么?
探究四、椭圆的离心率
代数变形:
探究:(教材P40)
1. 的大小能刻画椭圆的扁平程度吗?
为什么?
2.你能运用三角函数的知识解释为什么
越大,椭圆越扁? 越小,椭圆越圆吗?
课后作业1.
椭圆的离心率
一、椭圆的离心率
o
x
y
离心率:椭圆的焦距与长轴长的比,
,∴0
e越接近于0,椭圆越接近于圆.
(3)计算离心率e的常见形式
①
⑤在焦点三角形中,
②
③
④在特征三角形中,
(3)计算离心率e的常见形式
①
⑤在焦点三角形中,
②
③
④在特征三角形中,
小结论(二级):
(1)椭圆的通径
过椭圆的焦点且垂直于长轴长的直线被椭圆截得的弦成为椭圆的通径
(2)
例2-1
上的一点,
例2-2
(高考真题:直线 经过椭圆的一个顶点和一个焦点,若椭圆
中心到 的距离为其短轴长的 ,则该椭圆的离心率为
一
二
例2-3
若椭圆恰好平分正三角形的另两边,则椭圆的离心率为 。
为边做正三角形,
例2-4
册34页B组2
例2-5
例2-6
例3:(1)若一个椭圆长轴的长度、短轴的长度和焦距成等差数列,则该椭圆的离心率为 ;
(2)若椭圆的通径与该椭圆中心所成的角为直角,则该椭圆离心率e=
练习1.已知椭圆方程为6x2+y2=6
它的长轴长是: .短轴长是: .
焦距是: . 离心率等于: .
焦点坐标是: . 顶点坐标是: .
外切矩形的面积等于: .
练习2.若椭圆 的
离心率 ,则 m = .
说明:要分焦点在 轴和 轴两种情况!
2
或8
练习3.若椭圆短轴一端点到椭圆一焦点的距离是该焦点到同侧长轴一端点距离的3倍,则椭圆的离心率=
X
Y
O
F
练习4.若椭圆的长轴长不大于短轴长的2倍,则椭圆的离心率 .
标准方程
图 象
范 围
对 称 性
顶点坐标
焦点坐标
半 轴 长
焦 距
a,b,c关系
离 心 率
|x|≤ a,|y|≤ b
|x|≤ b,|y|≤ a
( a ,0 ),(0, b)
( b ,0 ),(0, a)
( c,0)
(0, c)
长半轴长为a,
短半轴长为b.
焦距为2c;
a2=b2+c2
练习5小结
关于x轴、y轴成轴对称;
关于原点成中心对称。
关于x轴、y轴成轴对称;
关于原点成中心对称。
长半轴长为a,
短半轴长为b.
焦距为2c;
a2=b2+c2
讨论6:
焦点在y轴的情况又如何?
x
y
x
y
讨论5:
那 变化对椭圆的影响又是什么?
探究四、椭圆的离心率
代数变形:
探究:(教材P40)
1. 的大小能刻画椭圆的扁平程度吗?
为什么?
2.你能运用三角函数的知识解释为什么
越大,椭圆越扁? 越小,椭圆越圆吗?
课后作业1.
