5.1 平行四边形的性质 同步练习(含解析)
文档属性
| 名称 | 5.1 平行四边形的性质 同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 09:37:07 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第五章 平行四边形
1 平行四边形的性质
基础过关
知识点1 平行四边形的定义
1.如图,AC∥HD∥GE,AG∥BF∥CE,则平行四边形一共有( )
A.7个 B.8个 C.9个 D.10个
知识点2 平行四边形的性质
2.已知平行四边形ABCD中,∠A+∠C=110°,则∠B的度数为( )
A.125° B.135° C.145° D.155°
3.如图,在平行四边形ABCD中,DE平分∠ADC,AD=8,BE=3,则CD=( )
A.4 B.5 C.6 D.7
4.已知平行四边形ABCD的周长为26cm,对角线AC、BD相交于点O,若△BOC的周长比△AOB的周长多3cm,则BC的长度为( )
A.5 cm B.6 cm C.7 cm D.8 cm
5.如图,在平行四边形ABCD中,DE平分∠ADC,交BC于点E,AF⊥DE,若∠DAF=50°,则∠C的度数是( )
A.100° B.80° C.70° D.110°
6.如图所示,在平行四边形ABCD中,M是CD的中点,AB=2BC,BM=1,AM=2,则CD的长为( )
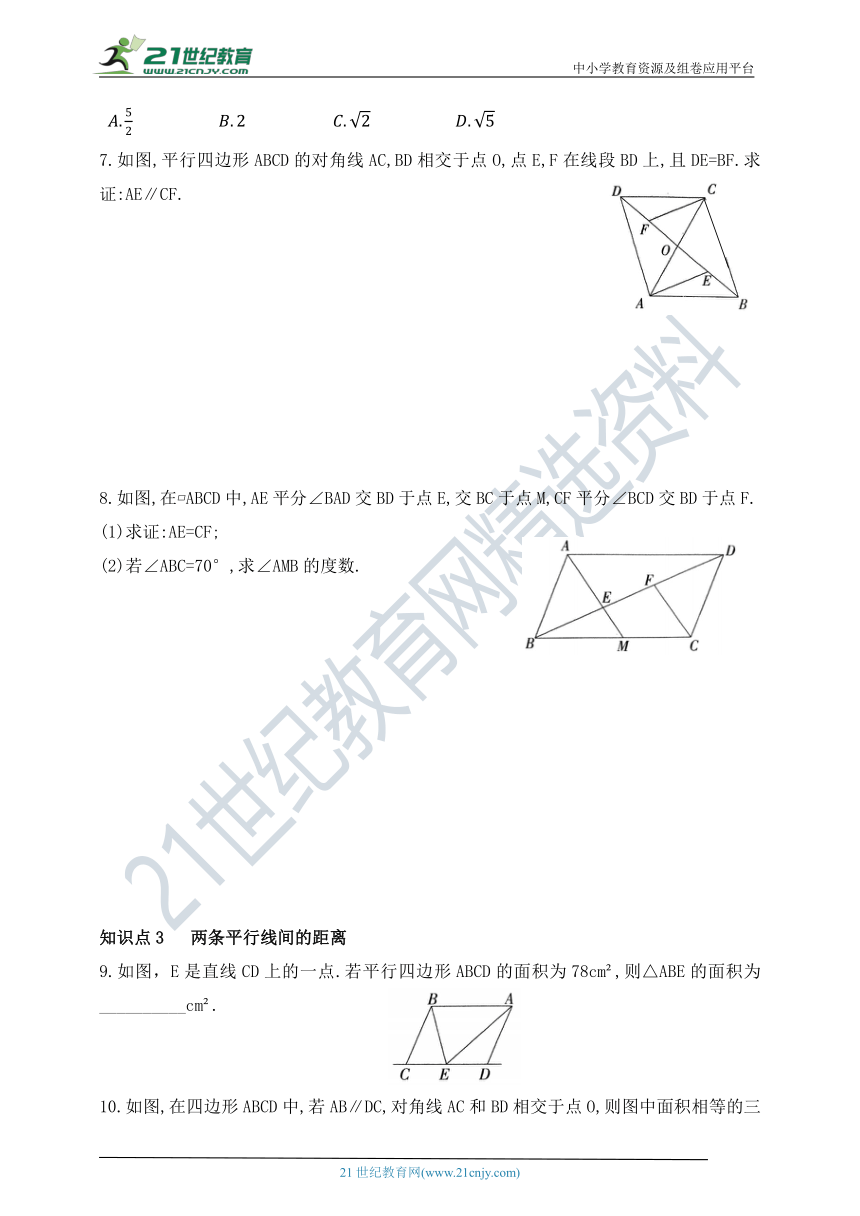
7.如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F在线段BD上,且DE=BF.求证:AE∥CF.
8.如图,在 ABCD中,AE平分∠BAD交BD于点E,交BC于点M,CF平分∠BCD交BD于点F.
(1)求证:AE=CF;
(2)若∠ABC=70°,求∠AMB的度数.
知识点3 两条平行线间的距离
9.如图,E是直线CD上的一点.若平行四边形ABCD的面积为78cm ,则△ABE的面积为__________cm .
10.如图,在四边形ABCD中,若AB∥DC,对角线AC和BD相交于点O,则图中面积相等的三角形有__________对.
能力提升
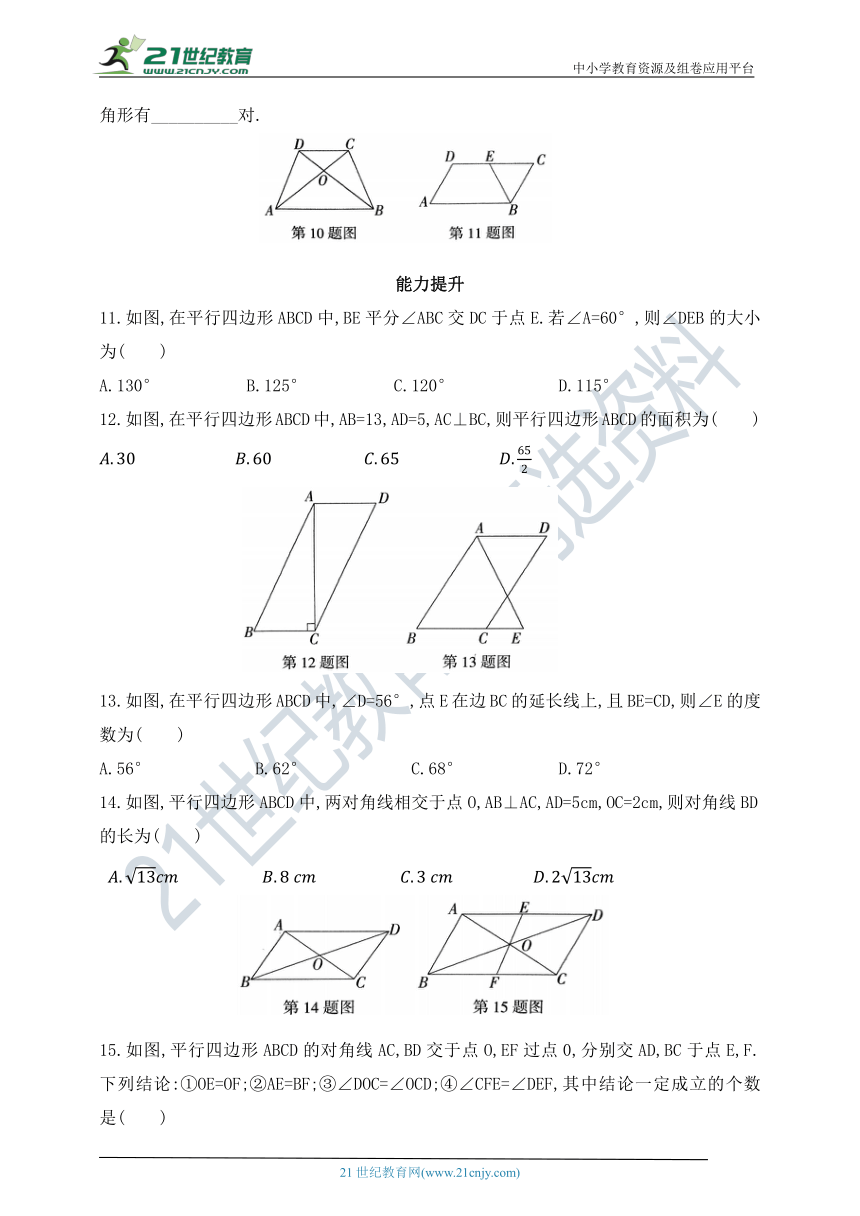
11.如图,在平行四边形ABCD中,BE平分∠ABC交DC于点E.若∠A=60°,则∠DEB的大小为( )
A.130° B.125° C.120° D.115°
12.如图,在平行四边形ABCD中,AB=13,AD=5,AC⊥BC,则平行四边形ABCD的面积为( )
13.如图,在平行四边形ABCD中,∠D=56°,点E在边BC的延长线上,且BE=CD,则∠E的度数为( )
A.56° B.62° C.68° D.72°
14.如图,平行四边形ABCD中,两对角线相交于点O,AB⊥AC,AD=5cm,OC=2cm,则对角线BD的长为( )
15.如图,平行四边形ABCD的对角线AC,BD交于点O,EF过点0,分别交AD,BC于点E,F.下列结论:①OE=OF;②AE=BF;③∠DOC=∠OCD;④∠CFE=∠DEF,其中结论一定成立的个数是( )
A.1 B.2 C.3 D.4
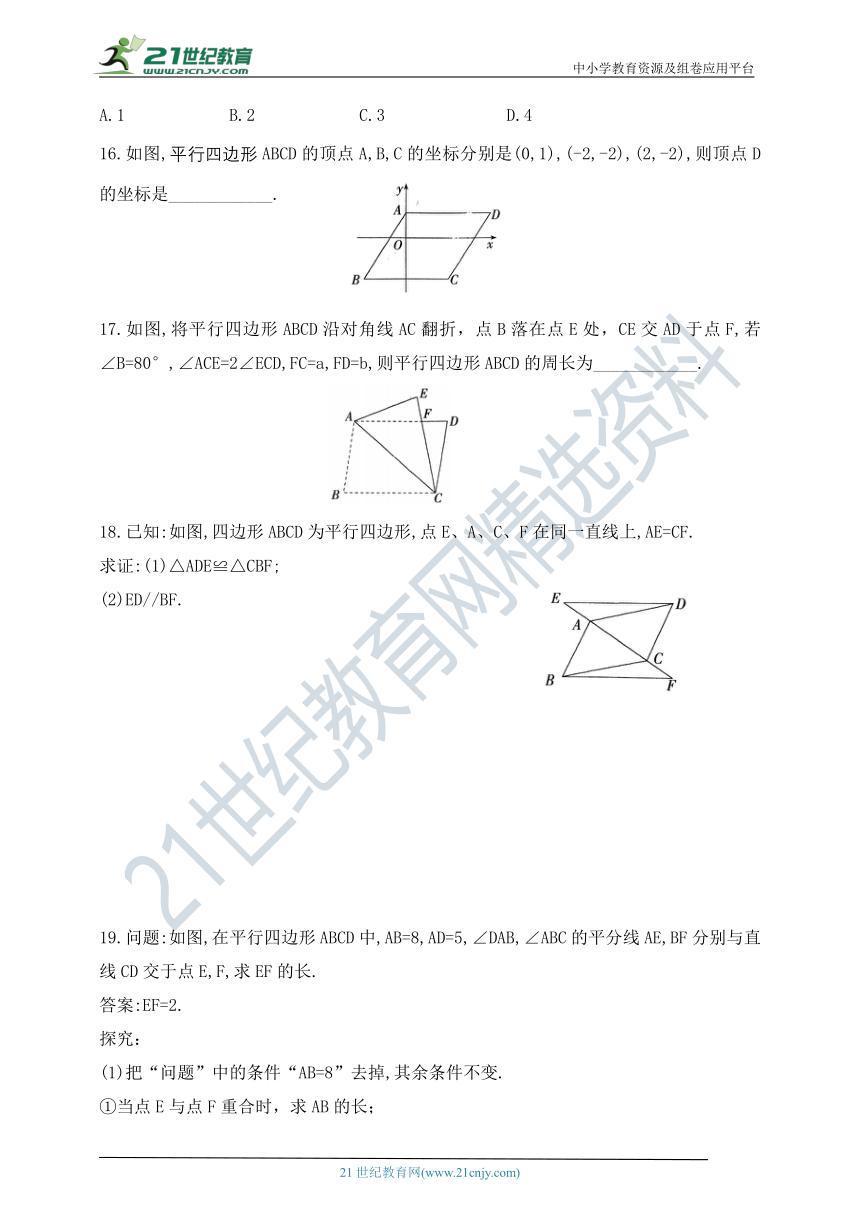
16.如图,平行四边形ABCD的顶点A,B,C的坐标分别是(0,1),(-2,-2),(2,-2),则顶点D的坐标是____________.
17.如图,将平行四边形ABCD沿对角线AC翻折,点B落在点E处,CE交AD于点F,若∠B=80°,∠ACE=2∠ECD,FC=a,FD=b,则平行四边形ABCD的周长为____________.
18.已知:如图,四边形ABCD为平行四边形,点E、A、C、F在同一直线上,AE=CF.
求证:(1)△ADE≌△CBF;
(2)ED//BF.
19.问题:如图,在平行四边形ABCD中,AB=8,AD=5,∠DAB,∠ABC的平分线AE,BF分别与直线CD交于点E,F,求EF的长.
答案:EF=2.
探究:
(1)把“问题”中的条件“AB=8”去掉,其余条件不变.
①当点E与点F重合时,求AB的长;
②当点E与点C重合时,求EF的长.
(2)把“问题”中的条件“AB=8,AD=5”去掉,其余条件不变,当D,F,E,C相邻两点间的距离相等时,求 的值.
20.[直观想象、逻辑推理]如图①,在平行四边形ABCD中,对角线AC、BD相交于点O,过O点作直线EF,分别交BC、AD于点E、F.
(1)证明:OF=OE;
(2)小明从图①中找到了一种将平行四边形的面积平分的方法.图②是一块纸片,其形状是一个大的平行四边形在一角剪去一个小的平行四边形,小明发现可以用一条直线将纸片分割成面积相等的两部分,请你帮助小明设计三种不同的分割方案.
参考答案
基础过关
1.C ∵AC∥HD∥GE,AG∥BF∥CE,∴四边形AHOB、四边形HGFO、四边形BODC、四边形OFED、四边形AGFB、四边形BFEC、四边形AHDC、四边形HGED、四边形AGEC都是平行四边形,共9个,故选C.
2.A 因为四边形ABCD为平行四边形,∠A+∠C=110°,所以∠A=∠C=55°,AD∥BC,所以∠A+∠B=180°,所以∠B=180°-∠A=125°,故选A.
3.B ∵四边形ABCD为平行四边形,AD=8,∴BC=AD=8,AD∥BC,
∴CE=BC-BE=8-3=5,∠ADE=∠CED,
∵DE平分∠ADC,∴∠ADE=∠CDE,∴∠CDE=∠CED,∴CD=CE=5,故选B.
4.D ∵四边形ABCD为平行四边形,且周长为26cm,∴AB+BC=13cm,OA=OC,
∵△BOC的周长比△AOB的周长多3cm,∴(OB+OC+BC)-(OA+OB+AB)=BC-AB=3 cm,
∴AB=5cm,BC=8 cm.故选D.
5.A 因为AF⊥DE,所以∠AFD=90°,所以∠ADF=90°-∠DAF=40°,因为DE平分∠ADC,所以∠ADC=2∠ADF=80°,因为四边形ABCD是平行四边形,所以AD∥BC,所以∠C+∠ADC=180°,所以∠C=180°-∠ADC=100°.
6.D 在平行四边形ABCD中,AD=BC,CD=AB.
∵M为CD的中点,AB=2BC,
∴∠DAM=∠DMA,∠CBM=∠CMB,
∵∠C+∠D=180°,∠C+∠CMB+∠CBM=180°,∠D+∠DAM+∠DMA=180°,
∴∠C=2∠DMA,∠D=2∠CMB,
∴∠AMB=180°-(∠DMA+∠CMB)=90°,即△MAB为直角三角形,
故选D.
7.证明 ∵四边形ABCD是平行四边形,
∴AD=CB,AD∥BC,∴∠ADE=∠CBF,
在△ADE和△CBF中∴△ADE≌△CBF(SAS),
∴∠AED=∠CFB,∴AE∥CF.
8.解析 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∠BAD=∠BCD,∴∠ABE=∠CDF,
∵AE平分∠BAD,CF平分∠BCD,
∴∠BAE=∠DCF,∴△ABE≌△CDF(ASA),∴AE=CF.
(2)∵四边形ABCD是平行四边形,∴AD∥BC,∠BAD+∠ABC=180°,
∵∠ABC=70°,∴∠BAD=110°,
∵AM平分∠BAD,AD∥BC,∴∠DAM=∠BAM=55°,∠DAM=∠AMB,∴∠AMB=55°.
9.答案 39
解析 如图,分别过点D、E作直线AB的垂线,垂足为F、G,∴ DF∥EG.
∵四边形ABCD为平行四边形,∴AB∥DC,∴DF=EG,
10.答案 3
解析 由题意可知,△ADC与△BCD的面积相等,△ADB与△BCA的面积相等,△ADO与△BCO的面积相等,共有3对.
能力提升
11.C ∵四边形ABCD是平行四边形,∴AD∥BC,DC∥AB,
∴∠A+∠ABC=180°,∠ABE+∠DEB=180°,
∵∠A=60°,∴∠ABC=120°,
∵BE平分∠ABC,∴∠ABE=60°,
∴∠DEB=180°-60°=120°,故选C.
12.B ∵四边形ABCD为平行四边形,∴BC=AD=5.
∵AC⊥BC,∴△ACB是直角三角形.
故选B.
13.B ∵四边形ABCD是平行四边形,
∴AB=CD,∠B=∠D=56°,
∵BE=CD,∴ AB=BE,∴△ABE是等腰三角形,
故选B.
14.D ∵四边形ABCD为平行四边形,
∴BO=DO,AO=OC=2cm,BC=AD=5cm,∴AC=4cm,
∵AB⊥AC,∴∠BAO=90°,
在Rt△ABO中,由勾股定理得
故选D.
15.A ∵四边形ABCD为平行四边形,∴AO=CO,BO=DO,AD∥BC,∴∠EAO=∠FCO,
在△AOE和△COF中∴△AOE≌△COF(ASA),
∴OE=OF,AE=CF,∠CFE=∠AEF,∴①一定成立,②④不一定成立.③不一定成立,
故选A.
16.答案 (4,1)
解析 ∵点B,C的坐标分别是(-2,-2),(2,-2),∴BC=2-(-2)=2+2=4,
∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC=4,
∵点A的坐标为(0,1),∴点D的坐标为(4,1).
17.答案
解析 ∵四边形ABCD为平行四边形,∠B=80°,∴AD∥BC,∠D=80°.
由折叠可知∠ACB=∠ACE,又AD∥BC,∴∠DAC=∠ACB,∴∠ACE=∠DAC,
∴△AFC为等腰三角形.∴AF=FC=a.
设∠ECD=x,则∠ACE=2x,∴∠DAC=2x,
在△ADC中,由三角形内角和定理可知2x+2x+x+80°=180°,解得x=20°.
∴∠DFC=4x=80°,∴△DFC为等腰三角形.∴DC=FC=a.
∵AD=AF+FD=a+b,∴平行四边形ABCD的周长为2(DC+AD)=2(a+a+b)=4a+2b.
18.证明 (1)∵四边形ABCD为平行四边形,
∴DA=BC,DA∥BC,∴∠DAC=∠BCA,
∵∠DAC+∠EAD=180°,∠BCA+∠FCB=180°,∴∠EAD=∠FCB,
在△ADE和△CBF中∴△ADE≌△CBF(SAS).
(2)由(1)知△ADE≌△CBF,∴∠E=∠F,∴ED∥BF.
19.解析 (1)①如图所示:
∵四边形ABCD是平行四边形,∴CD=AB,BC=AD=5,AB∥CD,∴∠DEA=∠BAE,
∵AE平分∠DAB,∴∠DAE=∠BAE,∴∠DEA=∠DAE,∴DE=AD=5,同理CF=BC=5,
∵点E与点F重合,∴AB=CD=DE+CF=10.
②如图所示:
当点E与点C重合时,易得DE=AD=5,CF=BC=5,∴点F与点D重合,∴EF=AD=5.
(2)分三种情况:
①如图1所示:
易得AD=DE,
∵C,D,E,F相邻两点间的距离相等,
②如图2所示.
易得AD=DE=CF,DF=FE=CE,
③如图3所示:
易得AD=DE=CF,DF=DC=CE,
综上所述, 的值为 式 或2.
20.解析 (1)证明:∵四边形ABCD是平行四边形,∴AO=CO,AD∥BC,∴∠FAO=∠ECO.
在△AOF和△COE中∴△AOF≌△COE(ASA),∴OF=OE.
(2)如图所示:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 平行四边形
1 平行四边形的性质
基础过关
知识点1 平行四边形的定义
1.如图,AC∥HD∥GE,AG∥BF∥CE,则平行四边形一共有( )
A.7个 B.8个 C.9个 D.10个
知识点2 平行四边形的性质
2.已知平行四边形ABCD中,∠A+∠C=110°,则∠B的度数为( )
A.125° B.135° C.145° D.155°
3.如图,在平行四边形ABCD中,DE平分∠ADC,AD=8,BE=3,则CD=( )
A.4 B.5 C.6 D.7
4.已知平行四边形ABCD的周长为26cm,对角线AC、BD相交于点O,若△BOC的周长比△AOB的周长多3cm,则BC的长度为( )
A.5 cm B.6 cm C.7 cm D.8 cm
5.如图,在平行四边形ABCD中,DE平分∠ADC,交BC于点E,AF⊥DE,若∠DAF=50°,则∠C的度数是( )
A.100° B.80° C.70° D.110°
6.如图所示,在平行四边形ABCD中,M是CD的中点,AB=2BC,BM=1,AM=2,则CD的长为( )
7.如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F在线段BD上,且DE=BF.求证:AE∥CF.
8.如图,在 ABCD中,AE平分∠BAD交BD于点E,交BC于点M,CF平分∠BCD交BD于点F.
(1)求证:AE=CF;
(2)若∠ABC=70°,求∠AMB的度数.
知识点3 两条平行线间的距离
9.如图,E是直线CD上的一点.若平行四边形ABCD的面积为78cm ,则△ABE的面积为__________cm .
10.如图,在四边形ABCD中,若AB∥DC,对角线AC和BD相交于点O,则图中面积相等的三角形有__________对.
能力提升
11.如图,在平行四边形ABCD中,BE平分∠ABC交DC于点E.若∠A=60°,则∠DEB的大小为( )
A.130° B.125° C.120° D.115°
12.如图,在平行四边形ABCD中,AB=13,AD=5,AC⊥BC,则平行四边形ABCD的面积为( )
13.如图,在平行四边形ABCD中,∠D=56°,点E在边BC的延长线上,且BE=CD,则∠E的度数为( )
A.56° B.62° C.68° D.72°
14.如图,平行四边形ABCD中,两对角线相交于点O,AB⊥AC,AD=5cm,OC=2cm,则对角线BD的长为( )
15.如图,平行四边形ABCD的对角线AC,BD交于点O,EF过点0,分别交AD,BC于点E,F.下列结论:①OE=OF;②AE=BF;③∠DOC=∠OCD;④∠CFE=∠DEF,其中结论一定成立的个数是( )
A.1 B.2 C.3 D.4
16.如图,平行四边形ABCD的顶点A,B,C的坐标分别是(0,1),(-2,-2),(2,-2),则顶点D的坐标是____________.
17.如图,将平行四边形ABCD沿对角线AC翻折,点B落在点E处,CE交AD于点F,若∠B=80°,∠ACE=2∠ECD,FC=a,FD=b,则平行四边形ABCD的周长为____________.
18.已知:如图,四边形ABCD为平行四边形,点E、A、C、F在同一直线上,AE=CF.
求证:(1)△ADE≌△CBF;
(2)ED//BF.
19.问题:如图,在平行四边形ABCD中,AB=8,AD=5,∠DAB,∠ABC的平分线AE,BF分别与直线CD交于点E,F,求EF的长.
答案:EF=2.
探究:
(1)把“问题”中的条件“AB=8”去掉,其余条件不变.
①当点E与点F重合时,求AB的长;
②当点E与点C重合时,求EF的长.
(2)把“问题”中的条件“AB=8,AD=5”去掉,其余条件不变,当D,F,E,C相邻两点间的距离相等时,求 的值.
20.[直观想象、逻辑推理]如图①,在平行四边形ABCD中,对角线AC、BD相交于点O,过O点作直线EF,分别交BC、AD于点E、F.
(1)证明:OF=OE;
(2)小明从图①中找到了一种将平行四边形的面积平分的方法.图②是一块纸片,其形状是一个大的平行四边形在一角剪去一个小的平行四边形,小明发现可以用一条直线将纸片分割成面积相等的两部分,请你帮助小明设计三种不同的分割方案.
参考答案
基础过关
1.C ∵AC∥HD∥GE,AG∥BF∥CE,∴四边形AHOB、四边形HGFO、四边形BODC、四边形OFED、四边形AGFB、四边形BFEC、四边形AHDC、四边形HGED、四边形AGEC都是平行四边形,共9个,故选C.
2.A 因为四边形ABCD为平行四边形,∠A+∠C=110°,所以∠A=∠C=55°,AD∥BC,所以∠A+∠B=180°,所以∠B=180°-∠A=125°,故选A.
3.B ∵四边形ABCD为平行四边形,AD=8,∴BC=AD=8,AD∥BC,
∴CE=BC-BE=8-3=5,∠ADE=∠CED,
∵DE平分∠ADC,∴∠ADE=∠CDE,∴∠CDE=∠CED,∴CD=CE=5,故选B.
4.D ∵四边形ABCD为平行四边形,且周长为26cm,∴AB+BC=13cm,OA=OC,
∵△BOC的周长比△AOB的周长多3cm,∴(OB+OC+BC)-(OA+OB+AB)=BC-AB=3 cm,
∴AB=5cm,BC=8 cm.故选D.
5.A 因为AF⊥DE,所以∠AFD=90°,所以∠ADF=90°-∠DAF=40°,因为DE平分∠ADC,所以∠ADC=2∠ADF=80°,因为四边形ABCD是平行四边形,所以AD∥BC,所以∠C+∠ADC=180°,所以∠C=180°-∠ADC=100°.
6.D 在平行四边形ABCD中,AD=BC,CD=AB.
∵M为CD的中点,AB=2BC,
∴∠DAM=∠DMA,∠CBM=∠CMB,
∵∠C+∠D=180°,∠C+∠CMB+∠CBM=180°,∠D+∠DAM+∠DMA=180°,
∴∠C=2∠DMA,∠D=2∠CMB,
∴∠AMB=180°-(∠DMA+∠CMB)=90°,即△MAB为直角三角形,
故选D.
7.证明 ∵四边形ABCD是平行四边形,
∴AD=CB,AD∥BC,∴∠ADE=∠CBF,
在△ADE和△CBF中∴△ADE≌△CBF(SAS),
∴∠AED=∠CFB,∴AE∥CF.
8.解析 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∠BAD=∠BCD,∴∠ABE=∠CDF,
∵AE平分∠BAD,CF平分∠BCD,
∴∠BAE=∠DCF,∴△ABE≌△CDF(ASA),∴AE=CF.
(2)∵四边形ABCD是平行四边形,∴AD∥BC,∠BAD+∠ABC=180°,
∵∠ABC=70°,∴∠BAD=110°,
∵AM平分∠BAD,AD∥BC,∴∠DAM=∠BAM=55°,∠DAM=∠AMB,∴∠AMB=55°.
9.答案 39
解析 如图,分别过点D、E作直线AB的垂线,垂足为F、G,∴ DF∥EG.
∵四边形ABCD为平行四边形,∴AB∥DC,∴DF=EG,
10.答案 3
解析 由题意可知,△ADC与△BCD的面积相等,△ADB与△BCA的面积相等,△ADO与△BCO的面积相等,共有3对.
能力提升
11.C ∵四边形ABCD是平行四边形,∴AD∥BC,DC∥AB,
∴∠A+∠ABC=180°,∠ABE+∠DEB=180°,
∵∠A=60°,∴∠ABC=120°,
∵BE平分∠ABC,∴∠ABE=60°,
∴∠DEB=180°-60°=120°,故选C.
12.B ∵四边形ABCD为平行四边形,∴BC=AD=5.
∵AC⊥BC,∴△ACB是直角三角形.
故选B.
13.B ∵四边形ABCD是平行四边形,
∴AB=CD,∠B=∠D=56°,
∵BE=CD,∴ AB=BE,∴△ABE是等腰三角形,
故选B.
14.D ∵四边形ABCD为平行四边形,
∴BO=DO,AO=OC=2cm,BC=AD=5cm,∴AC=4cm,
∵AB⊥AC,∴∠BAO=90°,
在Rt△ABO中,由勾股定理得
故选D.
15.A ∵四边形ABCD为平行四边形,∴AO=CO,BO=DO,AD∥BC,∴∠EAO=∠FCO,
在△AOE和△COF中∴△AOE≌△COF(ASA),
∴OE=OF,AE=CF,∠CFE=∠AEF,∴①一定成立,②④不一定成立.③不一定成立,
故选A.
16.答案 (4,1)
解析 ∵点B,C的坐标分别是(-2,-2),(2,-2),∴BC=2-(-2)=2+2=4,
∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC=4,
∵点A的坐标为(0,1),∴点D的坐标为(4,1).
17.答案
解析 ∵四边形ABCD为平行四边形,∠B=80°,∴AD∥BC,∠D=80°.
由折叠可知∠ACB=∠ACE,又AD∥BC,∴∠DAC=∠ACB,∴∠ACE=∠DAC,
∴△AFC为等腰三角形.∴AF=FC=a.
设∠ECD=x,则∠ACE=2x,∴∠DAC=2x,
在△ADC中,由三角形内角和定理可知2x+2x+x+80°=180°,解得x=20°.
∴∠DFC=4x=80°,∴△DFC为等腰三角形.∴DC=FC=a.
∵AD=AF+FD=a+b,∴平行四边形ABCD的周长为2(DC+AD)=2(a+a+b)=4a+2b.
18.证明 (1)∵四边形ABCD为平行四边形,
∴DA=BC,DA∥BC,∴∠DAC=∠BCA,
∵∠DAC+∠EAD=180°,∠BCA+∠FCB=180°,∴∠EAD=∠FCB,
在△ADE和△CBF中∴△ADE≌△CBF(SAS).
(2)由(1)知△ADE≌△CBF,∴∠E=∠F,∴ED∥BF.
19.解析 (1)①如图所示:
∵四边形ABCD是平行四边形,∴CD=AB,BC=AD=5,AB∥CD,∴∠DEA=∠BAE,
∵AE平分∠DAB,∴∠DAE=∠BAE,∴∠DEA=∠DAE,∴DE=AD=5,同理CF=BC=5,
∵点E与点F重合,∴AB=CD=DE+CF=10.
②如图所示:
当点E与点C重合时,易得DE=AD=5,CF=BC=5,∴点F与点D重合,∴EF=AD=5.
(2)分三种情况:
①如图1所示:
易得AD=DE,
∵C,D,E,F相邻两点间的距离相等,
②如图2所示.
易得AD=DE=CF,DF=FE=CE,
③如图3所示:
易得AD=DE=CF,DF=DC=CE,
综上所述, 的值为 式 或2.
20.解析 (1)证明:∵四边形ABCD是平行四边形,∴AO=CO,AD∥BC,∴∠FAO=∠ECO.
在△AOF和△COE中∴△AOF≌△COE(ASA),∴OF=OE.
(2)如图所示:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
