5.2 平行四边形的判定 同步练习(含解析)
文档属性
| 名称 | 5.2 平行四边形的判定 同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 8.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 09:37:07 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第五章 平行四边形
2 平行四边形的判定
基础过关
知识点1 平行四边形的判定定理(一)
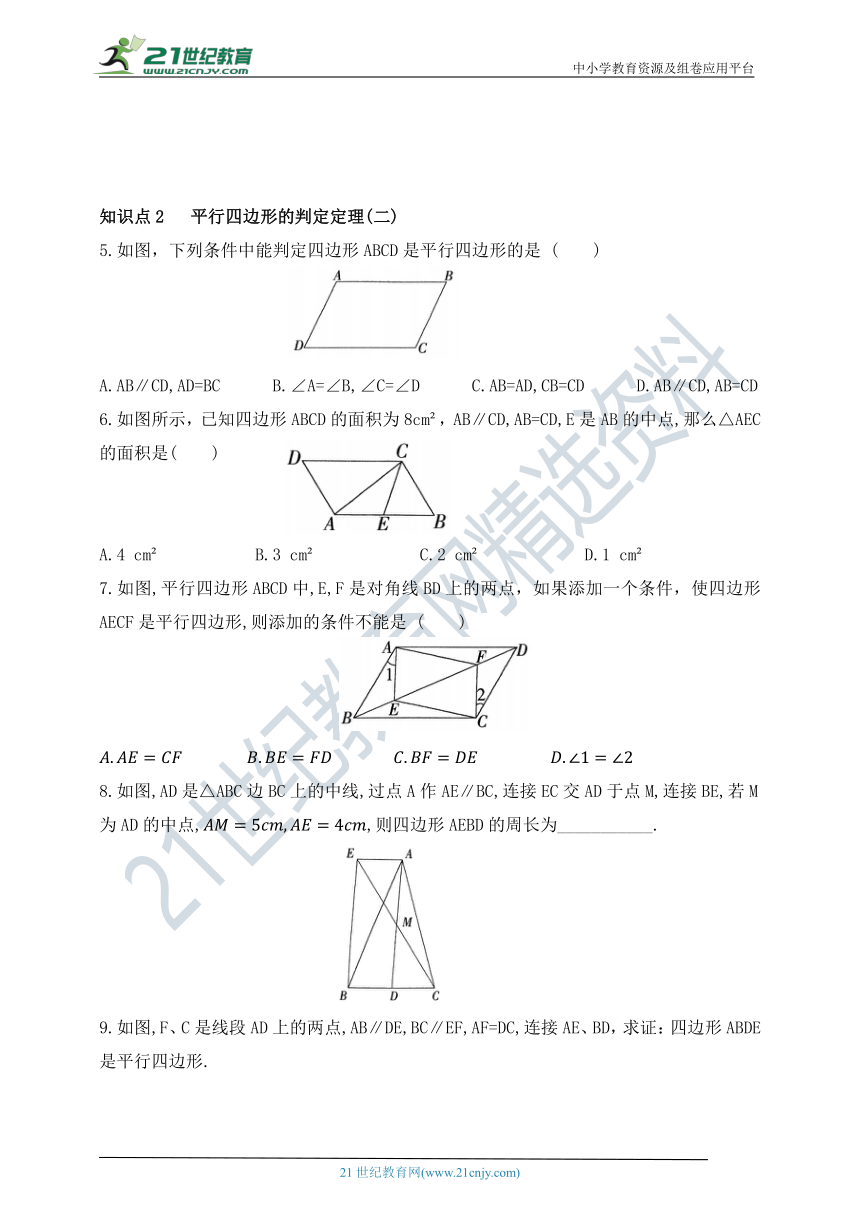
1.如图,点D是直线外一点,在直线上取两点A,B,连接AD,分别以点B,D为圆心,以AD,AB的长为半径画弧,两弧交于点C,连接CD,BC,则四边形ABCD是平行四边形,理由是_____________________________________________________.
2.如图,在四边形ABCD中,AB=CD=2,AD=BC=5,∠BCD的平分线交AD于点F,交BA的延长
线于点E,则AE的长为____________.
3.如图,已知CD∥AB,∠B=∠C,求证:AC∥BD.
4.如图,∠MON=∠PMO,OP=x-3,OM=4,ON=3,MN=5,MP=11-x.求证:四边形OPMN是平行四边形.
知识点2 平行四边形的判定定理(二)
5.如图,下列条件中能判定四边形ABCD是平行四边形的是 ( )
A.AB∥CD,AD=BC B.∠A=∠B,∠C=∠D C.AB=AD,CB=CD D.AB∥CD,AB=CD
6.如图所示,已知四边形ABCD的面积为8cm ,AB∥CD,AB=CD,E是AB的中点,那么△AEC的面积是( )
A.4 cm B.3 cm C.2 cm D.1 cm
7.如图,平行四边形ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使四边形AECF是平行四边形,则添加的条件不能是 ( )
8.如图,AD是△ABC边BC上的中线,过点A作AE∥BC,连接EC交AD于点M,连接BE,若M为AD的中点,,则四边形AEBD的周长为___________.
9.如图,F、C是线段AD上的两点,AB∥DE,BC∥EF,AF=DC,连接AE、BD,求证:四边形ABDE是平行四边形.
知识点3 平行四边形的判定定理(三)
10.如图,A,B,C,D在同一条直线上,且AB=CD,AE=DF,AE∥DF.求证:四边形EBFC是平行四边形.
11.如图,平行四边形ABCD的对角线相交于点O,直线EF过点O,分别交BC、AD于点E、F,点G、H分别为OB、OD的中点,求证:四边形GEHF是平行四边形.
能力提升
12.如图1,平行四边形ABCD中,,∠ABC为锐角,要在对角线BD上找点N,M,使四边形ANCM为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案是( )
图1 图2
A.甲、乙、丙 B.只有甲、乙 C.只有甲、丙 D.只有乙、丙
13.如图四边形ABCD的对角线AC和BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
A.OA=OC,AB∥DC B.∠ABC=∠ADC,AD∥BC
C.∠ABD=∠ADB,∠BAO=∠DCO D.AB=DC,AD=BC
14.如图BD垂直平分AC,交AC于E,∠BCD=∠ADF,FA⊥AC,垂足为A,AF=DF=5,AD=6,则AC的长为( )
A.9.5 B.9.6 C.9.7 D.9.8
15.如图,在四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为点E,F.
(1)请你只添加一个条件(不另加辅助线),使得四边形AECF为平行四边形,你添加的条件是________________;
(2)添加条件后,证明四边形AECF为平行四边形.
16.如图,点A,E,F,C在同一条直线上,AE=CF,过点E,F分别作DE⊥AC,BF⊥AC,AB∥CD.求证:AC与BD互相平分.
17.如图,在四边形ABCD中,AD∥BC,对角线AC、BD交于点O,且AO=OC,过点O作EF⊥BD,交AD于点E,交BC于点F.
(1)求证:四边形ABCD为平行四边形;
(2)连接BE,若∠BAD=100°,∠DBF=2∠ABE,求∠ABE的度数.
18.[逻辑推理]在四边形ABCD中,AD∥BC,BC⊥CD,AD=6cm,BC=10cm,M是BC上一点,且BM=4cm,点E从点A出发以1cm/s的速度向点D运动,点F从点B出发以2cm/s的速度向点C运动,E、F两点同时开始运动,当其中一点到达终点时,另一点也随之停止.设运动时间为ts,当t的值为_________时,以A、M、E、F为顶点的四边形是平行四边形.
19.[逻辑推理]如图,已知平行四边形ABCO的顶点A、C分别在直线x=2和x=7上,O是坐标原点,求对角线OB长的最小值.
参考答案
基础过关
1.答案 两组对边分别相等的四边形是平行四边形
解析 根据尺规作图的画法可得AB=DC,AD=BC,∴四边形ABCD是平行四边形.
2.答案 3
解析 ∵AB=CD,AD=BC,∴四边形ABCD是平行四边形,∴AB∥CD,∴∠E=∠DCE,
∵CE平分∠BCD,∴∠DCE=∠BCE,∴∠E=∠BCE,∴BE=BC=5,
∵AB=2,∴AE=5-2=3.
3.证明 证法一:如图:
∵CD∥AB,∴∠1=∠2.
在△ACD和△DBA中∴△ACD≌△DBA(AAS),
∴AC=BD,AB=CD,∴四边形ABDC为平行四边形,∴AC∥BD.
证法二:∵CD//AB,∴∠C+∠CAB=180°.
又∵∠B=∠C,∴∠B+∠CAB=180°,∴AC∥BD.
4.证明 在△MON中,OM=4,ON=3,MN=5,
因此
∴△MON是直角三角形.∴∠MON=∠PMO=90°.
在Rt△POM中,OP=x-3,OM=4,MP=11-x,
由勾股定理可得 即 解得x=8,
∴OP=8-3=5,MP=11-8=3,∴OP=MN,MP=ON,
∴四边形OPMN是平行四边形.
5.D A项,由AB∥CD,AD=BC可知,四边形ABCD可能是梯形,故A错误;B项,由∠A=∠B,∠C=∠D可知,四边形ABCD可能是等腰梯形,故B错误;C项,由AB=AD,CB=CD可知,四边形ABCD可能是筝形;D项,由AB∥CD,AB=CD可知,四边形ABCD为平行四边形.故选D.
6.C ∵AB∥CD,AB=CD,∴四边形ABCD是平行四边形,
E是AB的中点,
故选C.
7.A 当添加的条件为BE=FD时,
∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠ABD=∠CDB.
又∵BE=DF,∴△ABE≌△CDF(SAS),∴AE=CF,∠AEB=∠CFD,
∴∠AEF=∠CFE,∴AE∥CF,∴四边形AECF是平行四边形,故B不合题意;
当添加的条件为BF=DE时,
∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠ABD=∠CDB,
又∵BF=DE,∴BF-EF=DE-EF,∴BE=DF,∴△ABE≌△CDF(SAS),
∴AE=CF,∠AEB=∠CFD,∴∠AEF=∠CFE,∴AE∥CF,
∴四边形AECF是平行四边形,故C不合题意;
当添加的条件为∠1=∠2时,
∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠ABD=∠CDB,
又∵∠1=∠2,∴△ABE≌△CDF(ASA),∴AE=CF,∠AEB=∠CFD,∴∠AEF=∠CFE,∴AE∥CF,
∴四边形AECF是平行四边形,故D不合题意;
添加AE=CF后,不能得出△ABE≌△CDF,进而得不出四边形AECF是平行四边形,故选A.
8.答案 28 cm
解析 ∵AD是△ABC的中线,∴BD=CD,
∵点M为AD的中点,∴AM=DM,∵AE∥BC,∴∠EAM=∠CDA,
在△EAM和△CDM中∴△EAM≌△CDM(ASA),∴AE=CD,
又∵BD=CD,∴AE=BD,∵AE∥BC,∴四边形AEBD为平行四边形,
∴四边形AEBD的周长=2(AD+AE)=2(2AM+AE)=2×(10+4)=28 cm.
9.证明 ∵AF=DC,∴AF+FC=DC+FC,∴AC=DF,
∵AB∥DE,∴∠BAC=∠EDF,∵BC∥EF,∴∠ACB=∠EFD.
在△ABC和△DEF中∴△ABC≌△DEF(ASA),∴AB=DE,
又∵AB∥DE,∴四边形ABDE是平行四边形.
10.证明 如图,连接AF,ED,EF,设EF交AD于点O.
∵AE=DF,AE∥DF,∴四边形AEDF为平行四边形,∴EO=FO,AO=DO,
又∵AB=CD,∴AO-AB=DO-CD,∴BO=CO,
又∵EO=FO,∴四边形EBFC是平行四边形.
11.证明 ∵四边形ABCD为平行四边形,∴BO=DO,AD=BC,AD∥BC.∴∠ADO=∠CBO.
在△FOD和△EOB中∴△FOD≌△EOB(ASA).∴FO=EO.
又∵G、H分别为OB、OD的中点,∴GO=HO.∴四边形GEHF是平行四边形.
能力提升
12.A 方案甲中:连接AC,如图所示:
∵四边形ABCD是平行四边形,O为BD的中点,∴OB=OD,OA=OC,
∵BN=NO,OM=MD,∴NO=OM,∴四边形ANCM为平行四边形,方案甲正确;
方案乙中:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠ABN=∠CDM,
∵AN⊥BD,CM⊥BD,∴AN∥CM,∠ANB=∠CMD,
在△ABN和△CDM中∴△ABN≌△CDM(AAS),∴AN=CM,
又∵AN∥CM,∴四边形ANCM为平行四边形,方案乙正确;
方案丙中:∵四边形ABCD是平行四边形,∴∠BAD=∠BCD,AB=CD,AB∥CD,∴∠ABN=∠CDM,
∵AN平分∠BAD,CM平分∠BCD,∴∠BAN=∠DCM,
在△ABN和△CDM中∴△ABN≌△CDM(ASA),∴AN=CM,∠ANB=∠CMD,
∴∠ANM=∠CMN,∴AN∥CM,∴四边形ANCM为平行四边形,方案丙正确.故选A.
13.C A项,∵AB∥CD,∴∠BAC=∠ACD,
在△ABO和△CDO中∴△ABO≌△CDO(ASA),∴OB=OD,
又∵OA=OC,∴四边形ABCD为平行四边形,故选项A不合题意;
B项,∵AD∥BC,∴∠ADC+∠BCD=180°,
又∵∠ABC=∠ADC,∴∠ABC+∠BCD=180°,∴AB∥CD,
又∵AD∥BC,∴四边形ABCD为平行四边形,故选项B不合题意;
D项,∵AB=DC,AD=BC,∴四边形ABCD为平行四边形,故选项D不合题意.故选C.
14.B ∵BD垂直平分AC,∴DA=DC,BA=BC,∴∠DAC=∠DCA,∠BAC=∠BCA,∴ ∠DAC+∠BAC=∠DCA+∠BCA,即∠DAB=∠BCD,
∵∠BCD=∠ADF,∴∠DAB=∠ADF,∴AB∥DF,∵FA⊥AC,D B⊥AC,∴AF∥BD,∴四边形AFDB为平行四边形,∴BD=AF=5,AB=DF=5,设BE=x,则DE=5-x,
在Rt△AEB中, 在Rt△AED中,
即 解得x故选B.
15.解析 (1)答案不唯一,如:AE=CF.
(2)答案不唯一,需要与(1)中添加的条件相对应.
证明:∵AE⊥BD,CF⊥BD,∴AE∥CF,
∵AE=CF,∴四边形AECF为平行四边形.
16.证明 连接AD、BC,如图所示:
∵AB∥CD,∴∠BAF=∠DCE,
∵AE=CF,∴AE+EF=CF+EF,即AF=CE,
∵DE⊥AC,BF⊥AC,∴∠AFB=∠CED=90°,
在△ABF和△CDE中∴△ABF≌△CDE(ASA),∴AB=CD,
又∵AB∥CD,∴四边形ABCD是平行四边形,∴AC与BD互相平分.
17.解析 (1)证明:∵AD∥BC,∴∠OAD=∠OCB.
在△AOD和△COB中,∴△AOD≌△COB(ASA),∴AD=CB,
又∵AD∥BC,∴四边形ABCD为平行四边形.
(2)设∠ABE=x,则∠DBF=2x,
由(1)得四边形ABCD为平行四边形,∴OB=OD,
又∵EF⊥BD,∴BE=DE,∴∠EBD=∠EDB,
∵AD∥BC,∴∠EDB=∠DBF,∴∠EBD=∠EDB=∠DBF=2x.
在△ABD中,∠BAD+∠ABE+∠EBD+∠EDB=180°,∴100°+x+2x+2x=180°,解得x=16°,即∠ABE=16°.
18.答案 4或
解析 由题意知AE=t cm,BF=2t cm.①当点F在线段BM上(0≤t<2),AE=FM时,以A、M、E、F为顶点的四边形是平行四边形,此时FM=(4-2t) cm,令t=4-2t,解得
②当点F在线段CM上(2此时FM=(2t-4) cm,令t=2t-4,解得t=4.
综上所述,当t=4或 时,以A、M、E、F为顶点的四边形是平行四边形.
19.解析 过点B作BD⊥直线x=7于点D,过点B作BE⊥x轴于点E,设直线x=2与OC交于点M,与x轴交于点F,直线x=7与AB交于点N,如图.
∵四边形OABC是平行四边形,∴∠OAB=∠BCO,OC∥AB,OA=BC,
∵直线x=2与直线x=7均垂直于x轴,∴AM∥CN,
又∵CM∥AN,∴四边形ANCM是平行四边形,
∴∠MAN=∠NCM,∴∠OAB-∠MAN=∠BCO-∠NCM,∴∠OAF=∠BCD,
∵∠OFA=∠BDC=90°,∴∠FOA=∠DBC.
在△OAF和△BCD中∴△OAF≌△BCD(ASA).∴BD=OF=2,∴OE=7+2=9.
在Rt△OEB中,由勾股定理得 且OE的长不变,
∴当BE的长最小,即B点在x轴上时,OB的长取得最小值,此时最小值为9.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 平行四边形
2 平行四边形的判定
基础过关
知识点1 平行四边形的判定定理(一)
1.如图,点D是直线外一点,在直线上取两点A,B,连接AD,分别以点B,D为圆心,以AD,AB的长为半径画弧,两弧交于点C,连接CD,BC,则四边形ABCD是平行四边形,理由是_____________________________________________________.
2.如图,在四边形ABCD中,AB=CD=2,AD=BC=5,∠BCD的平分线交AD于点F,交BA的延长
线于点E,则AE的长为____________.
3.如图,已知CD∥AB,∠B=∠C,求证:AC∥BD.
4.如图,∠MON=∠PMO,OP=x-3,OM=4,ON=3,MN=5,MP=11-x.求证:四边形OPMN是平行四边形.
知识点2 平行四边形的判定定理(二)
5.如图,下列条件中能判定四边形ABCD是平行四边形的是 ( )
A.AB∥CD,AD=BC B.∠A=∠B,∠C=∠D C.AB=AD,CB=CD D.AB∥CD,AB=CD
6.如图所示,已知四边形ABCD的面积为8cm ,AB∥CD,AB=CD,E是AB的中点,那么△AEC的面积是( )
A.4 cm B.3 cm C.2 cm D.1 cm
7.如图,平行四边形ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使四边形AECF是平行四边形,则添加的条件不能是 ( )
8.如图,AD是△ABC边BC上的中线,过点A作AE∥BC,连接EC交AD于点M,连接BE,若M为AD的中点,,则四边形AEBD的周长为___________.
9.如图,F、C是线段AD上的两点,AB∥DE,BC∥EF,AF=DC,连接AE、BD,求证:四边形ABDE是平行四边形.
知识点3 平行四边形的判定定理(三)
10.如图,A,B,C,D在同一条直线上,且AB=CD,AE=DF,AE∥DF.求证:四边形EBFC是平行四边形.
11.如图,平行四边形ABCD的对角线相交于点O,直线EF过点O,分别交BC、AD于点E、F,点G、H分别为OB、OD的中点,求证:四边形GEHF是平行四边形.
能力提升
12.如图1,平行四边形ABCD中,,∠ABC为锐角,要在对角线BD上找点N,M,使四边形ANCM为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案是( )
图1 图2
A.甲、乙、丙 B.只有甲、乙 C.只有甲、丙 D.只有乙、丙
13.如图四边形ABCD的对角线AC和BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
A.OA=OC,AB∥DC B.∠ABC=∠ADC,AD∥BC
C.∠ABD=∠ADB,∠BAO=∠DCO D.AB=DC,AD=BC
14.如图BD垂直平分AC,交AC于E,∠BCD=∠ADF,FA⊥AC,垂足为A,AF=DF=5,AD=6,则AC的长为( )
A.9.5 B.9.6 C.9.7 D.9.8
15.如图,在四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为点E,F.
(1)请你只添加一个条件(不另加辅助线),使得四边形AECF为平行四边形,你添加的条件是________________;
(2)添加条件后,证明四边形AECF为平行四边形.
16.如图,点A,E,F,C在同一条直线上,AE=CF,过点E,F分别作DE⊥AC,BF⊥AC,AB∥CD.求证:AC与BD互相平分.
17.如图,在四边形ABCD中,AD∥BC,对角线AC、BD交于点O,且AO=OC,过点O作EF⊥BD,交AD于点E,交BC于点F.
(1)求证:四边形ABCD为平行四边形;
(2)连接BE,若∠BAD=100°,∠DBF=2∠ABE,求∠ABE的度数.
18.[逻辑推理]在四边形ABCD中,AD∥BC,BC⊥CD,AD=6cm,BC=10cm,M是BC上一点,且BM=4cm,点E从点A出发以1cm/s的速度向点D运动,点F从点B出发以2cm/s的速度向点C运动,E、F两点同时开始运动,当其中一点到达终点时,另一点也随之停止.设运动时间为ts,当t的值为_________时,以A、M、E、F为顶点的四边形是平行四边形.
19.[逻辑推理]如图,已知平行四边形ABCO的顶点A、C分别在直线x=2和x=7上,O是坐标原点,求对角线OB长的最小值.
参考答案
基础过关
1.答案 两组对边分别相等的四边形是平行四边形
解析 根据尺规作图的画法可得AB=DC,AD=BC,∴四边形ABCD是平行四边形.
2.答案 3
解析 ∵AB=CD,AD=BC,∴四边形ABCD是平行四边形,∴AB∥CD,∴∠E=∠DCE,
∵CE平分∠BCD,∴∠DCE=∠BCE,∴∠E=∠BCE,∴BE=BC=5,
∵AB=2,∴AE=5-2=3.
3.证明 证法一:如图:
∵CD∥AB,∴∠1=∠2.
在△ACD和△DBA中∴△ACD≌△DBA(AAS),
∴AC=BD,AB=CD,∴四边形ABDC为平行四边形,∴AC∥BD.
证法二:∵CD//AB,∴∠C+∠CAB=180°.
又∵∠B=∠C,∴∠B+∠CAB=180°,∴AC∥BD.
4.证明 在△MON中,OM=4,ON=3,MN=5,
因此
∴△MON是直角三角形.∴∠MON=∠PMO=90°.
在Rt△POM中,OP=x-3,OM=4,MP=11-x,
由勾股定理可得 即 解得x=8,
∴OP=8-3=5,MP=11-8=3,∴OP=MN,MP=ON,
∴四边形OPMN是平行四边形.
5.D A项,由AB∥CD,AD=BC可知,四边形ABCD可能是梯形,故A错误;B项,由∠A=∠B,∠C=∠D可知,四边形ABCD可能是等腰梯形,故B错误;C项,由AB=AD,CB=CD可知,四边形ABCD可能是筝形;D项,由AB∥CD,AB=CD可知,四边形ABCD为平行四边形.故选D.
6.C ∵AB∥CD,AB=CD,∴四边形ABCD是平行四边形,
E是AB的中点,
故选C.
7.A 当添加的条件为BE=FD时,
∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠ABD=∠CDB.
又∵BE=DF,∴△ABE≌△CDF(SAS),∴AE=CF,∠AEB=∠CFD,
∴∠AEF=∠CFE,∴AE∥CF,∴四边形AECF是平行四边形,故B不合题意;
当添加的条件为BF=DE时,
∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠ABD=∠CDB,
又∵BF=DE,∴BF-EF=DE-EF,∴BE=DF,∴△ABE≌△CDF(SAS),
∴AE=CF,∠AEB=∠CFD,∴∠AEF=∠CFE,∴AE∥CF,
∴四边形AECF是平行四边形,故C不合题意;
当添加的条件为∠1=∠2时,
∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠ABD=∠CDB,
又∵∠1=∠2,∴△ABE≌△CDF(ASA),∴AE=CF,∠AEB=∠CFD,∴∠AEF=∠CFE,∴AE∥CF,
∴四边形AECF是平行四边形,故D不合题意;
添加AE=CF后,不能得出△ABE≌△CDF,进而得不出四边形AECF是平行四边形,故选A.
8.答案 28 cm
解析 ∵AD是△ABC的中线,∴BD=CD,
∵点M为AD的中点,∴AM=DM,∵AE∥BC,∴∠EAM=∠CDA,
在△EAM和△CDM中∴△EAM≌△CDM(ASA),∴AE=CD,
又∵BD=CD,∴AE=BD,∵AE∥BC,∴四边形AEBD为平行四边形,
∴四边形AEBD的周长=2(AD+AE)=2(2AM+AE)=2×(10+4)=28 cm.
9.证明 ∵AF=DC,∴AF+FC=DC+FC,∴AC=DF,
∵AB∥DE,∴∠BAC=∠EDF,∵BC∥EF,∴∠ACB=∠EFD.
在△ABC和△DEF中∴△ABC≌△DEF(ASA),∴AB=DE,
又∵AB∥DE,∴四边形ABDE是平行四边形.
10.证明 如图,连接AF,ED,EF,设EF交AD于点O.
∵AE=DF,AE∥DF,∴四边形AEDF为平行四边形,∴EO=FO,AO=DO,
又∵AB=CD,∴AO-AB=DO-CD,∴BO=CO,
又∵EO=FO,∴四边形EBFC是平行四边形.
11.证明 ∵四边形ABCD为平行四边形,∴BO=DO,AD=BC,AD∥BC.∴∠ADO=∠CBO.
在△FOD和△EOB中∴△FOD≌△EOB(ASA).∴FO=EO.
又∵G、H分别为OB、OD的中点,∴GO=HO.∴四边形GEHF是平行四边形.
能力提升
12.A 方案甲中:连接AC,如图所示:
∵四边形ABCD是平行四边形,O为BD的中点,∴OB=OD,OA=OC,
∵BN=NO,OM=MD,∴NO=OM,∴四边形ANCM为平行四边形,方案甲正确;
方案乙中:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠ABN=∠CDM,
∵AN⊥BD,CM⊥BD,∴AN∥CM,∠ANB=∠CMD,
在△ABN和△CDM中∴△ABN≌△CDM(AAS),∴AN=CM,
又∵AN∥CM,∴四边形ANCM为平行四边形,方案乙正确;
方案丙中:∵四边形ABCD是平行四边形,∴∠BAD=∠BCD,AB=CD,AB∥CD,∴∠ABN=∠CDM,
∵AN平分∠BAD,CM平分∠BCD,∴∠BAN=∠DCM,
在△ABN和△CDM中∴△ABN≌△CDM(ASA),∴AN=CM,∠ANB=∠CMD,
∴∠ANM=∠CMN,∴AN∥CM,∴四边形ANCM为平行四边形,方案丙正确.故选A.
13.C A项,∵AB∥CD,∴∠BAC=∠ACD,
在△ABO和△CDO中∴△ABO≌△CDO(ASA),∴OB=OD,
又∵OA=OC,∴四边形ABCD为平行四边形,故选项A不合题意;
B项,∵AD∥BC,∴∠ADC+∠BCD=180°,
又∵∠ABC=∠ADC,∴∠ABC+∠BCD=180°,∴AB∥CD,
又∵AD∥BC,∴四边形ABCD为平行四边形,故选项B不合题意;
D项,∵AB=DC,AD=BC,∴四边形ABCD为平行四边形,故选项D不合题意.故选C.
14.B ∵BD垂直平分AC,∴DA=DC,BA=BC,∴∠DAC=∠DCA,∠BAC=∠BCA,∴ ∠DAC+∠BAC=∠DCA+∠BCA,即∠DAB=∠BCD,
∵∠BCD=∠ADF,∴∠DAB=∠ADF,∴AB∥DF,∵FA⊥AC,D B⊥AC,∴AF∥BD,∴四边形AFDB为平行四边形,∴BD=AF=5,AB=DF=5,设BE=x,则DE=5-x,
在Rt△AEB中, 在Rt△AED中,
即 解得x故选B.
15.解析 (1)答案不唯一,如:AE=CF.
(2)答案不唯一,需要与(1)中添加的条件相对应.
证明:∵AE⊥BD,CF⊥BD,∴AE∥CF,
∵AE=CF,∴四边形AECF为平行四边形.
16.证明 连接AD、BC,如图所示:
∵AB∥CD,∴∠BAF=∠DCE,
∵AE=CF,∴AE+EF=CF+EF,即AF=CE,
∵DE⊥AC,BF⊥AC,∴∠AFB=∠CED=90°,
在△ABF和△CDE中∴△ABF≌△CDE(ASA),∴AB=CD,
又∵AB∥CD,∴四边形ABCD是平行四边形,∴AC与BD互相平分.
17.解析 (1)证明:∵AD∥BC,∴∠OAD=∠OCB.
在△AOD和△COB中,∴△AOD≌△COB(ASA),∴AD=CB,
又∵AD∥BC,∴四边形ABCD为平行四边形.
(2)设∠ABE=x,则∠DBF=2x,
由(1)得四边形ABCD为平行四边形,∴OB=OD,
又∵EF⊥BD,∴BE=DE,∴∠EBD=∠EDB,
∵AD∥BC,∴∠EDB=∠DBF,∴∠EBD=∠EDB=∠DBF=2x.
在△ABD中,∠BAD+∠ABE+∠EBD+∠EDB=180°,∴100°+x+2x+2x=180°,解得x=16°,即∠ABE=16°.
18.答案 4或
解析 由题意知AE=t cm,BF=2t cm.①当点F在线段BM上(0≤t<2),AE=FM时,以A、M、E、F为顶点的四边形是平行四边形,此时FM=(4-2t) cm,令t=4-2t,解得
②当点F在线段CM上(2
综上所述,当t=4或 时,以A、M、E、F为顶点的四边形是平行四边形.
19.解析 过点B作BD⊥直线x=7于点D,过点B作BE⊥x轴于点E,设直线x=2与OC交于点M,与x轴交于点F,直线x=7与AB交于点N,如图.
∵四边形OABC是平行四边形,∴∠OAB=∠BCO,OC∥AB,OA=BC,
∵直线x=2与直线x=7均垂直于x轴,∴AM∥CN,
又∵CM∥AN,∴四边形ANCM是平行四边形,
∴∠MAN=∠NCM,∴∠OAB-∠MAN=∠BCO-∠NCM,∴∠OAF=∠BCD,
∵∠OFA=∠BDC=90°,∴∠FOA=∠DBC.
在△OAF和△BCD中∴△OAF≌△BCD(ASA).∴BD=OF=2,∴OE=7+2=9.
在Rt△OEB中,由勾股定理得 且OE的长不变,
∴当BE的长最小,即B点在x轴上时,OB的长取得最小值,此时最小值为9.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
