5.3 三角形的中位线 同步练习(含解析)
文档属性
| 名称 | 5.3 三角形的中位线 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第五章 平行四边形
3 三角形的中位线
基础过关
知识点 三角形中位线的概念和性质
1.如图,A、B是被一个湖隔开的两个村庄,为了测量A、B两个村庄之间的距离,在直线AB外选一点C,连接AC、BC,再分别取线段AC、BC的中点E、F,测得EF=15m,则AB的长为( )
A.7.5 m B.15 m C.30 m D.45 m
2.如图,D、E、F分别是△ABC各边的中点,连接DE、EF、FD,则图中共有_______个平行四边形.( )
A.1 B.2 C.3 D.4
3.如图,DE是△ABC的中位线,∠ABC的平分线交DE于点F,AB=8,BC=12,则EF的长为( )
A.1 B.1.5 C.2 D.2.5
4.如图,在四边形ABCD中,AD=BC,∠DAB=50°,∠CBA=70°,P、M、N分别是AB、AC、BD的中点,若BC=6,则△PMN的周长是_________.
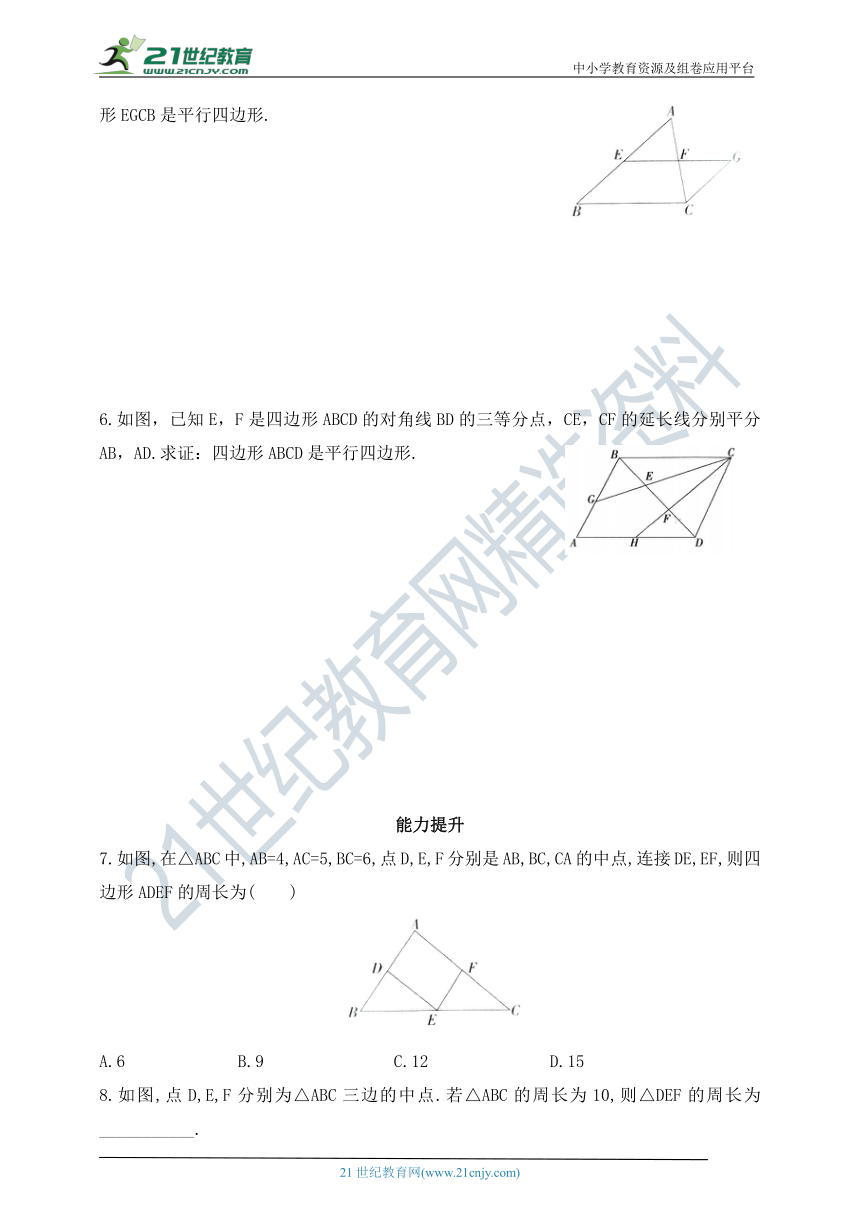
5.如图,在△ABC中,点E,F分别为边AB,AC的中点,延长EF到点G,使FG=EF.求证:四边形EGCB是平行四边形.
6.如图,已知E,F是四边形ABCD的对角线BD的三等分点,CE,CF的延长线分别平分AB,AD.求证:四边形ABCD是平行四边形.
能力提升
7.如图,在△ABC中,AB=4,AC=5,BC=6,点D,E,F分别是AB,BC,CA的中点,连接DE,EF,则四边形ADEF的周长为( )
A.6 B.9 C.12 D.15
8.如图,点D,E,F分别为△ABC三边的中点.若△ABC的周长为10,则△DEF的周长为___________.
9.如图,在Rt△ABC中,∠C=30°,D、E分别为AC、BC的中点,DE=2,过点B作BF∥AC,交DE的延长线于点F,则四边形ABFD的面积为 ___________.
10.如图,在△ABC中,AD是BC边上的中线,F是线段AC上一点,且满足2AF=CF,连接BF与AD相交于点E.若G为线段BF上一动点,当点G在什么位置时,四边形AFDG为平行四边形 请说明理由.
11.[数学抽象]如图,△ABC的周长为a,以△ABC的各边的中点为顶点作 再以 各边的中点为顶点作 ……如此作下去,则 的周长为( )
12.[逻辑推理]如图1,在四边形ABCD中,AB=CD,E,F分别是BC,AD的中点,连接EF并延
长,分别与BA,CD的延长线交于点M,N,则∠BME=∠CNE(不需证明).
小明的思路:在图1中,连接BD,取BD的中点H,连接HE,HF,根据三角形中位线定理和平行线的性质,可证得∠BME=∠CNE.
问题:如图2,在△ABC中,AC>AB,D点在AC上,AB=CD,E,F分别是BC,AD的中点,连接EF并延长,与BA的延长线交于点G,若∠EFC=60°,连接GD,判断△AGD的形状并证明.
参考答案
基础过关
1.C ∵E、F分别是AC、BC的中点,∴EF是△ABC的中位线,
∵EF=15m,∴AB=30m.故选C.
2.C ∵D、E、F分别是△ABC各边的中点,
∥∥∥
∴四边形ADFE、四边形BDEF和四边形CFDE为平行四边形,故选C.
3.C ∵DE是△ABC的中位线,∥∴∠DFB=∠FBC.
又∵BF平分∠ABC,∴∠DBF=∠FBC,∴∠DFB=∠DBF,∴DF=BD=4.∴EF=DE-DF=6-4=2,故选C.
4.答案 9
解析 ∵P、M分别是AB、AC的中点,∥∴∠APM=∠CBA=70°,
同理可得 ∥∴∠BPN=∠DAB=50°,PM=PN=3,
∴∠MPN=180°-50°-70°=60°,∴△PMN为等边三角形,∴MN=PM=3,
∴△PMN的周长为9.
5.证明 ∵E,F分别为AB,AC的中点,∴EF是△ABC的中位线, ∥
∵EF=FG,∴EG=BC.又∵EG∥BC,∴四边形EGCB是平行四边形.
6.证明 连接AC交BD于O,连接AE,AF,如图所示:
∵G是AB的中点,BE=EF,∴GE是△ABF的一条中位线,∴EG∥AF,即CE∥AF,
同理CF∥AE,∴四边形AFCE是平行四边形.∴OA=OC,OE=OF,
又∵BE=DF,∴OB=OD,∴四边形ABCD是平行四边形.
能力提升
7.B ∵点D,E,F分别是AB,BC,CA的中点,
∴四边形ADEF的周长9,故选B.
8.答案 5
解析 ∵D,E,F分别是AB,AC,BC的中点,∴FD,FE,DE为△ABC的中位线,
9.答案
解析 ∵D、E分别为AC、BC的中点,∴DE是△ABC的中位线,
∥∴AB=2DE,DF∥AB,
又∵BF∥AC,∴BF∥AD,∴四边形ABFD是平行四边形,
∵DE=2,∴AB=2×2=4.在Rt△ABC中,∵∠C=30°,∴AC=2AB=2×4=8,
∴
10.解析 当点G为线段BF的中点时,四边形AFDG为平行四边形.
理由:∵AD是BC边上的中线,∴BD=CD,
∵点G为线段BF的中点,∴DG是△BCF的中位线,
∴DG∥CF,2DG=CF,∴DG∥AF,
∵2AF=CF,∴ DG=AF,∴四边形AFDG为平行四边形.
分别为BC、AC、AB的中点,
的周长
同理, 的周长 则 的周长 故选A.
12.解析 △AGD是直角三角形.
证明:如图,连接BD,取BD的中点H,连接HF,HE,
∵F是AD的中点,∴HF是△ABD的中位线,∥∴∠1=∠3,
同理, ∥
∵AB=CD,∴HF=HE,∴∠1=∠2,∴∠3=∠2=∠EFC,
∵∠EFC=60°,∴∠3=∠EFC=∠AFG=60°,∴△AGF为等边三角形,
∵AF=FD,∴GF=FD,∴∠FGD=∠FDG=30°,∴∠AGD=30°+60°=90°,
∴△AGD是直角三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 平行四边形
3 三角形的中位线
基础过关
知识点 三角形中位线的概念和性质
1.如图,A、B是被一个湖隔开的两个村庄,为了测量A、B两个村庄之间的距离,在直线AB外选一点C,连接AC、BC,再分别取线段AC、BC的中点E、F,测得EF=15m,则AB的长为( )
A.7.5 m B.15 m C.30 m D.45 m
2.如图,D、E、F分别是△ABC各边的中点,连接DE、EF、FD,则图中共有_______个平行四边形.( )
A.1 B.2 C.3 D.4
3.如图,DE是△ABC的中位线,∠ABC的平分线交DE于点F,AB=8,BC=12,则EF的长为( )
A.1 B.1.5 C.2 D.2.5
4.如图,在四边形ABCD中,AD=BC,∠DAB=50°,∠CBA=70°,P、M、N分别是AB、AC、BD的中点,若BC=6,则△PMN的周长是_________.
5.如图,在△ABC中,点E,F分别为边AB,AC的中点,延长EF到点G,使FG=EF.求证:四边形EGCB是平行四边形.
6.如图,已知E,F是四边形ABCD的对角线BD的三等分点,CE,CF的延长线分别平分AB,AD.求证:四边形ABCD是平行四边形.
能力提升
7.如图,在△ABC中,AB=4,AC=5,BC=6,点D,E,F分别是AB,BC,CA的中点,连接DE,EF,则四边形ADEF的周长为( )
A.6 B.9 C.12 D.15
8.如图,点D,E,F分别为△ABC三边的中点.若△ABC的周长为10,则△DEF的周长为___________.
9.如图,在Rt△ABC中,∠C=30°,D、E分别为AC、BC的中点,DE=2,过点B作BF∥AC,交DE的延长线于点F,则四边形ABFD的面积为 ___________.
10.如图,在△ABC中,AD是BC边上的中线,F是线段AC上一点,且满足2AF=CF,连接BF与AD相交于点E.若G为线段BF上一动点,当点G在什么位置时,四边形AFDG为平行四边形 请说明理由.
11.[数学抽象]如图,△ABC的周长为a,以△ABC的各边的中点为顶点作 再以 各边的中点为顶点作 ……如此作下去,则 的周长为( )
12.[逻辑推理]如图1,在四边形ABCD中,AB=CD,E,F分别是BC,AD的中点,连接EF并延
长,分别与BA,CD的延长线交于点M,N,则∠BME=∠CNE(不需证明).
小明的思路:在图1中,连接BD,取BD的中点H,连接HE,HF,根据三角形中位线定理和平行线的性质,可证得∠BME=∠CNE.
问题:如图2,在△ABC中,AC>AB,D点在AC上,AB=CD,E,F分别是BC,AD的中点,连接EF并延长,与BA的延长线交于点G,若∠EFC=60°,连接GD,判断△AGD的形状并证明.
参考答案
基础过关
1.C ∵E、F分别是AC、BC的中点,∴EF是△ABC的中位线,
∵EF=15m,∴AB=30m.故选C.
2.C ∵D、E、F分别是△ABC各边的中点,
∥∥∥
∴四边形ADFE、四边形BDEF和四边形CFDE为平行四边形,故选C.
3.C ∵DE是△ABC的中位线,∥∴∠DFB=∠FBC.
又∵BF平分∠ABC,∴∠DBF=∠FBC,∴∠DFB=∠DBF,∴DF=BD=4.∴EF=DE-DF=6-4=2,故选C.
4.答案 9
解析 ∵P、M分别是AB、AC的中点,∥∴∠APM=∠CBA=70°,
同理可得 ∥∴∠BPN=∠DAB=50°,PM=PN=3,
∴∠MPN=180°-50°-70°=60°,∴△PMN为等边三角形,∴MN=PM=3,
∴△PMN的周长为9.
5.证明 ∵E,F分别为AB,AC的中点,∴EF是△ABC的中位线, ∥
∵EF=FG,∴EG=BC.又∵EG∥BC,∴四边形EGCB是平行四边形.
6.证明 连接AC交BD于O,连接AE,AF,如图所示:
∵G是AB的中点,BE=EF,∴GE是△ABF的一条中位线,∴EG∥AF,即CE∥AF,
同理CF∥AE,∴四边形AFCE是平行四边形.∴OA=OC,OE=OF,
又∵BE=DF,∴OB=OD,∴四边形ABCD是平行四边形.
能力提升
7.B ∵点D,E,F分别是AB,BC,CA的中点,
∴四边形ADEF的周长9,故选B.
8.答案 5
解析 ∵D,E,F分别是AB,AC,BC的中点,∴FD,FE,DE为△ABC的中位线,
9.答案
解析 ∵D、E分别为AC、BC的中点,∴DE是△ABC的中位线,
∥∴AB=2DE,DF∥AB,
又∵BF∥AC,∴BF∥AD,∴四边形ABFD是平行四边形,
∵DE=2,∴AB=2×2=4.在Rt△ABC中,∵∠C=30°,∴AC=2AB=2×4=8,
∴
10.解析 当点G为线段BF的中点时,四边形AFDG为平行四边形.
理由:∵AD是BC边上的中线,∴BD=CD,
∵点G为线段BF的中点,∴DG是△BCF的中位线,
∴DG∥CF,2DG=CF,∴DG∥AF,
∵2AF=CF,∴ DG=AF,∴四边形AFDG为平行四边形.
分别为BC、AC、AB的中点,
的周长
同理, 的周长 则 的周长 故选A.
12.解析 △AGD是直角三角形.
证明:如图,连接BD,取BD的中点H,连接HF,HE,
∵F是AD的中点,∴HF是△ABD的中位线,∥∴∠1=∠3,
同理, ∥
∵AB=CD,∴HF=HE,∴∠1=∠2,∴∠3=∠2=∠EFC,
∵∠EFC=60°,∴∠3=∠EFC=∠AFG=60°,∴△AGF为等边三角形,
∵AF=FD,∴GF=FD,∴∠FGD=∠FDG=30°,∴∠AGD=30°+60°=90°,
∴△AGD是直角三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
