5.4 多边形的内角和与外角和 同步练习(含解析)
文档属性
| 名称 | 5.4 多边形的内角和与外角和 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第五章 平行四边形
4 多边形的内角和与外角和
基础过关
知识点1 多边形的内角和定理
1.一个多边形的内角和等于1260°,从它的一个顶点出发,可以作对角线的条数是( )
A.4 B.6 C.7 D.9
2.下列多边形中,内角和最大的是( )
3.小东在计算多边形的内角和时不小心多加了一个内角,得到的和为1350°,则这个多边形的边数是( )
A.7 B.8 C.9 D.10
4.如图,在五边形ABCDE中,AB∥CD,求图中x的值.
知识点2 多边形外角的定义、外角和定理
5.下列说法不正确的是( )
A.多边形的内角和随多边形边数的增加而增加
B.多边形的外角和等于360°
C.若一个多边形的内角和是外角和的2倍,则这个多边形是六边形
D.若正多边形的一个外角等于150°,则它是正十五边形
6.如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3分别是五边形的外角,则∠1+∠2+∠3等于( )
A.90° B.270° C.210° D.180°
7.从正n边形同一个顶点出发的所有对角线把正n边形分成6个三角形,则这个正n边形的每个外角的度数为___________.
8.如图,淇淇从点A出发,前进10米后向右转20°,再前进10米后又向右转20°,这样一直下去,到她第一次回到出发点A为止,她所走的路径构成了一个多边形.
(1)淇淇一共走了多少米 说明理由;
(2)求这个多边形的内角和.
9.(1)已知:n边形 如图.
求证:n边形 的内角和等于(n-2)·180°;
(2)粗心的小明在计算一个多边形的内角和时,误把一个外角也加进去了,得其和为1180°.请直接写出这个多加的外角度数及多边形的边数.
10.(1)在一个各内角都相等的多边形中,每个内角都比相邻外角的3倍大20°,求这个多边形的内角和;
(2)若将一个正九边形剪去一个角后,剩下多边形的内角和是多少
能力提升
11.如图,正五边形ABCDE中,∠CAD的度数为( )
A.72° B.45° C.36° D.35°
12.一个多边形的每个内角都等于相邻外角的4倍,则该多边形的内角和是( )
A.360° B.900° C.1440° D.1800°
13.将正六边形与正五边形按如图所示的方式摆放,公共顶点为0,且正六边形的边AB与正五边形的边DE在同一条直线上,则∠BOE的度数是( )
A.48° B.54° C.60° D.72°
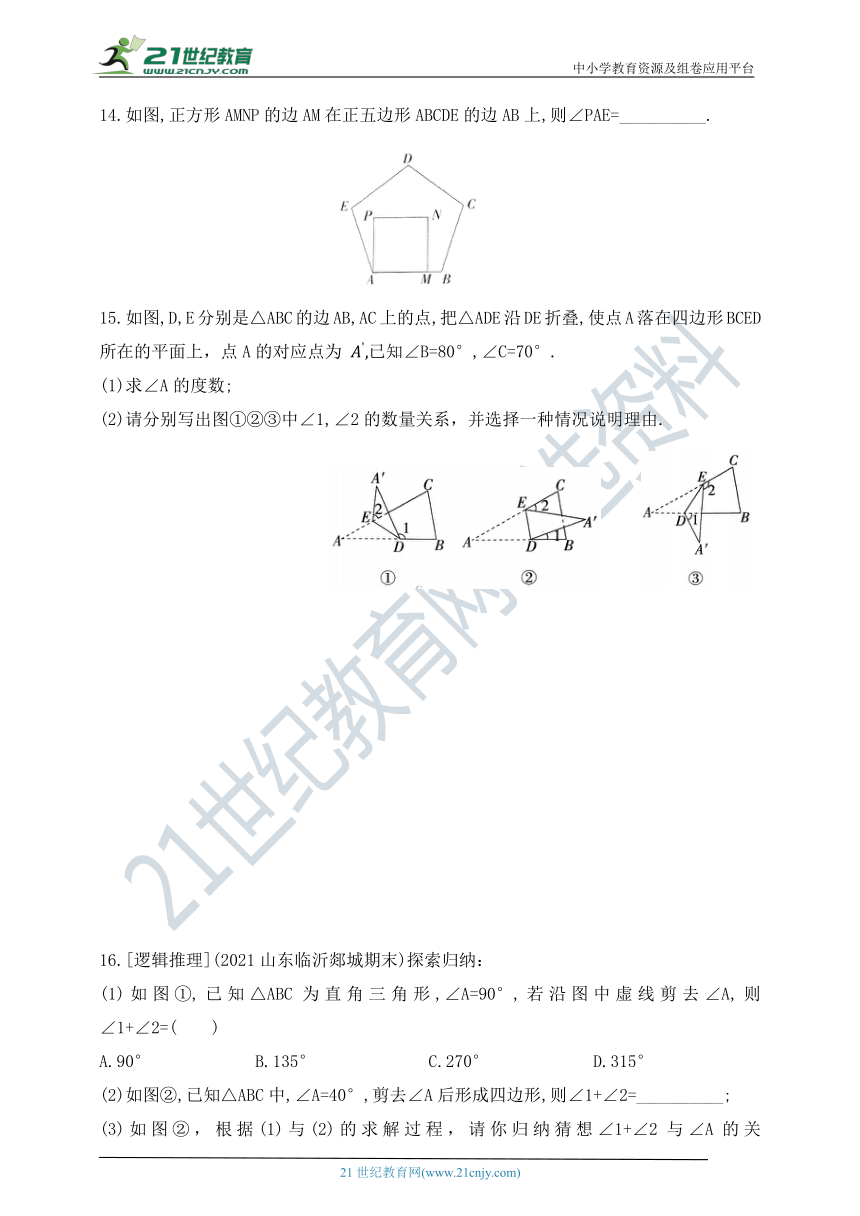
14.如图,正方形AMNP的边AM在正五边形ABCDE的边AB上,则∠PAE=__________.
15.如图,D,E分别是△ABC的边AB,AC上的点,把△ADE沿DE折叠,使点A落在四边形BCED所在的平面上,点A的对应点为 已知∠B=80°,∠C=70°.
(1)求∠A的度数;
(2)请分别写出图①②③中∠1,∠2的数量关系,并选择一种情况说明理由.
16.[逻辑推理](2021山东临沂郯城期末)探索归纳:
(1)如图①,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2=( )
A.90° B.135° C.270° D.315°
(2)如图②,已知△ABC中,∠A=40°,剪去∠A后形成四边形,则∠1+∠2=__________;
(3)如图②,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系:___________;
(4)若∠A没有被剪掉,而是把它折成如图③所示的形状,试探究∠1+∠2与∠A的关系,并说明理由.
参考答案
基础过关
1.B 设这个多边形的边数为n,则(n-2)×180°=1260°,解得n=9,∴这个多边形为九边形.从这个多边形的一个顶点出发,可以作对角线的条数是9-3=6.
2.D A项,三角形的内角和为180°;B项,四边形的内角和为360°;C项,五边形的内角和为(5-2)×180°=540°;D项,六边形的内角和为(6-2)×180°=720°.
3.C 设这个多边形的边数为n,多加的内角的度数为α,
则(n-2)·180°=1350°-α,
∵,
∵n为正整数,∴n-2=7,∴n=9,∴这个多边形的边数是9.
4.解析 ∵AB∥CD,∠C=60°,∴∠B=180°-60°=120°,
∴(5-2)×180°=x°+150°+125°+60°+120°,解得x=85.
5.D A项,多边形的内角和随多边形边数的增加而增加,故本选项说法正确;B项,多边形的外角和等于360°,故本选项说法正确;C项,若一个多边形的内角和是外角和的2倍,则这个多边形是六边形,故本选项说法正确;D项,因为360°÷150°=2.4,2.4不是整数,所以这个多边形不是正多边形,故本选项说法错误.故选D.
6.D 延长AB,DC,如图.
∵AB∥CD,∴∠4+∠5=180°,根据多边形的外角和定理可得∠1+∠2+∠3+∠4+∠5=360°,
∴∠1+∠2+∠3=360°-180°=180°.故选D.
7.答案 45°
解析 由题意可得n-2=6,则n=8,故边数为8,又因为正n边形每个外角的度数都相等,所以每个外角的度数
8.解析 (1)淇淇所经过的路线正好构成一个外角是20°的正多边形,
360°÷20°=18,18×10=180(米).
答:淇淇一共走了180米.
(2)根据题意,得(18-2)×180°=2880°.
答:这个多边形的内角和是2880°.
9.解析 (1)从n边形的一个顶点出发,可以作(n-3)条对角线,这些对角线把n边形分成的三角形个数为n-3+1=n-2,
∵这(n-2)个三角形的内角和都等于180°,∴n边形的内角和是(n-2)·180°.
(2)设多边形的边数为n,多加的外角的度数为α,则(n-2)·180°=1180°-α,
∵1180°=6×180°+100°,内角和应是180°的倍数,0°<α<180°,
∴小明多加的一个外角的度数为100°,n-2=6,
∴该多边形的边数是6+2=8.
10.解析 (1)设多边形的每个外角为α°,则与其相邻的内角为(3α+20)°,
由题意,得(3a+20)+α=180,解得α=40,即多边形的每个外角为40°.
∵多边形的外角和为360°,∴多边形的边数为360°÷40°=9,
∴这个多边形的内角和为(9-2)×180°=1260°.
(2)将一个正九边形剪去一个角后,边数可能增加了1条,也可能减少了1条,或者不变.
当截线为经过2个顶点的直线时,多边形的边数减少了1条,此时内角和=(9-1-2)×180°=1080°;
当截线为只经过一个顶点和一条边的直线时,多边形的边数不变,此时内角和=(9-2)×180°=1260°;
当截线为经过相邻2条边的一条直线时(不经过顶点),多边形的边数增加了一条,此时内角和=(9+1-2)×180°=1 440°.
综上,将一个正九边形剪去一个角后,剩下多边形的内角和是1080°或1260°或1440°.
能力提升
11.C 正五边形ABCDE的内角和=(5-2)×180°=540°,则 又∵AB=AE=BC=-108°)= 36°,
∴∠CAD=108°-36°-36°=36°,故选C.
12.C 设多边形的每个外角为x,则与其相邻的内角为4x,由题意得,4x+x=180°,解得x=36°.因为360°÷36°=10,所以这个多边形的边数为10,则该多边形的内角和为(10-2)×180°=1440°.故选C.
13.A 由题意得 ∴∠BOE=180°-72°-60°=48°,故选A.
14.答案 18°
解析 ∵五边形ABCDE为正五边形,
∵四边形AMNP为正方形,∴∠PAM=90°,∴∠PAE=∠EAB-∠PAM=108°-90°=18°.
15.解析 (1)∵∠B=80°,∠C=70°,
∴∠A=180°-(∠B+∠C)=180°-(80°+70°)=30°.
(2)题图①:∠1-∠2=60°.
题图②:∠1+∠2=60°.
题图③:∠2-∠1=60°.
当选择题图①时,如图,
∵把△ADE沿DE折叠,使点A落在四边形BCED所在的平面上,点A的对应点为
∵∠1+∠3+∠B+∠C=360°,∴∠1+150°-∠2+80°+70°=360°,∴∠1-∠2=60°.
当选择题图②时,∵把△ADE沿DE折叠,使点A落在四边形BCED所在的平面上,点A的对应点为
当选择题图③时,方法同题图①,可得∠2-∠1=60°.
16.解析 (1)如图,∵四边形的内角和为360°,直角三角形中两个锐角的和为90°,∴∠1+∠2=360°-(∠B+∠C)=360°-(180°-∠A)=180°+∠A=270°.故选C.
(2) ∠1+∠2=180°+40°=220°.
(3)∠1+∠2与∠A的关系是∠1+∠2=180°+∠A.
(4)∠1+∠2=2∠A.
理由:∵△EFP是由△EFA折叠得到的,∴∠AFE=∠PFE,∠AEF=∠PEF,
∴∠1=180°-2∠AFE,∠2=180°-2∠AEF,∴∠1+∠2=360°-2(∠AFE+∠AEF),
又∵∠AFE+∠AEF=180°-∠A,∴∠1+∠2=360°-2(180°-∠A)=2∠A.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 平行四边形
4 多边形的内角和与外角和
基础过关
知识点1 多边形的内角和定理
1.一个多边形的内角和等于1260°,从它的一个顶点出发,可以作对角线的条数是( )
A.4 B.6 C.7 D.9
2.下列多边形中,内角和最大的是( )
3.小东在计算多边形的内角和时不小心多加了一个内角,得到的和为1350°,则这个多边形的边数是( )
A.7 B.8 C.9 D.10
4.如图,在五边形ABCDE中,AB∥CD,求图中x的值.
知识点2 多边形外角的定义、外角和定理
5.下列说法不正确的是( )
A.多边形的内角和随多边形边数的增加而增加
B.多边形的外角和等于360°
C.若一个多边形的内角和是外角和的2倍,则这个多边形是六边形
D.若正多边形的一个外角等于150°,则它是正十五边形
6.如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3分别是五边形的外角,则∠1+∠2+∠3等于( )
A.90° B.270° C.210° D.180°
7.从正n边形同一个顶点出发的所有对角线把正n边形分成6个三角形,则这个正n边形的每个外角的度数为___________.
8.如图,淇淇从点A出发,前进10米后向右转20°,再前进10米后又向右转20°,这样一直下去,到她第一次回到出发点A为止,她所走的路径构成了一个多边形.
(1)淇淇一共走了多少米 说明理由;
(2)求这个多边形的内角和.
9.(1)已知:n边形 如图.
求证:n边形 的内角和等于(n-2)·180°;
(2)粗心的小明在计算一个多边形的内角和时,误把一个外角也加进去了,得其和为1180°.请直接写出这个多加的外角度数及多边形的边数.
10.(1)在一个各内角都相等的多边形中,每个内角都比相邻外角的3倍大20°,求这个多边形的内角和;
(2)若将一个正九边形剪去一个角后,剩下多边形的内角和是多少
能力提升
11.如图,正五边形ABCDE中,∠CAD的度数为( )
A.72° B.45° C.36° D.35°
12.一个多边形的每个内角都等于相邻外角的4倍,则该多边形的内角和是( )
A.360° B.900° C.1440° D.1800°
13.将正六边形与正五边形按如图所示的方式摆放,公共顶点为0,且正六边形的边AB与正五边形的边DE在同一条直线上,则∠BOE的度数是( )
A.48° B.54° C.60° D.72°
14.如图,正方形AMNP的边AM在正五边形ABCDE的边AB上,则∠PAE=__________.
15.如图,D,E分别是△ABC的边AB,AC上的点,把△ADE沿DE折叠,使点A落在四边形BCED所在的平面上,点A的对应点为 已知∠B=80°,∠C=70°.
(1)求∠A的度数;
(2)请分别写出图①②③中∠1,∠2的数量关系,并选择一种情况说明理由.
16.[逻辑推理](2021山东临沂郯城期末)探索归纳:
(1)如图①,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2=( )
A.90° B.135° C.270° D.315°
(2)如图②,已知△ABC中,∠A=40°,剪去∠A后形成四边形,则∠1+∠2=__________;
(3)如图②,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系:___________;
(4)若∠A没有被剪掉,而是把它折成如图③所示的形状,试探究∠1+∠2与∠A的关系,并说明理由.
参考答案
基础过关
1.B 设这个多边形的边数为n,则(n-2)×180°=1260°,解得n=9,∴这个多边形为九边形.从这个多边形的一个顶点出发,可以作对角线的条数是9-3=6.
2.D A项,三角形的内角和为180°;B项,四边形的内角和为360°;C项,五边形的内角和为(5-2)×180°=540°;D项,六边形的内角和为(6-2)×180°=720°.
3.C 设这个多边形的边数为n,多加的内角的度数为α,
则(n-2)·180°=1350°-α,
∵,
∵n为正整数,∴n-2=7,∴n=9,∴这个多边形的边数是9.
4.解析 ∵AB∥CD,∠C=60°,∴∠B=180°-60°=120°,
∴(5-2)×180°=x°+150°+125°+60°+120°,解得x=85.
5.D A项,多边形的内角和随多边形边数的增加而增加,故本选项说法正确;B项,多边形的外角和等于360°,故本选项说法正确;C项,若一个多边形的内角和是外角和的2倍,则这个多边形是六边形,故本选项说法正确;D项,因为360°÷150°=2.4,2.4不是整数,所以这个多边形不是正多边形,故本选项说法错误.故选D.
6.D 延长AB,DC,如图.
∵AB∥CD,∴∠4+∠5=180°,根据多边形的外角和定理可得∠1+∠2+∠3+∠4+∠5=360°,
∴∠1+∠2+∠3=360°-180°=180°.故选D.
7.答案 45°
解析 由题意可得n-2=6,则n=8,故边数为8,又因为正n边形每个外角的度数都相等,所以每个外角的度数
8.解析 (1)淇淇所经过的路线正好构成一个外角是20°的正多边形,
360°÷20°=18,18×10=180(米).
答:淇淇一共走了180米.
(2)根据题意,得(18-2)×180°=2880°.
答:这个多边形的内角和是2880°.
9.解析 (1)从n边形的一个顶点出发,可以作(n-3)条对角线,这些对角线把n边形分成的三角形个数为n-3+1=n-2,
∵这(n-2)个三角形的内角和都等于180°,∴n边形的内角和是(n-2)·180°.
(2)设多边形的边数为n,多加的外角的度数为α,则(n-2)·180°=1180°-α,
∵1180°=6×180°+100°,内角和应是180°的倍数,0°<α<180°,
∴小明多加的一个外角的度数为100°,n-2=6,
∴该多边形的边数是6+2=8.
10.解析 (1)设多边形的每个外角为α°,则与其相邻的内角为(3α+20)°,
由题意,得(3a+20)+α=180,解得α=40,即多边形的每个外角为40°.
∵多边形的外角和为360°,∴多边形的边数为360°÷40°=9,
∴这个多边形的内角和为(9-2)×180°=1260°.
(2)将一个正九边形剪去一个角后,边数可能增加了1条,也可能减少了1条,或者不变.
当截线为经过2个顶点的直线时,多边形的边数减少了1条,此时内角和=(9-1-2)×180°=1080°;
当截线为只经过一个顶点和一条边的直线时,多边形的边数不变,此时内角和=(9-2)×180°=1260°;
当截线为经过相邻2条边的一条直线时(不经过顶点),多边形的边数增加了一条,此时内角和=(9+1-2)×180°=1 440°.
综上,将一个正九边形剪去一个角后,剩下多边形的内角和是1080°或1260°或1440°.
能力提升
11.C 正五边形ABCDE的内角和=(5-2)×180°=540°,则 又∵AB=AE=BC=-108°)= 36°,
∴∠CAD=108°-36°-36°=36°,故选C.
12.C 设多边形的每个外角为x,则与其相邻的内角为4x,由题意得,4x+x=180°,解得x=36°.因为360°÷36°=10,所以这个多边形的边数为10,则该多边形的内角和为(10-2)×180°=1440°.故选C.
13.A 由题意得 ∴∠BOE=180°-72°-60°=48°,故选A.
14.答案 18°
解析 ∵五边形ABCDE为正五边形,
∵四边形AMNP为正方形,∴∠PAM=90°,∴∠PAE=∠EAB-∠PAM=108°-90°=18°.
15.解析 (1)∵∠B=80°,∠C=70°,
∴∠A=180°-(∠B+∠C)=180°-(80°+70°)=30°.
(2)题图①:∠1-∠2=60°.
题图②:∠1+∠2=60°.
题图③:∠2-∠1=60°.
当选择题图①时,如图,
∵把△ADE沿DE折叠,使点A落在四边形BCED所在的平面上,点A的对应点为
∵∠1+∠3+∠B+∠C=360°,∴∠1+150°-∠2+80°+70°=360°,∴∠1-∠2=60°.
当选择题图②时,∵把△ADE沿DE折叠,使点A落在四边形BCED所在的平面上,点A的对应点为
当选择题图③时,方法同题图①,可得∠2-∠1=60°.
16.解析 (1)如图,∵四边形的内角和为360°,直角三角形中两个锐角的和为90°,∴∠1+∠2=360°-(∠B+∠C)=360°-(180°-∠A)=180°+∠A=270°.故选C.
(2) ∠1+∠2=180°+40°=220°.
(3)∠1+∠2与∠A的关系是∠1+∠2=180°+∠A.
(4)∠1+∠2=2∠A.
理由:∵△EFP是由△EFA折叠得到的,∴∠AFE=∠PFE,∠AEF=∠PEF,
∴∠1=180°-2∠AFE,∠2=180°-2∠AEF,∴∠1+∠2=360°-2(∠AFE+∠AEF),
又∵∠AFE+∠AEF=180°-∠A,∴∠1+∠2=360°-2(180°-∠A)=2∠A.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
