第五章 平行四边形 综合测试题(含解析)
文档属性
| 名称 | 第五章 平行四边形 综合测试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 09:37:07 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第五章综合测试题
(满分:100分 时间:60分钟)
一、选择题(每小题3分,共30分)
1.一个凸多边形的内角和与外角和之比为2:1,则这个多边形的边数为( )
A.5 B.6 C.7 D.8
2.如图,在平行四边形ABCD中,AE⊥CD,若∠B=70°,则∠DAE的度数是( )
A.20° B.15° C.30° D.70°
3.在平行四边形ABCD中,对角线AC与BD相交于点O,若AC=6,BD=8,则AB的取值范围是( )
4.如图,在四边形ABCD中,AB=CD,BC=AD,若∠D=120°,则∠C的度数为( )
A.60° B.70° C.80° D.90°
5.若平行四边形ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,△DOE的周长为15,则BD的长为 ( )
A.18 B.16 C.14 D.12
6.如图,△ABC中,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,连接MN.若 则△ABC的周长为( )
A.17 B.18 C.19 D.20
7.在四边形ABCD中,对角线AC、BD相交于点O,在下列条件中:①AB∥CD,AD∥BC;②AB=CD,
AD=BC;③AB∥CD,AD=BC;④OA=OC,OB=OD;⑤AB∥CD,∠BAD=∠BCD,能够判定四边形ABCD是平行四边形的个数为( )
A.2 B.3 C.4 D.5
8.如图,正五边形ABCDE的对角线AC、BD交于点P,那么∠APD=( )
A.96° B.100° C.108° D.115°
9.如图所示,M是 ABCD的边AD上任意一点,若△CMB的面积为S,△CDM的面积为S ,△ABM的面积为S ,则下列关于S, 的关系中,正确的是( )
的关系无法确定
10.如图,在△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形,下列结论中:①AB⊥AC;②四边形AEFD是平行四边形;③∠DFE=150°; ④错误的个数是( )
A.1 B.2 C.3 D.4
二、填空题(每小题3分,共24分)
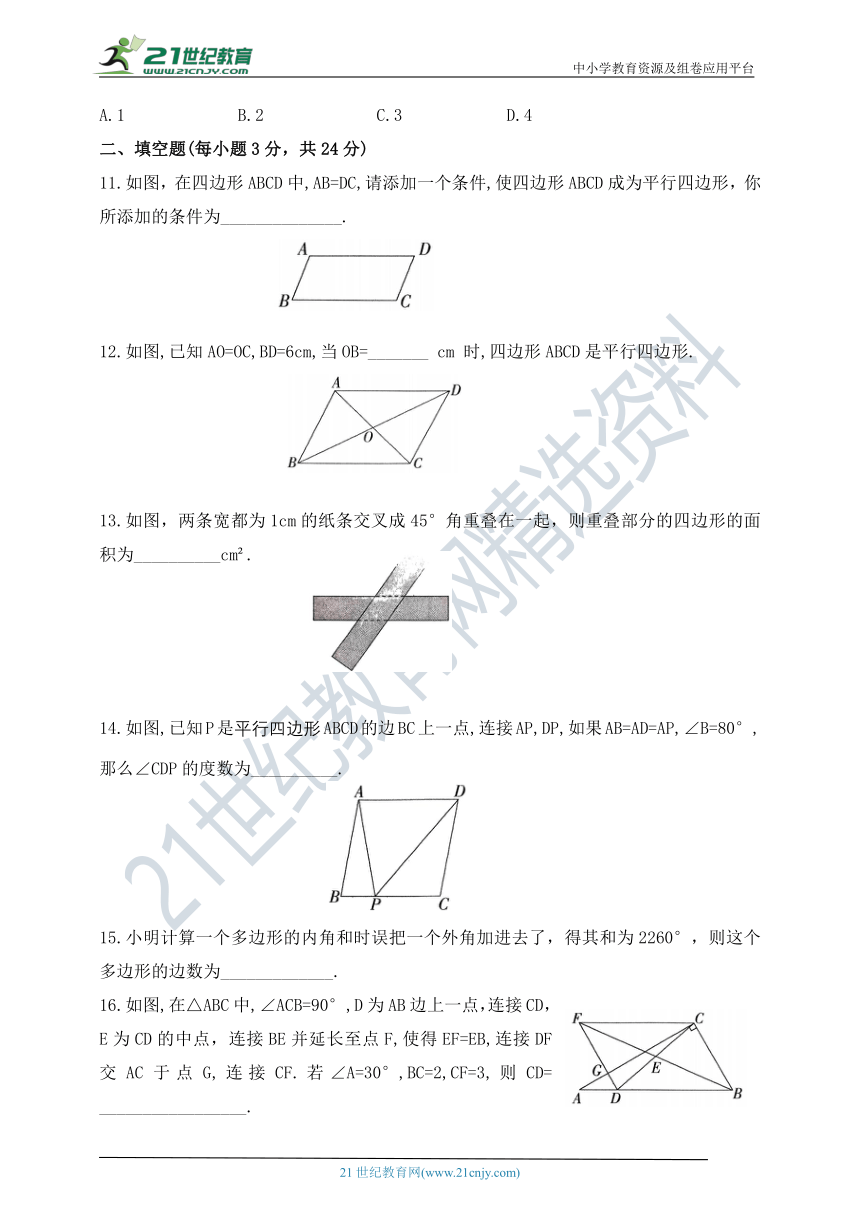
11.如图,在四边形ABCD中,AB=DC,请添加一个条件,使四边形ABCD成为平行四边形,你所添加的条件为______________.
12.如图,已知AO=OC,BD=6cm,当OB=_______ cm 时,四边形ABCD是平行四边形.
13.如图,两条宽都为1cm的纸条交叉成45°角重叠在一起,则重叠部分的四边形的面积为__________cm .
14.如图,已知P是平行四边形ABCD的边BC上一点,连接AP,DP,如果AB=AD=AP,∠B=80°,那么∠CDP的度数为__________.
15.小明计算一个多边形的内角和时误把一个外角加进去了,得其和为2260°,则这个多边形的边数为_____________.
16.如图,在△ABC中,∠ACB=90°,D为AB边上一点,连接CD,E为CD的中点,连接BE并延长至点F,使得EF=EB,连接DF交AC于点G,连接CF.若∠A=30°,BC=2,CF=3,则CD= _________________.
17.如图,在平行四边形ABCD中,E在AC上,AE=2EC,F在AB上,BF=2AF,若 则
18.如图,在平面直角坐标系中,已知点A(4,0),点B(-3,2),点C(0,2),点P从点B出发,以每秒2个单位的速度沿射线BC运动,点Q从点A出发,开始以每秒1个单位的速度向原点O运动,到达原点后立即以每秒3个单位的速度沿射线OA运动,若P,Q两点同时出发,设运动时间为t秒,若以点A,Q,C,P为顶点的四边形为平行四边形,则t等于______________.
三、解答题(共46分)
19. (10分)已知一个正多边形的每个内角都等于相邻外角的 求这个正多边形的边数.
20. (12分)如图,在平行四边形ABCD中,点F是AD的中点,连接CF并延长,交BA的延长线于点E.
(1)求证:AB=AE;
(2)若BC=2AE,∠E=31°,求∠DAB的度数.
21.(12分)如图,在平行四边形ABCD中,∠ABC的平分线与CD的延长线交于点E,与AD交于点F,且点F恰好为边AD的中点,连接AE.
(1)求证:四边形ABDE是平行四边形;
(2)若AG⊥BE于点G,BC=6,AG=2,求EF的长.
22. (12分)在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DE∥AC交直线AB于点E,DF∥AB交直线AC于点F.
(1)当点D在边BC上时,如图①,求证:DE+DF=AC;
(2)当点D在边BC的延长线上时,如图②,当点D在边BC的反向延长线上时,如图③,请分别写出图②③中DE、DF、AC之间的等量关系(不需要证明);
(3)若AC=10,DE=7,求DF的长.
参考答案
1.B 设多边形的边数为n,由题意得(n-2)·180°=360°×2,解得n=6,故选B.
2.A ∵四边形ABCD是平行四边形,∴∠D=∠B=70°,∵AE⊥CD,∴∠DAE=90°-∠D=20°,故选A.
3.A ∵四边形ABCD是平行四边形,AC=6,BD=8,∴OA=3,OB=4.在△AOB中,
4.A ∵AB=CD,BC=AD,∴四边形ABCD是平行四边形,
∴AD//BC,∴∠C+∠D=180°,∵∠D=120°,∴∠C=60°.故选A.
5.D ∵四边形ABCD是平行四边形,其周长为36,∴AD+CD=18,BD=20D,AC=2AO,
又∵点E是CD的中点,∴OE是△ACD的中位线,
∵△DOE的周长为15,
6.A 在△BNA和△BNE中∴△BNA≌△BNE(ASA),∴BE=BA,AN=NE,
同理,CD=CA,AM=MD,
∵BE+CD-BC=DE,∴AB+AC=BC+DE=10,
∴△ABC的周长=AB+AC+BC=10+7=17,故选A.
7.C ①若AB∥CD,AD∥BC,则四边形ABCD有两组对边分别平行,可判定四边形ABCD为平行四边形;
②若AB=CD,AD=BC,则四边形ABCD有两组对边分别相等,可判定四边形ABCD为平行四边形;
③由AB∥CD,AD=BC,不能判定四边形ABCD为平行四边形;
④若OA=OC,OB=OD,则四边形ABCD的对角线互相平分,可判定四边形ABCD为平行四边形;
⑤∵AB∥CD,∴∠BAD+∠ADC=180°,∵∠BAD=∠BCD,∴∠ADC+∠BCD=180°,∴AD∥BC,∴四边形ABCD为平行四边形.故选C.
8.C ∵五边形ABCDE为正五边形,∴AB=BC=CD,∠ABC=∠BCD=108°,
∴∠APD=∠BPC=180°-∠CBD-∠BCA=180°-36°-36°=108°.故选C.
9.B 过M作ME⊥BC于点E(图略).
∵四边形ABCD是平行四边形,∴AD=BC.
∵△CMB的面积 的面积S =的面积 的关系是 故选B.
∴△ABC是直角三角形,∠BAC=90°,∴AB⊥AC,故①正确;
∵△ABD,△ACE都是等边三角形,∴∠DAB=∠EAC=60°,∴∠DAE=360°-90°-60°-60°=150°,∵△ABD和△FBC都是等边三角形,∴BD=BA,BF=BC,∠DBF+∠FBA=∠ABC+
∠ABF=60°,∴∠DBF=∠ABC,
在△ABC与△DBF中,∴△ABC≌△DBF(SAS),∴AC=DF=AE=4,
同理可证△ABC≌△EFC(SAS),∴AB=EF=AD=3,∴四边形AEFD是平行四边形(②正确),
∴∠DFE=∠DAE=150°,故③正确;
如图,过A作AG⊥DF于G,则∠AGD=90°,
∵四边形AEFD是平行四边形,∴AD∥EF,∴∠FDA=180°-∠DFE=180°-150°=30°,
故④错误.
∴错误的个数是1,故选A.
11.答案 AB∥DC(答案不唯一)
解析 添加的条件可以为AB∥DC.
理由:∵AB=DC,AB∥DC,∴四边形ABCD为平行四边形.
12.答案 3
解析 当OB=3cm时,四边形ABCD是平行四边形.
理由:∵BD=6cm,OB=3cm,∴OD=BD-OB=3 cm,∴OD=OB,又∵AO=OC,∴四边形ABCD是平行四边形.
13.答案
解析 如图,过点A作AF⊥BC于F,过点C作CE⊥AB于E,
由题意可得AB∥CD,AD∥BC,AF=CE=1cm,∴四边形ABCD是平行四边形,
∵∠ABC=45°,AF⊥BC,
∴重叠部分的四边形的面积
14.答案 30°
解析 ∵四边形ABCD是平行四边形,∴∠ADC=∠B=80°,AD∥BC,∴∠PAD=∠APB,
∵AB=AP,∴∠APB=∠B=80°,∴∠PAD=80°,
∵AP=AD,∴∠ADP=∠APD=(180°-80°)÷2=50°,
∴∠CDP=∠ADC-∠ADP=80°-50°=30°.
15.答案 14
解析 设这个多边形的边数为n,多加的一个外角的度数为α,则(n-2)·180°=2260°-α,
∵内角和是180°的倍数,,且2260°=12×180°+100°,
∴小明多加的一个外角的度数为100°,这个多边形的边数为12+2=14.
16.答案
解析 ∵E为CD的中点,∴CE=DE.
又∵EF=BE,∴四边形DBCF是平行四边形.∴CF∥AB,DF∥BC,DF=BC=2.
∴∠FCG=∠A=30°,∠CGF=∠CGD=∠ACB=90°.
在Rt△FCG中,CF=3,
∴在Rt△DCG中,
17.答案 18
解析
,
∵四边形ABCD是平行四边形,∴AB=CD,BC=AD,又∵AC=CA,
18.答案 1或3或13
解析 ∵A(4,0),B(-3,2),C(0,2),∴OA=4,BC=3,BC∥x轴,
∵PC∥AQ,∴当PC=AQ时,以点A,Q,C,P为顶点的四边形为平行四边形,
当 时,BP=2t,PC=3-2t,AQ=t,令3-2t=t,解得t=1;
当 时,BP=2t,PC=2t-3,AQ=t,
令2t-3=t,解得t=3;
当 时,BP=2t,PC=2t-3,OQ=3(t-4),AQ=4-3(t-4) ,
令2t-3=4-3(t-4),解得 (舍去);
当 时,BP=2t,PC=2t-3,OQ=3(t-4),AQ=3(t-4) -4,
令2t-3=3(t-4)-4,解得t=13.
综上所述,当t=1或3或13时,以点A,Q,C,P为顶点的四边形为平行四边形.
19.解析 设这个正多边形的边数为n.
∵正多边形的每个内角都等于相邻外角的 ∴这个正多边形的内角和等于外角和的
解得n=5.
故这个正多边形的边数为5.
20.解析 (1)证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,BC=AD,∴∠E=∠DCF,
∵点F是AD的中点,∴AF=DF,
又∵∠EFA=∠CFD,∴△AFE≌△DFC(AAS),∴CD=AE,∴AB=AE.
(2) ∵AB=AE,BC=2AE,∴BC=BE,∴∠BCE=∠E=31°.
∵AB∥CD,∴∠ECD=∠E=31°,
∵∠DCB=∠BCE+∠ECD=62°,∠DAB=∠DCB,∴∠DAB=62°.
21.解析 (1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠ABE=∠BEC,
∵点F恰好为边AD的中点,∴AF=DF,
又∵∠AFB=∠DFE,∴△ABF≌△DEF(AAS),∴DE=AB,
又∵DE∥AB,∴四边形ABDE是平行四边形.
(2)∵四边形ABCD是平行四边形,∴AD∥CB,∴∠AFB=∠CBF,
∵BE平分∠ABC,∴∠ABE=∠CBE,∴∠AFB=∠ABF,∴AF=AB,又AG⊥BE,∴BG=FG.
∵AF=DF,AD=BC=6,∴AB=AF=3,
∵Rt△ABG中,
22.解析 (1)证明:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,∠FDC=∠B,∴DE=AF,
又∵AB=AC,∴∠B=∠C,∴∠FDC=∠C,∴DF=FC,∴DE+DF=AF+FC=AC.
(2)当点D在边BC的延长线上时,DE-DF=AC.
当点D在边BC的反向延长线上时,DF-DE=AC.
(3)当点D在边BC上时,DF=AC-DE=10-7=3.
当点D在边BC的反向延长线上时,DF=AC+DE=10+7=17.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章综合测试题
(满分:100分 时间:60分钟)
一、选择题(每小题3分,共30分)
1.一个凸多边形的内角和与外角和之比为2:1,则这个多边形的边数为( )
A.5 B.6 C.7 D.8
2.如图,在平行四边形ABCD中,AE⊥CD,若∠B=70°,则∠DAE的度数是( )
A.20° B.15° C.30° D.70°
3.在平行四边形ABCD中,对角线AC与BD相交于点O,若AC=6,BD=8,则AB的取值范围是( )
4.如图,在四边形ABCD中,AB=CD,BC=AD,若∠D=120°,则∠C的度数为( )
A.60° B.70° C.80° D.90°
5.若平行四边形ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,△DOE的周长为15,则BD的长为 ( )
A.18 B.16 C.14 D.12
6.如图,△ABC中,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,连接MN.若 则△ABC的周长为( )
A.17 B.18 C.19 D.20
7.在四边形ABCD中,对角线AC、BD相交于点O,在下列条件中:①AB∥CD,AD∥BC;②AB=CD,
AD=BC;③AB∥CD,AD=BC;④OA=OC,OB=OD;⑤AB∥CD,∠BAD=∠BCD,能够判定四边形ABCD是平行四边形的个数为( )
A.2 B.3 C.4 D.5
8.如图,正五边形ABCDE的对角线AC、BD交于点P,那么∠APD=( )
A.96° B.100° C.108° D.115°
9.如图所示,M是 ABCD的边AD上任意一点,若△CMB的面积为S,△CDM的面积为S ,△ABM的面积为S ,则下列关于S, 的关系中,正确的是( )
的关系无法确定
10.如图,在△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形,下列结论中:①AB⊥AC;②四边形AEFD是平行四边形;③∠DFE=150°; ④错误的个数是( )
A.1 B.2 C.3 D.4
二、填空题(每小题3分,共24分)
11.如图,在四边形ABCD中,AB=DC,请添加一个条件,使四边形ABCD成为平行四边形,你所添加的条件为______________.
12.如图,已知AO=OC,BD=6cm,当OB=_______ cm 时,四边形ABCD是平行四边形.
13.如图,两条宽都为1cm的纸条交叉成45°角重叠在一起,则重叠部分的四边形的面积为__________cm .
14.如图,已知P是平行四边形ABCD的边BC上一点,连接AP,DP,如果AB=AD=AP,∠B=80°,那么∠CDP的度数为__________.
15.小明计算一个多边形的内角和时误把一个外角加进去了,得其和为2260°,则这个多边形的边数为_____________.
16.如图,在△ABC中,∠ACB=90°,D为AB边上一点,连接CD,E为CD的中点,连接BE并延长至点F,使得EF=EB,连接DF交AC于点G,连接CF.若∠A=30°,BC=2,CF=3,则CD= _________________.
17.如图,在平行四边形ABCD中,E在AC上,AE=2EC,F在AB上,BF=2AF,若 则
18.如图,在平面直角坐标系中,已知点A(4,0),点B(-3,2),点C(0,2),点P从点B出发,以每秒2个单位的速度沿射线BC运动,点Q从点A出发,开始以每秒1个单位的速度向原点O运动,到达原点后立即以每秒3个单位的速度沿射线OA运动,若P,Q两点同时出发,设运动时间为t秒,若以点A,Q,C,P为顶点的四边形为平行四边形,则t等于______________.
三、解答题(共46分)
19. (10分)已知一个正多边形的每个内角都等于相邻外角的 求这个正多边形的边数.
20. (12分)如图,在平行四边形ABCD中,点F是AD的中点,连接CF并延长,交BA的延长线于点E.
(1)求证:AB=AE;
(2)若BC=2AE,∠E=31°,求∠DAB的度数.
21.(12分)如图,在平行四边形ABCD中,∠ABC的平分线与CD的延长线交于点E,与AD交于点F,且点F恰好为边AD的中点,连接AE.
(1)求证:四边形ABDE是平行四边形;
(2)若AG⊥BE于点G,BC=6,AG=2,求EF的长.
22. (12分)在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DE∥AC交直线AB于点E,DF∥AB交直线AC于点F.
(1)当点D在边BC上时,如图①,求证:DE+DF=AC;
(2)当点D在边BC的延长线上时,如图②,当点D在边BC的反向延长线上时,如图③,请分别写出图②③中DE、DF、AC之间的等量关系(不需要证明);
(3)若AC=10,DE=7,求DF的长.
参考答案
1.B 设多边形的边数为n,由题意得(n-2)·180°=360°×2,解得n=6,故选B.
2.A ∵四边形ABCD是平行四边形,∴∠D=∠B=70°,∵AE⊥CD,∴∠DAE=90°-∠D=20°,故选A.
3.A ∵四边形ABCD是平行四边形,AC=6,BD=8,∴OA=3,OB=4.在△AOB中,
4.A ∵AB=CD,BC=AD,∴四边形ABCD是平行四边形,
∴AD//BC,∴∠C+∠D=180°,∵∠D=120°,∴∠C=60°.故选A.
5.D ∵四边形ABCD是平行四边形,其周长为36,∴AD+CD=18,BD=20D,AC=2AO,
又∵点E是CD的中点,∴OE是△ACD的中位线,
∵△DOE的周长为15,
6.A 在△BNA和△BNE中∴△BNA≌△BNE(ASA),∴BE=BA,AN=NE,
同理,CD=CA,AM=MD,
∵BE+CD-BC=DE,∴AB+AC=BC+DE=10,
∴△ABC的周长=AB+AC+BC=10+7=17,故选A.
7.C ①若AB∥CD,AD∥BC,则四边形ABCD有两组对边分别平行,可判定四边形ABCD为平行四边形;
②若AB=CD,AD=BC,则四边形ABCD有两组对边分别相等,可判定四边形ABCD为平行四边形;
③由AB∥CD,AD=BC,不能判定四边形ABCD为平行四边形;
④若OA=OC,OB=OD,则四边形ABCD的对角线互相平分,可判定四边形ABCD为平行四边形;
⑤∵AB∥CD,∴∠BAD+∠ADC=180°,∵∠BAD=∠BCD,∴∠ADC+∠BCD=180°,∴AD∥BC,∴四边形ABCD为平行四边形.故选C.
8.C ∵五边形ABCDE为正五边形,∴AB=BC=CD,∠ABC=∠BCD=108°,
∴∠APD=∠BPC=180°-∠CBD-∠BCA=180°-36°-36°=108°.故选C.
9.B 过M作ME⊥BC于点E(图略).
∵四边形ABCD是平行四边形,∴AD=BC.
∵△CMB的面积 的面积S =的面积 的关系是 故选B.
∴△ABC是直角三角形,∠BAC=90°,∴AB⊥AC,故①正确;
∵△ABD,△ACE都是等边三角形,∴∠DAB=∠EAC=60°,∴∠DAE=360°-90°-60°-60°=150°,∵△ABD和△FBC都是等边三角形,∴BD=BA,BF=BC,∠DBF+∠FBA=∠ABC+
∠ABF=60°,∴∠DBF=∠ABC,
在△ABC与△DBF中,∴△ABC≌△DBF(SAS),∴AC=DF=AE=4,
同理可证△ABC≌△EFC(SAS),∴AB=EF=AD=3,∴四边形AEFD是平行四边形(②正确),
∴∠DFE=∠DAE=150°,故③正确;
如图,过A作AG⊥DF于G,则∠AGD=90°,
∵四边形AEFD是平行四边形,∴AD∥EF,∴∠FDA=180°-∠DFE=180°-150°=30°,
故④错误.
∴错误的个数是1,故选A.
11.答案 AB∥DC(答案不唯一)
解析 添加的条件可以为AB∥DC.
理由:∵AB=DC,AB∥DC,∴四边形ABCD为平行四边形.
12.答案 3
解析 当OB=3cm时,四边形ABCD是平行四边形.
理由:∵BD=6cm,OB=3cm,∴OD=BD-OB=3 cm,∴OD=OB,又∵AO=OC,∴四边形ABCD是平行四边形.
13.答案
解析 如图,过点A作AF⊥BC于F,过点C作CE⊥AB于E,
由题意可得AB∥CD,AD∥BC,AF=CE=1cm,∴四边形ABCD是平行四边形,
∵∠ABC=45°,AF⊥BC,
∴重叠部分的四边形的面积
14.答案 30°
解析 ∵四边形ABCD是平行四边形,∴∠ADC=∠B=80°,AD∥BC,∴∠PAD=∠APB,
∵AB=AP,∴∠APB=∠B=80°,∴∠PAD=80°,
∵AP=AD,∴∠ADP=∠APD=(180°-80°)÷2=50°,
∴∠CDP=∠ADC-∠ADP=80°-50°=30°.
15.答案 14
解析 设这个多边形的边数为n,多加的一个外角的度数为α,则(n-2)·180°=2260°-α,
∵内角和是180°的倍数,,且2260°=12×180°+100°,
∴小明多加的一个外角的度数为100°,这个多边形的边数为12+2=14.
16.答案
解析 ∵E为CD的中点,∴CE=DE.
又∵EF=BE,∴四边形DBCF是平行四边形.∴CF∥AB,DF∥BC,DF=BC=2.
∴∠FCG=∠A=30°,∠CGF=∠CGD=∠ACB=90°.
在Rt△FCG中,CF=3,
∴在Rt△DCG中,
17.答案 18
解析
,
∵四边形ABCD是平行四边形,∴AB=CD,BC=AD,又∵AC=CA,
18.答案 1或3或13
解析 ∵A(4,0),B(-3,2),C(0,2),∴OA=4,BC=3,BC∥x轴,
∵PC∥AQ,∴当PC=AQ时,以点A,Q,C,P为顶点的四边形为平行四边形,
当 时,BP=2t,PC=3-2t,AQ=t,令3-2t=t,解得t=1;
当 时,BP=2t,PC=2t-3,AQ=t,
令2t-3=t,解得t=3;
当 时,BP=2t,PC=2t-3,OQ=3(t-4),AQ=4-3(t-4) ,
令2t-3=4-3(t-4),解得 (舍去);
当 时,BP=2t,PC=2t-3,OQ=3(t-4),AQ=3(t-4) -4,
令2t-3=3(t-4)-4,解得t=13.
综上所述,当t=1或3或13时,以点A,Q,C,P为顶点的四边形为平行四边形.
19.解析 设这个正多边形的边数为n.
∵正多边形的每个内角都等于相邻外角的 ∴这个正多边形的内角和等于外角和的
解得n=5.
故这个正多边形的边数为5.
20.解析 (1)证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,BC=AD,∴∠E=∠DCF,
∵点F是AD的中点,∴AF=DF,
又∵∠EFA=∠CFD,∴△AFE≌△DFC(AAS),∴CD=AE,∴AB=AE.
(2) ∵AB=AE,BC=2AE,∴BC=BE,∴∠BCE=∠E=31°.
∵AB∥CD,∴∠ECD=∠E=31°,
∵∠DCB=∠BCE+∠ECD=62°,∠DAB=∠DCB,∴∠DAB=62°.
21.解析 (1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠ABE=∠BEC,
∵点F恰好为边AD的中点,∴AF=DF,
又∵∠AFB=∠DFE,∴△ABF≌△DEF(AAS),∴DE=AB,
又∵DE∥AB,∴四边形ABDE是平行四边形.
(2)∵四边形ABCD是平行四边形,∴AD∥CB,∴∠AFB=∠CBF,
∵BE平分∠ABC,∴∠ABE=∠CBE,∴∠AFB=∠ABF,∴AF=AB,又AG⊥BE,∴BG=FG.
∵AF=DF,AD=BC=6,∴AB=AF=3,
∵Rt△ABG中,
22.解析 (1)证明:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,∠FDC=∠B,∴DE=AF,
又∵AB=AC,∴∠B=∠C,∴∠FDC=∠C,∴DF=FC,∴DE+DF=AF+FC=AC.
(2)当点D在边BC的延长线上时,DE-DF=AC.
当点D在边BC的反向延长线上时,DF-DE=AC.
(3)当点D在边BC上时,DF=AC-DE=10-7=3.
当点D在边BC的反向延长线上时,DF=AC+DE=10+7=17.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
