人教版八年级数学上册 13.1.2线段的垂直平分线的性质 第1课时 教学设计
文档属性
| 名称 | 人教版八年级数学上册 13.1.2线段的垂直平分线的性质 第1课时 教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 170.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-17 00:00:00 | ||
图片预览

文档简介
13.1.2 线段的垂直平分线的性质
(第一课时)
一、教学内容分析
《线段的垂直平分线的性质》选自人教版《义务教育教科书 八年级上册》(2013版)第十三章《轴对称》13.1.2线段的垂直平分线的性质。在此之前,学生学习了全等三角形,对轴对称图形的性质有所认识,这为过渡到本节的学习起着铺垫作用。本节内容是今后证明线段相等和直线互相垂直的依据,因此本节课具有承上启下的重要作用。
二、学生学情分析
学生在此之前已经学习了轴对称图形,对线段的垂直平分线已经有了初步的认识,这为顺利完成本节课的教学任务打下了基础,但处于该阶段的学生语言表达能力较差,特别是几何语言的描述不规范,本节课几何语言理解表达问题较难,因此,教学中要加强推理证明步骤的规范化。
三、教学目标
1.知识与技能
(1)识记并理解线段垂直平分线的性质定理及其逆定理。
(2)掌握垂线的尺规作图方法并理解作法的依据及合理性。
2.过程与方法
使学生经历证明理解线段垂直平分线的性质定理及其逆定理的过程,熟悉证明的步骤。
3.情感态度与价值观
通过对定理的探究,培养学生自主学习勇于思考和探究的品质,让学生充分体会到探究的乐趣。
四、教学重难点
重点:线段的垂直平分线定理和逆定理的证明和运用。
难点:线段的垂直平分线定理和逆定理的证明和运用,线段的垂直平分线的画法。
五、教学过程设计
1.温故知新,导入新课
回顾线段的垂直平分线定义概念,探究线段的垂直平分线的性质。
提问:什么是垂直平分线?
垂直平分线具有哪些性质?
[设计意图]:帮助学生回顾上节课所学的线段的垂直平分线的定义,同时为本节课学习线段的垂直平分线的性质作铺垫。
(
A
B
l
P
1
P
2
P
3
)得出定义:经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线。
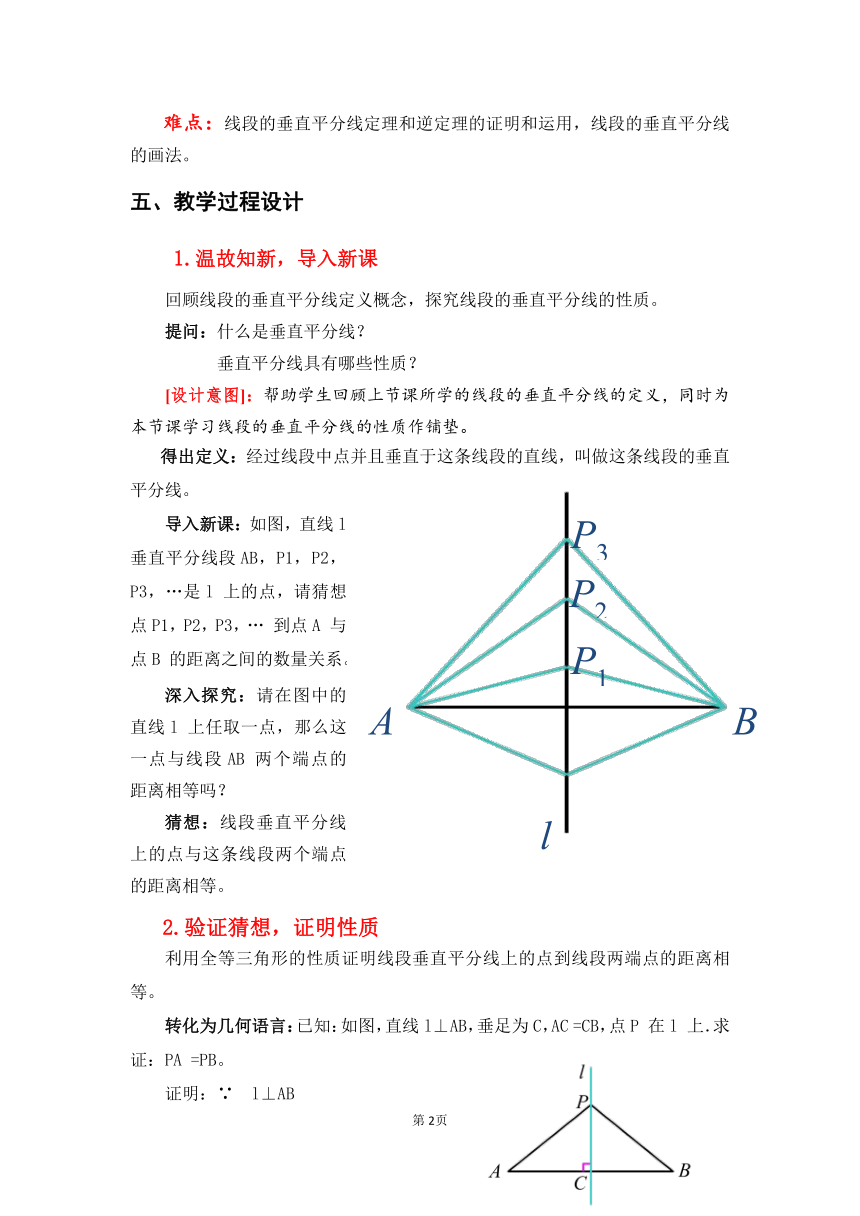
导入新课:如图,直线l 垂直平分线段AB,P1,P2,P3,…是l 上的点,请猜想点P1,P2,P3,… 到点A 与点B 的距离之间的数量关系。
深入探究:请在图中的直线l 上任取一点,那么这一点与线段AB 两个端点的距离相等吗?
猜想:线段垂直平分线上的点与这条线段两个端点的距离相等。
2.验证猜想,证明性质
利用全等三角形的性质证明线段垂直平分线上的点到线段两端点的距离相等。
转化为几何语言:已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.求证:PA =PB。
证明:∵ l⊥AB
∴ ∠PCA =∠PCB
又 AC =CB,PC =PC
∴ △PCA ≌△PCB(SAS)
∴ PA =PB。
[设计意图]:使学生经历证明理解线段垂直平分线的性质定理的过程,熟悉证明的步骤。
得出定义:线段垂直平分线上的点与这条线段两个端点的距离相等。用几何语言表示为:∵ CA =CB,l⊥AB,∴ PA =PB。
3.趁热打铁,巩固认知
1.如图,在△ABC 中,BC =8,AB 的中垂线 交BC于D,AC 的中垂线交BC 与E,则△ADE 的周长等 于___8___。
2.如图,AD⊥BC,BD =DC,点C 在AE 的垂直平分线上,AB,AC,CE 的长度有什么关系?AB+BD与DE 有什么关系?
解:∵ AD⊥BC,BD =DC
∴ AD 是BC 的垂直平分线
∴ AB =AC
∵ 点C 在AE 的垂直平分线上
∴ AC =CE. ∴ AB =AC =CE
∵ AB =CE,BD =DC,∴ AB +BD =CD +CE.
即 AB +BD =DE 。
[设计意图]:在巩固学生对线段的垂直平分线的性质的认知基础上,让学生学会应用该性质解答相关问题。
4.继续探究,判定证明
询问线段的垂直平分线的性质的逆定理是否成立?让学生参照刚刚证明定理的过程,自己证明线段垂直平分线的判定定理
提问:反过来,如果PA =PB,那么点P 是否在线段AB 的 垂直平分线上呢?
转化为几何语言:已知:如图,PA =PB.求证:PC⊥AB且AC=BC。
证明:如图作PC⊥AB
则∠PCA =∠PCB =90°
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC
∴ Rt△PCA ≌Rt△PCB(HL)
∴ AC =BC
又 PC⊥AB
∴ 点P 在线段AB 的垂直平分线上
课外思考:能否作AB的中线PC交AB于C,证明PC⊥AB
[设计意图]:通过对定理的探究,培养学生自主学习勇于思考和探究的品质,让学生充分体会到探究的乐趣。
得出定义:线段垂直平分线的判定:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。用几何符号表示为:∵ PA =PB,∴ 点P 在AB 的垂直平分线上。
练习3:如图,AB =AC,MB =MC.直线AM 是线段BC 的垂直平分线吗?
解:∵ AB =AC
∴ 点A 在BC 的垂直平分线。
∵ MB =MC
∵ 点M 在BC 的垂直平分线上
∴ 直线AM 是线段BC 的垂直平分线。
5.学以致用,尺规作图
教师在黑板上作图,教会学生如何用尺规作图的方法经过直线外一点作已知直线的垂线。
为什么任意取一点K ,使点K与点C 在直线两旁?
为什么要以大于的长为半径作弧?
(
E
) (
C
A
B
D
K
)为什么直线CF 就是所求作的垂线?
(
F
)[设计意图]:锻炼学生的动手操作能力,掌握垂线的尺规作图方法并理解作法的依据及合理性。
练习4:如图,过点P 画∠AOB 两边的垂线,并和同桌交流你的作图过程。
六、小结反思,整合强化
(1)线段垂直平分线的性质;
(2)线段垂直平分线的判定;
(3)对称图形对称轴的画法。
[设计意图]:引导学生从知识、技能、过程、方法、情感多方面进行反思总结,刷新单一的知识小结作法;养育学生反思总结习惯,提升学生数学学习元认知水平。
七、课后作业
1.必做题:P65页:第6、9题。2.课时练
[设计意图]:学以致用,巩固提高。
第5页
(第一课时)
一、教学内容分析
《线段的垂直平分线的性质》选自人教版《义务教育教科书 八年级上册》(2013版)第十三章《轴对称》13.1.2线段的垂直平分线的性质。在此之前,学生学习了全等三角形,对轴对称图形的性质有所认识,这为过渡到本节的学习起着铺垫作用。本节内容是今后证明线段相等和直线互相垂直的依据,因此本节课具有承上启下的重要作用。
二、学生学情分析
学生在此之前已经学习了轴对称图形,对线段的垂直平分线已经有了初步的认识,这为顺利完成本节课的教学任务打下了基础,但处于该阶段的学生语言表达能力较差,特别是几何语言的描述不规范,本节课几何语言理解表达问题较难,因此,教学中要加强推理证明步骤的规范化。
三、教学目标
1.知识与技能
(1)识记并理解线段垂直平分线的性质定理及其逆定理。
(2)掌握垂线的尺规作图方法并理解作法的依据及合理性。
2.过程与方法
使学生经历证明理解线段垂直平分线的性质定理及其逆定理的过程,熟悉证明的步骤。
3.情感态度与价值观
通过对定理的探究,培养学生自主学习勇于思考和探究的品质,让学生充分体会到探究的乐趣。
四、教学重难点
重点:线段的垂直平分线定理和逆定理的证明和运用。
难点:线段的垂直平分线定理和逆定理的证明和运用,线段的垂直平分线的画法。
五、教学过程设计
1.温故知新,导入新课
回顾线段的垂直平分线定义概念,探究线段的垂直平分线的性质。
提问:什么是垂直平分线?
垂直平分线具有哪些性质?
[设计意图]:帮助学生回顾上节课所学的线段的垂直平分线的定义,同时为本节课学习线段的垂直平分线的性质作铺垫。
(
A
B
l
P
1
P
2
P
3
)得出定义:经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线。
导入新课:如图,直线l 垂直平分线段AB,P1,P2,P3,…是l 上的点,请猜想点P1,P2,P3,… 到点A 与点B 的距离之间的数量关系。
深入探究:请在图中的直线l 上任取一点,那么这一点与线段AB 两个端点的距离相等吗?
猜想:线段垂直平分线上的点与这条线段两个端点的距离相等。
2.验证猜想,证明性质
利用全等三角形的性质证明线段垂直平分线上的点到线段两端点的距离相等。
转化为几何语言:已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.求证:PA =PB。
证明:∵ l⊥AB
∴ ∠PCA =∠PCB
又 AC =CB,PC =PC
∴ △PCA ≌△PCB(SAS)
∴ PA =PB。
[设计意图]:使学生经历证明理解线段垂直平分线的性质定理的过程,熟悉证明的步骤。
得出定义:线段垂直平分线上的点与这条线段两个端点的距离相等。用几何语言表示为:∵ CA =CB,l⊥AB,∴ PA =PB。
3.趁热打铁,巩固认知
1.如图,在△ABC 中,BC =8,AB 的中垂线 交BC于D,AC 的中垂线交BC 与E,则△ADE 的周长等 于___8___。
2.如图,AD⊥BC,BD =DC,点C 在AE 的垂直平分线上,AB,AC,CE 的长度有什么关系?AB+BD与DE 有什么关系?
解:∵ AD⊥BC,BD =DC
∴ AD 是BC 的垂直平分线
∴ AB =AC
∵ 点C 在AE 的垂直平分线上
∴ AC =CE. ∴ AB =AC =CE
∵ AB =CE,BD =DC,∴ AB +BD =CD +CE.
即 AB +BD =DE 。
[设计意图]:在巩固学生对线段的垂直平分线的性质的认知基础上,让学生学会应用该性质解答相关问题。
4.继续探究,判定证明
询问线段的垂直平分线的性质的逆定理是否成立?让学生参照刚刚证明定理的过程,自己证明线段垂直平分线的判定定理
提问:反过来,如果PA =PB,那么点P 是否在线段AB 的 垂直平分线上呢?
转化为几何语言:已知:如图,PA =PB.求证:PC⊥AB且AC=BC。
证明:如图作PC⊥AB
则∠PCA =∠PCB =90°
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC
∴ Rt△PCA ≌Rt△PCB(HL)
∴ AC =BC
又 PC⊥AB
∴ 点P 在线段AB 的垂直平分线上
课外思考:能否作AB的中线PC交AB于C,证明PC⊥AB
[设计意图]:通过对定理的探究,培养学生自主学习勇于思考和探究的品质,让学生充分体会到探究的乐趣。
得出定义:线段垂直平分线的判定:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。用几何符号表示为:∵ PA =PB,∴ 点P 在AB 的垂直平分线上。
练习3:如图,AB =AC,MB =MC.直线AM 是线段BC 的垂直平分线吗?
解:∵ AB =AC
∴ 点A 在BC 的垂直平分线。
∵ MB =MC
∵ 点M 在BC 的垂直平分线上
∴ 直线AM 是线段BC 的垂直平分线。
5.学以致用,尺规作图
教师在黑板上作图,教会学生如何用尺规作图的方法经过直线外一点作已知直线的垂线。
为什么任意取一点K ,使点K与点C 在直线两旁?
为什么要以大于的长为半径作弧?
(
E
) (
C
A
B
D
K
)为什么直线CF 就是所求作的垂线?
(
F
)[设计意图]:锻炼学生的动手操作能力,掌握垂线的尺规作图方法并理解作法的依据及合理性。
练习4:如图,过点P 画∠AOB 两边的垂线,并和同桌交流你的作图过程。
六、小结反思,整合强化
(1)线段垂直平分线的性质;
(2)线段垂直平分线的判定;
(3)对称图形对称轴的画法。
[设计意图]:引导学生从知识、技能、过程、方法、情感多方面进行反思总结,刷新单一的知识小结作法;养育学生反思总结习惯,提升学生数学学习元认知水平。
七、课后作业
1.必做题:P65页:第6、9题。2.课时练
[设计意图]:学以致用,巩固提高。
第5页
