九年级数学上册22.3实际问题与二次函数 同步训练(word、含解析)
文档属性
| 名称 | 九年级数学上册22.3实际问题与二次函数 同步训练(word、含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 579.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-17 13:03:36 | ||
图片预览


文档简介
22.3《实际问题与二次函数》同步训练
一、单选题
1.在体育选项报考前,某九年级学生对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系为y=,由此可知该生此次实心球训练的成绩为( )
A.6米 B.10米 C.12米 D.15米
2.从地面竖直向上抛出一小球,小球的高度米与小球运动的时间秒之间的关系式为若小球在第秒与第秒时的高度相同,则在下列时间中小球所在高度最高的是( )
A.第秒 B.第秒 C.第秒 D.第秒
3.某商场降价销售一批名牌衬衫,已知所获得利润(元)与降价金额(元)之间的关系是,则获利最多为()
A.元 B.元 C.元 D.元
4.竖直向上发射的小球的高度关于运动时间的函数表达式为,其图象如图所示,若小球发射后第2秒与第6秒时的高度相等,则下列时刻中小球的高度最高的是( )
A.第3秒 B.第3.5秒 C.第4秒 D.第6秒
5.在地球上同一地点,不同质量的物体从同一高度同时下落,如果除地球引力外不考虑其他外力的作用,那么它们的落地时间相同.物体的下落距离h(m)与下落时间t(s)之间的函数表达式为h=gt2.其中g取值为9.8m/s2.小莉进行自由落体实验,她从某建筑物抛下一个小球,经过4s后落地,则该建筑物的高度约为( )
A.98m B.78.4m C.49m D.36.2m
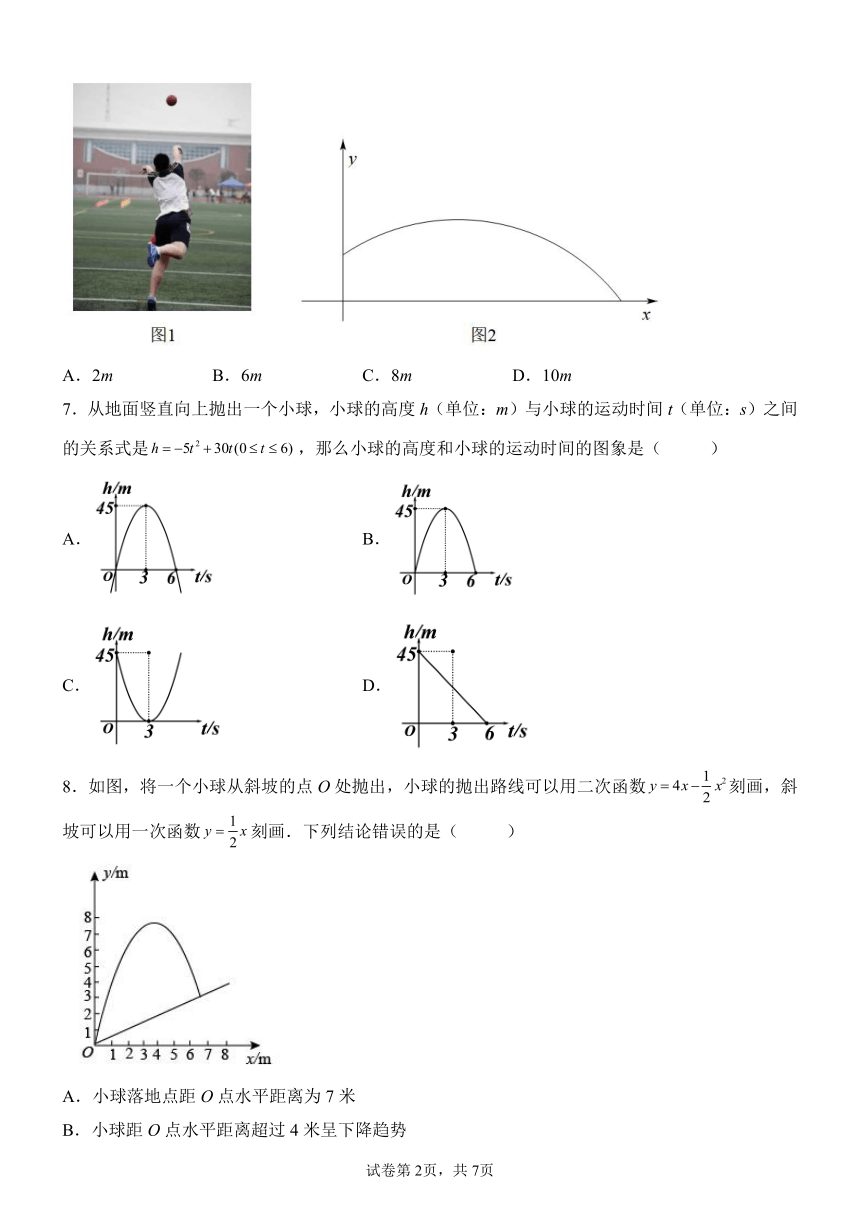
6.如图1,校运动会上,初一的同学们进行了投实心球比赛.我们发现,实心球在空中飞行的轨迹可以近似看作是抛物线.如图2建立平面直角坐标系,已知实心球运动的高度y(m)与水平距离x(m)之间的函数关系是y=,则该同学此次投掷实心球的成绩是( )
A.2m B.6m C.8m D.10m
7.从地面竖直向上抛出一个小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是,那么小球的高度和小球的运动时间的图象是( )
A. B.
C. D.
8.如图,将一个小球从斜坡的点O处抛出,小球的抛出路线可以用二次函数刻画,斜坡可以用一次函数刻画.下列结论错误的是( )
A.小球落地点距O点水平距离为7米
B.小球距O点水平距离超过4米呈下降趋势
C.当小球抛出高度达到7.5m时,小球距O点水平距离为3m
D.小球距斜坡的最大铅直高度为
9.如图,正方形ABCD的边长为2cm,点P,点Q同时从点A出发,速度均为2cm/s,点P沿A-D-C向点C运动,点Q沿A-B-C向点C运动,则△APQ的面积S(cm2)与运动时间t(s)之间函数关系的大致图象是( )
A.B.C. D.
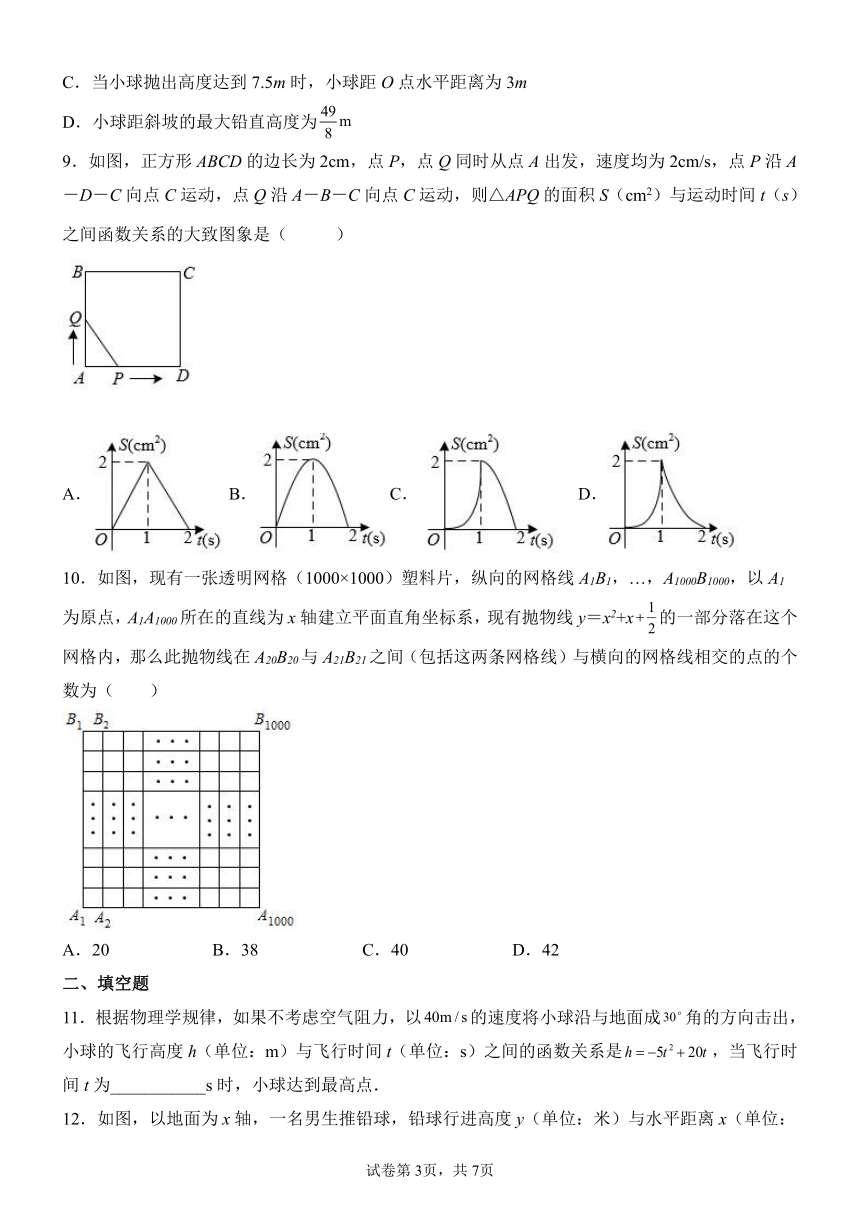
10.如图,现有一张透明网格(1000×1000)塑料片,纵向的网格线A1B1,…,A1000B1000,以A1为原点,A1A1000所在的直线为x轴建立平面直角坐标系,现有抛物线y=x2+x的一部分落在这个网格内,那么此抛物线在A20B20与A21B21之间(包括这两条网格线)与横向的网格线相交的点的个数为( )
A.20 B.38 C.40 D.42
二、填空题
11.根据物理学规律,如果不考虑空气阻力,以的速度将小球沿与地面成角的方向击出,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的函数关系是,当飞行时间t为___________s时,小球达到最高点.
12.如图,以地面为x轴,一名男生推铅球,铅球行进高度y(单位:米)与水平距离x(单位:米)之间的关系是.则他将铅球推出的距离是___米.
13.据了解,某蔬菜种植基地2019年的蔬菜产量为100万吨,2021年的蔬菜产量为万吨,如果2019年至2021年蔬菜产量的年平均增长率为,那么关于的函数解析式为_________.
14.如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,以B为原点、AB所在水平线为x轴建立坐标系,拱桥对应抛物线的解析式为______.
15.某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为______________元(利润=总销售额-总成本).
16.如图,水池中心点O处竖直安装一水管,水管喷头喷出抛物线形水柱,喷头上下移动时,抛物线形水柱随之竖直上下平移,水柱落点与点O在同一水平面.安装师傅调试发现,喷头高时,水柱落点距O点;喷头高时,水柱落点距O点.那么喷头高_______________m时,水柱落点距O点.
三、解答题
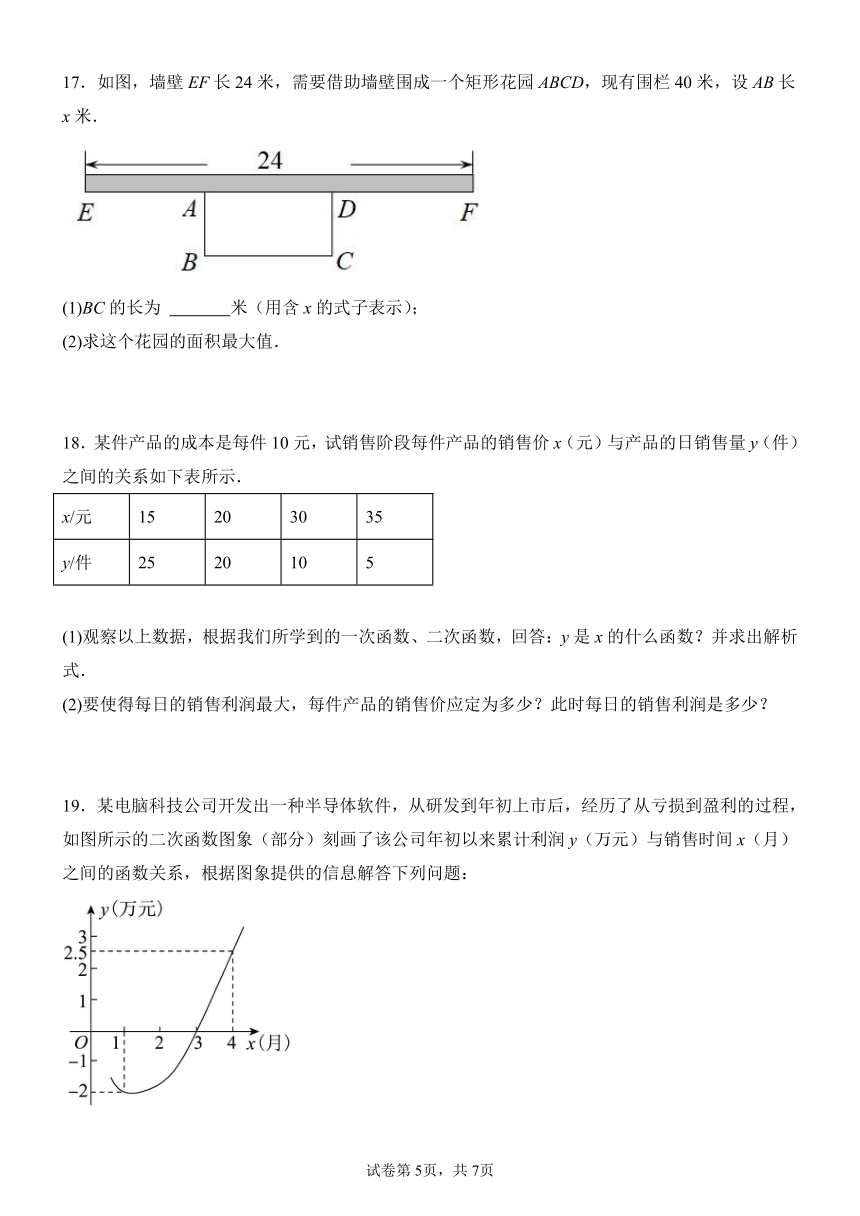
17.如图,墙壁EF长24米,需要借助墙壁围成一个矩形花园ABCD,现有围栏40米,设AB长x米.
(1)BC的长为 米(用含x的式子表示);
(2)求这个花园的面积最大值.
18.某件产品的成本是每件10元,试销售阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表所示.
x/元 15 20 30 35
y/件 25 20 10 5
(1)观察以上数据,根据我们所学到的一次函数、二次函数,回答:y是x的什么函数?并求出解析式.
(2)要使得每日的销售利润最大,每件产品的销售价应定为多少?此时每日的销售利润是多少?
19.某电脑科技公司开发出一种半导体软件,从研发到年初上市后,经历了从亏损到盈利的过程,如图所示的二次函数图象(部分)刻画了该公司年初以来累计利润y(万元)与销售时间x(月)之间的函数关系,根据图象提供的信息解答下列问题:
(1)求y与x之间的函数表达式;
(2)截止到几月末公司累计利润达到30万元?
20.某运动品牌销售商发现某种运动鞋市场需求量较大,经过市场调查发现月销售量y(双)与销售单价x(元)之间的函数关系为,而该种运动鞋的进价z(元)与销售单价x(元)之间的函数关系为,已知销售商每月支付员工工资和场地租金等费用总计20000元(注:月获利=月销售总额-月进货总价-工资和租金费用)
(1)求月获利W(元)与x之间的函数关系式;
(2)当销售单价x为何值时,月获利最大,最大值为多少?
(3)若该销售商销售这种品牌运动鞋的月获利不低于2.2万元,请确定销售单价的范围,在此情况下,要使销售量最大,你认为销售单价应定为多少元?
21.某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现:若每箱以50元的价格出售,平均每天销售80箱,价格每提高1元,平均每天少销售2箱.
(1)求平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式;
(2)求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式;
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
22.随着地铁和共享电动车的发展,“地铁+电动车”已成为很多市民出行的选择,小丽从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享电动车车回家,设她出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间(单位:分钟)是关于x的一次函数,其关系如下表:
地铁站 A B C D E
x(千米) 8 10 11.8 13 15
(分钟) 10 11 11.9 12.5 13.5
(1)求关于x的函数表达式.
(2)小丽骑电动车的时间(单位:分钟)也受x的影响,其关系可以用来描述,请问:小丽应选择在那一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
铅球落地时高度为0,即当y=0时,
=0,
解得x1=10,x2=-2(舍去),
所以该生此次实心球训练的成绩为10米,
故选:B.
2.B
解:由题意可得,
当时,取得最大值,
当时,取得最大值,
故选:B.
3.D
解:对于抛物线,
,
时,有最大值,最大值为,
故选:D.
4.C
解:由题意可知:小球发射后第2秒与第6秒时的高度相等,
即4a+2b=36a+6b,
解得b=﹣8a,
函数h=at2+bt的对称轴t=﹣=4,
故在t=4s时,小球的高度最高,
故选:C.
5.B
解:把t=4代入h=gt2得,
故选:B.
6.D
解:该同学此次投掷实心球的成绩就是实心球落地时的水平距离,
∴令y=0,则=0,
整理得:x2-8x-20=0,
解得:x1=10,x2=-2(舍去),
∴该同学此次投掷实心球的成绩为10m,
故选:D.
7.B
解:,
令h=0,,
解得:t=0或6,
∴小球的高度和小球的运动时间的图象是开口向下,位于x轴上方抛物线的一段,且顶点坐标为(3,45),
∴B选项图象符合题意.
故选:B
8.C
解:联立两函数解析式,得
,解得:或,
则小球落地点距O点水平距离为7米,
故A选项不符合题意;
∵,
则抛物线的对称轴为x=4,
∵<0,
∴当x>4时,y随x的增大而减小,
即小球距O点水平距离超过4米呈下降趋势,
故B选项不符合题意;
当y=7.5时,7.5=4x-x2,
整理得x2-8x+15=0,
解得,x1=3,x2=5,
∴当小球抛出高度达到7.5m时,小球水平距O点水平距离为3m或5m,故此选项符合题意;
如图,设抛物线上一点A(x, 4x-x2),过点A作AB⊥x轴于C,交直线y=x于B,
∴B(x,),
∴AB=4x-x2-=-x2x=-(x-)2+,
∵<0,
∴当x=时,AB有最大值,最大值=,
即小球距斜坡的最大铅直高度为,
故D选项不符合题意.
故选:C.
9.C
当Q、P两点分别在AB、AD上时,即
可知AQ=t,AP=t,
△AQP的面积为:,;
当Q、P两点分别在BC、DC上时,
连接AC,如图,
根据题意有:AB+BQ=t,则QC=AB+BC-(AB+BQ),
∵正方形ABCD的边长为2,
∴AB=BC=CD=AD=2,
∴QC=4-t,
同理可得PC=4-t,
∵△APQ的面积为四边形AQCP的面积减去△CQP面积,
又∵四边形AQCP的面积等于△AQC与△APC的面积之和,
∴,
∵、、,
∴,整理得:,
∴,,
则有,
据此可知选C,
故选:C.
10.C
∵A1为原点,
∴A20对应的x=19,A21对应的x=20,
当x=19时,y1380,
当x=20时,y2,
∴y2﹣y1=40,
∴此抛物线在A20B20与A21B21之间与横向的网格线相交的点的个数为40个,
故选:C.
11.2
根据题意,有,
当时,有最大值.
故答案为:2.
12.10
解:当y=0时,,
解得:x1=10,x2=-2(不合题意,舍去),
所以推铅球的距离是10米;
故答案为:10.
13.
解:根据题意可得:2020年的蔬菜产量为,
2021年的蔬菜产量为,
∴,
故答案为: .
14.(或)
解:以B为原点、AB所在水平线为x轴建立坐标系,
由题意得A(-4,0),顶点(-2,2),
设抛物线的解析式为:
把A(-4,0)代入,得
4a=﹣2,解得a,
所以抛物线解析式为.
故答案为:.
15.121
解:当时,设,把(10,20),(20,10)代入可得:
,
解得,
∴每天的销售量y(个)与销售价格x(元/个)的函数解析式为,
设该食品零售店每天销售这款冷饮产品的利润为w元,
,
∵1<0,
∴当时,w有最大值为121,
故答案为:121.
16.8
解:由题意可知,在调整喷头高度的过程中,水柱的形状不发生变化,
当喷头高2.5m时,可设y=ax2+bx+2.5,
将(2.5,0)代入解析式得出2.5a+b+1=0①,
喷头高4m时,可设y=ax2+bx+4,
将(3,0)代入解析式得9a+3b+4=0②,
联立可求出,,
设喷头高为h时,水柱落点距O点4m,
∴此时的解析式为,
将(4,0)代入可得,
解得h=8.
故答案为:8.
17
(1)
解:由题意知AB+BC+CD=40米,AB=CD=x米,
所以BC的长为(40-2x)米,
故答案为:(40-2x);
(2)
解:设这个花园的面积为y 平方米,由题意得:
y=x(40-2x)
=-2x2+40x
=-2(x-10)2+200,
∵-2<0,
∴当x=10时,y取得最大值,最大值为200,
答:这个花园的面积最大值为200平方米.
18.
(1)解:由表中数据可知,y是x的一次函数. 设此一次函数关系式为,则,解得,,故一次函数的关系式为;
(2)解:设所获利润为W元,则,所以产品的销售价应定为25元,此时每日的销售利润最大,为225元.
19
(1)
解:设y=a(x-1)2-2,
把(4,2.5)代入得:
2.5=a(4-1)2-2,
解得a=,
∴函数表达式为:;
(2)
由题意得:,
解得:x1=9,x2=-7(舍),
∴截止到9月末公司累计利润达到30万元.
20.
(1)
解:根据题意得∶;
(2)
解:,
∵,
∴当销售单价为550元时,月获利最大,最大值为30000元;
(3)
解:当月获利为2.2万元时,即,解得,.
画出W关于x的函数图象的草图,如图,
利用图象可知要使月获利不低于2.2万元,销售单价应在450元到650元之间.
∵销售单价越低,销售量越大,又要使月获利不低于2.2万元,
∴销售单价应定为450元.
21
(1)
解:由题意得:y=80﹣2(x﹣50)
化简得:y=﹣2x+180;
(2)
解:由题意得:w=(x﹣40)y
=(x﹣40)(﹣2x+180)
=﹣2x2+260x﹣7200;
(3)
解:w=﹣2x2+260x﹣7200=-2(x-65)2+1250
∵a=﹣2<0,
∴抛物线开口向下.当x=65时,w有最大值.
又∵x<65,w随x的增大而增大.
∵40∴当x=55元时,w的最大值为1050元.
∴当每箱苹果的销售价为55元时,可以获得1050元的最大利润.
22
(1)
解:(1)设,将(8,10),(10,11)代入得:
,解得,
∴
(2)
解:设小丽从文化宫回到家所需的时间为y,则:
则当x=10时,y1+y2取最小值,
则应在B站出地铁,时间最短,为29min.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.在体育选项报考前,某九年级学生对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系为y=,由此可知该生此次实心球训练的成绩为( )
A.6米 B.10米 C.12米 D.15米
2.从地面竖直向上抛出一小球,小球的高度米与小球运动的时间秒之间的关系式为若小球在第秒与第秒时的高度相同,则在下列时间中小球所在高度最高的是( )
A.第秒 B.第秒 C.第秒 D.第秒
3.某商场降价销售一批名牌衬衫,已知所获得利润(元)与降价金额(元)之间的关系是,则获利最多为()
A.元 B.元 C.元 D.元
4.竖直向上发射的小球的高度关于运动时间的函数表达式为,其图象如图所示,若小球发射后第2秒与第6秒时的高度相等,则下列时刻中小球的高度最高的是( )
A.第3秒 B.第3.5秒 C.第4秒 D.第6秒
5.在地球上同一地点,不同质量的物体从同一高度同时下落,如果除地球引力外不考虑其他外力的作用,那么它们的落地时间相同.物体的下落距离h(m)与下落时间t(s)之间的函数表达式为h=gt2.其中g取值为9.8m/s2.小莉进行自由落体实验,她从某建筑物抛下一个小球,经过4s后落地,则该建筑物的高度约为( )
A.98m B.78.4m C.49m D.36.2m
6.如图1,校运动会上,初一的同学们进行了投实心球比赛.我们发现,实心球在空中飞行的轨迹可以近似看作是抛物线.如图2建立平面直角坐标系,已知实心球运动的高度y(m)与水平距离x(m)之间的函数关系是y=,则该同学此次投掷实心球的成绩是( )
A.2m B.6m C.8m D.10m
7.从地面竖直向上抛出一个小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是,那么小球的高度和小球的运动时间的图象是( )
A. B.
C. D.
8.如图,将一个小球从斜坡的点O处抛出,小球的抛出路线可以用二次函数刻画,斜坡可以用一次函数刻画.下列结论错误的是( )
A.小球落地点距O点水平距离为7米
B.小球距O点水平距离超过4米呈下降趋势
C.当小球抛出高度达到7.5m时,小球距O点水平距离为3m
D.小球距斜坡的最大铅直高度为
9.如图,正方形ABCD的边长为2cm,点P,点Q同时从点A出发,速度均为2cm/s,点P沿A-D-C向点C运动,点Q沿A-B-C向点C运动,则△APQ的面积S(cm2)与运动时间t(s)之间函数关系的大致图象是( )
A.B.C. D.
10.如图,现有一张透明网格(1000×1000)塑料片,纵向的网格线A1B1,…,A1000B1000,以A1为原点,A1A1000所在的直线为x轴建立平面直角坐标系,现有抛物线y=x2+x的一部分落在这个网格内,那么此抛物线在A20B20与A21B21之间(包括这两条网格线)与横向的网格线相交的点的个数为( )
A.20 B.38 C.40 D.42
二、填空题
11.根据物理学规律,如果不考虑空气阻力,以的速度将小球沿与地面成角的方向击出,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的函数关系是,当飞行时间t为___________s时,小球达到最高点.
12.如图,以地面为x轴,一名男生推铅球,铅球行进高度y(单位:米)与水平距离x(单位:米)之间的关系是.则他将铅球推出的距离是___米.
13.据了解,某蔬菜种植基地2019年的蔬菜产量为100万吨,2021年的蔬菜产量为万吨,如果2019年至2021年蔬菜产量的年平均增长率为,那么关于的函数解析式为_________.
14.如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,以B为原点、AB所在水平线为x轴建立坐标系,拱桥对应抛物线的解析式为______.
15.某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为______________元(利润=总销售额-总成本).
16.如图,水池中心点O处竖直安装一水管,水管喷头喷出抛物线形水柱,喷头上下移动时,抛物线形水柱随之竖直上下平移,水柱落点与点O在同一水平面.安装师傅调试发现,喷头高时,水柱落点距O点;喷头高时,水柱落点距O点.那么喷头高_______________m时,水柱落点距O点.
三、解答题
17.如图,墙壁EF长24米,需要借助墙壁围成一个矩形花园ABCD,现有围栏40米,设AB长x米.
(1)BC的长为 米(用含x的式子表示);
(2)求这个花园的面积最大值.
18.某件产品的成本是每件10元,试销售阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表所示.
x/元 15 20 30 35
y/件 25 20 10 5
(1)观察以上数据,根据我们所学到的一次函数、二次函数,回答:y是x的什么函数?并求出解析式.
(2)要使得每日的销售利润最大,每件产品的销售价应定为多少?此时每日的销售利润是多少?
19.某电脑科技公司开发出一种半导体软件,从研发到年初上市后,经历了从亏损到盈利的过程,如图所示的二次函数图象(部分)刻画了该公司年初以来累计利润y(万元)与销售时间x(月)之间的函数关系,根据图象提供的信息解答下列问题:
(1)求y与x之间的函数表达式;
(2)截止到几月末公司累计利润达到30万元?
20.某运动品牌销售商发现某种运动鞋市场需求量较大,经过市场调查发现月销售量y(双)与销售单价x(元)之间的函数关系为,而该种运动鞋的进价z(元)与销售单价x(元)之间的函数关系为,已知销售商每月支付员工工资和场地租金等费用总计20000元(注:月获利=月销售总额-月进货总价-工资和租金费用)
(1)求月获利W(元)与x之间的函数关系式;
(2)当销售单价x为何值时,月获利最大,最大值为多少?
(3)若该销售商销售这种品牌运动鞋的月获利不低于2.2万元,请确定销售单价的范围,在此情况下,要使销售量最大,你认为销售单价应定为多少元?
21.某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现:若每箱以50元的价格出售,平均每天销售80箱,价格每提高1元,平均每天少销售2箱.
(1)求平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式;
(2)求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式;
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
22.随着地铁和共享电动车的发展,“地铁+电动车”已成为很多市民出行的选择,小丽从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享电动车车回家,设她出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间(单位:分钟)是关于x的一次函数,其关系如下表:
地铁站 A B C D E
x(千米) 8 10 11.8 13 15
(分钟) 10 11 11.9 12.5 13.5
(1)求关于x的函数表达式.
(2)小丽骑电动车的时间(单位:分钟)也受x的影响,其关系可以用来描述,请问:小丽应选择在那一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
铅球落地时高度为0,即当y=0时,
=0,
解得x1=10,x2=-2(舍去),
所以该生此次实心球训练的成绩为10米,
故选:B.
2.B
解:由题意可得,
当时,取得最大值,
当时,取得最大值,
故选:B.
3.D
解:对于抛物线,
,
时,有最大值,最大值为,
故选:D.
4.C
解:由题意可知:小球发射后第2秒与第6秒时的高度相等,
即4a+2b=36a+6b,
解得b=﹣8a,
函数h=at2+bt的对称轴t=﹣=4,
故在t=4s时,小球的高度最高,
故选:C.
5.B
解:把t=4代入h=gt2得,
故选:B.
6.D
解:该同学此次投掷实心球的成绩就是实心球落地时的水平距离,
∴令y=0,则=0,
整理得:x2-8x-20=0,
解得:x1=10,x2=-2(舍去),
∴该同学此次投掷实心球的成绩为10m,
故选:D.
7.B
解:,
令h=0,,
解得:t=0或6,
∴小球的高度和小球的运动时间的图象是开口向下,位于x轴上方抛物线的一段,且顶点坐标为(3,45),
∴B选项图象符合题意.
故选:B
8.C
解:联立两函数解析式,得
,解得:或,
则小球落地点距O点水平距离为7米,
故A选项不符合题意;
∵,
则抛物线的对称轴为x=4,
∵<0,
∴当x>4时,y随x的增大而减小,
即小球距O点水平距离超过4米呈下降趋势,
故B选项不符合题意;
当y=7.5时,7.5=4x-x2,
整理得x2-8x+15=0,
解得,x1=3,x2=5,
∴当小球抛出高度达到7.5m时,小球水平距O点水平距离为3m或5m,故此选项符合题意;
如图,设抛物线上一点A(x, 4x-x2),过点A作AB⊥x轴于C,交直线y=x于B,
∴B(x,),
∴AB=4x-x2-=-x2x=-(x-)2+,
∵<0,
∴当x=时,AB有最大值,最大值=,
即小球距斜坡的最大铅直高度为,
故D选项不符合题意.
故选:C.
9.C
当Q、P两点分别在AB、AD上时,即
可知AQ=t,AP=t,
△AQP的面积为:,;
当Q、P两点分别在BC、DC上时,
连接AC,如图,
根据题意有:AB+BQ=t,则QC=AB+BC-(AB+BQ),
∵正方形ABCD的边长为2,
∴AB=BC=CD=AD=2,
∴QC=4-t,
同理可得PC=4-t,
∵△APQ的面积为四边形AQCP的面积减去△CQP面积,
又∵四边形AQCP的面积等于△AQC与△APC的面积之和,
∴,
∵、、,
∴,整理得:,
∴,,
则有,
据此可知选C,
故选:C.
10.C
∵A1为原点,
∴A20对应的x=19,A21对应的x=20,
当x=19时,y1380,
当x=20时,y2,
∴y2﹣y1=40,
∴此抛物线在A20B20与A21B21之间与横向的网格线相交的点的个数为40个,
故选:C.
11.2
根据题意,有,
当时,有最大值.
故答案为:2.
12.10
解:当y=0时,,
解得:x1=10,x2=-2(不合题意,舍去),
所以推铅球的距离是10米;
故答案为:10.
13.
解:根据题意可得:2020年的蔬菜产量为,
2021年的蔬菜产量为,
∴,
故答案为: .
14.(或)
解:以B为原点、AB所在水平线为x轴建立坐标系,
由题意得A(-4,0),顶点(-2,2),
设抛物线的解析式为:
把A(-4,0)代入,得
4a=﹣2,解得a,
所以抛物线解析式为.
故答案为:.
15.121
解:当时,设,把(10,20),(20,10)代入可得:
,
解得,
∴每天的销售量y(个)与销售价格x(元/个)的函数解析式为,
设该食品零售店每天销售这款冷饮产品的利润为w元,
,
∵1<0,
∴当时,w有最大值为121,
故答案为:121.
16.8
解:由题意可知,在调整喷头高度的过程中,水柱的形状不发生变化,
当喷头高2.5m时,可设y=ax2+bx+2.5,
将(2.5,0)代入解析式得出2.5a+b+1=0①,
喷头高4m时,可设y=ax2+bx+4,
将(3,0)代入解析式得9a+3b+4=0②,
联立可求出,,
设喷头高为h时,水柱落点距O点4m,
∴此时的解析式为,
将(4,0)代入可得,
解得h=8.
故答案为:8.
17
(1)
解:由题意知AB+BC+CD=40米,AB=CD=x米,
所以BC的长为(40-2x)米,
故答案为:(40-2x);
(2)
解:设这个花园的面积为y 平方米,由题意得:
y=x(40-2x)
=-2x2+40x
=-2(x-10)2+200,
∵-2<0,
∴当x=10时,y取得最大值,最大值为200,
答:这个花园的面积最大值为200平方米.
18.
(1)解:由表中数据可知,y是x的一次函数. 设此一次函数关系式为,则,解得,,故一次函数的关系式为;
(2)解:设所获利润为W元,则,所以产品的销售价应定为25元,此时每日的销售利润最大,为225元.
19
(1)
解:设y=a(x-1)2-2,
把(4,2.5)代入得:
2.5=a(4-1)2-2,
解得a=,
∴函数表达式为:;
(2)
由题意得:,
解得:x1=9,x2=-7(舍),
∴截止到9月末公司累计利润达到30万元.
20.
(1)
解:根据题意得∶;
(2)
解:,
∵,
∴当销售单价为550元时,月获利最大,最大值为30000元;
(3)
解:当月获利为2.2万元时,即,解得,.
画出W关于x的函数图象的草图,如图,
利用图象可知要使月获利不低于2.2万元,销售单价应在450元到650元之间.
∵销售单价越低,销售量越大,又要使月获利不低于2.2万元,
∴销售单价应定为450元.
21
(1)
解:由题意得:y=80﹣2(x﹣50)
化简得:y=﹣2x+180;
(2)
解:由题意得:w=(x﹣40)y
=(x﹣40)(﹣2x+180)
=﹣2x2+260x﹣7200;
(3)
解:w=﹣2x2+260x﹣7200=-2(x-65)2+1250
∵a=﹣2<0,
∴抛物线开口向下.当x=65时,w有最大值.
又∵x<65,w随x的增大而增大.
∵40
∴当每箱苹果的销售价为55元时,可以获得1050元的最大利润.
22
(1)
解:(1)设,将(8,10),(10,11)代入得:
,解得,
∴
(2)
解:设小丽从文化宫回到家所需的时间为y,则:
则当x=10时,y1+y2取最小值,
则应在B站出地铁,时间最短,为29min.
答案第1页,共2页
答案第1页,共2页
同课章节目录
