北师大版(2019)必修第一册第七章 概率 培优专练(Word版含答案)
文档属性
| 名称 | 北师大版(2019)必修第一册第七章 概率 培优专练(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 212.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-15 05:39:49 | ||
图片预览



文档简介
《第七章 概率》培优专练
一、选择题
1.现有如表所示的五项运动供选择,记试验F“某人运动的总时长大于或等于60 min的运动组合方式”,则该试验中样本点的个数为( )
A运动 B运动 C运动 D运动 E运动
7:00~8:00 8:00~9:00 9:00~10:00 10:00~11:00 11:00~12:00
30 min 20 min 40 min 30 min 30 min
A.7 B.6 C.10 D.23
2.《易·系辞上》有“河出图,洛出书”之说,河图、洛书是中华文化、阴阳五行术数之源,其中河图的排列结构是一、六在后,二、七在前,三、八在左,四、九在右,五、十背中,如图,白圈为阳数,黑点为阴数,若从阴数和阳数中各取一数,则其差的绝对值为5的概率为( )
A. B. C. D.
3.我国古代数学著作《周髀算经》中有这样的表述:“若求邪至日者,以日下为勾,日高为股.勾股各自乘,并而开方除之,得邪至日.”这就是我们熟知的勾股定理.勾股数组是指满足a2+b2=c2的正整数组(a,b,c).现将一枚质地均匀的骰子抛掷三次,则三次向上的点数恰好组成勾股数组的概率是( )
A. B. C. D.
4.法国有个名人叫作布莱士·帕斯卡,他认识一个赌徒,这个赌徒向他提出一个问题:甲、乙两个人赌博,在他们下赌金之后,约定谁先赢满5局,谁就获得全部赌金700法郎,赌了半天,甲赢了4局,乙赢了3局,时间很晚了,他们都不想再赌下去,但是不知道赌金如何分配才合理.假设每局甲、乙两人获胜的概率均为,且每局输赢相互独立,那么这700法郎比较合理的分配方法是( )
A.甲400法郎,乙300法郎
B.甲500法郎,乙200法郎
C.甲525法郎,乙175法郎
D.甲350法郎,乙350法郎
5.数学上有种水仙花数,它是指各位数字的立方和等于其本身的三位数.水仙花数共有4个,其中仅有1个在区间(150,160)内,我们姑且称它为“水仙四妹”,则从集合{147,152,154,157,“水仙四妹”}的5个元素中任意取3个整数,则这3个整数中含有“水仙四妹”,且其余两个整数至少有一个比“水仙四妹”小的概率是( )
A. B. C. D.
6.一个三位自然数,百位、十位、个位上的数字依次为a,b,c,当且仅当a>b,bA. B.
C. D.
二、非选择题
7.用数字1,2组成一个四位数,则数字1,2都出现的概率为 .
8.从正六边形的6个顶点中随机选出4个,以它们作为顶点的四边形是矩形的概率为 .
9.古代“五行”学说认为“物质分金、木、水、火、土五种属性,金克木,木克土,土克水,水克火,火克金”,从五种不同属性的物质中随机抽取两种,则抽取的两种物质不相克的概率为 .
10.算盘是中国传统的计算工具.下图是一把算盘的初始状态,自右向左,分别是个位、十位、百位……,上面1粒珠(简称上珠)代表5,下面1粒珠(简称下珠)代表1,即5粒下珠的大小等于同组1粒上珠的大小.现从个位、十位、百位和千位这四组中随机拨动2粒珠(约定每档的上珠中最上面的1粒和下珠中最下面的1粒不使用,上珠只能往下拨,下珠只能往上拨),则算盘表示的整数能够被5整除的概率为 .
11.[2022黑龙江哈六中高二上期中考试]某商场做促销活动,顾客每购满100元可抽奖一次.在一个口袋内装有除颜色外其余完全相同的5个小球,其中3个红球、1个黑球、1个黄球.某顾客购满100元,可抽奖一次.
(1)若从中依次不放回地取出2个球,取出的球中有黄球,则送一件价值10元的礼品,求这位顾客能获得一件价值10元的礼品的概率;
(2)若从口袋中连续取两次球,每次取1个球后放回,当取出的2个球中没有红球时,送一件价值50元的礼品,问这位顾客获得一件价值50元的礼品的可能性会超过20%吗
12.为了让建筑类学生了解古建筑设计与构造的原理,某建筑大学为大三和大四的学生开设了一门选修课程《营造法式及其注释》.为检测学生学习效果,要求所有选修该门课程的学生完成“应用营造法式独立制作一件古建筑模型”的作业.已知选修该门课程的大三与大四学生的人数之比为3∶2,现用分层随机抽样的方法从所有作业中随机抽取100份(每位学生均上交一份作业),并评出成绩,得到如下频数分布表.
成绩/分 [50,60) [60,70) [70,80) [80,90) [90,100]
频数(不分年级) 4 x 20 38 30
频数(大三年级) 3 6 15 y 12
(1)求x,y的值,若以频率作为概率,从选修该门课程的大四学生中随机选取1名,试估计该学生的作业成绩在[60,80)的概率;
(2)估计这100份作业中大三学生作业的平均成绩(同一组中的数据用该组区间的中点值为代表).
13.随着经济全球化、信息化,企业之间的竞争从资源的争夺转向人才的竞争.吸引、留住、培养和用好人才成为人力资源管理的战略目标和紧迫任务.在此背景下,某信息网站在15个城市对刚毕业的大学生的月平均工资和月平均期望工资进行了调查,数据如图所示.
(1)若某大学毕业生从这15个城市中随机选择 1个城市就业,求该生选中月平均工资高于 8 500元的城市的概率;
(2)若从月平均期望工资与月平均工资之差的绝对值高于1 000元的城市中随机选择2个城市,求这2个城市的月平均期望工资都低于 8 500元的概率.
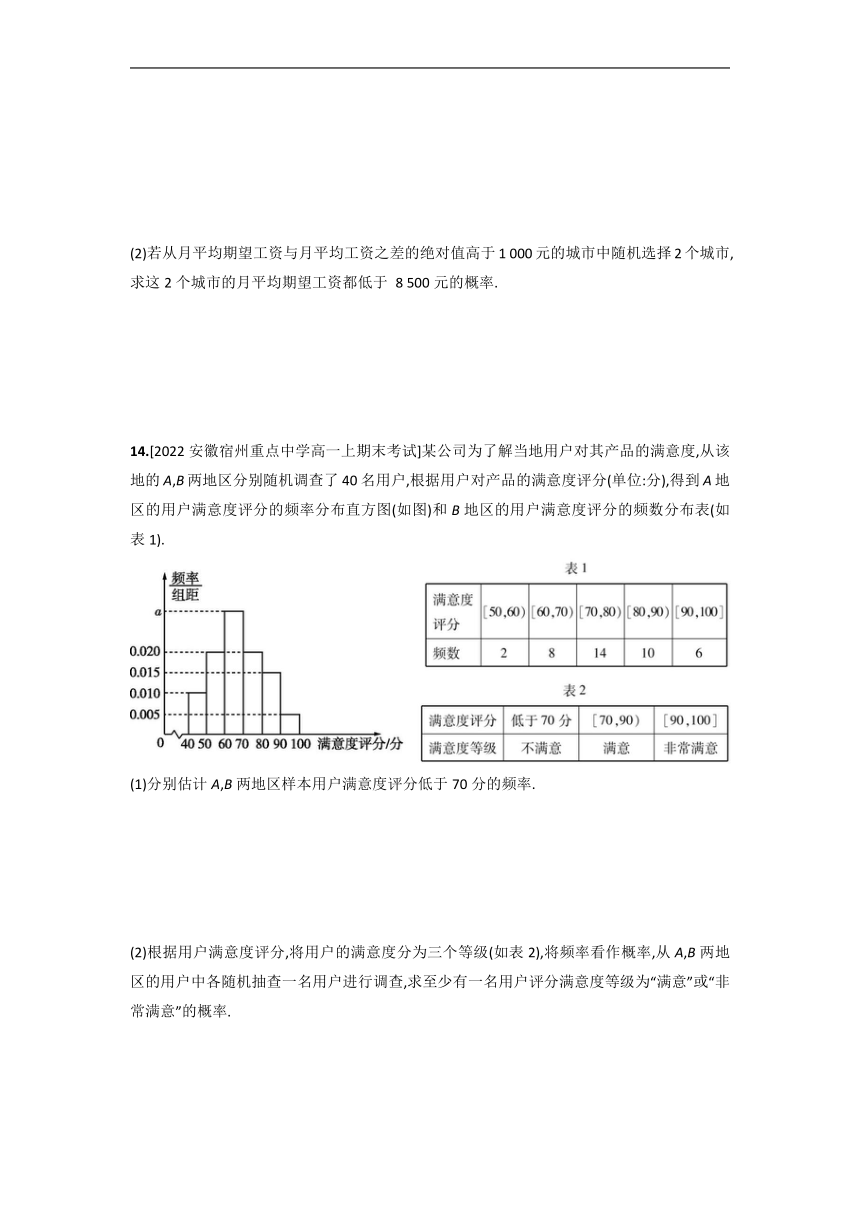
14.[2022安徽宿州重点中学高一上期末考试]某公司为了解当地用户对其产品的满意度,从该地的A,B两地区分别随机调查了40名用户,根据用户对产品的满意度评分(单位:分),得到A地区的用户满意度评分的频率分布直方图(如图)和B地区的用户满意度评分的频数分布表(如表1).
(1)分别估计A,B两地区样本用户满意度评分低于70分的频率.
(2)根据用户满意度评分,将用户的满意度分为三个等级(如表2),将频率看作概率,从A,B两地区的用户中各随机抽查一名用户进行调查,求至少有一名用户评分满意度等级为“满意”或“非常满意”的概率.
15. 某校高一年级为了提高教学质量,对老师命制的试卷提出要求,难度系数须控制在[0.65,0.7](难度系数是指学生得分的平均数与试卷总分的比值,例如:满分为100分的试卷平均分为68分,则难度系数为=0.68).某次数学考试(满分100分),王老师根据所带班级100名学生的等级来估计高一年级1 800人的数学成绩情况,已知学生的成绩分为A,B,C,D,E五个等级,统计数据如图所示.
根据图中的数据,回答下列问题:
(1)试估算该校高一年级学生的数学成绩等级为B的人数.
(2)若等级A,B,C,D,E分别对应90分、80分、70分、60分、50分,请问按王老师的估计,本次数学考试试卷的命制是否符合要求
(3)王老师决定从数学成绩等级为A,B的学生中按分层随机抽样选出6人分享学习经验,再从这6人中任选2人,求恰好抽到1名数学成绩等级为A的学生的概率.
参考答案
一、选择题
1.D 2.A 3.A 4.C 5.D 6.C
二、非选择题
7.
8.
9.
10.
11.(1)3个红球的分别记为1,2,3,1个黑球记为a,1个黄球记为b.
从袋中依次不放回地取出2个球,所包含的样本点为
(1,2),(1,3),(2,3),(1,a),(2,a),(3,a),(1,b),(2,b),(3,b),(a,b),(2,1),(3,1),
(3,2),(a,1),(a,2),(a,3),(b,1),(b,2),(b,3),(b,a),共20个,
有黄球的样本点为(1,b),(2,b),(3,b),(a,b),(b,1),(b,2),(b,3),(b,a),共8个,
所以这位顾客能获得一件价值10元的礼品的概率为.
(2)从袋中连续取两次球,每次取1球后放回,所包含的样本点为
(1,1),(1,2),(1,3),(1,a),(1,b),(2,1),(2,2),(2,3),(2,a),(2,b),
(3,1),(3,2),(3,3),(3,a),(3,b),(a,1),(a,2),(a,3),(a,a),(a,b),(b,1),(b,2),(b,3),(b,a),(b,b),共25个,
取出的2个球中没有红球的样本点为(a,a),(a,b),(b,a),(b,b),共4个,
所以这位顾客能获得一件价值50元的礼品的概率为<20%,
所以这位顾客获得一件价值50元的商品的可能性不会超过20%.
12.(1)由题意,知4+x+20+38+30=100,∴x=8.
在这100份作业中,大三学生的作业共3+6+15+y+12=(36+y)(份),
则大四学生的作业共(64-y)份.
∵选修该门课程的大三与大四学生的人数之比为3∶2,∴,解得y=24.
故大四学生作业共40份,其中,成绩在[60,70),[70,80)的作业份数分别为2,5,故成绩在[60,80)的作业共7份.
∴从选修该门课程的大四学生中随机选取1名,估计其作业成绩在[60,80)的概率为.
(2)由(1)可知,这100份作业中大三学生的作业共60份.
则估计大三学生作业的平均成绩为×55+×65+×75+×85+×95=81(分).
13.(1)设“该生选中月平均工资高于8 500元的城市”为事件E,
15个城市中月平均工资高于8 500元的有6个,
所以 P(E)=.
(2)月平均期望工资与月平均工资之差的绝对值高于1 000元的城市有6个,
其中月平均期望工资高于8 500元的有1个,记为A;月平均期望工资低于8 500元的有5个,记为B1,B2,B3,B4,B5.
选取2个城市的样本空间为
{AB1,AB2,AB3,AB4,AB5,B1B2,B1B3,B1B4,B1B5,B2B3,B2B4,B2B5,B3B4,B3B5,B4B5},
共15个样本点,其中2个城市的月平均期望工资都低于8 500元的样本空间为
{B1B2,B1B3,B1B4,B1B5,B2B3,B2B4,B2B5,B3B4,B3B5,B4B5},共10个样本点.
所以所求概率为.
14.(1)由题图可得(0.005+0.010+0.015+0.020×2+a)×10=1,解得a=0.030,
估计A地区样本用户满意度评分低于70分的频率为(0.010+0.020+0.030)×10=0.6,
估计B地区样本用户满意度评分低于70分的频率为=0.25.
(2)根据样本频率可以估计总体频率,记事件M表示“从A地区随机抽取一名用户满意度评级为不满意”,则P(M)=0.6.
记事件N表示“从B地区随机抽取一名用户满意度评级为不满意”,则P(N)=0.25.
易知事件M和事件N相互独立,则事件和事件相互独立.
记事件C表示“至少有一名用户评分满意度等级为‘满意’或‘非常满意’”,
则P(C)=1-P()=1-P(M)P(N)=1-0.6×0.25=0.85,
故至少有一名用户评分满意度等级为“满意”或“非常满意”的概率为0.85.
15.(1)高一年级学生的数学成绩等级为B的人数约为×1 800=252.
(2)王老师所带班级数学成绩的平均分为=67.4,
所以估计难度系数为=0.674,符合要求.
(3)按分层随机抽样,抽到的6人中数学成绩等级为A的有6×=2(人),编号分别为a,b,数学成绩等级为B的有6×=4(人),编号分别为1,2,3,4.
从6人中任选2人,其样本空间为{ab,a1,a2,a3,a4,b1,b2,b3,b4,12,13,14,23,24,34},共15个样本点.
选到的2人中恰有1名数学成绩等级为A,其样本空间为{a1,a2,a3,a4,b1,b2,b3,b4},共8个样本点,
所以恰好抽到1名数学成绩等级为A的概率为.
一、选择题
1.现有如表所示的五项运动供选择,记试验F“某人运动的总时长大于或等于60 min的运动组合方式”,则该试验中样本点的个数为( )
A运动 B运动 C运动 D运动 E运动
7:00~8:00 8:00~9:00 9:00~10:00 10:00~11:00 11:00~12:00
30 min 20 min 40 min 30 min 30 min
A.7 B.6 C.10 D.23
2.《易·系辞上》有“河出图,洛出书”之说,河图、洛书是中华文化、阴阳五行术数之源,其中河图的排列结构是一、六在后,二、七在前,三、八在左,四、九在右,五、十背中,如图,白圈为阳数,黑点为阴数,若从阴数和阳数中各取一数,则其差的绝对值为5的概率为( )
A. B. C. D.
3.我国古代数学著作《周髀算经》中有这样的表述:“若求邪至日者,以日下为勾,日高为股.勾股各自乘,并而开方除之,得邪至日.”这就是我们熟知的勾股定理.勾股数组是指满足a2+b2=c2的正整数组(a,b,c).现将一枚质地均匀的骰子抛掷三次,则三次向上的点数恰好组成勾股数组的概率是( )
A. B. C. D.
4.法国有个名人叫作布莱士·帕斯卡,他认识一个赌徒,这个赌徒向他提出一个问题:甲、乙两个人赌博,在他们下赌金之后,约定谁先赢满5局,谁就获得全部赌金700法郎,赌了半天,甲赢了4局,乙赢了3局,时间很晚了,他们都不想再赌下去,但是不知道赌金如何分配才合理.假设每局甲、乙两人获胜的概率均为,且每局输赢相互独立,那么这700法郎比较合理的分配方法是( )
A.甲400法郎,乙300法郎
B.甲500法郎,乙200法郎
C.甲525法郎,乙175法郎
D.甲350法郎,乙350法郎
5.数学上有种水仙花数,它是指各位数字的立方和等于其本身的三位数.水仙花数共有4个,其中仅有1个在区间(150,160)内,我们姑且称它为“水仙四妹”,则从集合{147,152,154,157,“水仙四妹”}的5个元素中任意取3个整数,则这3个整数中含有“水仙四妹”,且其余两个整数至少有一个比“水仙四妹”小的概率是( )
A. B. C. D.
6.一个三位自然数,百位、十位、个位上的数字依次为a,b,c,当且仅当a>b,b
C. D.
二、非选择题
7.用数字1,2组成一个四位数,则数字1,2都出现的概率为 .
8.从正六边形的6个顶点中随机选出4个,以它们作为顶点的四边形是矩形的概率为 .
9.古代“五行”学说认为“物质分金、木、水、火、土五种属性,金克木,木克土,土克水,水克火,火克金”,从五种不同属性的物质中随机抽取两种,则抽取的两种物质不相克的概率为 .
10.算盘是中国传统的计算工具.下图是一把算盘的初始状态,自右向左,分别是个位、十位、百位……,上面1粒珠(简称上珠)代表5,下面1粒珠(简称下珠)代表1,即5粒下珠的大小等于同组1粒上珠的大小.现从个位、十位、百位和千位这四组中随机拨动2粒珠(约定每档的上珠中最上面的1粒和下珠中最下面的1粒不使用,上珠只能往下拨,下珠只能往上拨),则算盘表示的整数能够被5整除的概率为 .
11.[2022黑龙江哈六中高二上期中考试]某商场做促销活动,顾客每购满100元可抽奖一次.在一个口袋内装有除颜色外其余完全相同的5个小球,其中3个红球、1个黑球、1个黄球.某顾客购满100元,可抽奖一次.
(1)若从中依次不放回地取出2个球,取出的球中有黄球,则送一件价值10元的礼品,求这位顾客能获得一件价值10元的礼品的概率;
(2)若从口袋中连续取两次球,每次取1个球后放回,当取出的2个球中没有红球时,送一件价值50元的礼品,问这位顾客获得一件价值50元的礼品的可能性会超过20%吗
12.为了让建筑类学生了解古建筑设计与构造的原理,某建筑大学为大三和大四的学生开设了一门选修课程《营造法式及其注释》.为检测学生学习效果,要求所有选修该门课程的学生完成“应用营造法式独立制作一件古建筑模型”的作业.已知选修该门课程的大三与大四学生的人数之比为3∶2,现用分层随机抽样的方法从所有作业中随机抽取100份(每位学生均上交一份作业),并评出成绩,得到如下频数分布表.
成绩/分 [50,60) [60,70) [70,80) [80,90) [90,100]
频数(不分年级) 4 x 20 38 30
频数(大三年级) 3 6 15 y 12
(1)求x,y的值,若以频率作为概率,从选修该门课程的大四学生中随机选取1名,试估计该学生的作业成绩在[60,80)的概率;
(2)估计这100份作业中大三学生作业的平均成绩(同一组中的数据用该组区间的中点值为代表).
13.随着经济全球化、信息化,企业之间的竞争从资源的争夺转向人才的竞争.吸引、留住、培养和用好人才成为人力资源管理的战略目标和紧迫任务.在此背景下,某信息网站在15个城市对刚毕业的大学生的月平均工资和月平均期望工资进行了调查,数据如图所示.
(1)若某大学毕业生从这15个城市中随机选择 1个城市就业,求该生选中月平均工资高于 8 500元的城市的概率;
(2)若从月平均期望工资与月平均工资之差的绝对值高于1 000元的城市中随机选择2个城市,求这2个城市的月平均期望工资都低于 8 500元的概率.
14.[2022安徽宿州重点中学高一上期末考试]某公司为了解当地用户对其产品的满意度,从该地的A,B两地区分别随机调查了40名用户,根据用户对产品的满意度评分(单位:分),得到A地区的用户满意度评分的频率分布直方图(如图)和B地区的用户满意度评分的频数分布表(如表1).
(1)分别估计A,B两地区样本用户满意度评分低于70分的频率.
(2)根据用户满意度评分,将用户的满意度分为三个等级(如表2),将频率看作概率,从A,B两地区的用户中各随机抽查一名用户进行调查,求至少有一名用户评分满意度等级为“满意”或“非常满意”的概率.
15. 某校高一年级为了提高教学质量,对老师命制的试卷提出要求,难度系数须控制在[0.65,0.7](难度系数是指学生得分的平均数与试卷总分的比值,例如:满分为100分的试卷平均分为68分,则难度系数为=0.68).某次数学考试(满分100分),王老师根据所带班级100名学生的等级来估计高一年级1 800人的数学成绩情况,已知学生的成绩分为A,B,C,D,E五个等级,统计数据如图所示.
根据图中的数据,回答下列问题:
(1)试估算该校高一年级学生的数学成绩等级为B的人数.
(2)若等级A,B,C,D,E分别对应90分、80分、70分、60分、50分,请问按王老师的估计,本次数学考试试卷的命制是否符合要求
(3)王老师决定从数学成绩等级为A,B的学生中按分层随机抽样选出6人分享学习经验,再从这6人中任选2人,求恰好抽到1名数学成绩等级为A的学生的概率.
参考答案
一、选择题
1.D 2.A 3.A 4.C 5.D 6.C
二、非选择题
7.
8.
9.
10.
11.(1)3个红球的分别记为1,2,3,1个黑球记为a,1个黄球记为b.
从袋中依次不放回地取出2个球,所包含的样本点为
(1,2),(1,3),(2,3),(1,a),(2,a),(3,a),(1,b),(2,b),(3,b),(a,b),(2,1),(3,1),
(3,2),(a,1),(a,2),(a,3),(b,1),(b,2),(b,3),(b,a),共20个,
有黄球的样本点为(1,b),(2,b),(3,b),(a,b),(b,1),(b,2),(b,3),(b,a),共8个,
所以这位顾客能获得一件价值10元的礼品的概率为.
(2)从袋中连续取两次球,每次取1球后放回,所包含的样本点为
(1,1),(1,2),(1,3),(1,a),(1,b),(2,1),(2,2),(2,3),(2,a),(2,b),
(3,1),(3,2),(3,3),(3,a),(3,b),(a,1),(a,2),(a,3),(a,a),(a,b),(b,1),(b,2),(b,3),(b,a),(b,b),共25个,
取出的2个球中没有红球的样本点为(a,a),(a,b),(b,a),(b,b),共4个,
所以这位顾客能获得一件价值50元的礼品的概率为<20%,
所以这位顾客获得一件价值50元的商品的可能性不会超过20%.
12.(1)由题意,知4+x+20+38+30=100,∴x=8.
在这100份作业中,大三学生的作业共3+6+15+y+12=(36+y)(份),
则大四学生的作业共(64-y)份.
∵选修该门课程的大三与大四学生的人数之比为3∶2,∴,解得y=24.
故大四学生作业共40份,其中,成绩在[60,70),[70,80)的作业份数分别为2,5,故成绩在[60,80)的作业共7份.
∴从选修该门课程的大四学生中随机选取1名,估计其作业成绩在[60,80)的概率为.
(2)由(1)可知,这100份作业中大三学生的作业共60份.
则估计大三学生作业的平均成绩为×55+×65+×75+×85+×95=81(分).
13.(1)设“该生选中月平均工资高于8 500元的城市”为事件E,
15个城市中月平均工资高于8 500元的有6个,
所以 P(E)=.
(2)月平均期望工资与月平均工资之差的绝对值高于1 000元的城市有6个,
其中月平均期望工资高于8 500元的有1个,记为A;月平均期望工资低于8 500元的有5个,记为B1,B2,B3,B4,B5.
选取2个城市的样本空间为
{AB1,AB2,AB3,AB4,AB5,B1B2,B1B3,B1B4,B1B5,B2B3,B2B4,B2B5,B3B4,B3B5,B4B5},
共15个样本点,其中2个城市的月平均期望工资都低于8 500元的样本空间为
{B1B2,B1B3,B1B4,B1B5,B2B3,B2B4,B2B5,B3B4,B3B5,B4B5},共10个样本点.
所以所求概率为.
14.(1)由题图可得(0.005+0.010+0.015+0.020×2+a)×10=1,解得a=0.030,
估计A地区样本用户满意度评分低于70分的频率为(0.010+0.020+0.030)×10=0.6,
估计B地区样本用户满意度评分低于70分的频率为=0.25.
(2)根据样本频率可以估计总体频率,记事件M表示“从A地区随机抽取一名用户满意度评级为不满意”,则P(M)=0.6.
记事件N表示“从B地区随机抽取一名用户满意度评级为不满意”,则P(N)=0.25.
易知事件M和事件N相互独立,则事件和事件相互独立.
记事件C表示“至少有一名用户评分满意度等级为‘满意’或‘非常满意’”,
则P(C)=1-P()=1-P(M)P(N)=1-0.6×0.25=0.85,
故至少有一名用户评分满意度等级为“满意”或“非常满意”的概率为0.85.
15.(1)高一年级学生的数学成绩等级为B的人数约为×1 800=252.
(2)王老师所带班级数学成绩的平均分为=67.4,
所以估计难度系数为=0.674,符合要求.
(3)按分层随机抽样,抽到的6人中数学成绩等级为A的有6×=2(人),编号分别为a,b,数学成绩等级为B的有6×=4(人),编号分别为1,2,3,4.
从6人中任选2人,其样本空间为{ab,a1,a2,a3,a4,b1,b2,b3,b4,12,13,14,23,24,34},共15个样本点.
选到的2人中恰有1名数学成绩等级为A,其样本空间为{a1,a2,a3,a4,b1,b2,b3,b4},共8个样本点,
所以恰好抽到1名数学成绩等级为A的概率为.
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
