人教A版数学选修2-1 3.2.5 空间向量与空间角问题 课件(共23张PPT)
文档属性
| 名称 | 人教A版数学选修2-1 3.2.5 空间向量与空间角问题 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 783.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-07 00:00:00 | ||
图片预览


文档简介
(共23张PPT)
3.2.5空间向量与空间角问题
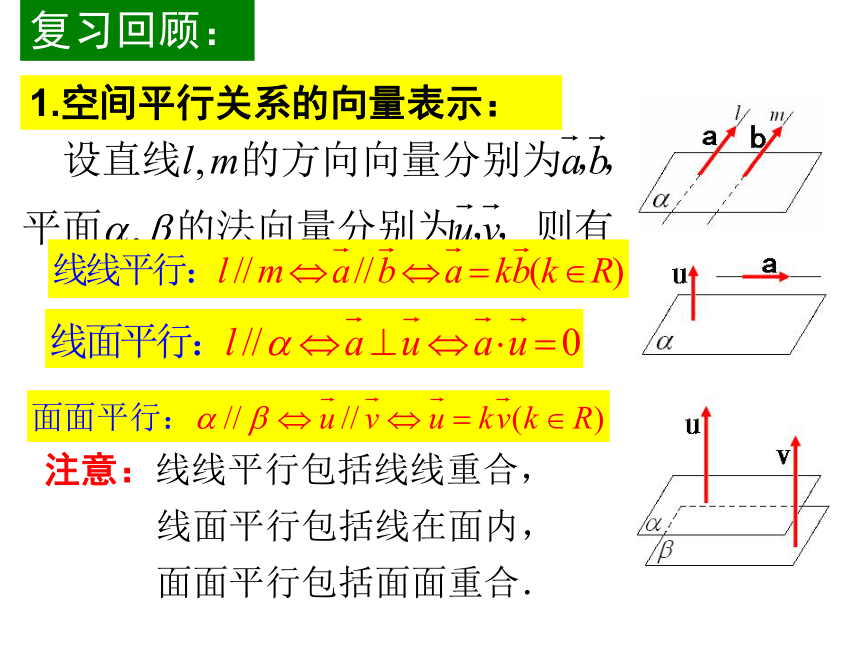
1.空间平行关系的向量表示:
复习回顾:
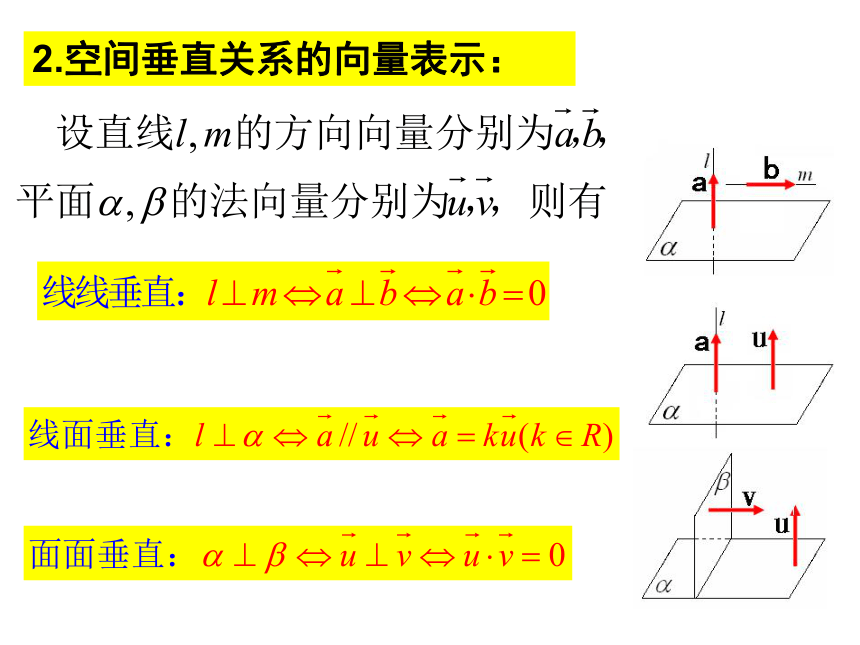
2.空间垂直关系的向量表示:
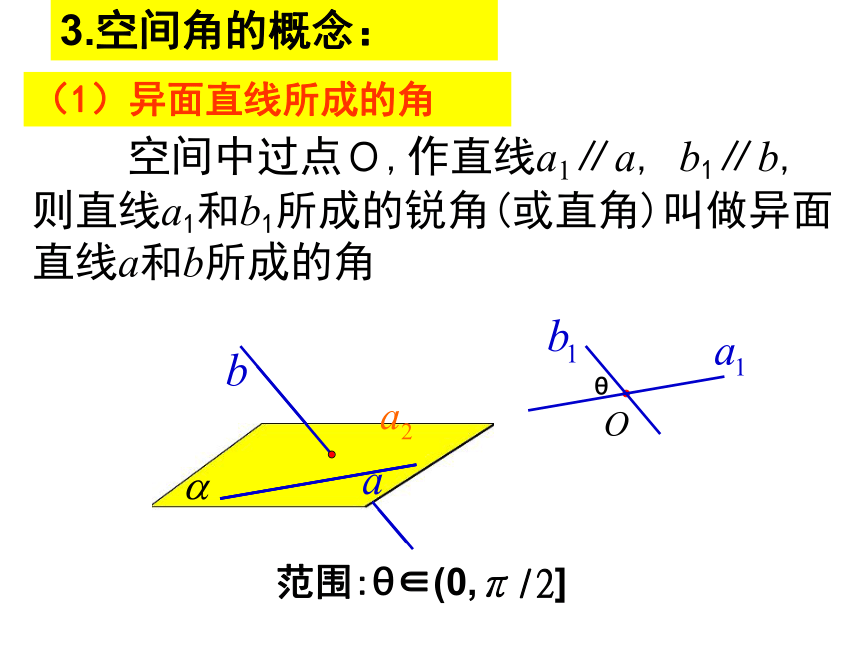
(1)异面直线所成的角
范围:θ∈(0,π/2]
则直线a1和b1所成的锐角(或直角)叫做异面直线a和b所成的角
空间中过点O,作直线a1∥a, b1∥b,
θ
3.空间角的概念:
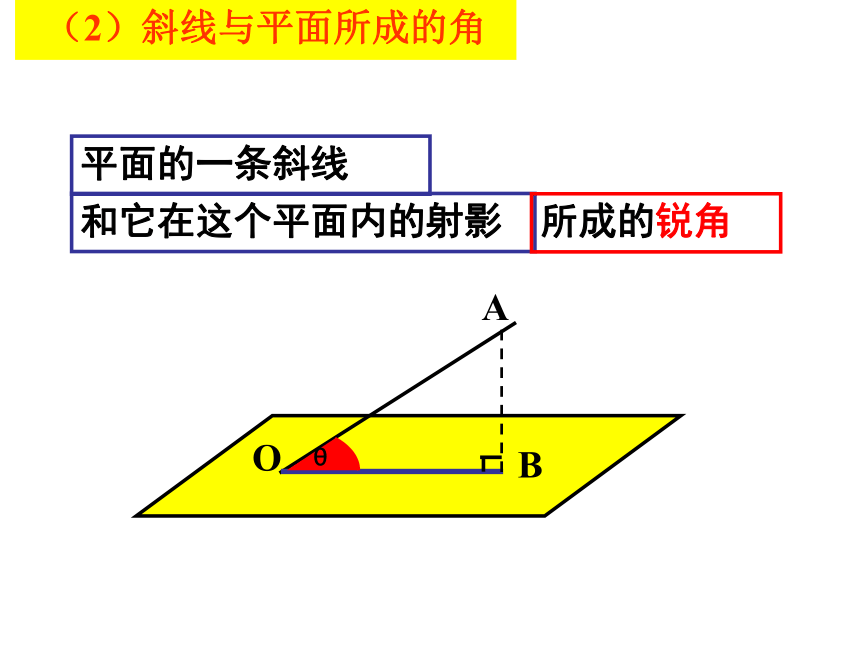
(2)斜线与平面所成的角
平面的一条斜线
和它在这个平面内的射影
所成的锐角
A
O
B
θ
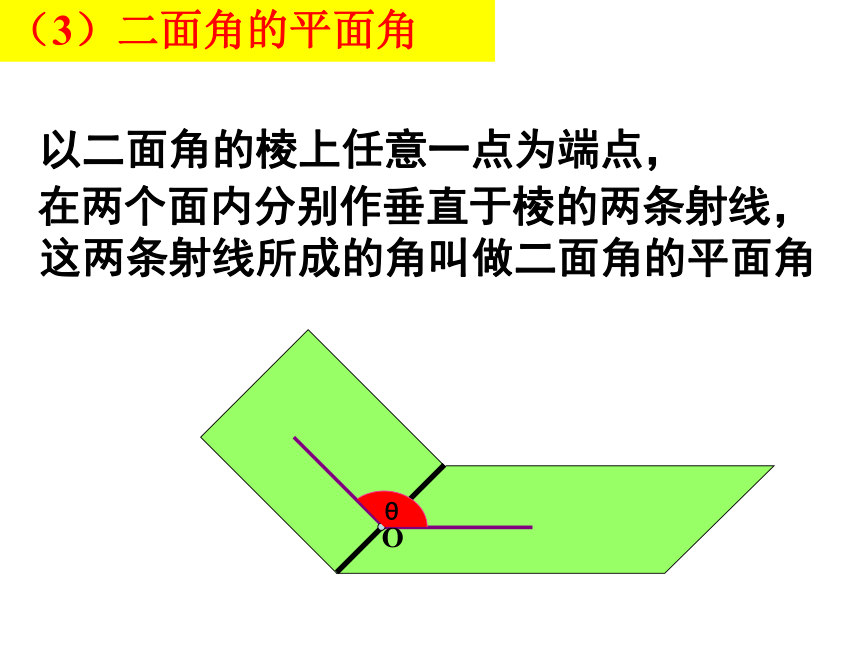
(3)二面角的平面角
以二面角的棱上任意一点为端点,
在两个面内分别作垂直于棱的两条射线,
这两条射线所成的角叫做二面角的平面角
O
θ
l
m
l
m
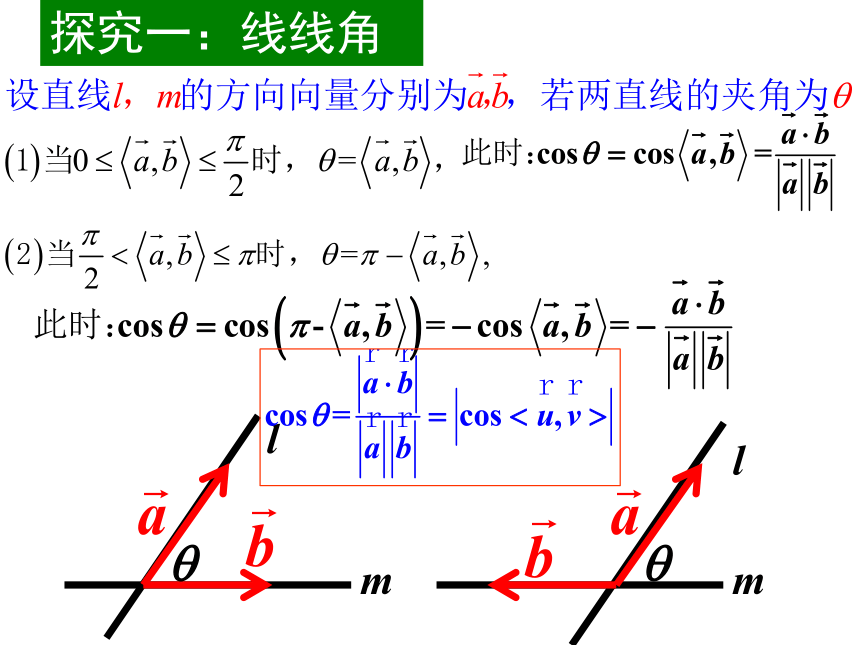
探究一:线线角
例1:如图,在正方体ABCD-A1B1C1D1中,E,F分别是AB,A1D1的中点,求直线EF与BD1所成角的余弦值.
l
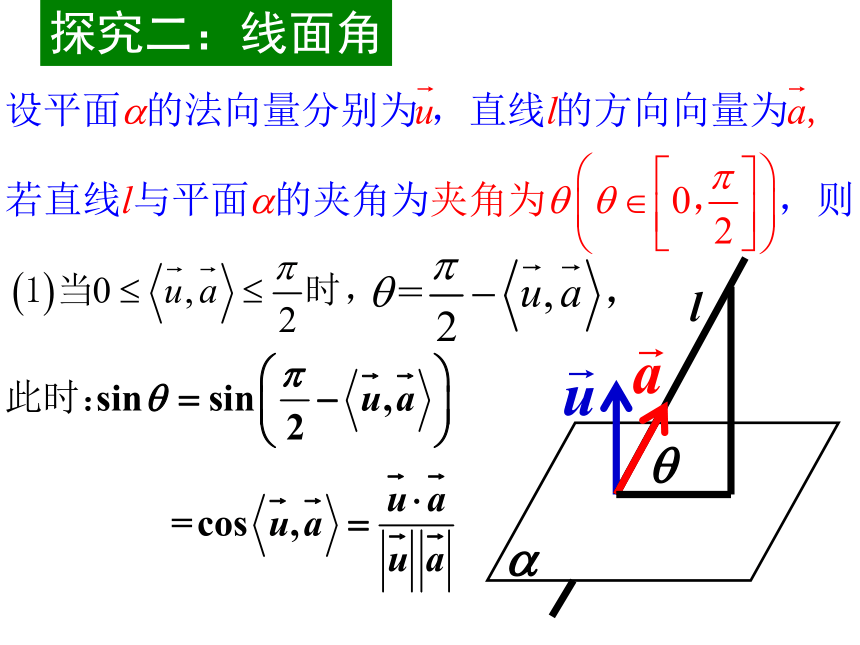
探究二:线面角
l
例2:正方体ABCD-A1B1C1D1的棱长为1,点E、F分别为CD、DD1的中点,
求直线B1C1与平面AB1C所成的角的正弦值;
A
A1
C1
B1
D
C
B
D1
例2:求直线B1C1与平面AB1C所成的角的正弦值;
x
y
z
A
D
B
A1
D1
C1
B1
解: (1)以点A为坐标原点建立空间直角坐标系,如图所示,则:
A(0,0,0)
B1(1,0,1)
C(1,1,0)
C1(1,1,1)
设平面AB1C的法向量为n=(x1,y1,z1),
所以
X1+z1=0
X1+y1=0
取x1=1,得y1=z1=-1
故n=(1,-1,-1)
C
故所求直线B1C1与平面AB1C所成的角的正弦值为
注意法向量的方向:一进一出,两平面的夹角等于法向量夹角
探究三:面面角
注意法向量的方向:同进同出,两平面的夹角等于
法向量夹角的补角
例3:正方体ABCD-A1B1C1D1的棱长为1,点E、F分别为CD、DD1的中点,
求二面角F-AE-D的余弦值。
A
A1
C1
B1
D
C
B
D1
E
F
x
y
z
A
D
C
A1
D1
C1
B1
B
F
E
例3 点E、F分别为CD、DD1的中点,求二面角F-AE-D的余弦值。
取y2=1,得x2=z2=-2
(2)由题意知
设平面AEF的法向量为m=(x2,y2,z2),
所以
故m=(-2, 1,-2)
又平面AED的法向量为AA1=(0,0,1)
观察图形知,二面角F-AE-D为锐角,所以所求二面角F-AE-D的余弦值为
一、.空间夹角的向量表示:
小结:
θ
θ
3.2.5空间向量与空间角问题
1.空间平行关系的向量表示:
复习回顾:
2.空间垂直关系的向量表示:
(1)异面直线所成的角
范围:θ∈(0,π/2]
则直线a1和b1所成的锐角(或直角)叫做异面直线a和b所成的角
空间中过点O,作直线a1∥a, b1∥b,
θ
3.空间角的概念:
(2)斜线与平面所成的角
平面的一条斜线
和它在这个平面内的射影
所成的锐角
A
O
B
θ
(3)二面角的平面角
以二面角的棱上任意一点为端点,
在两个面内分别作垂直于棱的两条射线,
这两条射线所成的角叫做二面角的平面角
O
θ
l
m
l
m
探究一:线线角
例1:如图,在正方体ABCD-A1B1C1D1中,E,F分别是AB,A1D1的中点,求直线EF与BD1所成角的余弦值.
l
探究二:线面角
l
例2:正方体ABCD-A1B1C1D1的棱长为1,点E、F分别为CD、DD1的中点,
求直线B1C1与平面AB1C所成的角的正弦值;
A
A1
C1
B1
D
C
B
D1
例2:求直线B1C1与平面AB1C所成的角的正弦值;
x
y
z
A
D
B
A1
D1
C1
B1
解: (1)以点A为坐标原点建立空间直角坐标系,如图所示,则:
A(0,0,0)
B1(1,0,1)
C(1,1,0)
C1(1,1,1)
设平面AB1C的法向量为n=(x1,y1,z1),
所以
X1+z1=0
X1+y1=0
取x1=1,得y1=z1=-1
故n=(1,-1,-1)
C
故所求直线B1C1与平面AB1C所成的角的正弦值为
注意法向量的方向:一进一出,两平面的夹角等于法向量夹角
探究三:面面角
注意法向量的方向:同进同出,两平面的夹角等于
法向量夹角的补角
例3:正方体ABCD-A1B1C1D1的棱长为1,点E、F分别为CD、DD1的中点,
求二面角F-AE-D的余弦值。
A
A1
C1
B1
D
C
B
D1
E
F
x
y
z
A
D
C
A1
D1
C1
B1
B
F
E
例3 点E、F分别为CD、DD1的中点,求二面角F-AE-D的余弦值。
取y2=1,得x2=z2=-2
(2)由题意知
设平面AEF的法向量为m=(x2,y2,z2),
所以
故m=(-2, 1,-2)
又平面AED的法向量为AA1=(0,0,1)
观察图形知,二面角F-AE-D为锐角,所以所求二面角F-AE-D的余弦值为
一、.空间夹角的向量表示:
小结:
θ
θ
