6.4.3余弦定理、正弦定理 教案(表格式)
文档属性
| 名称 | 6.4.3余弦定理、正弦定理 教案(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 160.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-15 00:00:00 | ||
图片预览


文档简介
铜仁市第十五中学课时教学设计
课题名称 6.4.3 余弦定理、正弦定理 余弦定理、正弦定理的应用举例 授课教师
学习目标: 知识目标: 1.进一步熟悉余弦定理、正弦定理; 2.了解常用的测量相关术语; 3.能运用余弦定理、正弦定理等知识和方法解决有关距离、高度、角度的实际问题。 素养目标: 通过应用举例的教学,进一步培养学生的数学抽象;.逻辑推理;数学运算;数学建模核心素养。
重点、难点: 重点:实际问题中抽象出一个或几个三角形,然后逐个解决三角形,得到实际问题的解。 难点:根据题意画出示意图,建立数学模型。
三、教学方法:以学生为主体,采用诱思探究式教学。
四、学习方法:学生独立思考,合作探究学习。
五、教学流程:创设情境,引入课题→梳理基本概念→正、余弦定理的实际应用→小结→作业布置
六、学习过程:
教学环节 教师活动 学生活动 设计意图
创设情境引发问题 同学们,众所周知,古有诸亮夜观天象,和七次下西洋,徐霞客游历多国名山大川。他们对我天文观测,航海和地理测量方面作出了突出奉献。随着当代科技与数学的开展,我们现在掌握了更先进的方法来认识自然。我们这一章解三角形的理论就在其中发挥了重要作用。 在测量过程中,早在1671年,两个法国天文学家就测出了地球与月亮之间的距离大约为385400km。他们是怎样测出两者之间的距离呢?带着这一系列问题,我们进入今天的数学学习。 学生聆听思考 引入这节课所讲容,并给同学提出疑问。
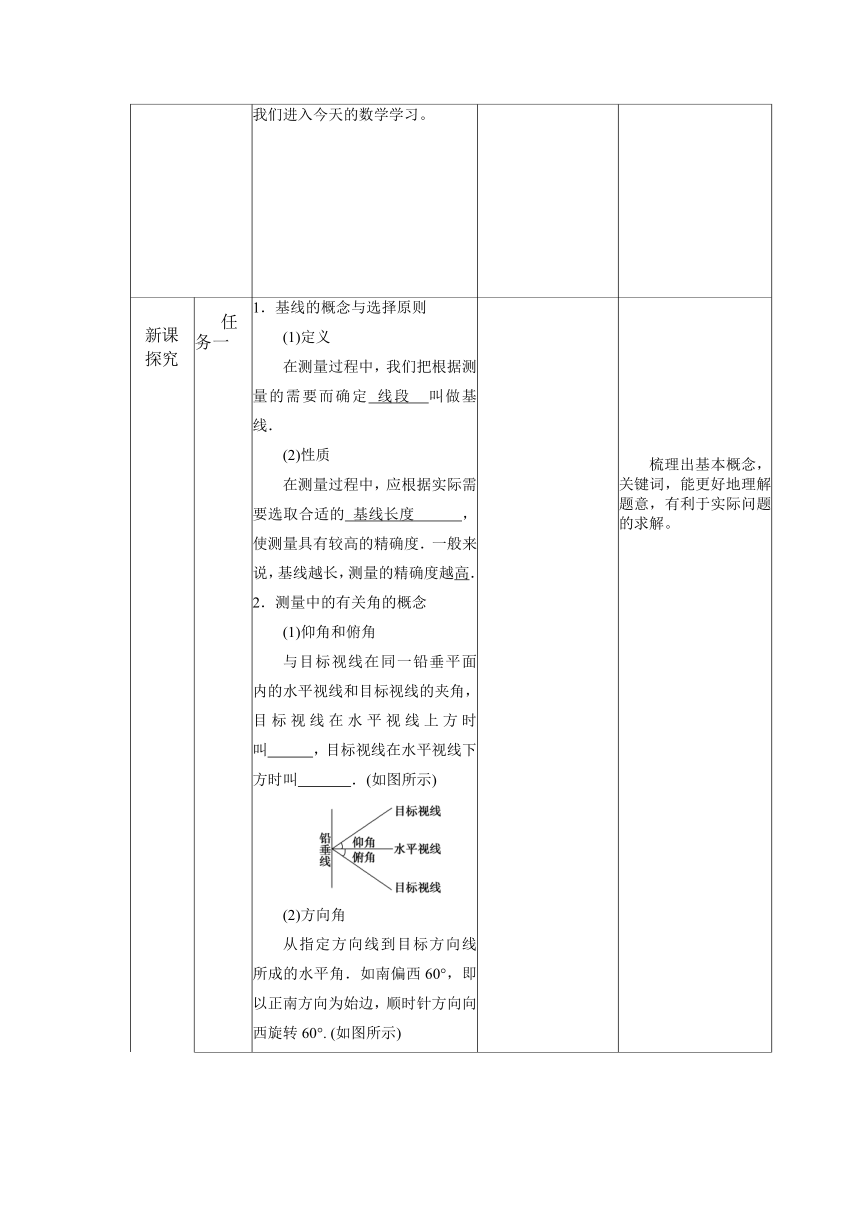
新课 探究 任务一 1.基线的概念与选择原则 (1)定义 在测量过程中,我们把根据测量的需要而确定 线段 叫做基线. (2)性质 在测量过程中,应根据实际需要选取合适的 基线长度 ,使测量具有较高的精确度.一般来说,基线越长,测量的精确度越高. 2.测量中的有关角的概念 (1)仰角和俯角 与目标视线在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线上方时叫 ,目标视线在水平视线下方时叫 .(如图所示) (2)方向角 从指定方向线到目标方向线所成的水平角.如南偏西60°,即以正南方向为始边,顺时针方向向西旋转60°. (如图所示) 梳理出基本概念,关键词,能更好地理解题意,有利于实际问题的求解。
任务二 类型一 距离问题 例1 如图, A,B两点都在河的对岸(不可到达),设计一种测量A,B两点间的距离的方法.并求出A,B间的距离。 思考:在上述测量方案下,还有其他计算A,B两点间距离的方法吗? 类型二 底部不可到达的建筑物的高度 例2 如图,AB是底部B不可到达的一座建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法.并求出建筑物的高度。 类型三 角度问题 例3.位于某海域A处的甲船获悉,在其正东方向相距20 n mile的B处有一艘渔船遇险后抛锚等待营救。甲船立即前往营救,同时把消息告知位于甲船南偏西,且与甲船相距7 n mile的C处的乙船,那么乙船前往营救遇险渔船时的目标方向线(由观测点看目标的视线)的方向是北偏东多少度(精确到 )?需要航行的距离是多少海里(精确到1 n mile)? 认真思考求解的一般步骤和方法,找出其中的规律。 交给同学解答一般解三角形实际问题中测量距离的求解方法,求解测量距离问题的方法是:选择合适的辅助测量点,构造三角形,将问题转化为求某个三角形的边长问题,从而利用正、余弦定理求解.构造数学模型时,尽量把已知元素放在同一个三角形中.让同学们了解到解三角形在实际中的应用是很广泛的。 高度的测量主要是一些底部不能到达或者无法直接测量的物体的高度问题.常用正弦定理或余弦定理计算出物体的顶部或底部到一个可到达的点之间的距离,然后转化为解直角三角形的问题. 测量角度问题的关键是在弄清题意的基础上,画出表示实际问题的图形,在图形中标出相关的角和距离. (2)根据实际选择正弦定理或余弦定理解三角形,然后将解得的结果转化为实际问题的解.
迁移应用 【跟踪训练】1 如图,若小河两岸平行,为了知道河对岸两棵树C,D(CD与河岸平行)之间的距离,选取岸边两点A,B(AB与河岸平行),测得数据:AB=6 m,∠ABD=60°,∠DBC=90°,∠DAB=75°,试求C,D之间的距离. 【跟踪训练】2 如图,要在山坡上A,B两处测量与地面垂直的铁塔CD的高,由A,B两处测得塔顶C的仰角分别为60°和45°,AB长为40 m,斜坡与水平面成30°角,则铁塔CD的高为________m.
拓展提升 【跟踪训练】3 地图测绘人员在点A测得某一目标参照物P在他的北偏东30°的方向,且距离为40 m,之后该测绘人员沿正北方向行走了40 m,达到点B.试确定此时目标参照物P在他北偏东的度数以及他与目标参照物P的距离.
总结反思感悟升华 拿到一个实际应用题目,我们要三步走: 第一步要认真读题,找出题目中的条件和所求问题。 第二步,把所求的边放到一个三角形中,并观察该三角形的条件能否求解。 第三步,如果条件缺乏,把所需条件再放到一个条件多的三角形中求解。最终得到所求边长。 希望同学们学习了今天的内容,能够灵活掌握正弦定理、余弦定理解题的根本分析方法和步骤。并且在遇到现实中一些问题时,能的用我们学到的数学知识加以求解,到达学以致用的效果。 使学生熟悉解题的过程,加深理解。
布置作业 教材53页 习题6.4 8、9题
板书设计
教学反思 正弦定理要求学生综合运用正弦定理和内角和定理等众多基础知识解决几何问题和实际应用问题,学生已具备初步的数学建模能力,会从简单的实际问题中抽象出数学模型完成教学目标。
课题名称 6.4.3 余弦定理、正弦定理 余弦定理、正弦定理的应用举例 授课教师
学习目标: 知识目标: 1.进一步熟悉余弦定理、正弦定理; 2.了解常用的测量相关术语; 3.能运用余弦定理、正弦定理等知识和方法解决有关距离、高度、角度的实际问题。 素养目标: 通过应用举例的教学,进一步培养学生的数学抽象;.逻辑推理;数学运算;数学建模核心素养。
重点、难点: 重点:实际问题中抽象出一个或几个三角形,然后逐个解决三角形,得到实际问题的解。 难点:根据题意画出示意图,建立数学模型。
三、教学方法:以学生为主体,采用诱思探究式教学。
四、学习方法:学生独立思考,合作探究学习。
五、教学流程:创设情境,引入课题→梳理基本概念→正、余弦定理的实际应用→小结→作业布置
六、学习过程:
教学环节 教师活动 学生活动 设计意图
创设情境引发问题 同学们,众所周知,古有诸亮夜观天象,和七次下西洋,徐霞客游历多国名山大川。他们对我天文观测,航海和地理测量方面作出了突出奉献。随着当代科技与数学的开展,我们现在掌握了更先进的方法来认识自然。我们这一章解三角形的理论就在其中发挥了重要作用。 在测量过程中,早在1671年,两个法国天文学家就测出了地球与月亮之间的距离大约为385400km。他们是怎样测出两者之间的距离呢?带着这一系列问题,我们进入今天的数学学习。 学生聆听思考 引入这节课所讲容,并给同学提出疑问。
新课 探究 任务一 1.基线的概念与选择原则 (1)定义 在测量过程中,我们把根据测量的需要而确定 线段 叫做基线. (2)性质 在测量过程中,应根据实际需要选取合适的 基线长度 ,使测量具有较高的精确度.一般来说,基线越长,测量的精确度越高. 2.测量中的有关角的概念 (1)仰角和俯角 与目标视线在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线上方时叫 ,目标视线在水平视线下方时叫 .(如图所示) (2)方向角 从指定方向线到目标方向线所成的水平角.如南偏西60°,即以正南方向为始边,顺时针方向向西旋转60°. (如图所示) 梳理出基本概念,关键词,能更好地理解题意,有利于实际问题的求解。
任务二 类型一 距离问题 例1 如图, A,B两点都在河的对岸(不可到达),设计一种测量A,B两点间的距离的方法.并求出A,B间的距离。 思考:在上述测量方案下,还有其他计算A,B两点间距离的方法吗? 类型二 底部不可到达的建筑物的高度 例2 如图,AB是底部B不可到达的一座建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法.并求出建筑物的高度。 类型三 角度问题 例3.位于某海域A处的甲船获悉,在其正东方向相距20 n mile的B处有一艘渔船遇险后抛锚等待营救。甲船立即前往营救,同时把消息告知位于甲船南偏西,且与甲船相距7 n mile的C处的乙船,那么乙船前往营救遇险渔船时的目标方向线(由观测点看目标的视线)的方向是北偏东多少度(精确到 )?需要航行的距离是多少海里(精确到1 n mile)? 认真思考求解的一般步骤和方法,找出其中的规律。 交给同学解答一般解三角形实际问题中测量距离的求解方法,求解测量距离问题的方法是:选择合适的辅助测量点,构造三角形,将问题转化为求某个三角形的边长问题,从而利用正、余弦定理求解.构造数学模型时,尽量把已知元素放在同一个三角形中.让同学们了解到解三角形在实际中的应用是很广泛的。 高度的测量主要是一些底部不能到达或者无法直接测量的物体的高度问题.常用正弦定理或余弦定理计算出物体的顶部或底部到一个可到达的点之间的距离,然后转化为解直角三角形的问题. 测量角度问题的关键是在弄清题意的基础上,画出表示实际问题的图形,在图形中标出相关的角和距离. (2)根据实际选择正弦定理或余弦定理解三角形,然后将解得的结果转化为实际问题的解.
迁移应用 【跟踪训练】1 如图,若小河两岸平行,为了知道河对岸两棵树C,D(CD与河岸平行)之间的距离,选取岸边两点A,B(AB与河岸平行),测得数据:AB=6 m,∠ABD=60°,∠DBC=90°,∠DAB=75°,试求C,D之间的距离. 【跟踪训练】2 如图,要在山坡上A,B两处测量与地面垂直的铁塔CD的高,由A,B两处测得塔顶C的仰角分别为60°和45°,AB长为40 m,斜坡与水平面成30°角,则铁塔CD的高为________m.
拓展提升 【跟踪训练】3 地图测绘人员在点A测得某一目标参照物P在他的北偏东30°的方向,且距离为40 m,之后该测绘人员沿正北方向行走了40 m,达到点B.试确定此时目标参照物P在他北偏东的度数以及他与目标参照物P的距离.
总结反思感悟升华 拿到一个实际应用题目,我们要三步走: 第一步要认真读题,找出题目中的条件和所求问题。 第二步,把所求的边放到一个三角形中,并观察该三角形的条件能否求解。 第三步,如果条件缺乏,把所需条件再放到一个条件多的三角形中求解。最终得到所求边长。 希望同学们学习了今天的内容,能够灵活掌握正弦定理、余弦定理解题的根本分析方法和步骤。并且在遇到现实中一些问题时,能的用我们学到的数学知识加以求解,到达学以致用的效果。 使学生熟悉解题的过程,加深理解。
布置作业 教材53页 习题6.4 8、9题
板书设计
教学反思 正弦定理要求学生综合运用正弦定理和内角和定理等众多基础知识解决几何问题和实际应用问题,学生已具备初步的数学建模能力,会从简单的实际问题中抽象出数学模型完成教学目标。
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
