数学人教A版(2019)选择性必修第一册2.2.2直线的两点式方程 课件(共25张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.2.2直线的两点式方程 课件(共25张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 37.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-15 11:51:54 | ||
图片预览








文档简介
(共25张PPT)
一、直线方程的点斜式、斜截式?
温故知新
二、求直线方程的要点:
温故知新
三、求直线方程的注意点:
温故知新
【探究】我们知道已知两点也可以确定一条直线,在平面直角坐标系中,
给定一个点P0(x0,y0)和斜率k,可得出直线方程.若给定直线上
两点P1(x1,y1),P2(x2,y2)(x1≠x2,y1≠y2),能否得出直线的
方程呢?
温故知新
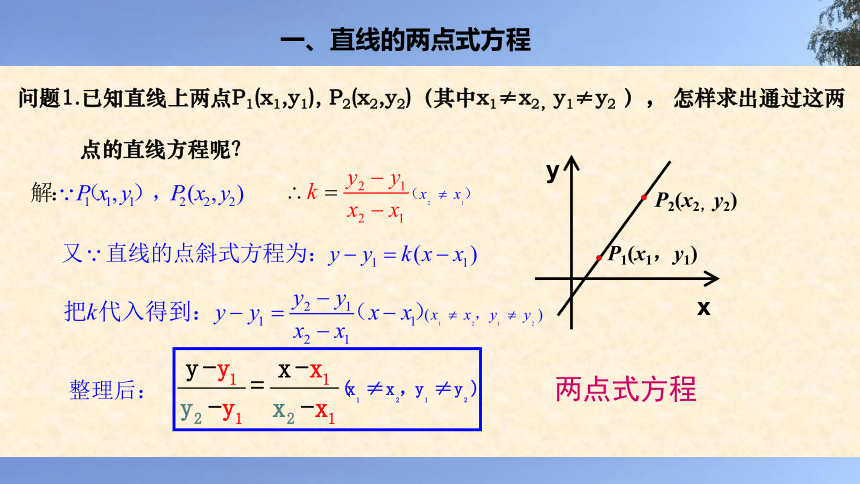
一、直线的两点式方程
问题1.已知直线上两点P1(x1,y1), P2(x2,y2)(其中x1≠x2,y1≠y2 ), 怎样求出通过这两
点的直线方程呢?
x
y
P1(x1,y1)
P2(x2,y2)
两点式方程
一、直线的两点式方程
注意点:
(1)当经过两点(x1,y1),(x2,y2)的直线斜率不存在(x1=x2)或斜率为0(y1=y2)时,不能
用两点式方程表示.
经过两点P1(x1,y1),P2(x2,y2)(其中x1≠x2,y1≠y2)的直线方程 ,
我们把它叫做直线的两点式方程,简称:两点式.
一、直线的两点式方程
(2)两点式方程与这两个点的顺序无关.
(3)方程中等号两边表达式中分子之比等于分母之比,也就是同一条直线的斜率相等.
B(3,-3)
x
y
A(-5,0)
C(0,2)
例1: 已知三角形的三个顶点是A(-5,0),B(3,-3),C(0,2),求BC边所在的直线方程,以及该边上中线的直线
方程。
解:过B(3,-3),C(0,2)两点式方程为:
整理得:5x+3y-6=0
所以BC边所在直线的方程为:5x+3y-6=0
整理得:x+13y+5=0
所以BC边上中线所在直线的方程为:x+13y+5=0
一、直线的两点式方程
B(3,-3)
x
y
A(-5,0)
C(0,2)
例2: 已知三角形的三个顶点是A(-5,0),B(3,-3),C(0,2),求BC边垂直平分线的直线方程.
解:因为B(3,-3),C(0,2),
整理得:3x-5y-7=0
所以BC边的垂直平分线的方程为:3x-5y-7=0
一、直线的两点式方程
【练1】(1)过点A(-2,1),B(3,-3)的直线方程为_____________.
(2)已知直线经过点A(1,0),B(m,1),求这条直线的方程.
解(1)因为直线过点(-2,1)和(3,-3),
4x+5y+3=0
化简得:4x+5y+3=0.
一、直线的两点式方程
(2)由直线经过点A(1,0),B(m,1),因此该直线斜率不可能为零,但有可能不存在.
①当直线斜率不存在,即m=1时,直线方程为x=1;
②当直线斜率存在,即m≠1时,
即x-(m-1)y-1=0.
综上可得,当m=1时,直线方程为x=1;当m≠1时,直线方程为x-(m-1)y-1=0.
思考:两点式 适用所有直线吗?
适用范围:斜率存在,且不为0
平行于x轴,即y1= y2,方程为: y= y1
一、直线的两点式方程
平行于y轴,即x1 =x2,方程为:x =x1
思考 若给定直线上两点A(a,0),B(0,b)(a≠0,b≠0),
你能否得出直线的方程呢?
一、直线的两点式方程
x
l
B(0,b)
A(a,0)
O
y
解:将两点A(a,0), B(0,b)的坐标代入两点式,得:
即:
问题2:已知直线l与x轴的交点为A(a,0),与y轴的交点为B(0,b),其中a≠0,b≠0,用两点式
求这条直线l的方程.
x
l
B(0,b)
A(a,0)
O
y
一、直线的两点式方程
直线的截距式方程
二、直线的截距式方程
a为直线在x轴上的截距
b为直线在y轴上的截距
A(a,0)
x
l
B(0,b)
y
O
适用范围:斜率存在,且不为0,不经过原点
二、直线的截距式方程
直线与x轴的交点(a,0)的横坐标a叫做直线在x轴上的截距
思考:截距式与两点式有什么联系和区别?
区别:两点式:已知直线上两
点的坐标,写出的直线方程。
截距式:已知直线在两个坐标轴上的截距,
写出的直线方程。
联系:截距式方程是两点式方程
的特殊情况。
要求条件:斜率存在
且斜率不为0的直线。
要求条件:斜率存在且斜率不为0,还得不过原点的直线。
二、直线的截距式方程
注意点:
二、直线的截距式方程
(1)如果已知直线在两坐标轴上的截距,可以直接代入截距式求直线的方程.
(2)将直线的方程化为截距式后,可以观察出直线在x轴和y轴上的截距,这
一点常被用来作图.
(3)与坐标轴平行和过原点的直线都不能用截距式表示.
(4)过原点的直线的横、纵截距都为零.
解得a=-1.
即x-y+1=0.
二、直线的截距式方程
例3 求过点A(3,4),且在两坐标轴上的截距互为相反数的直线l的方程.
(2)当直线l在两坐标轴上的截距互为相反数且为0时,即直线l过原点时,设直线l的方程为y=kx,
因为l过点(3,4),所以4=k·3,
即4x-3y=0.
综上,直线l的方程为x-y+1=0或4x-3y=0.
【悟】 截距式方程应用的注意点
二、直线的截距式方程
(1)如果问题中涉及直线与坐标轴相交,则可考虑选用截距式方程,用待定系数法确定其系数即可.
(2)选用截距式方程时,必须首先考虑直线能否过原点以及能否与两坐标轴垂直.
(3)要注意截距式方程的逆向应用.
两边平方整理得:ab-12(a+b)+72=0. ①
所以直线l的方程为3x+4y-12=0或15x+8y-36=0.
二、直线的截距式方程
巩固练习
1:求满足下列条件的直线方程:
(1)经过点A(-3,-3),斜率是4;
(2)斜率是3,在y轴上的截距是-3;
(3)斜率是-3,在x轴上的截距是3;
(4)过点A(5,6)和点B(-1,2);
(5)在x轴和y轴上的截距分别为-2,3.
巩固练习
2、直线L与两直线y=1,x-y-7=0分别交于P,Q两点,线段PQ的中点是(1,-1),则L的斜率是____.
巩固练习
3、已知点A(m-1,m+1)与点B(m,m)关于直线l对称,则直线l的方程是 ( )
A.x+y-1=0 B.x-y+1=0 C.x+y+1=0 D.x-y-1=0
1.知识点:
课堂小结
2.方法:分类讨论法、数形结合法.
3.易错点:利用截距式求直线方程时忽略过原点的情况导致漏解.
一、直线方程的点斜式、斜截式?
温故知新
二、求直线方程的要点:
温故知新
三、求直线方程的注意点:
温故知新
【探究】我们知道已知两点也可以确定一条直线,在平面直角坐标系中,
给定一个点P0(x0,y0)和斜率k,可得出直线方程.若给定直线上
两点P1(x1,y1),P2(x2,y2)(x1≠x2,y1≠y2),能否得出直线的
方程呢?
温故知新
一、直线的两点式方程
问题1.已知直线上两点P1(x1,y1), P2(x2,y2)(其中x1≠x2,y1≠y2 ), 怎样求出通过这两
点的直线方程呢?
x
y
P1(x1,y1)
P2(x2,y2)
两点式方程
一、直线的两点式方程
注意点:
(1)当经过两点(x1,y1),(x2,y2)的直线斜率不存在(x1=x2)或斜率为0(y1=y2)时,不能
用两点式方程表示.
经过两点P1(x1,y1),P2(x2,y2)(其中x1≠x2,y1≠y2)的直线方程 ,
我们把它叫做直线的两点式方程,简称:两点式.
一、直线的两点式方程
(2)两点式方程与这两个点的顺序无关.
(3)方程中等号两边表达式中分子之比等于分母之比,也就是同一条直线的斜率相等.
B(3,-3)
x
y
A(-5,0)
C(0,2)
例1: 已知三角形的三个顶点是A(-5,0),B(3,-3),C(0,2),求BC边所在的直线方程,以及该边上中线的直线
方程。
解:过B(3,-3),C(0,2)两点式方程为:
整理得:5x+3y-6=0
所以BC边所在直线的方程为:5x+3y-6=0
整理得:x+13y+5=0
所以BC边上中线所在直线的方程为:x+13y+5=0
一、直线的两点式方程
B(3,-3)
x
y
A(-5,0)
C(0,2)
例2: 已知三角形的三个顶点是A(-5,0),B(3,-3),C(0,2),求BC边垂直平分线的直线方程.
解:因为B(3,-3),C(0,2),
整理得:3x-5y-7=0
所以BC边的垂直平分线的方程为:3x-5y-7=0
一、直线的两点式方程
【练1】(1)过点A(-2,1),B(3,-3)的直线方程为_____________.
(2)已知直线经过点A(1,0),B(m,1),求这条直线的方程.
解(1)因为直线过点(-2,1)和(3,-3),
4x+5y+3=0
化简得:4x+5y+3=0.
一、直线的两点式方程
(2)由直线经过点A(1,0),B(m,1),因此该直线斜率不可能为零,但有可能不存在.
①当直线斜率不存在,即m=1时,直线方程为x=1;
②当直线斜率存在,即m≠1时,
即x-(m-1)y-1=0.
综上可得,当m=1时,直线方程为x=1;当m≠1时,直线方程为x-(m-1)y-1=0.
思考:两点式 适用所有直线吗?
适用范围:斜率存在,且不为0
平行于x轴,即y1= y2,方程为: y= y1
一、直线的两点式方程
平行于y轴,即x1 =x2,方程为:x =x1
思考 若给定直线上两点A(a,0),B(0,b)(a≠0,b≠0),
你能否得出直线的方程呢?
一、直线的两点式方程
x
l
B(0,b)
A(a,0)
O
y
解:将两点A(a,0), B(0,b)的坐标代入两点式,得:
即:
问题2:已知直线l与x轴的交点为A(a,0),与y轴的交点为B(0,b),其中a≠0,b≠0,用两点式
求这条直线l的方程.
x
l
B(0,b)
A(a,0)
O
y
一、直线的两点式方程
直线的截距式方程
二、直线的截距式方程
a为直线在x轴上的截距
b为直线在y轴上的截距
A(a,0)
x
l
B(0,b)
y
O
适用范围:斜率存在,且不为0,不经过原点
二、直线的截距式方程
直线与x轴的交点(a,0)的横坐标a叫做直线在x轴上的截距
思考:截距式与两点式有什么联系和区别?
区别:两点式:已知直线上两
点的坐标,写出的直线方程。
截距式:已知直线在两个坐标轴上的截距,
写出的直线方程。
联系:截距式方程是两点式方程
的特殊情况。
要求条件:斜率存在
且斜率不为0的直线。
要求条件:斜率存在且斜率不为0,还得不过原点的直线。
二、直线的截距式方程
注意点:
二、直线的截距式方程
(1)如果已知直线在两坐标轴上的截距,可以直接代入截距式求直线的方程.
(2)将直线的方程化为截距式后,可以观察出直线在x轴和y轴上的截距,这
一点常被用来作图.
(3)与坐标轴平行和过原点的直线都不能用截距式表示.
(4)过原点的直线的横、纵截距都为零.
解得a=-1.
即x-y+1=0.
二、直线的截距式方程
例3 求过点A(3,4),且在两坐标轴上的截距互为相反数的直线l的方程.
(2)当直线l在两坐标轴上的截距互为相反数且为0时,即直线l过原点时,设直线l的方程为y=kx,
因为l过点(3,4),所以4=k·3,
即4x-3y=0.
综上,直线l的方程为x-y+1=0或4x-3y=0.
【悟】 截距式方程应用的注意点
二、直线的截距式方程
(1)如果问题中涉及直线与坐标轴相交,则可考虑选用截距式方程,用待定系数法确定其系数即可.
(2)选用截距式方程时,必须首先考虑直线能否过原点以及能否与两坐标轴垂直.
(3)要注意截距式方程的逆向应用.
两边平方整理得:ab-12(a+b)+72=0. ①
所以直线l的方程为3x+4y-12=0或15x+8y-36=0.
二、直线的截距式方程
巩固练习
1:求满足下列条件的直线方程:
(1)经过点A(-3,-3),斜率是4;
(2)斜率是3,在y轴上的截距是-3;
(3)斜率是-3,在x轴上的截距是3;
(4)过点A(5,6)和点B(-1,2);
(5)在x轴和y轴上的截距分别为-2,3.
巩固练习
2、直线L与两直线y=1,x-y-7=0分别交于P,Q两点,线段PQ的中点是(1,-1),则L的斜率是____.
巩固练习
3、已知点A(m-1,m+1)与点B(m,m)关于直线l对称,则直线l的方程是 ( )
A.x+y-1=0 B.x-y+1=0 C.x+y+1=0 D.x-y-1=0
1.知识点:
课堂小结
2.方法:分类讨论法、数形结合法.
3.易错点:利用截距式求直线方程时忽略过原点的情况导致漏解.
