青岛版(2015)六上-第五单元 1.圆及其性质【优质课件】
文档属性
| 名称 | 青岛版(2015)六上-第五单元 1.圆及其性质【优质课件】 |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-15 00:00:00 | ||
图片预览





文档简介
(共28张PPT)
圆的认识
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
01
课前导入
情景导入
根据这些信息,你能提出什么问题?
轮子为什么设计成圆形的呢?
02
新课精讲
探索新知
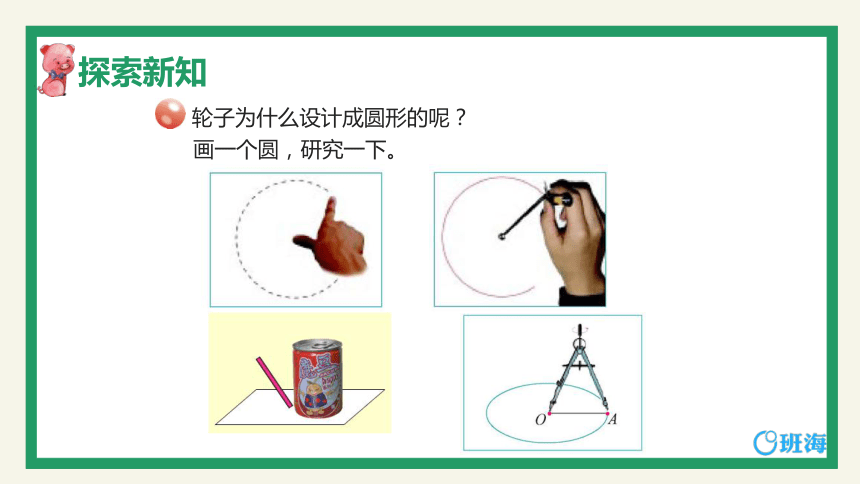
轮子为什么设计成圆形的呢?
画一个圆,研究一下。
探索新知
·
O
圆心
半径r
直径 d
·
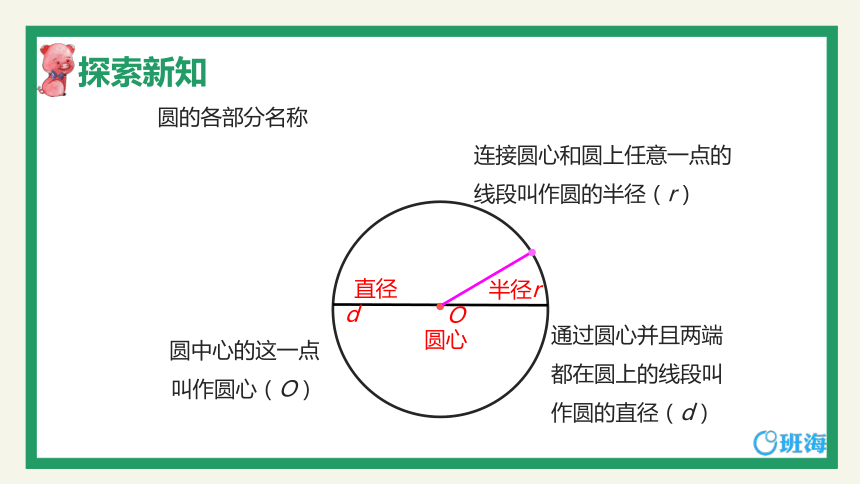
圆中心的这一点
叫作圆心(O)
连接圆心和圆上任意一点的
线段叫作圆的半径(r)
通过圆心并且两端都在圆上的线段叫作圆的直径(d)
圆的各部分名称
探索新知
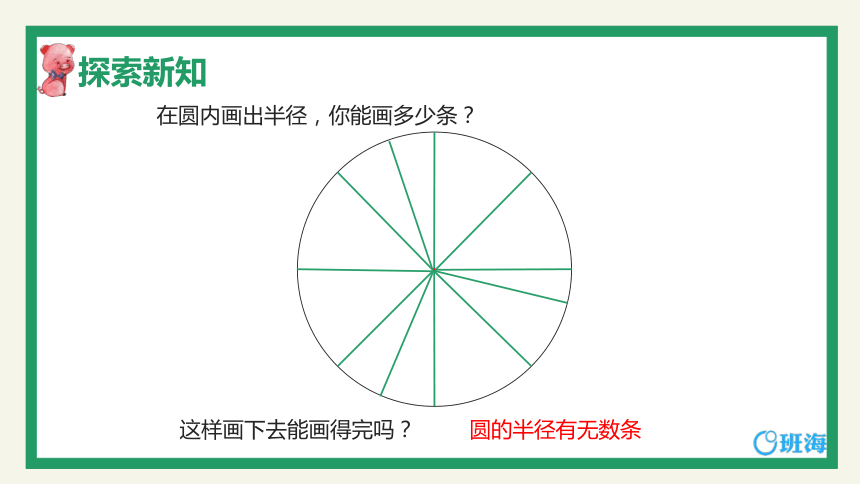
这样画下去能画得完吗?
圆的半径有无数条
在圆内画出半径,你能画多少条?
探索新知
0
1
2
3
4
6
7
8
5
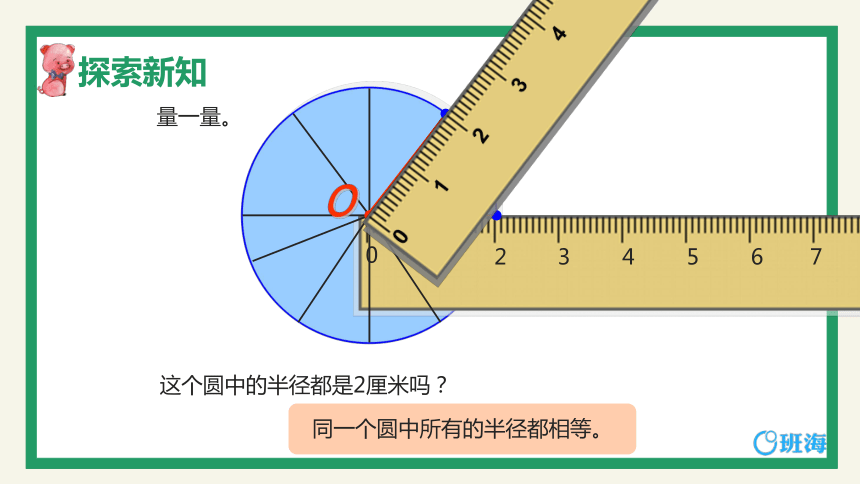
同一个圆中所有的半径都相等。
量一量。
这个圆中的半径都是2厘米吗?
探索新知
o
同一个圆内,直径有无数条,长度都相等。
在同一个圆里,有多少条直径?它们的长度有否变化?
探索新知
d=2r
r= d
2
半径与直径有什么关系呢?
r=2厘米
d=4厘米
探索新知
圆的特征
上面的这些图形是不是“一中同长”的图形?
探索新知
圆的特征
随着正多形边数的逐步增多,你发现了什么?
探索新知
圆的特征
椭圆同圆形一样也是由曲线围成的图形,它“一中同长”吗?
探索新知
下面图形中的涂色部分是什么图形?
O
O
O
O
跟扇子的形状差不多,都是由两条半径和一段曲线围成的。
这些图形都是圆面的一部分,并且都有一个顶点在圆心的角。
上面各圆中,涂色部分就是扇形。
探索新知
下面图形中的涂色部分是什么图形?
O
1
半径
半径
弧
A
B
圆心角
在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。
在右图中,圆中心的一点叫
作( ),用字母( )表示,
它到圆上任意一点的距离是圆
的( ),用字母( )表
示,直径用字母( )表示。
在同一个圆中,所有的半径都( ),所有的直径都( ),直径是半径的( ),半径与直径的比是( )。
典题精讲
圆心
O
半径
r
d
相等
相等
2倍
1∶2
d
O
r
典题精讲
2. 圆是( )图形,所有圆的( )所在的直线都是它的对称轴;圆有( )条对称轴。
3. 填表。
4. ( )决定圆的位置,( )决定圆的大小。
5. 圆规两脚间的距离是2.5厘米,这样画出的圆的直径是( )厘米。
轴对称
直径
无数
4
0.4
2.8
3
10
圆心
半径
5
典题精讲
6.扇形是由( )围成的。顶点在圆心的角叫作( )。扇形有( )条对称轴。
1
两条半径和一段曲线
圆心角
7.在下面的圆中各画出一个扇形并涂色。
略
易错提醒
判断。
(1)直径是半径的2倍。 ( )
(2)两端都在圆上的线段叫作直径。 ( )
×
×
辨析:对直径、半径的意义理解不准确。
03
学以致用
小试牛刀
1.火眼金睛辨对错。
(1)直径都是半径的2倍。 ( )
(2)等圆的半径都相等。 ( )
(3)两端都在圆上的线段叫做直径。 ( )
(4)两个圆的直径相等,半径也相等。 ( )
(5)圆内最长的线段是直径。( )
×
×
√
√
√
小试牛刀
0.24米
6米
直径(d)
3.9米
7厘米
20厘米
半径(r)
40厘米
3米
14厘米
0.12米
7.8米
2.填空。
小试牛刀
3.轮子为什么设计成圆形的呢?车轮设计成圆形的,车轴应安装在什么地方?
因为圆有无数条半径且长度都相等,便于车子平稳地行驶,同时圆具有易滚动的特点,所以车轮都设计成圆形的。
04
课堂小结
归纳总结:
1.把装有针尖的一只脚固定在纸上的一个点,然后以规定的长度绕固定点旋转一周,就画出一个圆。圆是有曲线围成的封闭图形。
2.画圆时,固定的点是圆心,圆心一般用字母O表示。连接圆心和圆上任意一点的线段叫做半径,一般用字母r表示。通过圆心并且两端都在圆上的线段叫直径,一般用字母d 表示。
3.圆心决定圆的位置,半径决定圆的大小。
4.圆是轴对称图形,直径所在的直线是圆的对称轴。圆有无数条对称轴。
5.在同圆或等圆中,所有的半径都相等,所有的直径都相等,r=d 或d=2r。
归纳总结:
1.圆上任意两点之间的部分叫作弧。
2.一条弧和经过这条弧两端的两条半径所围成的图形叫作扇形。
3.顶点在圆心的角就叫圆心角。在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。
同学们,下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
圆的认识
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
01
课前导入
情景导入
根据这些信息,你能提出什么问题?
轮子为什么设计成圆形的呢?
02
新课精讲
探索新知
轮子为什么设计成圆形的呢?
画一个圆,研究一下。
探索新知
·
O
圆心
半径r
直径 d
·
圆中心的这一点
叫作圆心(O)
连接圆心和圆上任意一点的
线段叫作圆的半径(r)
通过圆心并且两端都在圆上的线段叫作圆的直径(d)
圆的各部分名称
探索新知
这样画下去能画得完吗?
圆的半径有无数条
在圆内画出半径,你能画多少条?
探索新知
0
1
2
3
4
6
7
8
5
同一个圆中所有的半径都相等。
量一量。
这个圆中的半径都是2厘米吗?
探索新知
o
同一个圆内,直径有无数条,长度都相等。
在同一个圆里,有多少条直径?它们的长度有否变化?
探索新知
d=2r
r= d
2
半径与直径有什么关系呢?
r=2厘米
d=4厘米
探索新知
圆的特征
上面的这些图形是不是“一中同长”的图形?
探索新知
圆的特征
随着正多形边数的逐步增多,你发现了什么?
探索新知
圆的特征
椭圆同圆形一样也是由曲线围成的图形,它“一中同长”吗?
探索新知
下面图形中的涂色部分是什么图形?
O
O
O
O
跟扇子的形状差不多,都是由两条半径和一段曲线围成的。
这些图形都是圆面的一部分,并且都有一个顶点在圆心的角。
上面各圆中,涂色部分就是扇形。
探索新知
下面图形中的涂色部分是什么图形?
O
1
半径
半径
弧
A
B
圆心角
在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。
在右图中,圆中心的一点叫
作( ),用字母( )表示,
它到圆上任意一点的距离是圆
的( ),用字母( )表
示,直径用字母( )表示。
在同一个圆中,所有的半径都( ),所有的直径都( ),直径是半径的( ),半径与直径的比是( )。
典题精讲
圆心
O
半径
r
d
相等
相等
2倍
1∶2
d
O
r
典题精讲
2. 圆是( )图形,所有圆的( )所在的直线都是它的对称轴;圆有( )条对称轴。
3. 填表。
4. ( )决定圆的位置,( )决定圆的大小。
5. 圆规两脚间的距离是2.5厘米,这样画出的圆的直径是( )厘米。
轴对称
直径
无数
4
0.4
2.8
3
10
圆心
半径
5
典题精讲
6.扇形是由( )围成的。顶点在圆心的角叫作( )。扇形有( )条对称轴。
1
两条半径和一段曲线
圆心角
7.在下面的圆中各画出一个扇形并涂色。
略
易错提醒
判断。
(1)直径是半径的2倍。 ( )
(2)两端都在圆上的线段叫作直径。 ( )
×
×
辨析:对直径、半径的意义理解不准确。
03
学以致用
小试牛刀
1.火眼金睛辨对错。
(1)直径都是半径的2倍。 ( )
(2)等圆的半径都相等。 ( )
(3)两端都在圆上的线段叫做直径。 ( )
(4)两个圆的直径相等,半径也相等。 ( )
(5)圆内最长的线段是直径。( )
×
×
√
√
√
小试牛刀
0.24米
6米
直径(d)
3.9米
7厘米
20厘米
半径(r)
40厘米
3米
14厘米
0.12米
7.8米
2.填空。
小试牛刀
3.轮子为什么设计成圆形的呢?车轮设计成圆形的,车轴应安装在什么地方?
因为圆有无数条半径且长度都相等,便于车子平稳地行驶,同时圆具有易滚动的特点,所以车轮都设计成圆形的。
04
课堂小结
归纳总结:
1.把装有针尖的一只脚固定在纸上的一个点,然后以规定的长度绕固定点旋转一周,就画出一个圆。圆是有曲线围成的封闭图形。
2.画圆时,固定的点是圆心,圆心一般用字母O表示。连接圆心和圆上任意一点的线段叫做半径,一般用字母r表示。通过圆心并且两端都在圆上的线段叫直径,一般用字母d 表示。
3.圆心决定圆的位置,半径决定圆的大小。
4.圆是轴对称图形,直径所在的直线是圆的对称轴。圆有无数条对称轴。
5.在同圆或等圆中,所有的半径都相等,所有的直径都相等,r=d 或d=2r。
归纳总结:
1.圆上任意两点之间的部分叫作弧。
2.一条弧和经过这条弧两端的两条半径所围成的图形叫作扇形。
3.顶点在圆心的角就叫圆心角。在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。
同学们,下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
