青岛版(2015)六上-第四单元 4.比的基本性质【优质课件】
文档属性
| 名称 | 青岛版(2015)六上-第四单元 4.比的基本性质【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-15 15:25:24 | ||
图片预览








文档简介
(共28张PPT)
比的基本性质
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
1
2
课前导入
学以致用
新课精讲
3
课堂小结
4
01
课前导入
情景导入
我们刚刚认识了比,比与分数、除法之间有着怎样的关系呢?
商不变的规律:被除数和除数同时乘或除以一个相同的数(0除外),商不变。
分数的基本性质:分子和分母同时乘或除以一个相同的数(0除外),分数大小不变。
比
分数
除法
前项
比号
后项
比值
分子
被除数
除号
分数线
分母
除数
分数值
商
你还记得分数的基本性质和商不变的性质吗?
根据这些信息,你能提出什么问题?
比有怎样的性质呢?
02
新课精讲
探索新知
想一想,比有怎样的性质?
比的前项和后项同时乘或除以相同的数,比值不变
举几个比的例子,将比的前项和后项同时乘或除以相同的数,看看比值的变化情况。
结论:
猜想:
验证:
比的前项和后项同时乘或除以相同的 ,
比值不变。
(0除外)
同时
相同的
(0除外)
这是比的基本性质。
猜想:
验证:
结论:
?
(3×2)
= 0.6
∶
(5×2)
3∶5
= 0.6
(3×5)
= 0.6
∶
(5×5)
...
(18÷2)
= 0.75
∶
(24÷2)
18∶24
= 0.75
(18÷3)
= 0.75
∶
(24÷3)
...
应用:
根据比的基本性质,可以把比化成最简单的整数比。
最简单的整数比
探索新知
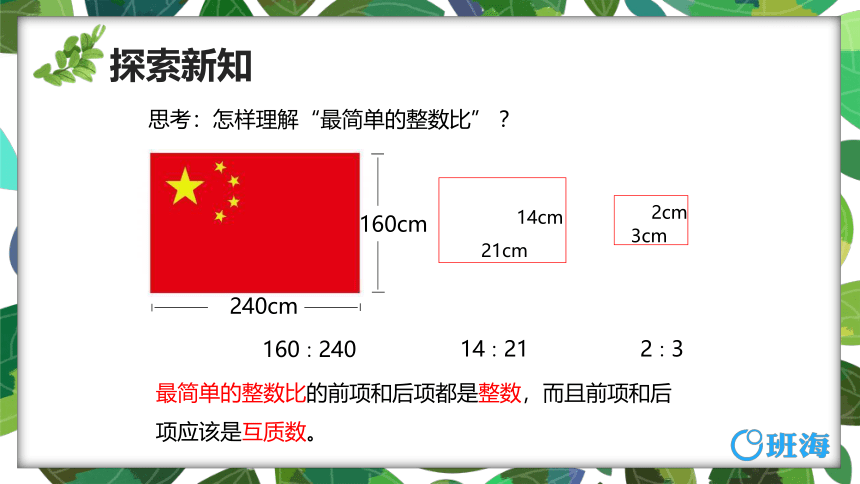
思考:怎样理解“最简单的整数比” ?
240cm
160cm
21cm
14cm
3cm
2cm
160∶240
14∶21
2∶3
最简单的整数比的前项和后项都是整数,而且前项和后项应该是互质数。
探索新知
14∶21 =(14÷7)∶(21÷7)= 2∶3
你能把14∶21、 ∶ 和1.25∶0.4化成最简单的整数比吗?
1
10
3
8
为什么同时除以7?
因为14和21的最大公因数是7。
∶ = ×40∶ ×40 =4∶15
1
10
3
8
1
10
3
8
因为10和8的最小公倍数40。
为什么同时乘40?
1.25∶0.4 =(1.25×100)∶(0.4×100)= 25∶8
为什么同时乘100?
因为1.25和0.4分别乘100,可以都转化成整数。
典题精讲
1. 想一想,填一填。
(1)比的前项和后项( )(0除外),比值不变,这叫作比的基本性质。
(2)5∶8=5÷( )= =
(3)如果a∶b= ,那么5a∶5b=( )。
(4)甲数与乙数的比是3∶5,如果甲乘 ,要使比值不变,乙数应当除以( )。
(5)如果a∶b= ,那么(a÷9)∶(b÷9)=( )。
同时乘或除以相同的数
8
10
8
10
典题精讲
(6)3∶4的前项扩大到原来的7倍,要使比值不变,后项应扩大到原来的( )倍。
(7)完成一份作业,小明要用10分钟,小强要用12分钟,小明与小强所用时间的比是( ),做作业效率的比是( )。
(8)一辆汽车3小时行驶135千米,汽车所行路程和时间的比是( ),比的前项和后项同时除以( )就是45∶1。
(9)一根绳子全长2.4米,用去0.6米,用去的和全长的比是( ),前项和后项同时乘( )可化成整数比( )。
7
10∶12
12∶10
135∶3
3
0.6∶2.4
5
3∶12
典题精讲
2. 快乐判断。(对的打“√”,错的打“×”)
(1)3∶4的前项加上6,要使比值不变,比的后项也应加上6。 ( )
(2)比的前项乘2,后项乘 ,比值扩大到原来的4倍。 ( )
(3)三角形的底与高的比是4∶3,说明三角形的底是3厘米,高是4厘米。 ( )
(4)5克盐溶解在50克水中,这时盐和盐水的质量比是1∶10。 ( )
×
√
×
×
(5)把“1时∶45分”化简后是“1∶45”。 ( )
×
典题精讲
24∶32=(24÷ )∶(32÷ )=( )∶( )
∶ = ( × )∶( × )
=( )∶( )
=( )∶( )
0.6∶2.4=(0.6× )∶(2.4× )
=( )∶( )
=( )∶( )
8
8
3
4
15
15
12
10
6
5
10
10
6
24
1
4
3. 想一想,算一算。
典题精讲
4. 化简下列各比。
典题精讲
5. 精挑细选。(将正确答案的序号填在括号里)
(1)如果a=2×3×5,b=2×3×3×7,那么a与b的最简整数比是( )。
A.30∶126 B.6∶18
C.5∶21 D.15∶63
(2)比的前项和后项都乘 ,比值( )。
A.不变 B.变大
C.变小 D.无法确定
C
A
典题精讲
(3)在8∶9中,如果前项增加16,要使比值不变,后项应( )。
A.增加16 B.乘3 C.不变 D.无法确定
(4)最简整数比的前项和后项一定是( )。
A.质数 B.合数 C.只有公因数1 D.奇数
B
C
(6)糖的质量占糖水的 ,糖与水的质量比是( )。
A.2∶7 B.2∶5 C.2∶9 D.5∶2
B
B
(5)化简比的理论依据是( )。
A.除法的意义 B.比的基本性质
C.加法的性质 D.除法的性质
易错提醒
下面的化简比对吗?若不对,请改正过来。
45∶9
=(45÷9)∶(9÷9)
=5
不对 45∶9=(45÷9)∶(9÷9) =5∶1
辨析:混淆化简比的结果与比值的表现形式。
03
学以致用
小试牛刀
1.把160∶240化成最简单的整数比。
160∶240
= (160÷80)
= 2∶3
160∶240
=
160
240
3
2
2
3
=
∶
(240÷80)
小试牛刀
2.化简下面各比。
1
2
∶
7
= 1∶14
∶
1
2
=
( × 2)
1
1
( 7 × 2 )
3∶0.25
∶
3
0
0
=
=(300÷25)
= 12∶1
∶
(25÷25)
0 25
.
小试牛刀
① 8∶10
= 4∶5
=(8÷2)
∶
(10÷2)
②0.72∶0.36
=(0.72÷0.36)
= 2∶1
∶
(0.36÷0.36)
3.化简下面各比。
= 5∶4
∶
=
5
6
( × 6)
1
1
2
3
5
6
∶
( × 6 )
2
3
1
2
1
25
25
1
=
100
4
100
4
=
④
③
小试牛刀
∶
4
5
=
( × 45)
9
1
8
9
4
5
∶
( × 45 )
8
9
1
5
0.3∶2
= 9∶10
=(36÷4)
∶
(40÷4)
= 3∶20
3.化简下面各比。
⑤
⑥
小试牛刀
4.(1)一台34英寸普通电视机屏幕的长为68厘米,宽为51厘米。写出长与宽的比,并化简。
(2)一台32英寸数字电视机屏幕的长为72厘米,宽为40.5厘米。写出长与宽的比,并化简。
68∶51
= 4∶3
∶
=(68÷17)
(51÷17)
72∶40.5
=
720
405
81
144
16
9
=
16
9
小试牛刀
5.人体每天需要的水分约为2500毫升,其中从食物中摄取的
约为1200毫升,直接饮入的约为1300毫升。写出从食物中
摄取的和直接饮入的水量的比,并化简。
1200∶1300
= (1200÷100)∶(1300÷100)
答:从食物中摄取的和直接饮入的水量的比是1200∶1300,化简后是12∶13。
= 12∶13
小试牛刀
铁 铜 金 银
体积(cm3) 5 10 4 6
质量(g) 39 89.2 77.2 63
质量与体积比的比值(g / cm3)
6.填一填。
7.8
8.92
19.3
10.5
小试牛刀
7. 根据求比值和化简比的方法填写表格。
1∶8
5∶21
4∶1
5∶1
16∶3
04
课堂小结
归纳总结:
化简比也不难,
分数比、小数比,先化整数再变简。
再把最大公因数除,保证得到最简比。
同学们,下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
比的基本性质
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
1
2
课前导入
学以致用
新课精讲
3
课堂小结
4
01
课前导入
情景导入
我们刚刚认识了比,比与分数、除法之间有着怎样的关系呢?
商不变的规律:被除数和除数同时乘或除以一个相同的数(0除外),商不变。
分数的基本性质:分子和分母同时乘或除以一个相同的数(0除外),分数大小不变。
比
分数
除法
前项
比号
后项
比值
分子
被除数
除号
分数线
分母
除数
分数值
商
你还记得分数的基本性质和商不变的性质吗?
根据这些信息,你能提出什么问题?
比有怎样的性质呢?
02
新课精讲
探索新知
想一想,比有怎样的性质?
比的前项和后项同时乘或除以相同的数,比值不变
举几个比的例子,将比的前项和后项同时乘或除以相同的数,看看比值的变化情况。
结论:
猜想:
验证:
比的前项和后项同时乘或除以相同的 ,
比值不变。
(0除外)
同时
相同的
(0除外)
这是比的基本性质。
猜想:
验证:
结论:
?
(3×2)
= 0.6
∶
(5×2)
3∶5
= 0.6
(3×5)
= 0.6
∶
(5×5)
...
(18÷2)
= 0.75
∶
(24÷2)
18∶24
= 0.75
(18÷3)
= 0.75
∶
(24÷3)
...
应用:
根据比的基本性质,可以把比化成最简单的整数比。
最简单的整数比
探索新知
思考:怎样理解“最简单的整数比” ?
240cm
160cm
21cm
14cm
3cm
2cm
160∶240
14∶21
2∶3
最简单的整数比的前项和后项都是整数,而且前项和后项应该是互质数。
探索新知
14∶21 =(14÷7)∶(21÷7)= 2∶3
你能把14∶21、 ∶ 和1.25∶0.4化成最简单的整数比吗?
1
10
3
8
为什么同时除以7?
因为14和21的最大公因数是7。
∶ = ×40∶ ×40 =4∶15
1
10
3
8
1
10
3
8
因为10和8的最小公倍数40。
为什么同时乘40?
1.25∶0.4 =(1.25×100)∶(0.4×100)= 25∶8
为什么同时乘100?
因为1.25和0.4分别乘100,可以都转化成整数。
典题精讲
1. 想一想,填一填。
(1)比的前项和后项( )(0除外),比值不变,这叫作比的基本性质。
(2)5∶8=5÷( )= =
(3)如果a∶b= ,那么5a∶5b=( )。
(4)甲数与乙数的比是3∶5,如果甲乘 ,要使比值不变,乙数应当除以( )。
(5)如果a∶b= ,那么(a÷9)∶(b÷9)=( )。
同时乘或除以相同的数
8
10
8
10
典题精讲
(6)3∶4的前项扩大到原来的7倍,要使比值不变,后项应扩大到原来的( )倍。
(7)完成一份作业,小明要用10分钟,小强要用12分钟,小明与小强所用时间的比是( ),做作业效率的比是( )。
(8)一辆汽车3小时行驶135千米,汽车所行路程和时间的比是( ),比的前项和后项同时除以( )就是45∶1。
(9)一根绳子全长2.4米,用去0.6米,用去的和全长的比是( ),前项和后项同时乘( )可化成整数比( )。
7
10∶12
12∶10
135∶3
3
0.6∶2.4
5
3∶12
典题精讲
2. 快乐判断。(对的打“√”,错的打“×”)
(1)3∶4的前项加上6,要使比值不变,比的后项也应加上6。 ( )
(2)比的前项乘2,后项乘 ,比值扩大到原来的4倍。 ( )
(3)三角形的底与高的比是4∶3,说明三角形的底是3厘米,高是4厘米。 ( )
(4)5克盐溶解在50克水中,这时盐和盐水的质量比是1∶10。 ( )
×
√
×
×
(5)把“1时∶45分”化简后是“1∶45”。 ( )
×
典题精讲
24∶32=(24÷ )∶(32÷ )=( )∶( )
∶ = ( × )∶( × )
=( )∶( )
=( )∶( )
0.6∶2.4=(0.6× )∶(2.4× )
=( )∶( )
=( )∶( )
8
8
3
4
15
15
12
10
6
5
10
10
6
24
1
4
3. 想一想,算一算。
典题精讲
4. 化简下列各比。
典题精讲
5. 精挑细选。(将正确答案的序号填在括号里)
(1)如果a=2×3×5,b=2×3×3×7,那么a与b的最简整数比是( )。
A.30∶126 B.6∶18
C.5∶21 D.15∶63
(2)比的前项和后项都乘 ,比值( )。
A.不变 B.变大
C.变小 D.无法确定
C
A
典题精讲
(3)在8∶9中,如果前项增加16,要使比值不变,后项应( )。
A.增加16 B.乘3 C.不变 D.无法确定
(4)最简整数比的前项和后项一定是( )。
A.质数 B.合数 C.只有公因数1 D.奇数
B
C
(6)糖的质量占糖水的 ,糖与水的质量比是( )。
A.2∶7 B.2∶5 C.2∶9 D.5∶2
B
B
(5)化简比的理论依据是( )。
A.除法的意义 B.比的基本性质
C.加法的性质 D.除法的性质
易错提醒
下面的化简比对吗?若不对,请改正过来。
45∶9
=(45÷9)∶(9÷9)
=5
不对 45∶9=(45÷9)∶(9÷9) =5∶1
辨析:混淆化简比的结果与比值的表现形式。
03
学以致用
小试牛刀
1.把160∶240化成最简单的整数比。
160∶240
= (160÷80)
= 2∶3
160∶240
=
160
240
3
2
2
3
=
∶
(240÷80)
小试牛刀
2.化简下面各比。
1
2
∶
7
= 1∶14
∶
1
2
=
( × 2)
1
1
( 7 × 2 )
3∶0.25
∶
3
0
0
=
=(300÷25)
= 12∶1
∶
(25÷25)
0 25
.
小试牛刀
① 8∶10
= 4∶5
=(8÷2)
∶
(10÷2)
②0.72∶0.36
=(0.72÷0.36)
= 2∶1
∶
(0.36÷0.36)
3.化简下面各比。
= 5∶4
∶
=
5
6
( × 6)
1
1
2
3
5
6
∶
( × 6 )
2
3
1
2
1
25
25
1
=
100
4
100
4
=
④
③
小试牛刀
∶
4
5
=
( × 45)
9
1
8
9
4
5
∶
( × 45 )
8
9
1
5
0.3∶2
= 9∶10
=(36÷4)
∶
(40÷4)
= 3∶20
3.化简下面各比。
⑤
⑥
小试牛刀
4.(1)一台34英寸普通电视机屏幕的长为68厘米,宽为51厘米。写出长与宽的比,并化简。
(2)一台32英寸数字电视机屏幕的长为72厘米,宽为40.5厘米。写出长与宽的比,并化简。
68∶51
= 4∶3
∶
=(68÷17)
(51÷17)
72∶40.5
=
720
405
81
144
16
9
=
16
9
小试牛刀
5.人体每天需要的水分约为2500毫升,其中从食物中摄取的
约为1200毫升,直接饮入的约为1300毫升。写出从食物中
摄取的和直接饮入的水量的比,并化简。
1200∶1300
= (1200÷100)∶(1300÷100)
答:从食物中摄取的和直接饮入的水量的比是1200∶1300,化简后是12∶13。
= 12∶13
小试牛刀
铁 铜 金 银
体积(cm3) 5 10 4 6
质量(g) 39 89.2 77.2 63
质量与体积比的比值(g / cm3)
6.填一填。
7.8
8.92
19.3
10.5
小试牛刀
7. 根据求比值和化简比的方法填写表格。
1∶8
5∶21
4∶1
5∶1
16∶3
04
课堂小结
归纳总结:
化简比也不难,
分数比、小数比,先化整数再变简。
再把最大公因数除,保证得到最简比。
同学们,下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
