五校联考2022-2023学年高二上学期收假收心考试数学试题(Word版含解析)
文档属性
| 名称 | 五校联考2022-2023学年高二上学期收假收心考试数学试题(Word版含解析) | 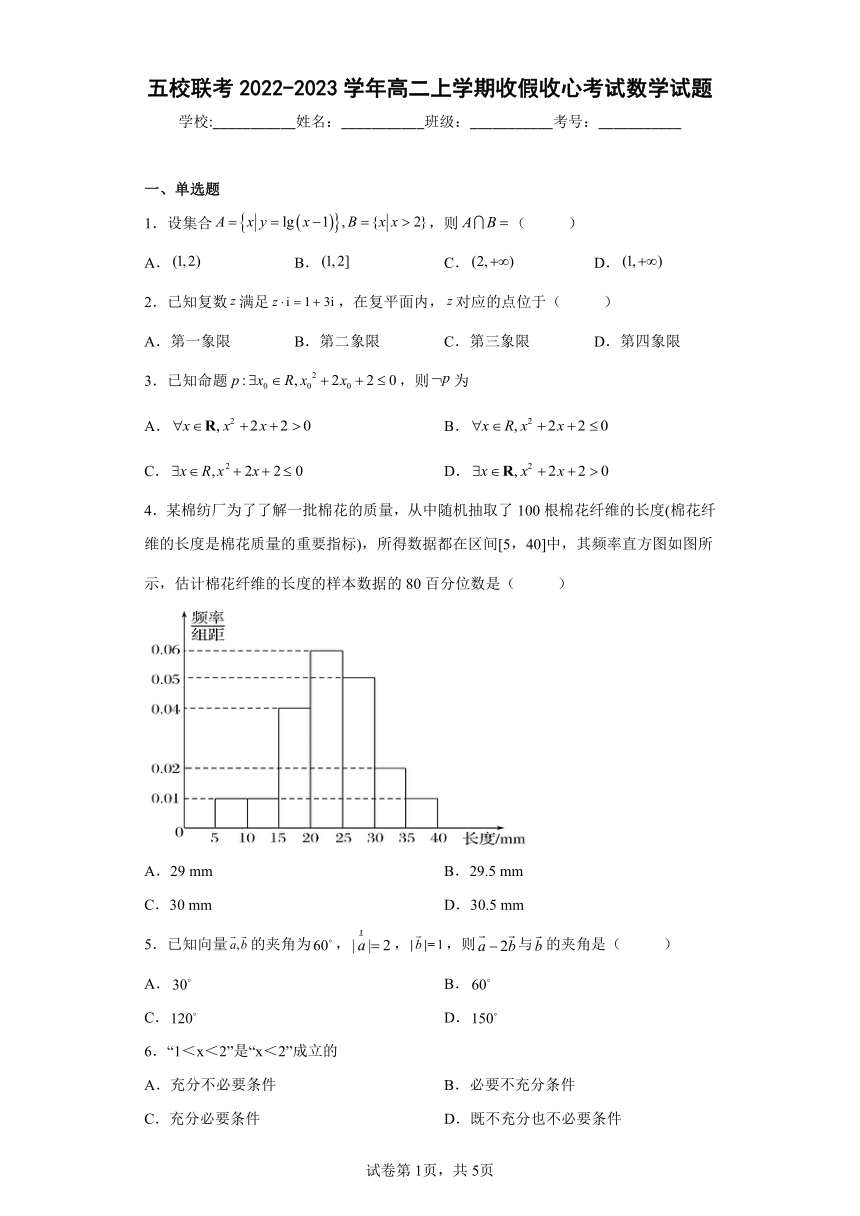 | |
| 格式 | zip | ||
| 文件大小 | 902.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-15 17:32:48 | ||
图片预览





文档简介
五校联考2022-2023学年高二上学期收假收心考试数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.设集合,则( )
A. B. C. D.
2.已知复数满足,在复平面内,对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知命题,则为
A. B.
C. D.
4.某棉纺厂为了了解一批棉花的质量,从中随机抽取了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标),所得数据都在区间[5,40]中,其频率直方图如图所示,估计棉花纤维的长度的样本数据的80百分位数是( )
A.29 mm B.29.5 mm
C.30 mm D.30.5 mm
5.已知向量的夹角为,,,则与的夹角是( )
A. B.
C. D.
6.“1<x<2”是“x<2”成立的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
7.如图,梯形是一平面图形的斜二侧直观图,若,,,则四边形的面积是( )
A.20 B.10 C. D.
8.为了得到函数的图象,只要将的图象上所有的点( )
A.向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变
B.向右平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
C.向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变
D.向右移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
9.若,,,则、、的大小关系是( )
A. B.
C. D.
10.在中,,则与的大小关系为
A. B. C. D.不确定
11.已知,是空间两条不同的直线,已知,是空间两个不同的平面,对于如下四个命题:
①若,,,则;②若,,,则;
③若,,,则;④若,,,则.
其中正确命题的序号是( )
A.①②③④ B.②③
C.①②④ D.①③④
12.已知,是空间中两个不同平面,,是空间中两条不同直线,则下列命题中错误的是
A.若,⊥,则⊥
B.若,,则
C.若⊥,⊥,则
D.若⊥,,则
二、填空题
13.为了研究疫情病毒和人的血型间的关系,在被感染的2400人中,O型血有800人,A型血有600人,B型血有600人,AB型血有400人.在这2400人中,采用分层抽样的方法抽取一个容量为120人的样本,则应从O型血中抽取的人数为_____.
14.从3名男生和名女生中,任选3人参加比赛,已知3人中至少有1名女生的概率为,则 _____.
15.中,点满足,若,则___________.
16.已知三棱锥的顶点都在以为直径的球M的球面上,,球M的表面积为,当三棱锥的体积最大时,点A到平面的距离为___________.
三、解答题
17.已知向量满足,且.
(1)求与的夹角;
(2)求.
18.栀子原产于中国,喜温暖湿润、阳光充足的环境,较耐寒.叶,四季常绿;花,芳香素雅.绿叶白花,格外清丽.某地区引种了一批栀子作为绿化景观植物,一段时间后,从该批栀子中随机抽取棵测量植株高度,并以此测量数据作为样本,得到该样本的频率分布直方图(单位:),其中不大于(单位:)的植株高度茎叶图如图所示.
(1)求植株高度频率分布直方图中的值;
(2)在植株高度频率分布直方图中,同一组中的数据用该区间的中点值代表,植株高度落入该区间的频率作为植株高度取该区间中点值的频率,估计这批栀子植株高度的平均值.
19.如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,E、F、G分别是棱AB、AP、PD的中点.
(1)证明:平面EFG;
(2)若,,求点C到平面EFG的距离.
20.已知,,,设函数.
(1)求函数的最小正周期T;
(2)若,求的值域
21.在①(b-c)cos A=acosC ,②sin(B+C)=-1+2sin2 , ③acosC=b-c ,这三个条件中任选一个作为已知条件,然后解答问题.
在△ABC 中,内角 A,B,C 的对边分别为 a,b,c,已知______________.
(1)求角 A 的大小;
(2)若 a=2 ,且△ ABC 的面积为 2,求 b+c .
22.已知定义域为的函数是奇函数,其中为指数函数且的图象过点.
(1)求的表达式;
(2)若对任意的.不等式恒成立,求实数的取值范围;
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】化简集合A,根据交集运算即可.
【详解】由题知,则,则,从而得到.
故选:C
2.D
【分析】根据复数的几何意义与四则运算法则计算.
【详解】由,得,
所以对应的点为,位于第四象限.
故选:D
3.A
【分析】根据特称命题的否定是全称命题得到答案.
【详解】特称命题的否定是全称命题,
命题,则为:.
故选:.
【点睛】本题考查了特称命题的否定,意在考查学生的推断能力.
4.A
【分析】先求得棉花纤维的长度在30 mm以下的比例为85%,在25 mm以下的比例为85%-25%=60%,从而可得80百分位数一定位于[25,30)内,进而可求出答案
【详解】棉花纤维的长度在30 mm以下的比例为(0.01+0.01+0.04+0.06+0.05)×5=0.85=85%,
在25 mm以下的比例为85%-25%=60%,
因此,80百分位数一定位于[25,30)内,
由,
可以估计棉花纤维的长度的样本数据的80百分位数是29 mm.
故选:A
5.C
【分析】根据数量积的定义求出,再根据数量积的运算律求出、,最后根据计算可得;
【详解】解:因为向量的夹角为,,,所以,∴,
∵,
∴,
∵
∴与的夹角是,
故选:C.
6.A
【详解】试题分析:因为“若,则”是真命题,“若,则”是假命题,所以“”是“”成立的充分不必要条件.选A.
考点:充分必要条件的判断.
【易错点睛】本题主要考查了充分条件,必要条件,充要条件的判断,属于基础题. 对于命题“若,则
”是真命题,我们说,并且说是的充分条件,是的必要条件,命题“若,则”是假命题,我们说,由充分条件,必要条件的定义,可以判断出“”是“”成立的充分不必要条件.掌握充分条件,必要条件的定义是解题关键.
7.B
【分析】根据斜二测画法画出原图,并计算出原图的面积.
【详解】根据直观图画法的规则,可得,且;
,且,
即梯形上底和下底边长分别为,高为,
如下图所示,故其面积.
故选:B
8.A
【分析】首先向左平移,可得,再横坐标缩小原来的倍,即可确定选项.
【详解】因为函数
将函数图象向左平移个单位后所得到的函数图象对应的解析式为,再把所得各点的横坐标缩短到原来的倍,
所得到的函数图象对应的解析式为.
故选:A.
9.D
【分析】利用指数函数、对数函数的单调性结合中间值法可得出、、的大小关系.
【详解】因为,,,
因此,.
故选:D.
10.C
【详解】分析:利用正弦定理,化角为边,再由大边对大角可得结果.
详解:在△ABC中,若sinA>sinB,由正弦定理可得:a>b,可得A>B.
故选C.
点睛:本题考查了正弦定理的简单应用,属于基础题.
11.D
【分析】由平行关系和垂直关系的相关定理依次判断各个选项可知①③④正确;由反例可知②错误.
【详解】对于①,,,,又,,①正确;
对于②,在如图所示的正方体中,
若,,平面,平面,
则满足,,,此时,②错误;
对于③,,,,又,则在中必存在直线,,
又,,③正确;
对于④,,,分别为的法向量,
又,与所成角为,即,④正确.
故选:D.
12.B
【详解】试题分析:若,,则与可能异面,故B错误,应选B.
考点:空间点线面位置关系.
13.40
【分析】直接根据其所占比例求解即可.
【详解】因为在被感染的2400人中,O型血有800人,A型血有600人,B型血有600人,AB型血有400人,即O型血的人数占,
所以应从O型血中抽取的人数为
故答案为:40
14.4
【分析】“3人中至少有1名女生”的对立事件是“3人中没有女生”,则3人没有女生的概率为 ,然后根据古典概型概率的计算公式即可得到答案
【详解】依题意在选出的3人中至少有1名女生的概率为,
其对立事件是“3人中没有女生”的概率为
依题意可得: ,解得
故答案为:4
15.
【分析】先由题设得,再由平面向量的线性运算及平面基本定理得出,即可求解.
【详解】
由可知,则,
则,则.
故答案为:.
16.4
【分析】证明面,,进而得到三棱锥的体积为,由和基本不等式
求出的最大值,求出体积最大时,利用等体积法即可求解.
【详解】如图,
因为三棱锥的顶点都在以PC为直径的球M的球面上,所以,又,,故面,
又 ,故面,又面,面,故,.
球M的表面积为,设球的半径为,则,解得,
即,所以,,
三棱锥的体积为,
要使体积最大,即最大,又,当且仅当时取等号,故体积的最大值为.
此时,设点A到平面的距离为,
则,解得.
故答案为:4
17.(1)
(2)
【分析】(1)根据数量积的定义和运算律即可求解夹角.
(2)根据模长公式即可求解.
(1)
由,
得,因为,所以.
(2)
由题意得
18.(1);(2)1.60.
【分析】(1)根据茎叶图可得频率,从而可计算.
(2)利用组中值可计算植株高度的平均值.
【详解】(1)由茎叶图知,.
由频率分布直方图知
,
所以.
(2)这批栀子植株高度的平均值的估计值
.
【点睛】本题考查频率的计算及频率分布直方图的应用,属于基础题.
19.(1)证明见解析
(2)
【分析】(1)依题意可得,,即可得到平面,再由为平行四边形得到,从而得到平面,即可得到平面平面,即可得证;
(2)取的中点,连接,,依题意可得,利用勾股定理逆定理可得,同理可得、,从而得到平面,平面,求出,,设到平面的距离为,由,利用等体积法求出,由为中点,即、到平面的距离相等,从而得解;
(1)
证明:因为E、F、G分别是棱AB、AP、PD的中点,
所以,,
又平面,平面,所以平面,
又因为底面为平行四边形,所以,则,
又平面,平面,所以平面,
因为,平面,所以平面平面,
又平面,所以平面,
(2)
解:取的中点,连接,,
则且,
所以,
因为,,所以,即,
同理可得、,
又,平面,所以平面,
,平面,所以平面,
所以平面,平面,所以,
因为,,
所以,,,
设到平面的距离为,又,
所以,则,
又因为为中点,所以、到平面的距离相等,
所以到平面的距离为;
20.(1);(2)
【分析】(1)利用数量积定义结合二倍角的正余弦公式化简f(x)为最简形式,再求周期;(2)利用整体换元法求函数的值域
【详解】(1)
故最小正周期
(2)若则 ,的值域为
21.(1)
(2)
【分析】(1)选①:化边为角化简求出cos;
选②:利用倍角公式将sin() = 1 + 2sin2化简为sin = cos,再利用辅助角公式求解即可;
选③:化边为角化简运算求解
(2)利用面积公式求得,再利用余弦定理可得,计算即可.
(1)
选①∵
∴sincos= sinCcos+ sincosC= sin(+ C) = sin
∴cos
∵ ∈ ,∴ =
选②∵sin() = 1 + 2sin2 ,∴sin = cos
∴sin( + A) = 1
∵A ∈∴A =
选③∵
∴
∴
∵A ∈ ,∴A =
(2)
∵ ,∴
又∵
∴ 即
22.(1);(2).
【分析】(1)设(且),因为的图象过点,求得a的值,再根据函数f(x)是奇函数,利用f(0)=0即可求得n的值,得到f(x)的解析式,检验是奇函数即可;
(2)将分式分离常数后,利用指数函数的性质可以判定f(x)在R上单调递减,进而结合奇函数的性质将不等式转化为二次不等式,根据二次函数的图象和性质,求得对于对任意的恒成立时a的取值范围即可.
【详解】解:(1)由题意,设(且),
因为的图象过点,可得,解得,即,
所以,
又因为为上的奇函数,
可得,即,解得,
经检验,符合,所以.
(2)由函数,可得在上单调递减,
又因为为奇函数,所以,
所以,即,
又因为对任意的,不等式恒成立,
令,即对任意的恒成立,
可得,即,解得,
所以实数的取值范围为.
【点睛】本题考查函数的奇偶性,指数函数及其性质和函数不等式恒成立问题,关键是利用函数的单调性和奇偶性将不等式转化为二次不等式在闭区间上恒成立问题,然后利用二次函数的图象转化为二次函数的端点值满足的条件.另外注意,第一问中,利用特值f(0)=0求得解析式后,要注意检验对于任意的实数x,f(x)=-f(-x)恒成立.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.设集合,则( )
A. B. C. D.
2.已知复数满足,在复平面内,对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知命题,则为
A. B.
C. D.
4.某棉纺厂为了了解一批棉花的质量,从中随机抽取了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标),所得数据都在区间[5,40]中,其频率直方图如图所示,估计棉花纤维的长度的样本数据的80百分位数是( )
A.29 mm B.29.5 mm
C.30 mm D.30.5 mm
5.已知向量的夹角为,,,则与的夹角是( )
A. B.
C. D.
6.“1<x<2”是“x<2”成立的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
7.如图,梯形是一平面图形的斜二侧直观图,若,,,则四边形的面积是( )
A.20 B.10 C. D.
8.为了得到函数的图象,只要将的图象上所有的点( )
A.向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变
B.向右平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
C.向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变
D.向右移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
9.若,,,则、、的大小关系是( )
A. B.
C. D.
10.在中,,则与的大小关系为
A. B. C. D.不确定
11.已知,是空间两条不同的直线,已知,是空间两个不同的平面,对于如下四个命题:
①若,,,则;②若,,,则;
③若,,,则;④若,,,则.
其中正确命题的序号是( )
A.①②③④ B.②③
C.①②④ D.①③④
12.已知,是空间中两个不同平面,,是空间中两条不同直线,则下列命题中错误的是
A.若,⊥,则⊥
B.若,,则
C.若⊥,⊥,则
D.若⊥,,则
二、填空题
13.为了研究疫情病毒和人的血型间的关系,在被感染的2400人中,O型血有800人,A型血有600人,B型血有600人,AB型血有400人.在这2400人中,采用分层抽样的方法抽取一个容量为120人的样本,则应从O型血中抽取的人数为_____.
14.从3名男生和名女生中,任选3人参加比赛,已知3人中至少有1名女生的概率为,则 _____.
15.中,点满足,若,则___________.
16.已知三棱锥的顶点都在以为直径的球M的球面上,,球M的表面积为,当三棱锥的体积最大时,点A到平面的距离为___________.
三、解答题
17.已知向量满足,且.
(1)求与的夹角;
(2)求.
18.栀子原产于中国,喜温暖湿润、阳光充足的环境,较耐寒.叶,四季常绿;花,芳香素雅.绿叶白花,格外清丽.某地区引种了一批栀子作为绿化景观植物,一段时间后,从该批栀子中随机抽取棵测量植株高度,并以此测量数据作为样本,得到该样本的频率分布直方图(单位:),其中不大于(单位:)的植株高度茎叶图如图所示.
(1)求植株高度频率分布直方图中的值;
(2)在植株高度频率分布直方图中,同一组中的数据用该区间的中点值代表,植株高度落入该区间的频率作为植株高度取该区间中点值的频率,估计这批栀子植株高度的平均值.
19.如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,E、F、G分别是棱AB、AP、PD的中点.
(1)证明:平面EFG;
(2)若,,求点C到平面EFG的距离.
20.已知,,,设函数.
(1)求函数的最小正周期T;
(2)若,求的值域
21.在①(b-c)cos A=acosC ,②sin(B+C)=-1+2sin2 , ③acosC=b-c ,这三个条件中任选一个作为已知条件,然后解答问题.
在△ABC 中,内角 A,B,C 的对边分别为 a,b,c,已知______________.
(1)求角 A 的大小;
(2)若 a=2 ,且△ ABC 的面积为 2,求 b+c .
22.已知定义域为的函数是奇函数,其中为指数函数且的图象过点.
(1)求的表达式;
(2)若对任意的.不等式恒成立,求实数的取值范围;
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】化简集合A,根据交集运算即可.
【详解】由题知,则,则,从而得到.
故选:C
2.D
【分析】根据复数的几何意义与四则运算法则计算.
【详解】由,得,
所以对应的点为,位于第四象限.
故选:D
3.A
【分析】根据特称命题的否定是全称命题得到答案.
【详解】特称命题的否定是全称命题,
命题,则为:.
故选:.
【点睛】本题考查了特称命题的否定,意在考查学生的推断能力.
4.A
【分析】先求得棉花纤维的长度在30 mm以下的比例为85%,在25 mm以下的比例为85%-25%=60%,从而可得80百分位数一定位于[25,30)内,进而可求出答案
【详解】棉花纤维的长度在30 mm以下的比例为(0.01+0.01+0.04+0.06+0.05)×5=0.85=85%,
在25 mm以下的比例为85%-25%=60%,
因此,80百分位数一定位于[25,30)内,
由,
可以估计棉花纤维的长度的样本数据的80百分位数是29 mm.
故选:A
5.C
【分析】根据数量积的定义求出,再根据数量积的运算律求出、,最后根据计算可得;
【详解】解:因为向量的夹角为,,,所以,∴,
∵,
∴,
∵
∴与的夹角是,
故选:C.
6.A
【详解】试题分析:因为“若,则”是真命题,“若,则”是假命题,所以“”是“”成立的充分不必要条件.选A.
考点:充分必要条件的判断.
【易错点睛】本题主要考查了充分条件,必要条件,充要条件的判断,属于基础题. 对于命题“若,则
”是真命题,我们说,并且说是的充分条件,是的必要条件,命题“若,则”是假命题,我们说,由充分条件,必要条件的定义,可以判断出“”是“”成立的充分不必要条件.掌握充分条件,必要条件的定义是解题关键.
7.B
【分析】根据斜二测画法画出原图,并计算出原图的面积.
【详解】根据直观图画法的规则,可得,且;
,且,
即梯形上底和下底边长分别为,高为,
如下图所示,故其面积.
故选:B
8.A
【分析】首先向左平移,可得,再横坐标缩小原来的倍,即可确定选项.
【详解】因为函数
将函数图象向左平移个单位后所得到的函数图象对应的解析式为,再把所得各点的横坐标缩短到原来的倍,
所得到的函数图象对应的解析式为.
故选:A.
9.D
【分析】利用指数函数、对数函数的单调性结合中间值法可得出、、的大小关系.
【详解】因为,,,
因此,.
故选:D.
10.C
【详解】分析:利用正弦定理,化角为边,再由大边对大角可得结果.
详解:在△ABC中,若sinA>sinB,由正弦定理可得:a>b,可得A>B.
故选C.
点睛:本题考查了正弦定理的简单应用,属于基础题.
11.D
【分析】由平行关系和垂直关系的相关定理依次判断各个选项可知①③④正确;由反例可知②错误.
【详解】对于①,,,,又,,①正确;
对于②,在如图所示的正方体中,
若,,平面,平面,
则满足,,,此时,②错误;
对于③,,,,又,则在中必存在直线,,
又,,③正确;
对于④,,,分别为的法向量,
又,与所成角为,即,④正确.
故选:D.
12.B
【详解】试题分析:若,,则与可能异面,故B错误,应选B.
考点:空间点线面位置关系.
13.40
【分析】直接根据其所占比例求解即可.
【详解】因为在被感染的2400人中,O型血有800人,A型血有600人,B型血有600人,AB型血有400人,即O型血的人数占,
所以应从O型血中抽取的人数为
故答案为:40
14.4
【分析】“3人中至少有1名女生”的对立事件是“3人中没有女生”,则3人没有女生的概率为 ,然后根据古典概型概率的计算公式即可得到答案
【详解】依题意在选出的3人中至少有1名女生的概率为,
其对立事件是“3人中没有女生”的概率为
依题意可得: ,解得
故答案为:4
15.
【分析】先由题设得,再由平面向量的线性运算及平面基本定理得出,即可求解.
【详解】
由可知,则,
则,则.
故答案为:.
16.4
【分析】证明面,,进而得到三棱锥的体积为,由和基本不等式
求出的最大值,求出体积最大时,利用等体积法即可求解.
【详解】如图,
因为三棱锥的顶点都在以PC为直径的球M的球面上,所以,又,,故面,
又 ,故面,又面,面,故,.
球M的表面积为,设球的半径为,则,解得,
即,所以,,
三棱锥的体积为,
要使体积最大,即最大,又,当且仅当时取等号,故体积的最大值为.
此时,设点A到平面的距离为,
则,解得.
故答案为:4
17.(1)
(2)
【分析】(1)根据数量积的定义和运算律即可求解夹角.
(2)根据模长公式即可求解.
(1)
由,
得,因为,所以.
(2)
由题意得
18.(1);(2)1.60.
【分析】(1)根据茎叶图可得频率,从而可计算.
(2)利用组中值可计算植株高度的平均值.
【详解】(1)由茎叶图知,.
由频率分布直方图知
,
所以.
(2)这批栀子植株高度的平均值的估计值
.
【点睛】本题考查频率的计算及频率分布直方图的应用,属于基础题.
19.(1)证明见解析
(2)
【分析】(1)依题意可得,,即可得到平面,再由为平行四边形得到,从而得到平面,即可得到平面平面,即可得证;
(2)取的中点,连接,,依题意可得,利用勾股定理逆定理可得,同理可得、,从而得到平面,平面,求出,,设到平面的距离为,由,利用等体积法求出,由为中点,即、到平面的距离相等,从而得解;
(1)
证明:因为E、F、G分别是棱AB、AP、PD的中点,
所以,,
又平面,平面,所以平面,
又因为底面为平行四边形,所以,则,
又平面,平面,所以平面,
因为,平面,所以平面平面,
又平面,所以平面,
(2)
解:取的中点,连接,,
则且,
所以,
因为,,所以,即,
同理可得、,
又,平面,所以平面,
,平面,所以平面,
所以平面,平面,所以,
因为,,
所以,,,
设到平面的距离为,又,
所以,则,
又因为为中点,所以、到平面的距离相等,
所以到平面的距离为;
20.(1);(2)
【分析】(1)利用数量积定义结合二倍角的正余弦公式化简f(x)为最简形式,再求周期;(2)利用整体换元法求函数的值域
【详解】(1)
故最小正周期
(2)若则 ,的值域为
21.(1)
(2)
【分析】(1)选①:化边为角化简求出cos;
选②:利用倍角公式将sin() = 1 + 2sin2化简为sin = cos,再利用辅助角公式求解即可;
选③:化边为角化简运算求解
(2)利用面积公式求得,再利用余弦定理可得,计算即可.
(1)
选①∵
∴sincos= sinCcos+ sincosC= sin(+ C) = sin
∴cos
∵ ∈ ,∴ =
选②∵sin() = 1 + 2sin2 ,∴sin = cos
∴sin( + A) = 1
∵A ∈∴A =
选③∵
∴
∴
∵A ∈ ,∴A =
(2)
∵ ,∴
又∵
∴ 即
22.(1);(2).
【分析】(1)设(且),因为的图象过点,求得a的值,再根据函数f(x)是奇函数,利用f(0)=0即可求得n的值,得到f(x)的解析式,检验是奇函数即可;
(2)将分式分离常数后,利用指数函数的性质可以判定f(x)在R上单调递减,进而结合奇函数的性质将不等式转化为二次不等式,根据二次函数的图象和性质,求得对于对任意的恒成立时a的取值范围即可.
【详解】解:(1)由题意,设(且),
因为的图象过点,可得,解得,即,
所以,
又因为为上的奇函数,
可得,即,解得,
经检验,符合,所以.
(2)由函数,可得在上单调递减,
又因为为奇函数,所以,
所以,即,
又因为对任意的,不等式恒成立,
令,即对任意的恒成立,
可得,即,解得,
所以实数的取值范围为.
【点睛】本题考查函数的奇偶性,指数函数及其性质和函数不等式恒成立问题,关键是利用函数的单调性和奇偶性将不等式转化为二次不等式在闭区间上恒成立问题,然后利用二次函数的图象转化为二次函数的端点值满足的条件.另外注意,第一问中,利用特值f(0)=0求得解析式后,要注意检验对于任意的实数x,f(x)=-f(-x)恒成立.
答案第1页,共2页
答案第1页,共2页
同课章节目录
