1.2.3相反数 课件(共20张PPT)
文档属性
| 名称 | 1.2.3相反数 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 916.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-16 08:18:48 | ||
图片预览







文档简介
(共20张PPT)
1.2.3相反数
人教版 七年级上册
教学目标
教学目标:
1.借助数轴理解相反数的概念,并能求给定数的相反数;
2.了解一对相反数在数轴上的位置关系;
3.掌握双重符号的化简;
4.通过从数和形两个方面理解相反数,初步体会数形结合的思想方法.
重点:借助数轴理解相反数的意义,懂得数轴上表示相反数的两个点关于原点对称.
难点:会求有理数的相反数.
新知导入
活动1:观察下列一组数+1和-1,+2.5和-2.5,+4和-4,并把它们在数轴上表示出来.
思考:
1)上述各对数之间有什么特点?
2)请写出一组具有上述特点的数.
3)表示各对数的点在数轴上有什么位置关系?
新知导入
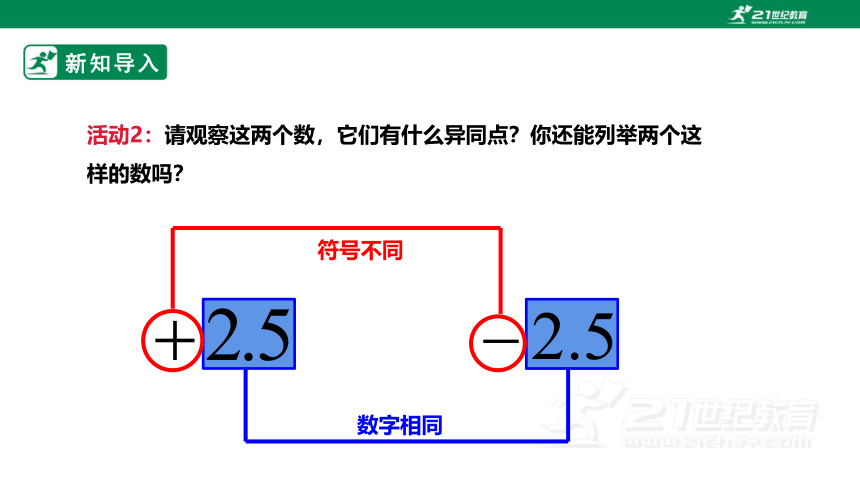
活动2:请观察这两个数,它们有什么异同点?你还能列举两个这样的数吗?
数字相同
符号不同
新知讲解
探究
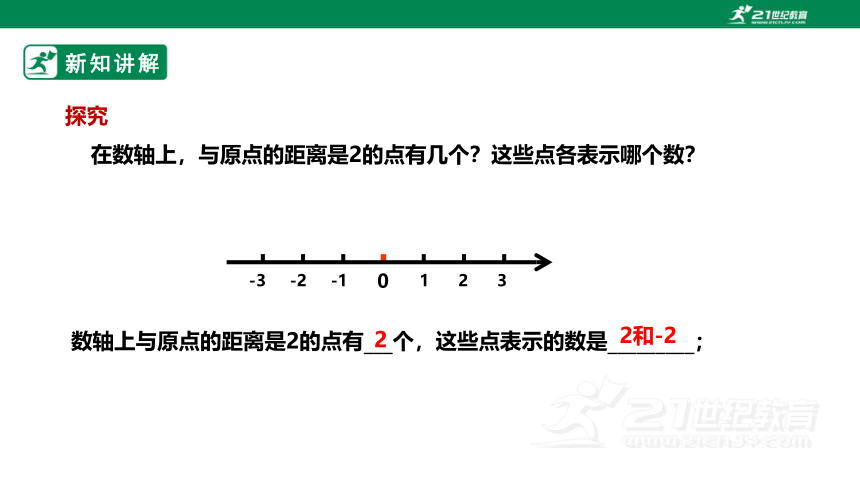
在数轴上,与原点的距离是2的点有几个?这些点各表示哪个数?
0
-3 -2 -1 1 2 3
数轴上与原点的距离是2的点有___个,这些点表示的数是_________;
2
2和-2
新知讲解
探究
设a是一个正数.数轴上与原点的距离等于a的点有几个?这些点表示的数有什么关系?
0
-a
a
-5
-2
2
5
一般地,设a是一个正数,数轴上与原点距离是a的点有两个,它们分别在原点左右,表示-a和a. 我们说这两点关于原点对称.
归纳
新知讲解
像-2和2,5和-5这样,只有符号不同的两个数叫做互为相反数。
注意:
1、通常a与-a互为相反数;
2、a表示任意一个数,可以是正数、负数,也可以是0;
3、特别注意,0的相反数是0.
相反数的概念
新知讲解
相反数的性质
任何一个数都有相反数,而且只有一个.
正数的相反数是负数;
0的相反数是0;
负数的相反数是正数.
0是唯一一个相反数等于它本身的数,即若a=-a,则a=0.
新知讲解
设a表示一个数,-a一定是负数吗?
1)若a为正数,则-a为负数;例:a=2,-a=-2
2)若a为0,则-a为0,即0的相反数就是其本身。
3)若a为负数,则-a为正数;例:a=-3,-a=-(-3)=?
0
正方向
1
2
3
-1
-2
-3
一般a和-a互为相反数,在数轴上-3到原点的距离为3,而原点的右侧也有一个点与原点的距离为3,所以-(-3)=3
新知讲解
例1 写出下列各数的相反数.
(1)7; (2)+6.3; (3)-;
(4)+[-]; (5)-[+3]; (6)-(-2.6)
解:(1)-7;(2)-(+6.3)=-6.3;(3)-[-]=;
(4)-{+[-]}=; (5)-{-[+3]}=;
(6)-[-(-2.6)]=-2.6
-(-28)=________; -(- )= ________.
新知讲解
-(-7)=______; +(-7)=________;
-(+0.68)=_______;-0=______;
例2 化简下列各数的符号:
7
-7
-0.68
0
28
-3
5
新知讲解
多重符号化简的依据
相反数的定义是多重符号化简的依据,
例如:-(-5)表示-5的相反数,所以(-5) =5.
多重符号的化简
先省略所有的“+”号,然后由“-”号的个数确定结果的符号.
当“-”号的个数是偶数时,化简的结果为正数;
当“-”号的个数是奇数时,化简的结果为负数.
2.数轴上表示互为相反数的两个点之间的距离为10,
则这两个数是 .
课堂练习
1.下面各组数,互为相反数的有 ( )组
; -(-8)与-(+8);
; -1.5 与 .
A.1 B.2 C.3 D.4
B
5和-5
课堂练习
C
3.一个数的相反数是非负数,那么这个数是( )
A.0 B.负数 C.非正数 D.正数
5.若两个数a、b互为相反数,则a+b= ;反过来, 若a+b=0,则a、b .
0
互为相反数
4.若a=-11,则-a=_______;若-a=-7,则a=______ .
11
7
课堂练习
6.化简下列各数
(1)-(+15) (2)+(-0.55) (3)+(+8)
(4)-(-19) (5)+[-(-4.1)] (6)-[+(-2)]
(6)-[+(-2)]=-(-2)=2.
解:(1)-(+15)=-15;
(2)+(-0.55)=-0.55;
(3)+(+8)=8;
(4)-(-19)=19;
(5)+[-(-4.1)]=+(+4.1)=4.1;
课堂练习
7.点A在数轴上,将点A先向左移动10个单位长度,再向右移动4个单位长度到点B,此时点B所表示的数与点A原来所表示的数互为相反数,求点A原来表示的数是多少
解:将点A先向左移动10个单位长度,再向右移动4个单位长度到点B,
相当于点A向左移动了6个单位长度,即AB的长度是6.
因为点A,B表示的数互为相反数,所以A,B两点与原点的距离都是3,所以点A表示的数是3.
课堂练习
8.已知a是-[-(-5)]的相反数,b比最小的正整数大4,c是相反数为它本身的数,计算3a+4b+5c的值.
解:因为-[-(-5)]=-5,所以a=-(-5)=5.
因为最小的正整数是1,b比最小的正整数大4,
所以b=1+4=5.
因为c是相反数为它本身的数,所以c=0.
所以3a+4b+5c=3×5+4×5+5×0=35.
课堂总结
相反数
相反数的代数意义
相反数的几何意义
相反数的表示方法
相反数的意义
相反数的应用—利用相反数化简双重符号
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.2.3相反数
人教版 七年级上册
教学目标
教学目标:
1.借助数轴理解相反数的概念,并能求给定数的相反数;
2.了解一对相反数在数轴上的位置关系;
3.掌握双重符号的化简;
4.通过从数和形两个方面理解相反数,初步体会数形结合的思想方法.
重点:借助数轴理解相反数的意义,懂得数轴上表示相反数的两个点关于原点对称.
难点:会求有理数的相反数.
新知导入
活动1:观察下列一组数+1和-1,+2.5和-2.5,+4和-4,并把它们在数轴上表示出来.
思考:
1)上述各对数之间有什么特点?
2)请写出一组具有上述特点的数.
3)表示各对数的点在数轴上有什么位置关系?
新知导入
活动2:请观察这两个数,它们有什么异同点?你还能列举两个这样的数吗?
数字相同
符号不同
新知讲解
探究
在数轴上,与原点的距离是2的点有几个?这些点各表示哪个数?
0
-3 -2 -1 1 2 3
数轴上与原点的距离是2的点有___个,这些点表示的数是_________;
2
2和-2
新知讲解
探究
设a是一个正数.数轴上与原点的距离等于a的点有几个?这些点表示的数有什么关系?
0
-a
a
-5
-2
2
5
一般地,设a是一个正数,数轴上与原点距离是a的点有两个,它们分别在原点左右,表示-a和a. 我们说这两点关于原点对称.
归纳
新知讲解
像-2和2,5和-5这样,只有符号不同的两个数叫做互为相反数。
注意:
1、通常a与-a互为相反数;
2、a表示任意一个数,可以是正数、负数,也可以是0;
3、特别注意,0的相反数是0.
相反数的概念
新知讲解
相反数的性质
任何一个数都有相反数,而且只有一个.
正数的相反数是负数;
0的相反数是0;
负数的相反数是正数.
0是唯一一个相反数等于它本身的数,即若a=-a,则a=0.
新知讲解
设a表示一个数,-a一定是负数吗?
1)若a为正数,则-a为负数;例:a=2,-a=-2
2)若a为0,则-a为0,即0的相反数就是其本身。
3)若a为负数,则-a为正数;例:a=-3,-a=-(-3)=?
0
正方向
1
2
3
-1
-2
-3
一般a和-a互为相反数,在数轴上-3到原点的距离为3,而原点的右侧也有一个点与原点的距离为3,所以-(-3)=3
新知讲解
例1 写出下列各数的相反数.
(1)7; (2)+6.3; (3)-;
(4)+[-]; (5)-[+3]; (6)-(-2.6)
解:(1)-7;(2)-(+6.3)=-6.3;(3)-[-]=;
(4)-{+[-]}=; (5)-{-[+3]}=;
(6)-[-(-2.6)]=-2.6
-(-28)=________; -(- )= ________.
新知讲解
-(-7)=______; +(-7)=________;
-(+0.68)=_______;-0=______;
例2 化简下列各数的符号:
7
-7
-0.68
0
28
-3
5
新知讲解
多重符号化简的依据
相反数的定义是多重符号化简的依据,
例如:-(-5)表示-5的相反数,所以(-5) =5.
多重符号的化简
先省略所有的“+”号,然后由“-”号的个数确定结果的符号.
当“-”号的个数是偶数时,化简的结果为正数;
当“-”号的个数是奇数时,化简的结果为负数.
2.数轴上表示互为相反数的两个点之间的距离为10,
则这两个数是 .
课堂练习
1.下面各组数,互为相反数的有 ( )组
; -(-8)与-(+8);
; -1.5 与 .
A.1 B.2 C.3 D.4
B
5和-5
课堂练习
C
3.一个数的相反数是非负数,那么这个数是( )
A.0 B.负数 C.非正数 D.正数
5.若两个数a、b互为相反数,则a+b= ;反过来, 若a+b=0,则a、b .
0
互为相反数
4.若a=-11,则-a=_______;若-a=-7,则a=______ .
11
7
课堂练习
6.化简下列各数
(1)-(+15) (2)+(-0.55) (3)+(+8)
(4)-(-19) (5)+[-(-4.1)] (6)-[+(-2)]
(6)-[+(-2)]=-(-2)=2.
解:(1)-(+15)=-15;
(2)+(-0.55)=-0.55;
(3)+(+8)=8;
(4)-(-19)=19;
(5)+[-(-4.1)]=+(+4.1)=4.1;
课堂练习
7.点A在数轴上,将点A先向左移动10个单位长度,再向右移动4个单位长度到点B,此时点B所表示的数与点A原来所表示的数互为相反数,求点A原来表示的数是多少
解:将点A先向左移动10个单位长度,再向右移动4个单位长度到点B,
相当于点A向左移动了6个单位长度,即AB的长度是6.
因为点A,B表示的数互为相反数,所以A,B两点与原点的距离都是3,所以点A表示的数是3.
课堂练习
8.已知a是-[-(-5)]的相反数,b比最小的正整数大4,c是相反数为它本身的数,计算3a+4b+5c的值.
解:因为-[-(-5)]=-5,所以a=-(-5)=5.
因为最小的正整数是1,b比最小的正整数大4,
所以b=1+4=5.
因为c是相反数为它本身的数,所以c=0.
所以3a+4b+5c=3×5+4×5+5×0=35.
课堂总结
相反数
相反数的代数意义
相反数的几何意义
相反数的表示方法
相反数的意义
相反数的应用—利用相反数化简双重符号
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
