22.3.2 实际问题与二次函数之利用二次函数解决投篮问题 学案(含答案)
文档属性
| 名称 | 22.3.2 实际问题与二次函数之利用二次函数解决投篮问题 学案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 177.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-15 18:00:43 | ||
图片预览

文档简介
实际问题与二次函数
-----利用二次函数解决投篮问题
知识链接
Hi,在开始挑战之前,先来热下身吧!
在实际问题中遇到最大(小)值问题时,往往先建立函数关系式,
如果是二次函数关系的,一般通过配方化为顶点式求解,也可以
用公式求解.
学习任务
(一)读教材,首战告捷
让我们一起来阅读教材,并做好色笔区分吧。
试身手, 初露锋芒
练习:
1.某学生在练习投篮时,篮球被抛出后,距离地面的高度h(米)和
飞行时间t(秒)满足下面的函数关系式:h=﹣t2+2t+2,则篮球距
离地面的最大高度是( )
A.8米 B.6米 C.4米 D.2米
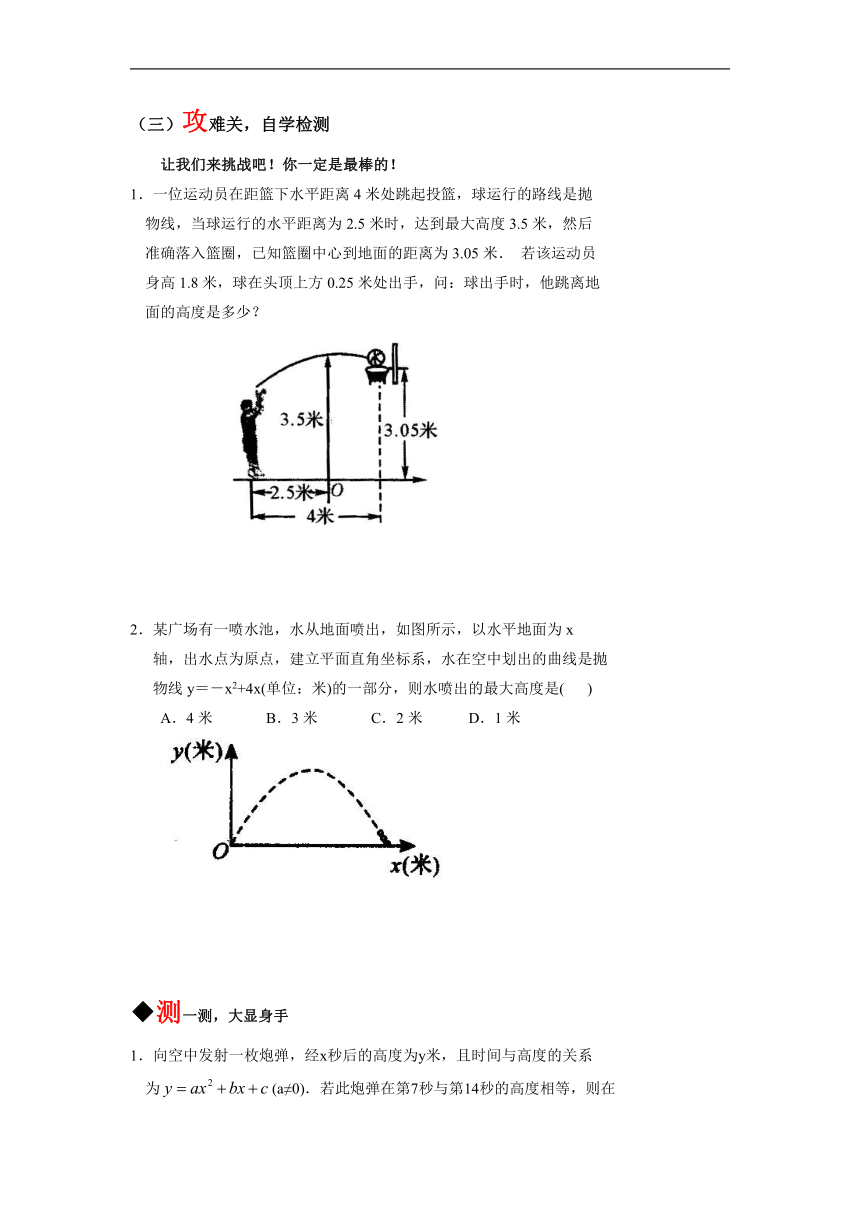
2.一位篮球运动员站在罚球线后投篮,球入篮得分.下列图象中,可以
大致反映篮球出手后到入篮框这一时间段内,篮球的高度h(米)
与时间t(秒)之间变化关系的是( )
A. B.
C. D.
(三)攻难关,自学检测
让我们来挑战吧!你一定是最棒的!
1.一位运动员在距篮下水平距离4米处跳起投篮,球运行的路线是抛
物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后
准确落入篮圈,已知篮圈中心到地面的距离为3.05米. 若该运动员
身高1.8米,球在头顶上方0.25米处出手,问:球出手时,他跳离地
面的高度是多少?
2.某广场有一喷水池,水从地面喷出,如图所示,以水平地面为x
轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛
物线y=-x2+4x(单位:米)的一部分,则水喷出的最大高度是( )
A.4米 B.3米 C.2米 D.1米
◆测一测,大显身手
1.向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系
为(a≠0).若此炮弹在第7秒与第14秒的高度相等,则在
下列时间中炮弹所在高度最高的是( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒
2.某烟花厂为庆祝大运会的圆满闭幕而专门研制了一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)之间的关系式是,若这种礼炮点火升空到最高处引爆,则从点火升空到引爆需要的时间为( )
A.3 s B.4 s C.5 s D.6 s
3.如图,铅球运动员掷铅球的高度(m)与水平距离(m)之间的函数关系式是:
,则该运动员此次掷铅球的成绩是 m.
4.一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下列函数关系式:h=-5(t-1)2+6,则小球距离地面的最大高度是( )
A.1米 B.5米 C.6米 D.7米
5.如图,一小孩将一只皮球从A处抛出去,它所经过的路线是某个二次函数图象的一部分,如果他的出手处A距地面的距离OA为1 m,球路的最高点B(8,9),求这个二次函数的表达式和小孩将球抛出了约多少米(精确到0.1 m) ?
参考答案
试身手, 初露锋芒
练习:
1.【答案】C
2.【答案】D
攻难关,自学检测
1.解:在直角坐标系中,点A(1.5,3.05)表示篮筐,点B(0,3.5)表示球运行的最大高度,点C表示球员篮球出手处,其横坐标为-2.5,
设C点的纵坐标为n,过点C、B、A所在的抛物线的解析式为y=ax2+c,由于抛物线开口向下,则点B(0,3.5)为顶点坐标,
∴ .
∵ 抛物线经过点A(1.5,3.05),
∴ 3.05=a·1.52+3.5,
∴ a=-0.2.
∴ 抛物线解析式为.
∴ ,
∴ n=2.25.
∴ 球出手时,球员跳离地面的高度为2.25-(1.8+0.25)=0.20(米).
答:球出手时,他跳离地面的高度是0.20米.
2.【答案】A
【解析】,当时,.
测一测,大显身手
1.【答案】B
【解析】根据抛物线的对称性知,抛物线的对称轴为x=10.5.即在第10秒中炮弹所在高度最高.
2.【答案】B
【解析】用配方法可把变形为,所以当t=4时,礼炮升到最高处引爆.
3.【答案】10
【解析】令,则: ,(舍去),.
4.【答案】C
【解析】t=1时,;
5.解:设,将点A代入,得
令,得
,,∴OC=8+≈16.5 (米)
答:解析式为:;小孩将球抛出了约16.5米.
-----利用二次函数解决投篮问题
知识链接
Hi,在开始挑战之前,先来热下身吧!
在实际问题中遇到最大(小)值问题时,往往先建立函数关系式,
如果是二次函数关系的,一般通过配方化为顶点式求解,也可以
用公式求解.
学习任务
(一)读教材,首战告捷
让我们一起来阅读教材,并做好色笔区分吧。
试身手, 初露锋芒
练习:
1.某学生在练习投篮时,篮球被抛出后,距离地面的高度h(米)和
飞行时间t(秒)满足下面的函数关系式:h=﹣t2+2t+2,则篮球距
离地面的最大高度是( )
A.8米 B.6米 C.4米 D.2米
2.一位篮球运动员站在罚球线后投篮,球入篮得分.下列图象中,可以
大致反映篮球出手后到入篮框这一时间段内,篮球的高度h(米)
与时间t(秒)之间变化关系的是( )
A. B.
C. D.
(三)攻难关,自学检测
让我们来挑战吧!你一定是最棒的!
1.一位运动员在距篮下水平距离4米处跳起投篮,球运行的路线是抛
物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后
准确落入篮圈,已知篮圈中心到地面的距离为3.05米. 若该运动员
身高1.8米,球在头顶上方0.25米处出手,问:球出手时,他跳离地
面的高度是多少?
2.某广场有一喷水池,水从地面喷出,如图所示,以水平地面为x
轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛
物线y=-x2+4x(单位:米)的一部分,则水喷出的最大高度是( )
A.4米 B.3米 C.2米 D.1米
◆测一测,大显身手
1.向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系
为(a≠0).若此炮弹在第7秒与第14秒的高度相等,则在
下列时间中炮弹所在高度最高的是( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒
2.某烟花厂为庆祝大运会的圆满闭幕而专门研制了一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)之间的关系式是,若这种礼炮点火升空到最高处引爆,则从点火升空到引爆需要的时间为( )
A.3 s B.4 s C.5 s D.6 s
3.如图,铅球运动员掷铅球的高度(m)与水平距离(m)之间的函数关系式是:
,则该运动员此次掷铅球的成绩是 m.
4.一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下列函数关系式:h=-5(t-1)2+6,则小球距离地面的最大高度是( )
A.1米 B.5米 C.6米 D.7米
5.如图,一小孩将一只皮球从A处抛出去,它所经过的路线是某个二次函数图象的一部分,如果他的出手处A距地面的距离OA为1 m,球路的最高点B(8,9),求这个二次函数的表达式和小孩将球抛出了约多少米(精确到0.1 m) ?
参考答案
试身手, 初露锋芒
练习:
1.【答案】C
2.【答案】D
攻难关,自学检测
1.解:在直角坐标系中,点A(1.5,3.05)表示篮筐,点B(0,3.5)表示球运行的最大高度,点C表示球员篮球出手处,其横坐标为-2.5,
设C点的纵坐标为n,过点C、B、A所在的抛物线的解析式为y=ax2+c,由于抛物线开口向下,则点B(0,3.5)为顶点坐标,
∴ .
∵ 抛物线经过点A(1.5,3.05),
∴ 3.05=a·1.52+3.5,
∴ a=-0.2.
∴ 抛物线解析式为.
∴ ,
∴ n=2.25.
∴ 球出手时,球员跳离地面的高度为2.25-(1.8+0.25)=0.20(米).
答:球出手时,他跳离地面的高度是0.20米.
2.【答案】A
【解析】,当时,.
测一测,大显身手
1.【答案】B
【解析】根据抛物线的对称性知,抛物线的对称轴为x=10.5.即在第10秒中炮弹所在高度最高.
2.【答案】B
【解析】用配方法可把变形为,所以当t=4时,礼炮升到最高处引爆.
3.【答案】10
【解析】令,则: ,(舍去),.
4.【答案】C
【解析】t=1时,;
5.解:设,将点A代入,得
令,得
,,∴OC=8+≈16.5 (米)
答:解析式为:;小孩将球抛出了约16.5米.
同课章节目录
