22.1.4 二次函数y=ax^2+bx+c的图象与性质 学案(含答案)
文档属性
| 名称 | 22.1.4 二次函数y=ax^2+bx+c的图象与性质 学案(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 292.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-15 18:00:43 | ||
图片预览




文档简介
二次函数y=ax2+bx+c(a≠0)的图象与性质
知识链接
Hi,在开始挑战之前,先来热下身吧!
1.一般地,形如 (a,b,c是常数,a≠0)的函数叫做二次函数,其中
__ _是自变量,a,b,c分别是函数解析式的____项系数和___ _
项系数、___ 项.
2.将二次函数y=-(x-1)2-3(x-1)化成y=ax2+bx+c的形式为 .
学习任务
(一)读教材,首战告捷
让我们一起来阅读教材,并做好色笔区分吧。
(二) 试身手, 初露锋芒
让我们来试试下面的问题和小练习吧。
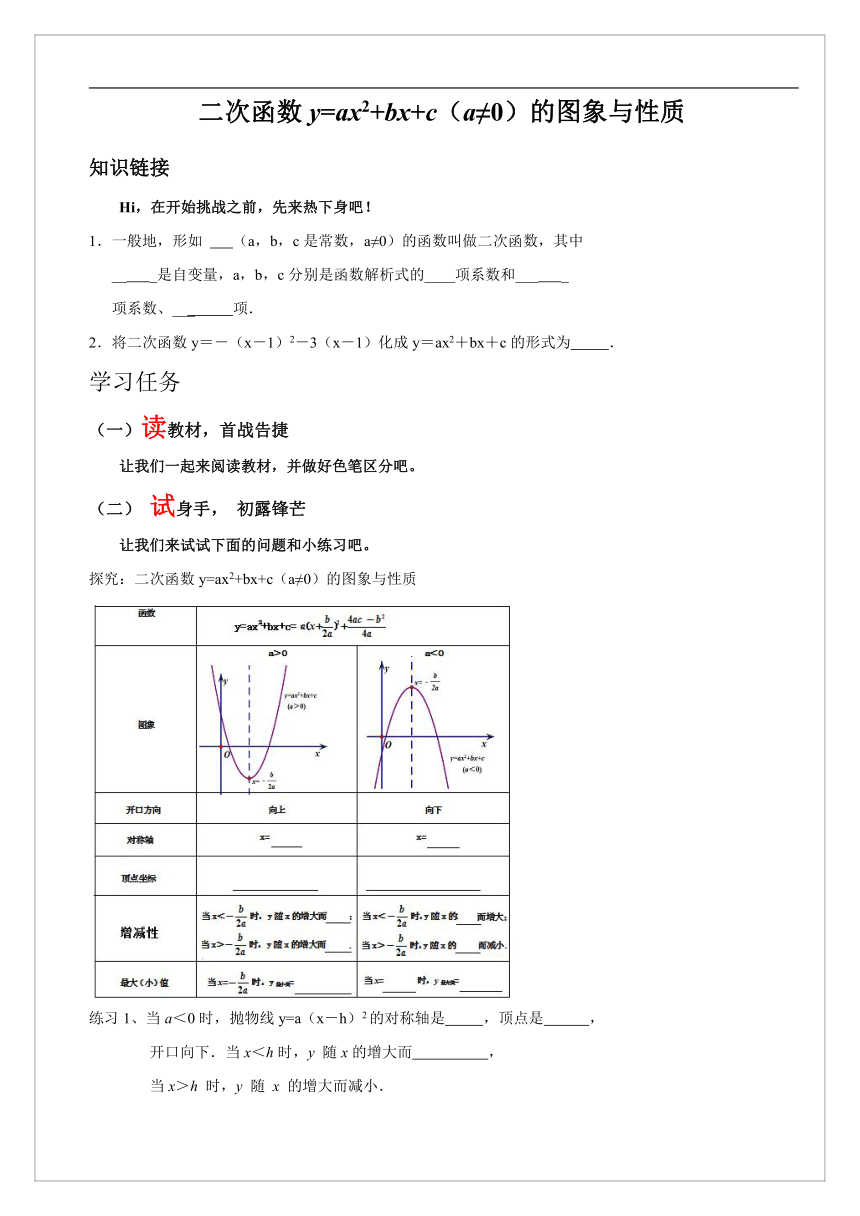
探究:二次函数y=ax2+bx+c(a≠0)的图象与性质
练习1、当a<0时,抛物线y=a(x-h)2的对称轴是 ,顶点是 ,
开口向下.当x<h时,y 随x的增大而 ,
当x>h 时,y 随 x 的增大而减小.
练习2、抛物线y=a(x-h)2 +k有如下特点:
(1)当 a>0 时,开口 ;当 a<0 时,开口向下.
(2)对称轴为直线 .
(3)顶点坐标(h,k).
如果 a>0,当 x<h 时,y 随 x 的增大而 ,
当 x>h 时,y 随 x 的增大而增大;
如果 a<0,当 x<h 时,y 随 x 的增大而增大,
当 x>h 时,y 随 x 的增大而减小.
(三)攻难关,自学检测
让我们来挑战吧!你一定是最棒的!
1.已知抛物线y=ax2+bx+c的对称轴为x=2,且经过点(3,0),则a+b+c
的值( )
A.等于0 B.等于1 C. 等于-1 D.不能确定
2.二次函数y=ax2+bx+c(a≠0)
(1)对称轴: ;(2) 顶点坐标: .
3.如图所示,抛物线的对称轴是x=1,与x轴交于A、B两点,点B的
坐标为(,0),则点A的坐标是_______.
4.将二次函数一般式y=ax2+bx+c化成顶点式.
5.请写出抛物线y= 的开口方向、对称轴、顶点坐标、
最值和变化趋势.
6.已知抛物线:
(1)求抛物线的开口方向、对称轴和顶点坐标;
(2)画函数图象,并根据图象说出x取何值时,y随x的增大而增大?
x取何值时,y随x的增大而减小?函数y有最大值还是最小值?
最值为多少?
◆测一测,大显身手
1.已知二次函数中,其函数y与自变量x之间的部分对应值如下表所示:
x …… 0 1 2 3 4 ……
y …… 4 1 0 1 4 ……
点A(x1,y1),B(x2,y2)在函数的图象上,则当1<x1<2,3<x2<4时,y1与y2的大小关系正确的
是( )
A.y1>y2 B.y1<y2 C.y1≥y2 D.y1≤y2
2.已知二次函数的图象(0≤x≤3)如图所示,关于该函数在自变量取值范围内,下列说法正确的是( )
A.有最小值0,有最大值3 B.有最小值-1,有最大值0
C.有最小值-1,有最大值3 D.有最小值-1,无最大值
3.已知抛物线y=x2+x+b2经过点,则y1的值是___ __.
4.求抛物线的对称轴和顶点坐标.
5.通过配方确定 y=-2x2+4x+6 的开口方向、对称轴和顶点坐标,并指出其增减性.
参考答案
试身手, 初露锋芒
练习1、【答案】x = h;(h,0);增大.
练习2、【答案】向上;x = h;减小.
攻难关,自学检测
1.【答案】A
【解析】因为抛物线y=ax2+bx+c的对称轴为x=2,且经过点(3,0),所以过点(1,0)代入解析式
得a+b+c=0.
2.【答案】(1)x=;(2)
3.【答案】,
【解析】由抛物线的对称性知,A、B两点关于直线x=1对称,设点A的坐标是(x1,0)则有,所以,即点A的坐标是,.
4.解:y=ax2+bx+c=a( )
=a[]
=a( )2+
5.解:y=
∵a= , b=-2 ,c=-1
(1)(因为a=>0)开口:向上
(2)对称轴:x==
(3)顶点坐标:
∵=
∴顶点坐标:(2,-3);
(4)(因为a=>0,抛物线开口向上,所以图象有最低点,即函数有最小值)
当x=2时,y最小值=-3
(5)当x<2时,y随x的增大而减小;当x>2时,y随x的增大而增大.
6.【解析】
解:(1)∵ ,b=-3,∴,
把x=-3代入解析式得,.
∴抛物线的开口向下,对称轴是直线x=-3,顶点坐标是(-3,2).
(2)由于抛物线的顶点坐标为A(-3,2),对称轴为x=-3.
抛物线与x轴两交点为B(-5,0)和C(-1,0),与y轴的交点为,
取D关于对称轴的对称点,
用平滑曲线顺次连结,便得到二次函数的图象,如图所示.
从图象可以看出:
在对称轴左侧,即当x<-3时,y随x的增大而增大;
在对称轴右侧,即当x>-3时,y随x的增大而减小.
因为抛物线的开口向下,顶点A是抛物线的最高点,
所以函数有最大值,当x=-3时,.
测一测,大显身手
1.【答案】B
【解析】由表可知1<x1<2,∴ 0<y1<1;3<x2<4,∴ 1<y2<4,故y1<y2.
2.【答案】C
【解析】观察图象在0≤x≤3时的最低点为(1,-1),最高点为(3,3),故有最小值-1,有最大值3.
3.【答案】
【解析】
又因为函数图象经过,所以,代入即可求得.
4.【答案与解析】
解法1(配方法):
.
∴顶点坐标为,对称轴为直线.
解法2(公式法):∵ ,,,
∴ ,.
∴ 顶点坐标为,对称轴为直线.
解法3(代入法):∵ ,,,
∴ .
将代入解析式中得,.
∴ 顶点坐标为,对称轴为直线.
5.【答案与解析】
解:y=-2x2+4x+6=-2(x-1)2+8.
∴抛物线开口向下,对称轴是直线 x=1,顶点坐标为(1,8).
当x<1 时,y 随 x 的增大而增大;当x>1 时,y 随 x 的增大而减小.
知识链接
Hi,在开始挑战之前,先来热下身吧!
1.一般地,形如 (a,b,c是常数,a≠0)的函数叫做二次函数,其中
__ _是自变量,a,b,c分别是函数解析式的____项系数和___ _
项系数、___ 项.
2.将二次函数y=-(x-1)2-3(x-1)化成y=ax2+bx+c的形式为 .
学习任务
(一)读教材,首战告捷
让我们一起来阅读教材,并做好色笔区分吧。
(二) 试身手, 初露锋芒
让我们来试试下面的问题和小练习吧。
探究:二次函数y=ax2+bx+c(a≠0)的图象与性质
练习1、当a<0时,抛物线y=a(x-h)2的对称轴是 ,顶点是 ,
开口向下.当x<h时,y 随x的增大而 ,
当x>h 时,y 随 x 的增大而减小.
练习2、抛物线y=a(x-h)2 +k有如下特点:
(1)当 a>0 时,开口 ;当 a<0 时,开口向下.
(2)对称轴为直线 .
(3)顶点坐标(h,k).
如果 a>0,当 x<h 时,y 随 x 的增大而 ,
当 x>h 时,y 随 x 的增大而增大;
如果 a<0,当 x<h 时,y 随 x 的增大而增大,
当 x>h 时,y 随 x 的增大而减小.
(三)攻难关,自学检测
让我们来挑战吧!你一定是最棒的!
1.已知抛物线y=ax2+bx+c的对称轴为x=2,且经过点(3,0),则a+b+c
的值( )
A.等于0 B.等于1 C. 等于-1 D.不能确定
2.二次函数y=ax2+bx+c(a≠0)
(1)对称轴: ;(2) 顶点坐标: .
3.如图所示,抛物线的对称轴是x=1,与x轴交于A、B两点,点B的
坐标为(,0),则点A的坐标是_______.
4.将二次函数一般式y=ax2+bx+c化成顶点式.
5.请写出抛物线y= 的开口方向、对称轴、顶点坐标、
最值和变化趋势.
6.已知抛物线:
(1)求抛物线的开口方向、对称轴和顶点坐标;
(2)画函数图象,并根据图象说出x取何值时,y随x的增大而增大?
x取何值时,y随x的增大而减小?函数y有最大值还是最小值?
最值为多少?
◆测一测,大显身手
1.已知二次函数中,其函数y与自变量x之间的部分对应值如下表所示:
x …… 0 1 2 3 4 ……
y …… 4 1 0 1 4 ……
点A(x1,y1),B(x2,y2)在函数的图象上,则当1<x1<2,3<x2<4时,y1与y2的大小关系正确的
是( )
A.y1>y2 B.y1<y2 C.y1≥y2 D.y1≤y2
2.已知二次函数的图象(0≤x≤3)如图所示,关于该函数在自变量取值范围内,下列说法正确的是( )
A.有最小值0,有最大值3 B.有最小值-1,有最大值0
C.有最小值-1,有最大值3 D.有最小值-1,无最大值
3.已知抛物线y=x2+x+b2经过点,则y1的值是___ __.
4.求抛物线的对称轴和顶点坐标.
5.通过配方确定 y=-2x2+4x+6 的开口方向、对称轴和顶点坐标,并指出其增减性.
参考答案
试身手, 初露锋芒
练习1、【答案】x = h;(h,0);增大.
练习2、【答案】向上;x = h;减小.
攻难关,自学检测
1.【答案】A
【解析】因为抛物线y=ax2+bx+c的对称轴为x=2,且经过点(3,0),所以过点(1,0)代入解析式
得a+b+c=0.
2.【答案】(1)x=;(2)
3.【答案】,
【解析】由抛物线的对称性知,A、B两点关于直线x=1对称,设点A的坐标是(x1,0)则有,所以,即点A的坐标是,.
4.解:y=ax2+bx+c=a( )
=a[]
=a( )2+
5.解:y=
∵a= , b=-2 ,c=-1
(1)(因为a=>0)开口:向上
(2)对称轴:x==
(3)顶点坐标:
∵=
∴顶点坐标:(2,-3);
(4)(因为a=>0,抛物线开口向上,所以图象有最低点,即函数有最小值)
当x=2时,y最小值=-3
(5)当x<2时,y随x的增大而减小;当x>2时,y随x的增大而增大.
6.【解析】
解:(1)∵ ,b=-3,∴,
把x=-3代入解析式得,.
∴抛物线的开口向下,对称轴是直线x=-3,顶点坐标是(-3,2).
(2)由于抛物线的顶点坐标为A(-3,2),对称轴为x=-3.
抛物线与x轴两交点为B(-5,0)和C(-1,0),与y轴的交点为,
取D关于对称轴的对称点,
用平滑曲线顺次连结,便得到二次函数的图象,如图所示.
从图象可以看出:
在对称轴左侧,即当x<-3时,y随x的增大而增大;
在对称轴右侧,即当x>-3时,y随x的增大而减小.
因为抛物线的开口向下,顶点A是抛物线的最高点,
所以函数有最大值,当x=-3时,.
测一测,大显身手
1.【答案】B
【解析】由表可知1<x1<2,∴ 0<y1<1;3<x2<4,∴ 1<y2<4,故y1<y2.
2.【答案】C
【解析】观察图象在0≤x≤3时的最低点为(1,-1),最高点为(3,3),故有最小值-1,有最大值3.
3.【答案】
【解析】
又因为函数图象经过,所以,代入即可求得.
4.【答案与解析】
解法1(配方法):
.
∴顶点坐标为,对称轴为直线.
解法2(公式法):∵ ,,,
∴ ,.
∴ 顶点坐标为,对称轴为直线.
解法3(代入法):∵ ,,,
∴ .
将代入解析式中得,.
∴ 顶点坐标为,对称轴为直线.
5.【答案与解析】
解:y=-2x2+4x+6=-2(x-1)2+8.
∴抛物线开口向下,对称轴是直线 x=1,顶点坐标为(1,8).
当x<1 时,y 随 x 的增大而增大;当x>1 时,y 随 x 的增大而减小.
同课章节目录
