23.2 中心对称 学案(含答案)
图片预览

文档简介
23.2中心对称
知识链接
Hi,在开始挑战之前,先来热下身吧!
理解中心对称和中心对称图形的定义和性质,掌握他们之间的区别
和联系.
学习任务
(一)读教材,首战告捷
让我们一起来阅读教材,并做好色笔区分吧。
试身手, 初露锋芒
一、中心对称
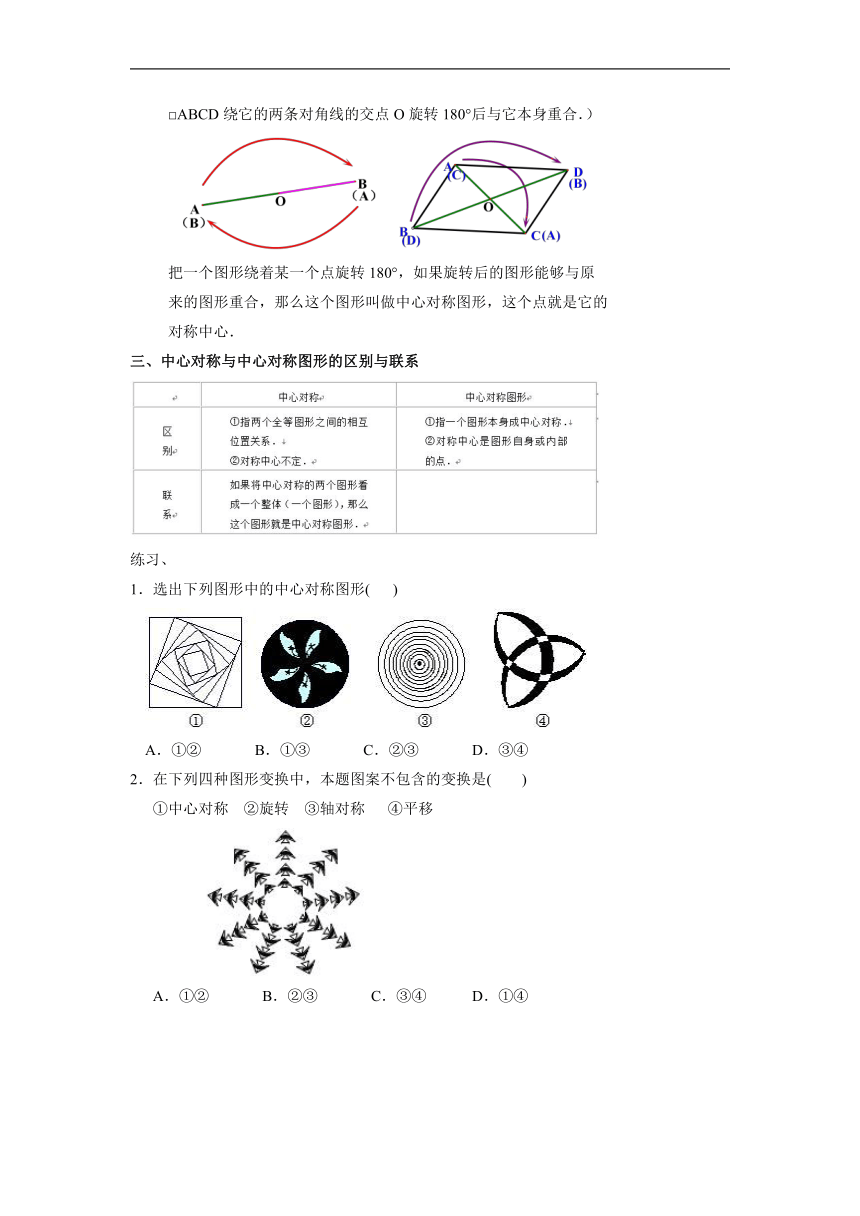
(如图所示,△OAB绕着O点旋转180°后与△OCD重合.)
把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,
那么就说这两个图形关于这个点对称或中心对称,这个点叫做________.
这两个图形中的对应点叫做关于中心的对称点.
(如A与C点,B与D点)(由定义可得中心对称的性质)
1.中心对称的两个图形,对称点所连线段都经过对称中心,而且被对
称中心所_______;
(如O,A,C三点共线,且O是AC的中点,OA=OC;)
2.中心对称的两个图形是全等图形.
(△OAB≌△OCD,对应边和对应角相等)
二、中心对称图形
(如图所示,线段AB绕它的中点旋转180°后与它本身重合,
□ABCD绕它的两条对角线的交点O旋转180°后与它本身重合.)
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原
来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的
对称中心.
三、中心对称与中心对称图形的区别与联系
练习、
1.选出下列图形中的中心对称图形( )
A.①② B.①③ C.②③ D.③④
2.在下列四种图形变换中,本题图案不包含的变换是( )
①中心对称 ②旋转 ③轴对称 ④平移
A.①② B.②③ C.③④ D.①④
(三)攻难关,自学检测
让我们来挑战吧!你一定是最棒的!
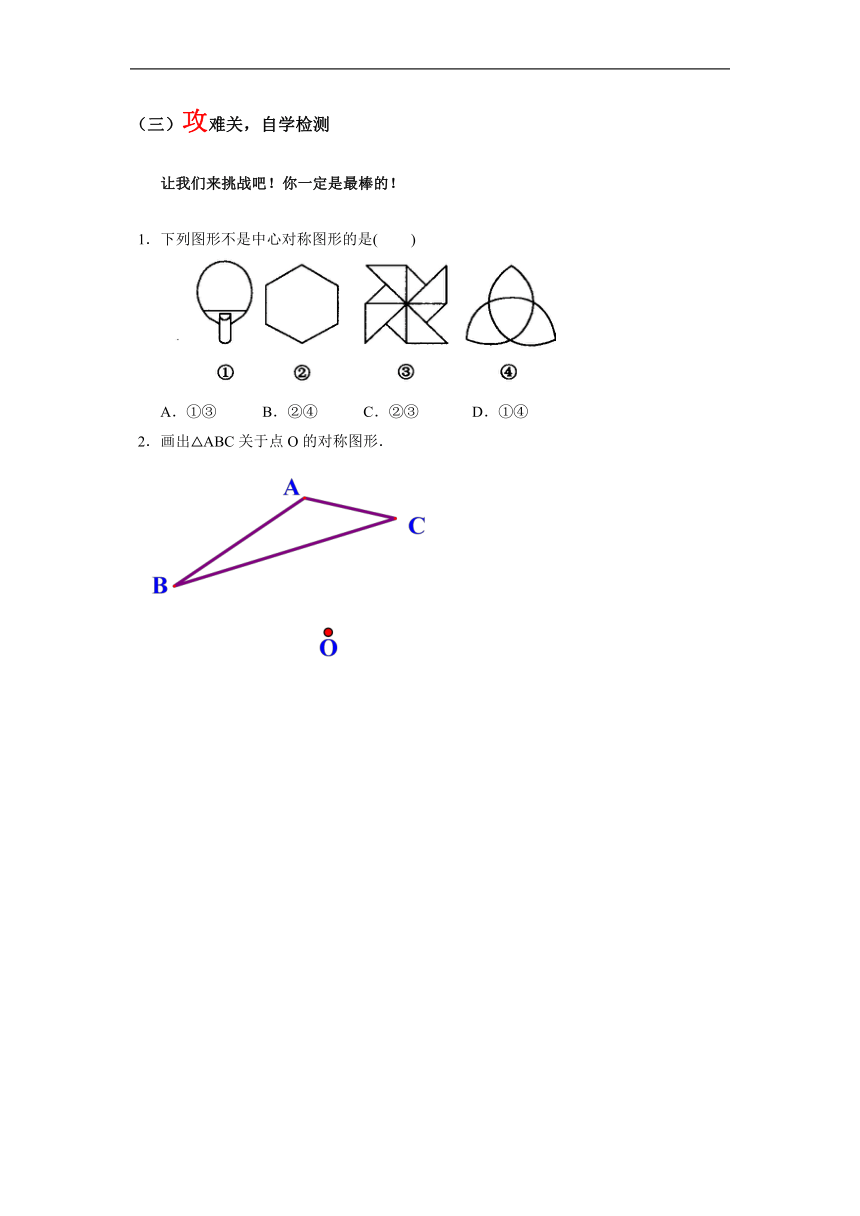
1.下列图形不是中心对称图形的是( )
A.①③ B.②④ C.②③ D.①④
2.画出△ABC关于点O的对称图形.
◆测一测,大显身手
一、选择题
1.如图,若正方形EFGH由正方形ABCD绕某点旋转得到,则可以作为旋转中
心的是( )
A.M或O或N B.E或O或C
C.E或O或N D.M或O或C
2.下列说法中,不正确的是( )
A.轴对称图形的对称轴是对称点连线的垂直平分线
B.中心对称图形的对称中心是对称点连线的中点
C.成轴对称的两个图形中,对应线段相等
D.成中心对称的两个图形中,对应线段平行且相等
3.在线段、等腰梯形、平行四边形、矩形、菱形、正方形、等边三角形中,既是轴对称图形,又是中心对称图形的图形有( )
A.3个 B.4个 C.5个 D.6个
4.下列说法正确的是( )
A.两个会重合的三角形一定成轴对称
B.两个会重合的三角形一定成中心对称
C.成轴对称的两个图形中,对称线段平行且相等
D.成中心对称的两个图形中,对称线段平行(或在同一条直线上)且相等
二、解答题
5.如图,△DEF是由△ABC绕点O顺时针旋转180°后得到的图形.
(1)请指出图中所有相等的线段;
(2)写出图中所有相等的角;
(3)图中哪些三角形可以看成是关于点O成中心对称的?
参考答案
试身手, 初露锋芒
一、对称中心(简称中心);平分
三、如果把中心对称图形对称的部分看成是两个图形,那么它们又关于中心对称.
练习、
1.【答案】B
2.【答案】D
【解析】旋转180°与原图像不能重合,所以①是错误的;
平移应该是整个图形通过平移得到新图形,所以④是错误的.
攻难关,自学检测
1.【答案】D
(提示:中心对称图形要求绕中心旋转180°与原图形重合,①④两个图形绕中心旋转180°不能与原图形重合,所以选D.)
2.连接AO,并延长至A′点,使得OA′=OA,则A′就是A点关于点O的对称点,同理画出B,C点的对称点B′,C′,顺次连接这三个对称点得△A′B′C′,则此三角形就是所求画的△ABC关于点O的对称图形.
测一测,大显身手
1.【答案】A
2.【答案】D
3.【答案】B
【解析】既是轴对称图形,又是中心对称图形的图形有线段、矩形、菱形、正方形.
4.【答案】D
5.【解析】因为△DEF是由△ABC绕点O顺时针旋转180°后得到的,
所以这两个三角形关于点O成中心对称
(1)图中相等的线段有:
(2)图中相等的角有:
(3)图中关于点O成中心对称的三角形有:
△ABC与△DEF,△ABO与△DEO,△ACO与△DFO,△BCO与△EFO.
知识链接
Hi,在开始挑战之前,先来热下身吧!
理解中心对称和中心对称图形的定义和性质,掌握他们之间的区别
和联系.
学习任务
(一)读教材,首战告捷
让我们一起来阅读教材,并做好色笔区分吧。
试身手, 初露锋芒
一、中心对称
(如图所示,△OAB绕着O点旋转180°后与△OCD重合.)
把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,
那么就说这两个图形关于这个点对称或中心对称,这个点叫做________.
这两个图形中的对应点叫做关于中心的对称点.
(如A与C点,B与D点)(由定义可得中心对称的性质)
1.中心对称的两个图形,对称点所连线段都经过对称中心,而且被对
称中心所_______;
(如O,A,C三点共线,且O是AC的中点,OA=OC;)
2.中心对称的两个图形是全等图形.
(△OAB≌△OCD,对应边和对应角相等)
二、中心对称图形
(如图所示,线段AB绕它的中点旋转180°后与它本身重合,
□ABCD绕它的两条对角线的交点O旋转180°后与它本身重合.)
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原
来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的
对称中心.
三、中心对称与中心对称图形的区别与联系
练习、
1.选出下列图形中的中心对称图形( )
A.①② B.①③ C.②③ D.③④
2.在下列四种图形变换中,本题图案不包含的变换是( )
①中心对称 ②旋转 ③轴对称 ④平移
A.①② B.②③ C.③④ D.①④
(三)攻难关,自学检测
让我们来挑战吧!你一定是最棒的!
1.下列图形不是中心对称图形的是( )
A.①③ B.②④ C.②③ D.①④
2.画出△ABC关于点O的对称图形.
◆测一测,大显身手
一、选择题
1.如图,若正方形EFGH由正方形ABCD绕某点旋转得到,则可以作为旋转中
心的是( )
A.M或O或N B.E或O或C
C.E或O或N D.M或O或C
2.下列说法中,不正确的是( )
A.轴对称图形的对称轴是对称点连线的垂直平分线
B.中心对称图形的对称中心是对称点连线的中点
C.成轴对称的两个图形中,对应线段相等
D.成中心对称的两个图形中,对应线段平行且相等
3.在线段、等腰梯形、平行四边形、矩形、菱形、正方形、等边三角形中,既是轴对称图形,又是中心对称图形的图形有( )
A.3个 B.4个 C.5个 D.6个
4.下列说法正确的是( )
A.两个会重合的三角形一定成轴对称
B.两个会重合的三角形一定成中心对称
C.成轴对称的两个图形中,对称线段平行且相等
D.成中心对称的两个图形中,对称线段平行(或在同一条直线上)且相等
二、解答题
5.如图,△DEF是由△ABC绕点O顺时针旋转180°后得到的图形.
(1)请指出图中所有相等的线段;
(2)写出图中所有相等的角;
(3)图中哪些三角形可以看成是关于点O成中心对称的?
参考答案
试身手, 初露锋芒
一、对称中心(简称中心);平分
三、如果把中心对称图形对称的部分看成是两个图形,那么它们又关于中心对称.
练习、
1.【答案】B
2.【答案】D
【解析】旋转180°与原图像不能重合,所以①是错误的;
平移应该是整个图形通过平移得到新图形,所以④是错误的.
攻难关,自学检测
1.【答案】D
(提示:中心对称图形要求绕中心旋转180°与原图形重合,①④两个图形绕中心旋转180°不能与原图形重合,所以选D.)
2.连接AO,并延长至A′点,使得OA′=OA,则A′就是A点关于点O的对称点,同理画出B,C点的对称点B′,C′,顺次连接这三个对称点得△A′B′C′,则此三角形就是所求画的△ABC关于点O的对称图形.
测一测,大显身手
1.【答案】A
2.【答案】D
3.【答案】B
【解析】既是轴对称图形,又是中心对称图形的图形有线段、矩形、菱形、正方形.
4.【答案】D
5.【解析】因为△DEF是由△ABC绕点O顺时针旋转180°后得到的,
所以这两个三角形关于点O成中心对称
(1)图中相等的线段有:
(2)图中相等的角有:
(3)图中关于点O成中心对称的三角形有:
△ABC与△DEF,△ABO与△DEO,△ACO与△DFO,△BCO与△EFO.
同课章节目录
