21.3.3 实际问题与一元二次方程之数字、几何动态问题 学案(含答案)
文档属性
| 名称 | 21.3.3 实际问题与一元二次方程之数字、几何动态问题 学案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 98.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-15 18:00:43 | ||
图片预览



文档简介
人教版九年级数学第二十一章
21.3实际问题与一元二次方程之数字、几何动态问题
知识链接
Hi,在开始挑战之前,先来热下身吧!
1.几个连续偶数(或奇数)中,相邻两个偶数(或奇数)相差 .
2.三个连续整数,设中间一个数为x,则另两个数分别为x-1, .
学习任务
(一)读教材,首战告捷
让我们一起来阅读教材,并做好色笔区分吧。
(二) 试身手, 初露锋芒
让我们来试试下面的问题和小练习吧。
复习:
两位数:a×10+b;
三位数:a×100+b×10+c;
偶数:2n(n为整数);
奇数:2n+1(或2n-1)(n为整数).
练习1、若一个一元二次方程的两个根分别是Rt△ABC的两条直角边长,
且S△ABC=3,请写出一个符合题意的一元二次方程 .
练习2、元旦期间,一个小组有若干人,新年互送贺卡一张,已知全组共
送贺卡132张,则这个小组共有( )
A.11人 B.12人 C.13人 D.14人
(三)攻难关,自学检测
让我们来挑战吧!你一定是最棒的!
一、选择题
1.一个跳水运动员从距离水面10米高的跳台向上跳起0.5米,开始做翻
滚动作,它在空中每完成一个动作需要时间0.2秒,并至少在离水面3.5
米处停止翻滚动作准备入水,最后入水速度为14米/秒,该运动员在空中
至多做翻滚动作( )
A.3个 B.4个 C.5个 D.6个
2.甲、乙两人分别骑车从A、B两地相向而行,甲先行1小时后,乙才出
发,又经过4小时两人在途中的C地相遇,相遇后两人按原来的方向继续
前进.乙在由C地到达A地的途中因故停了20分钟,结果乙由C地到达A
地时比甲由C地到达B地还提前了40分钟,已知乙比甲每小时多行驶4
千米,则甲、乙两人骑车的速度分别为( )千米/时.
A.2,6 B.12,16 C.16,20 D.20,24
二、填空题
3.若两数的和是2,两数的平方和是74,则这两数为________.
4.有一个两位数,它的十位数字与个位数字之和是8,如果把十位数字与
个位数字调换后,所得的两位数乘原来的两位数就得1855,则原来的两
位数是 .
三、解答题
5.(1)有一个两位数等于其数字之积的3倍,其十位数字比个位数字小2,
求这两位数.
(2)两个连续奇数的积是323,求这两个连续奇数.
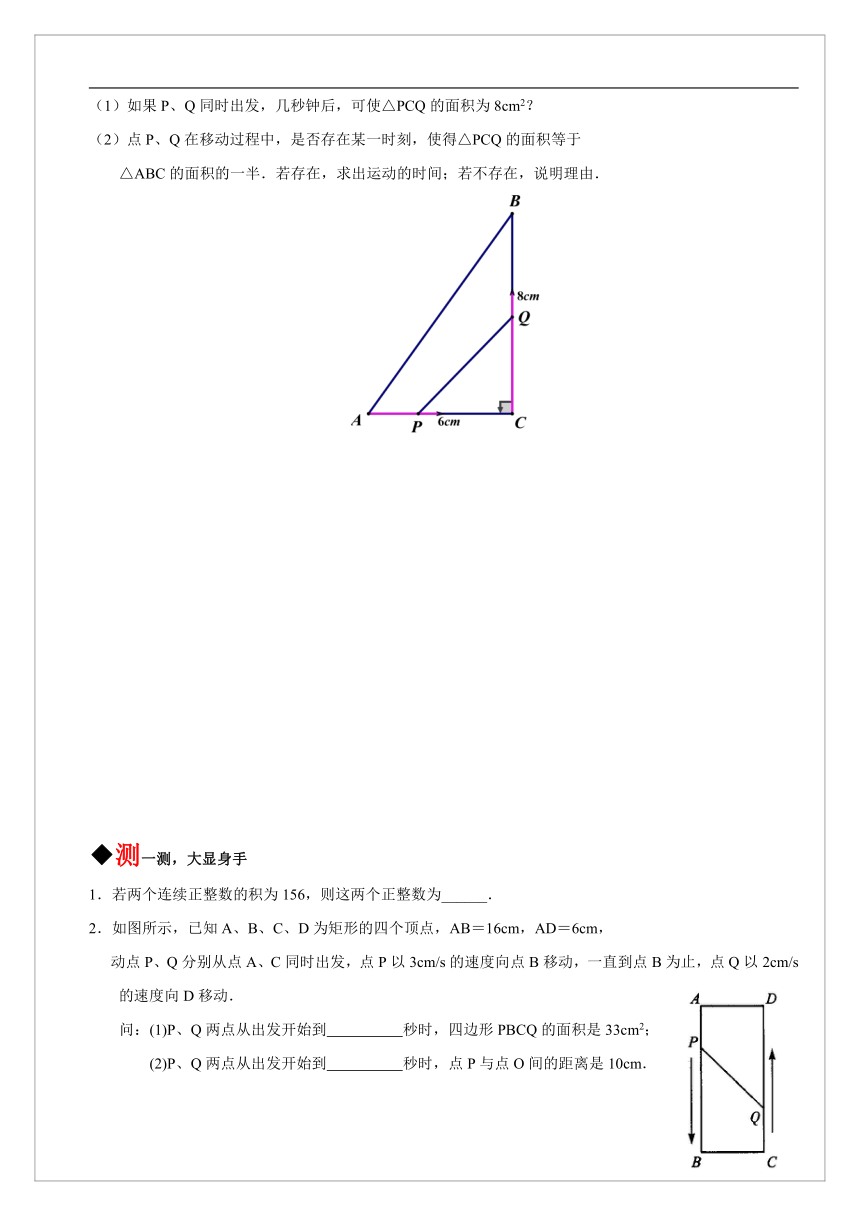
6.如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P
从A向C运动,点Q同时从C向B运动,速度分别为1cm/s,2cm/s.
当其中一点到达终点时两点同时停止运动.
(1)如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8cm2?
(2)点P、Q在移动过程中,是否存在某一时刻,使得△PCQ的面积等于
△ABC的面积的一半.若存在,求出运动的时间;若不存在,说明理由.
◆测一测,大显身手
1.若两个连续正整数的积为156,则这两个正整数为______.
2.如图所示,已知A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,
动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到点B为止,点Q以2cm/s的速度向D移动.
问:(1)P、Q两点从出发开始到 秒时,四边形PBCQ的面积是33cm2;
(2)P、Q两点从出发开始到 秒时,点P与点O间的距离是10cm.
3.有一个两位数,个位数字与十位数字的和为14,交换数字位置后,得到新的两位数,比这两个数字的积还大38,求这个两位数.
4.已知两个数的和等于12,积等于32,求这两个数是多少.
5.如图所示,AO=OB=50cm,OC是一条射线,OC⊥AB,一只蚂蚁由A点以2cm/s的速度向B爬行,同时另一只蚂蚁由O点以3 cm/s的速度沿OC方向爬行,是否存在这样的时刻,使两只蚂蚁与O点组成的三角形的面积为450cm2
参考答案
试身手, 初露锋芒
练习1、【答案】 x2-5x+6=0.
【提示】本题是结论开放的题(答案不唯一).
练习2、【答案】B
【提示】设这个小组共x人,则x(x-1)=132,x1=-11(舍去),x2=12.
攻难关,自学检测
1.【答案】D
【解析】从10.5米高处到入水过程的平均速度为7米/秒,所用时间为10.5÷7=1.5秒,
速度每秒变化米/秒.设运动员从最高处到离水面3.5米时用时x秒,
那么这段距离的平均速度为x2=1.5,x≈1.2,1.2÷0.2=6,最多做6个翻滚动作.
2.【答案】C
【解析】设甲的速度为x千米/时,则乙的速度为(x+4)千米/时.
根据题意,得
解之,得x1=16,x2=-2.
经检验:x1=16,x2=-2都是原方程的根,但x2=-2不合题意,舍去.
∴当x=16时,x+4=20.
3.【答案】-5和7
【解析】设两数中一个数为x,则另一个数为2-x.
根据题意得x2+(2-x)2=74,解得x1=-5,x2=7.
当x=-5时,另一个数为7;
当x=7时,另一个数为-5,
所以这两个数为-5和7.
4.【答案】35或53
【解析】设原两位数的十位数字为x,则个位数字是(8-x),由题意得
[10x+(8-x)]·[10(8-x)+x]=1855.
化简得x2-8x+15=0,
解之得:x1=3,x2=5.
经检验,x1=3,x2=5都符合题意.
答:原两位数是35或53.
5.解:(1)设十位数字为a,则个位数字为a+2.
依题意,得:11a+2=3×a×(a+2)
整理,得:3a2-5a-2=0
解之得:a1=2,a2=(不合题意,舍去) .
答:这个两位数为24.
(2)设较小的奇数为:2n-1,则较大的奇数为:2n+1.
依题意,得:(2n-1)(2n+1)=323
整理,得:n2-81=0
解之得:n1= 9,n2=-9(不合题意,舍去).
则2n-1=18-1=17,2n+1=18+1=19.
答:这两个连续奇数为17和19.
6.解:(1)设t秒钟之后△PCQ的面积为8cm2.
依题意,得:S△PCQ=PC·QC= (6-t)× 2t=8
整理,得:t2-6t+8=0
解之得:t1=2, t2=4.
答:P、Q同时出发2秒或4秒后,可使△PCQ的面积为8cm2.
(2)假设存在这样的时刻,
依题意,得:S△PCQ=PC·QC= (6-t)× 2t=S△ABC=×24=12
整理,得:t2-6t+12=0
∵△=(-6)2-4×12=36-48=-12<0
∴方程无实数根.
即不存在这样的时间点使得△PCQ的面积等于△ABC的面积的一半.
测一测,大显身手
1.【答案】12和13
2.【答案】(1)5秒;(2)秒或秒.
【解析】(1)设P、Q两点从出发开始到x秒时,四边形PBCQ的面积是33cm2,
则AP=3x,PB=16-3x,CQ=2x,由梯形的面积公式得,
解得x=5.
答:P、Q两点从出发开始到5秒时,四边形PBCO的面积为33cm2.
(2)设P、Q两点从出发开始到y秒时,点P、点Q间的距离为10cm.
过点Q作QH⊥AB,交AB于H,如答图3所示,
则AP=3y,CQ=2y,PH=16-3y-2y,
根据勾股定理.得(16-3y-2y)2=102-62,化简方程得(16-5y)2=64,
解得,.
答:P、Q两点从出发开始到秒或秒时,点P、点Q间的距离是10cm.
3.【解析】解:设个位数字为x,则十位数字为14-x,两数字之积为x(14-x),
两个数字颠倒后的数为10x+(14-x).
根据题意,得10x+(14-x)-x(14-x)=38.
整理,得x2-5x-24=0,
∴ (x-8)(x+3)=0,∴x1=8,x2=-3.
∵个位上的数字不可能是负数,∴x=-3舍去.
当x=8时,14-x=6,∴原数为68.
答:这个两位数是68.
4.【答案】解:设其中一个数为x,那么另一个数可表示为(12-x),依题意得x(12-x)=32,
整理得x2-12x+32=0
解得 x1=4,x2=8,
当x=4时12-x=8;
当x=8时12-x=4.
所以这两个数是4和8.
5.【答案】解:(1)当蚂蚁在AO段时,设离开A点t s后两只蚂蚁与O点组成的三角形的面积是450cm2.
根据题意,得.
整理得:,
解得t1=10,t2=15.
(2)当蚂蚁爬完AO这段距离用了后,开始由O向B爬行,设从O点开始x s后组成的
三角形的面积是450 cm2,根据题意,得:,
整理得x2+25x-150=0,解得x1=5,x2=-30(舍去).
当x=5时,x+25=30.这时蚂蚁已由A点爬了30s.
答:分别在10s,15s,30s时,两只蚂蚁与O点组成的三角形的面积是450cm2.
21.3实际问题与一元二次方程之数字、几何动态问题
知识链接
Hi,在开始挑战之前,先来热下身吧!
1.几个连续偶数(或奇数)中,相邻两个偶数(或奇数)相差 .
2.三个连续整数,设中间一个数为x,则另两个数分别为x-1, .
学习任务
(一)读教材,首战告捷
让我们一起来阅读教材,并做好色笔区分吧。
(二) 试身手, 初露锋芒
让我们来试试下面的问题和小练习吧。
复习:
两位数:a×10+b;
三位数:a×100+b×10+c;
偶数:2n(n为整数);
奇数:2n+1(或2n-1)(n为整数).
练习1、若一个一元二次方程的两个根分别是Rt△ABC的两条直角边长,
且S△ABC=3,请写出一个符合题意的一元二次方程 .
练习2、元旦期间,一个小组有若干人,新年互送贺卡一张,已知全组共
送贺卡132张,则这个小组共有( )
A.11人 B.12人 C.13人 D.14人
(三)攻难关,自学检测
让我们来挑战吧!你一定是最棒的!
一、选择题
1.一个跳水运动员从距离水面10米高的跳台向上跳起0.5米,开始做翻
滚动作,它在空中每完成一个动作需要时间0.2秒,并至少在离水面3.5
米处停止翻滚动作准备入水,最后入水速度为14米/秒,该运动员在空中
至多做翻滚动作( )
A.3个 B.4个 C.5个 D.6个
2.甲、乙两人分别骑车从A、B两地相向而行,甲先行1小时后,乙才出
发,又经过4小时两人在途中的C地相遇,相遇后两人按原来的方向继续
前进.乙在由C地到达A地的途中因故停了20分钟,结果乙由C地到达A
地时比甲由C地到达B地还提前了40分钟,已知乙比甲每小时多行驶4
千米,则甲、乙两人骑车的速度分别为( )千米/时.
A.2,6 B.12,16 C.16,20 D.20,24
二、填空题
3.若两数的和是2,两数的平方和是74,则这两数为________.
4.有一个两位数,它的十位数字与个位数字之和是8,如果把十位数字与
个位数字调换后,所得的两位数乘原来的两位数就得1855,则原来的两
位数是 .
三、解答题
5.(1)有一个两位数等于其数字之积的3倍,其十位数字比个位数字小2,
求这两位数.
(2)两个连续奇数的积是323,求这两个连续奇数.
6.如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P
从A向C运动,点Q同时从C向B运动,速度分别为1cm/s,2cm/s.
当其中一点到达终点时两点同时停止运动.
(1)如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8cm2?
(2)点P、Q在移动过程中,是否存在某一时刻,使得△PCQ的面积等于
△ABC的面积的一半.若存在,求出运动的时间;若不存在,说明理由.
◆测一测,大显身手
1.若两个连续正整数的积为156,则这两个正整数为______.
2.如图所示,已知A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,
动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到点B为止,点Q以2cm/s的速度向D移动.
问:(1)P、Q两点从出发开始到 秒时,四边形PBCQ的面积是33cm2;
(2)P、Q两点从出发开始到 秒时,点P与点O间的距离是10cm.
3.有一个两位数,个位数字与十位数字的和为14,交换数字位置后,得到新的两位数,比这两个数字的积还大38,求这个两位数.
4.已知两个数的和等于12,积等于32,求这两个数是多少.
5.如图所示,AO=OB=50cm,OC是一条射线,OC⊥AB,一只蚂蚁由A点以2cm/s的速度向B爬行,同时另一只蚂蚁由O点以3 cm/s的速度沿OC方向爬行,是否存在这样的时刻,使两只蚂蚁与O点组成的三角形的面积为450cm2
参考答案
试身手, 初露锋芒
练习1、【答案】 x2-5x+6=0.
【提示】本题是结论开放的题(答案不唯一).
练习2、【答案】B
【提示】设这个小组共x人,则x(x-1)=132,x1=-11(舍去),x2=12.
攻难关,自学检测
1.【答案】D
【解析】从10.5米高处到入水过程的平均速度为7米/秒,所用时间为10.5÷7=1.5秒,
速度每秒变化米/秒.设运动员从最高处到离水面3.5米时用时x秒,
那么这段距离的平均速度为x2=1.5,x≈1.2,1.2÷0.2=6,最多做6个翻滚动作.
2.【答案】C
【解析】设甲的速度为x千米/时,则乙的速度为(x+4)千米/时.
根据题意,得
解之,得x1=16,x2=-2.
经检验:x1=16,x2=-2都是原方程的根,但x2=-2不合题意,舍去.
∴当x=16时,x+4=20.
3.【答案】-5和7
【解析】设两数中一个数为x,则另一个数为2-x.
根据题意得x2+(2-x)2=74,解得x1=-5,x2=7.
当x=-5时,另一个数为7;
当x=7时,另一个数为-5,
所以这两个数为-5和7.
4.【答案】35或53
【解析】设原两位数的十位数字为x,则个位数字是(8-x),由题意得
[10x+(8-x)]·[10(8-x)+x]=1855.
化简得x2-8x+15=0,
解之得:x1=3,x2=5.
经检验,x1=3,x2=5都符合题意.
答:原两位数是35或53.
5.解:(1)设十位数字为a,则个位数字为a+2.
依题意,得:11a+2=3×a×(a+2)
整理,得:3a2-5a-2=0
解之得:a1=2,a2=(不合题意,舍去) .
答:这个两位数为24.
(2)设较小的奇数为:2n-1,则较大的奇数为:2n+1.
依题意,得:(2n-1)(2n+1)=323
整理,得:n2-81=0
解之得:n1= 9,n2=-9(不合题意,舍去).
则2n-1=18-1=17,2n+1=18+1=19.
答:这两个连续奇数为17和19.
6.解:(1)设t秒钟之后△PCQ的面积为8cm2.
依题意,得:S△PCQ=PC·QC= (6-t)× 2t=8
整理,得:t2-6t+8=0
解之得:t1=2, t2=4.
答:P、Q同时出发2秒或4秒后,可使△PCQ的面积为8cm2.
(2)假设存在这样的时刻,
依题意,得:S△PCQ=PC·QC= (6-t)× 2t=S△ABC=×24=12
整理,得:t2-6t+12=0
∵△=(-6)2-4×12=36-48=-12<0
∴方程无实数根.
即不存在这样的时间点使得△PCQ的面积等于△ABC的面积的一半.
测一测,大显身手
1.【答案】12和13
2.【答案】(1)5秒;(2)秒或秒.
【解析】(1)设P、Q两点从出发开始到x秒时,四边形PBCQ的面积是33cm2,
则AP=3x,PB=16-3x,CQ=2x,由梯形的面积公式得,
解得x=5.
答:P、Q两点从出发开始到5秒时,四边形PBCO的面积为33cm2.
(2)设P、Q两点从出发开始到y秒时,点P、点Q间的距离为10cm.
过点Q作QH⊥AB,交AB于H,如答图3所示,
则AP=3y,CQ=2y,PH=16-3y-2y,
根据勾股定理.得(16-3y-2y)2=102-62,化简方程得(16-5y)2=64,
解得,.
答:P、Q两点从出发开始到秒或秒时,点P、点Q间的距离是10cm.
3.【解析】解:设个位数字为x,则十位数字为14-x,两数字之积为x(14-x),
两个数字颠倒后的数为10x+(14-x).
根据题意,得10x+(14-x)-x(14-x)=38.
整理,得x2-5x-24=0,
∴ (x-8)(x+3)=0,∴x1=8,x2=-3.
∵个位上的数字不可能是负数,∴x=-3舍去.
当x=8时,14-x=6,∴原数为68.
答:这个两位数是68.
4.【答案】解:设其中一个数为x,那么另一个数可表示为(12-x),依题意得x(12-x)=32,
整理得x2-12x+32=0
解得 x1=4,x2=8,
当x=4时12-x=8;
当x=8时12-x=4.
所以这两个数是4和8.
5.【答案】解:(1)当蚂蚁在AO段时,设离开A点t s后两只蚂蚁与O点组成的三角形的面积是450cm2.
根据题意,得.
整理得:,
解得t1=10,t2=15.
(2)当蚂蚁爬完AO这段距离用了后,开始由O向B爬行,设从O点开始x s后组成的
三角形的面积是450 cm2,根据题意,得:,
整理得x2+25x-150=0,解得x1=5,x2=-30(舍去).
当x=5时,x+25=30.这时蚂蚁已由A点爬了30s.
答:分别在10s,15s,30s时,两只蚂蚁与O点组成的三角形的面积是450cm2.
同课章节目录
