24.2.1 点和圆的位置关系 学案(含答案)
文档属性
| 名称 | 24.2.1 点和圆的位置关系 学案(含答案) | 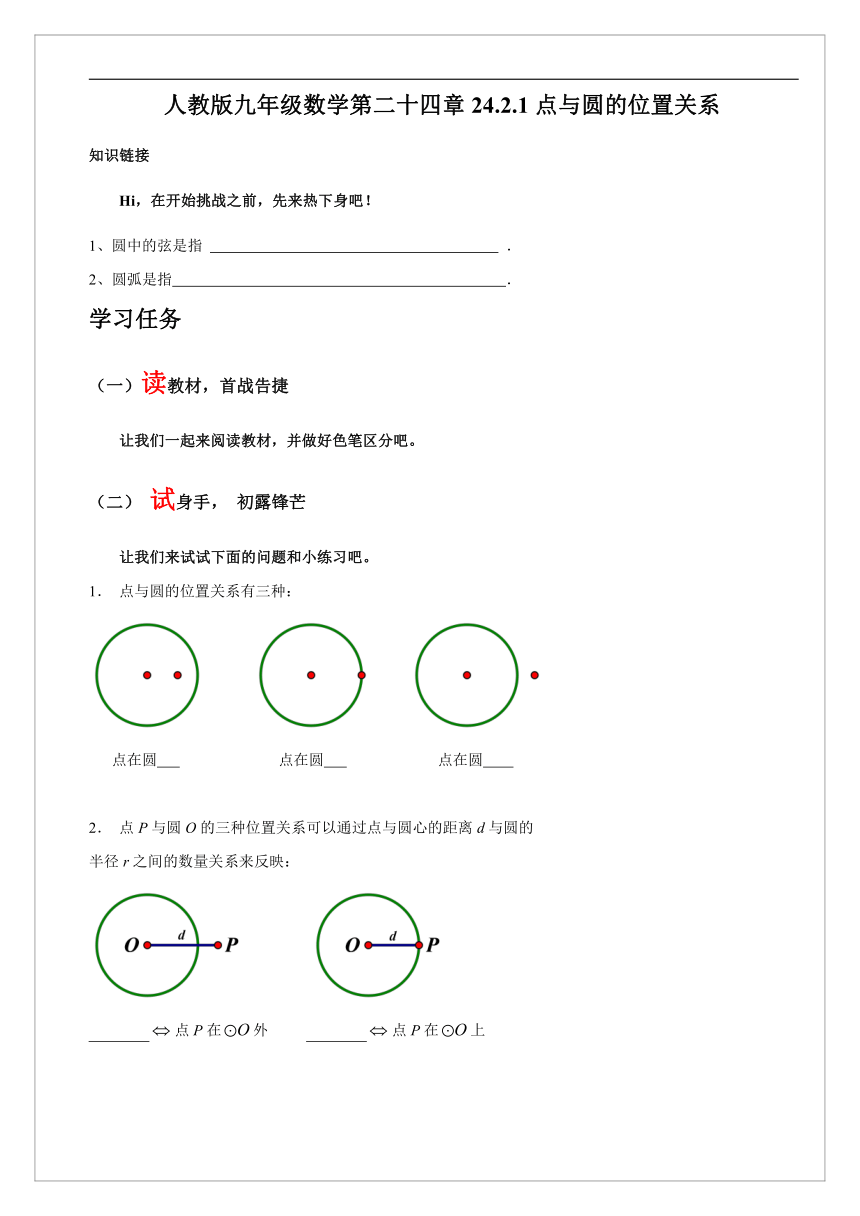 | |
| 格式 | docx | ||
| 文件大小 | 78.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-15 18:05:31 | ||
图片预览




文档简介
人教版九年级数学第二十四章24.2.1点与圆的位置关系
知识链接
Hi,在开始挑战之前,先来热下身吧!
1、圆中的弦是指 .
2、圆弧是指 .
学习任务
(一)读教材,首战告捷
让我们一起来阅读教材,并做好色笔区分吧。
(二) 试身手, 初露锋芒
让我们来试试下面的问题和小练习吧。
1. 点与圆的位置关系有三种:
点在圆 点在圆 点在圆
2. 点P与圆O的三种位置关系可以通过点与圆心的距离d与圆的
半径r之间的数量关系来反映:
点P在外 点P在上
点P在内.
3. 经过点的圆
经过一点的圆有 个;
经过两点的圆有 个,圆心一定在连接这两点线段的 上;
经过同一直线的三点的圆 (存在或不存在) ,
的三个点可以确定一个圆.
4. 经过三角形三个顶点的圆叫做三角形的 ;
三角形的外接圆的圆心叫做三角形的 ;
这个三角形叫做圆的内接三角形.
5. 三角形的外心是三角形三条边的 的交点,它到
三角形 的距离相等.
(三)攻难关,自学检测
让我们来挑战吧!你一定是最棒的!
1. 一个点到圆的最小距离为3cm,最大距离为8cm,则该
圆的半径是( ).
A.5cm或11cm B.2.5dcm C.5.5cm D.2.5cm或5.5cm
2. 已知A为⊙O上的点,⊙O的半径为1,该平面上另有一点P,
,那么点P与⊙O的位置关系是( )
A. 点P在⊙O内 B. 点P在⊙O上
C. 点P在⊙O外 D.无法确定
3. 已知⊙O的半径为5,点A在⊙O外,那么线段OA的取值
范围是 .
4. 的半径为5,圆心O到直线l的距离OD=3,在直线l上
有P、Q、R三点,且有PD=4,QD>4,RD<4,问P、Q、R三点与
的位置关系如何?
练习5. 证明“经过同一直线上的三个点不能作出一个圆”
6. 以点O为圆心,分别以2cm、3cm为半径画两个圆(这两个圆
叫做同心圆),说出满足下列条件的点P的位置:
(1)OP>3cm
(2)OP<2cm
(3)2cm<OP<3cm
(4)OP=0cm.
◆测一测,大显身手
一、选择题
1. 若⊙O的直径为5cm,点A到圆心O的距离为3cm,那么点A与⊙O的位置关系是( )
A. 点A在圆内 B. 点A在圆上
C. 点A在圆外 D.无法确定
2.关于半径为5的圆,下列说法正确的是( )
A.若有一点到圆心的距离为5,则该点在圆外;
B.若有一点在圆外,则该点到圆心的距离不小于5;
C.圆上任意两点之间的线段长度不大于10;
D.圆上任意两点之间的部分可以大于10π;
二、填空题
3. 如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是 .
4. 一个点到定圆上最近点的距离为4,最远点的距离为9,则此圆的半径为 .
三、解答题
5.如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,以A为圆心,3cm为半径作圆.试判断:
(1)点C与⊙A的位置关系;
(2)点B与⊙A的位置关系;
(3)AB的中点D与⊙A的位置关系.
参考答案:
试身手, 初露锋芒
1.内,上,外.
2. d>r,d=r,d<r.
3. 无数,无数,垂直平分线,不存在,不在同一条直线上.
4. 外接圆,外心.
5. 垂直平分线,三个顶点.
攻难关,自学检测
1. D.
2. D.
3. OA>5
4. 解:(1)由勾股定理,可知:
P为直线l与的交点,即点P在上.
第二行最后一个是圆心角.理由:与圆心角概念一致.
(2)由勾股定理,可知:
P为直线l与的交点,即点P在上.
OR<5,所以点R在内部.
OQ>5,所以点Q在外部.
5. 证明:假设经过直线l上的ABC三个点可以作一个圆P,
则P在AB的垂直平分线上l1,P也在BC的垂直平分线l2上.
则l1和l2相交于点P.
而,
这与过一点有且只有一条直线和已知直线垂直矛盾
所以,假设不成立,故经过同一直线上的三个点不能作出一个圆.
6. 解:(1)∵OP>3cm,
∴点P此时在大圆外;
(2)∵OP<2cm,
∴此时点P在小圆内;
(3)∵2cm<OP<3cm,
∴此时点P在两圆组成的圆环内;
(4)∵OP=0cm,
∴点P为同心圆的圆心.
测一测,大显身手
1. A;
2. C;
3. 3<r<5;
4. 6.5或2.5.
5. 解:∵∠C=90°,AB=5cm,BC=4cm,
∴AC=3cm,BA=5cm,DA=2.5cm,
(1)∵AC=r=3cm,∴点C在⊙A上;
(2)∵BA=5cm>3cm,∴BA>r,∴点B在⊙A外;
(3)∵DA=2.5cm<3cm,∴DA<r,∴点D在⊙A内.
知识链接
Hi,在开始挑战之前,先来热下身吧!
1、圆中的弦是指 .
2、圆弧是指 .
学习任务
(一)读教材,首战告捷
让我们一起来阅读教材,并做好色笔区分吧。
(二) 试身手, 初露锋芒
让我们来试试下面的问题和小练习吧。
1. 点与圆的位置关系有三种:
点在圆 点在圆 点在圆
2. 点P与圆O的三种位置关系可以通过点与圆心的距离d与圆的
半径r之间的数量关系来反映:
点P在外 点P在上
点P在内.
3. 经过点的圆
经过一点的圆有 个;
经过两点的圆有 个,圆心一定在连接这两点线段的 上;
经过同一直线的三点的圆 (存在或不存在) ,
的三个点可以确定一个圆.
4. 经过三角形三个顶点的圆叫做三角形的 ;
三角形的外接圆的圆心叫做三角形的 ;
这个三角形叫做圆的内接三角形.
5. 三角形的外心是三角形三条边的 的交点,它到
三角形 的距离相等.
(三)攻难关,自学检测
让我们来挑战吧!你一定是最棒的!
1. 一个点到圆的最小距离为3cm,最大距离为8cm,则该
圆的半径是( ).
A.5cm或11cm B.2.5dcm C.5.5cm D.2.5cm或5.5cm
2. 已知A为⊙O上的点,⊙O的半径为1,该平面上另有一点P,
,那么点P与⊙O的位置关系是( )
A. 点P在⊙O内 B. 点P在⊙O上
C. 点P在⊙O外 D.无法确定
3. 已知⊙O的半径为5,点A在⊙O外,那么线段OA的取值
范围是 .
4. 的半径为5,圆心O到直线l的距离OD=3,在直线l上
有P、Q、R三点,且有PD=4,QD>4,RD<4,问P、Q、R三点与
的位置关系如何?
练习5. 证明“经过同一直线上的三个点不能作出一个圆”
6. 以点O为圆心,分别以2cm、3cm为半径画两个圆(这两个圆
叫做同心圆),说出满足下列条件的点P的位置:
(1)OP>3cm
(2)OP<2cm
(3)2cm<OP<3cm
(4)OP=0cm.
◆测一测,大显身手
一、选择题
1. 若⊙O的直径为5cm,点A到圆心O的距离为3cm,那么点A与⊙O的位置关系是( )
A. 点A在圆内 B. 点A在圆上
C. 点A在圆外 D.无法确定
2.关于半径为5的圆,下列说法正确的是( )
A.若有一点到圆心的距离为5,则该点在圆外;
B.若有一点在圆外,则该点到圆心的距离不小于5;
C.圆上任意两点之间的线段长度不大于10;
D.圆上任意两点之间的部分可以大于10π;
二、填空题
3. 如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是 .
4. 一个点到定圆上最近点的距离为4,最远点的距离为9,则此圆的半径为 .
三、解答题
5.如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,以A为圆心,3cm为半径作圆.试判断:
(1)点C与⊙A的位置关系;
(2)点B与⊙A的位置关系;
(3)AB的中点D与⊙A的位置关系.
参考答案:
试身手, 初露锋芒
1.内,上,外.
2. d>r,d=r,d<r.
3. 无数,无数,垂直平分线,不存在,不在同一条直线上.
4. 外接圆,外心.
5. 垂直平分线,三个顶点.
攻难关,自学检测
1. D.
2. D.
3. OA>5
4. 解:(1)由勾股定理,可知:
P为直线l与的交点,即点P在上.
第二行最后一个是圆心角.理由:与圆心角概念一致.
(2)由勾股定理,可知:
P为直线l与的交点,即点P在上.
OR<5,所以点R在内部.
OQ>5,所以点Q在外部.
5. 证明:假设经过直线l上的ABC三个点可以作一个圆P,
则P在AB的垂直平分线上l1,P也在BC的垂直平分线l2上.
则l1和l2相交于点P.
而,
这与过一点有且只有一条直线和已知直线垂直矛盾
所以,假设不成立,故经过同一直线上的三个点不能作出一个圆.
6. 解:(1)∵OP>3cm,
∴点P此时在大圆外;
(2)∵OP<2cm,
∴此时点P在小圆内;
(3)∵2cm<OP<3cm,
∴此时点P在两圆组成的圆环内;
(4)∵OP=0cm,
∴点P为同心圆的圆心.
测一测,大显身手
1. A;
2. C;
3. 3<r<5;
4. 6.5或2.5.
5. 解:∵∠C=90°,AB=5cm,BC=4cm,
∴AC=3cm,BA=5cm,DA=2.5cm,
(1)∵AC=r=3cm,∴点C在⊙A上;
(2)∵BA=5cm>3cm,∴BA>r,∴点B在⊙A外;
(3)∵DA=2.5cm<3cm,∴DA<r,∴点D在⊙A内.
同课章节目录
