24.3 正多边形和圆 学案(含答案)
文档属性
| 名称 | 24.3 正多边形和圆 学案(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 270.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-15 00:00:00 | ||
图片预览

文档简介
人教版九年级数学第二十四章24.3正多边形和圆
知识链接
Hi,在开始挑战之前,先来热下身吧!
1、切线的性质定理: .
2、切线的判定定理: .
学习任务
(一)读教材,首战告捷
让我们一起来阅读教材,并做好色笔区分吧。
(二) 试身手, 初露锋芒
让我们来试试下面的问题和小练习吧。
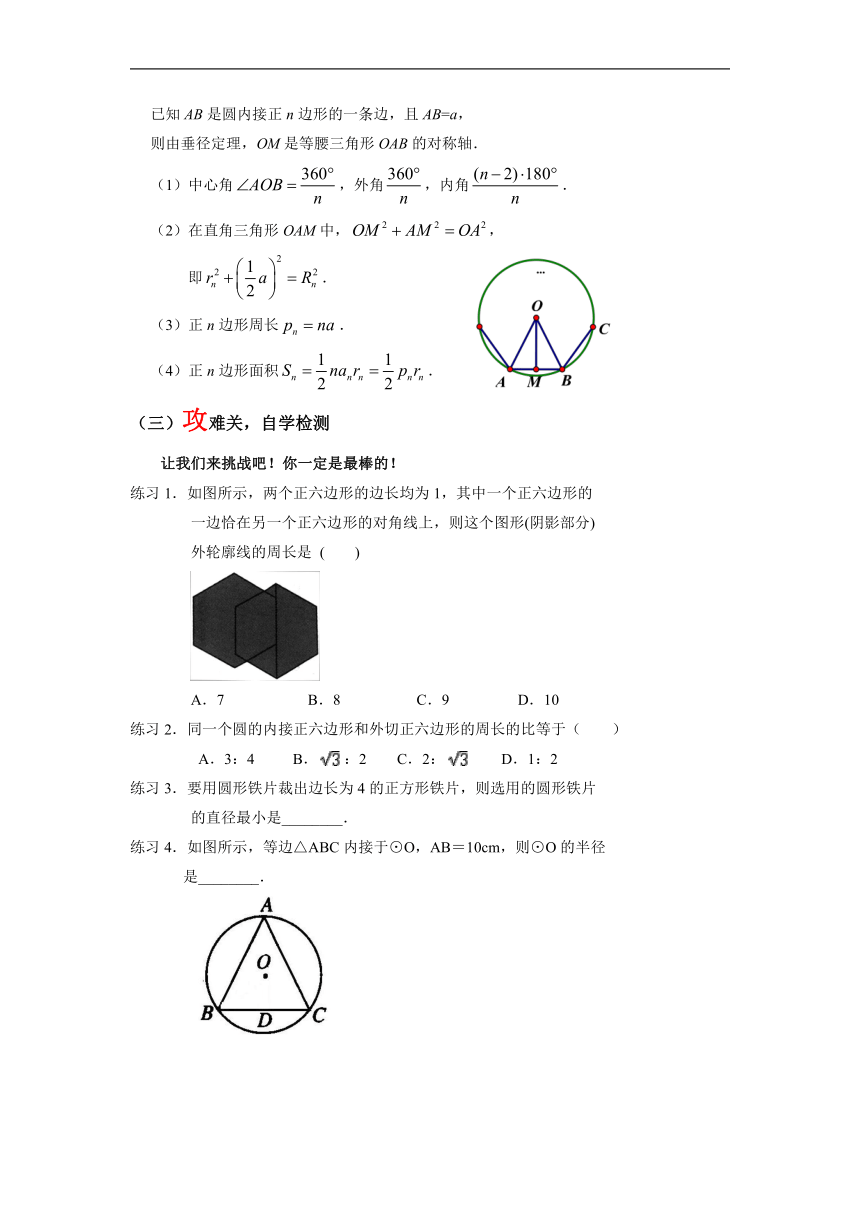
1.各边 ,各角 的多边形叫正多边形.
如图,把一个圆作n等分(n≥3,n是正整数),就可以作出这个
圆的 正n边形,这个圆就是这个正n边形的外接圆.
2.填表
点O 正多边形的 圆心
线段OA 正多边形的 圆的半径
AOB 正多边形的 圆心角
O到AB的距离OM 正多边形的 弦心距
3.正多边形的有关结论
已知AB是圆内接正n边形的一条边,且AB=a,
则由垂径定理,OM是等腰三角形OAB的对称轴.
(1)中心角,外角,内角.
(2)在直角三角形OAM中,,
即.
(3)正n边形周长.
(4)正n边形面积.
(三)攻难关,自学检测
让我们来挑战吧!你一定是最棒的!
练习1.如图所示,两个正六边形的边长均为1,其中一个正六边形的
一边恰在另一个正六边形的对角线上,则这个图形(阴影部分)
外轮廓线的周长是 ( )
A.7 B.8 C.9 D.10
练习2.同一个圆的内接正六边形和外切正六边形的周长的比等于( )
A.3:4 B.:2 C.2: D.1:2
练习3.要用圆形铁片裁出边长为4的正方形铁片,则选用的圆形铁片
的直径最小是________.
练习4.如图所示,等边△ABC内接于⊙O,AB=10cm,则⊙O的半径
是________.
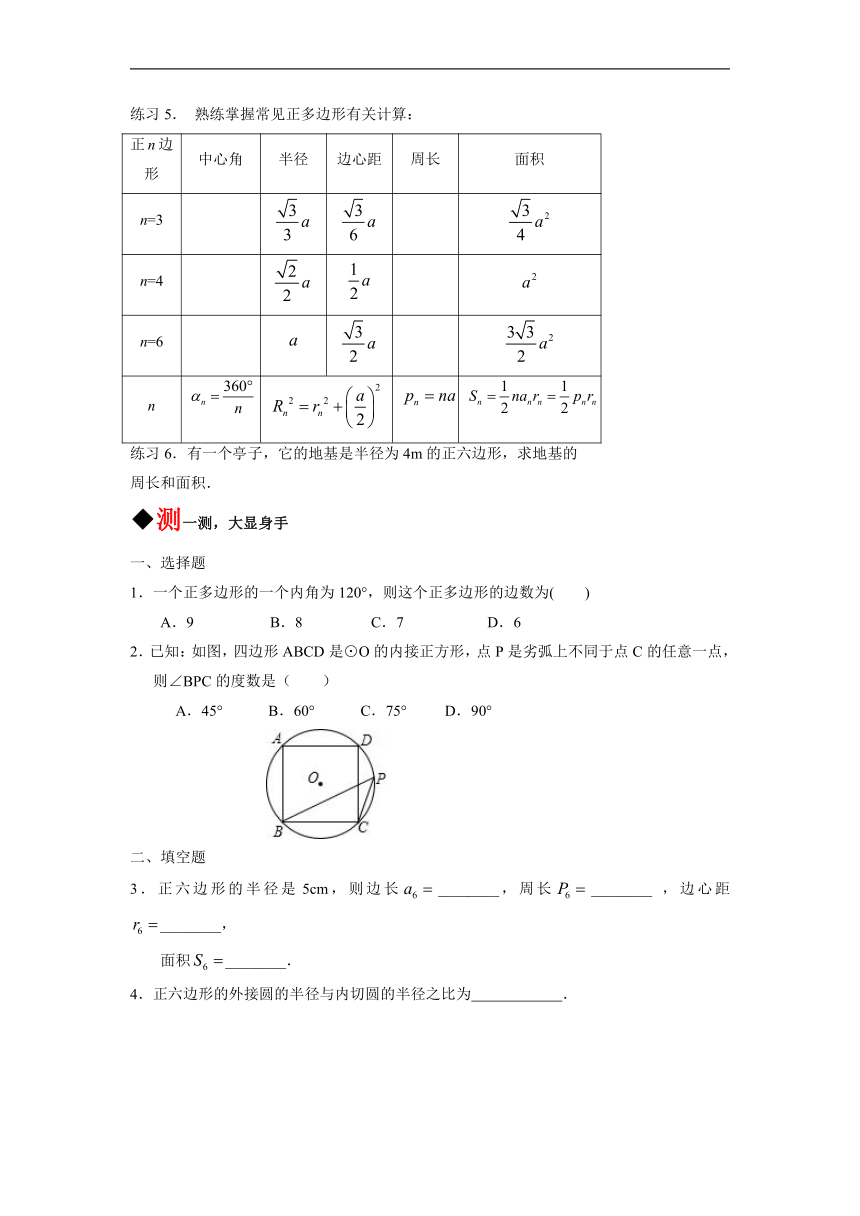
练习5. 熟练掌握常见正多边形有关计算:
正n边形 中心角 半径 边心距 周长 面积
n=3
n=4
n=6
n
练习6.有一个亭子,它的地基是半径为4m的正六边形,求地基的
周长和面积.
◆测一测,大显身手
一、选择题
1.一个正多边形的一个内角为120°,则这个正多边形的边数为( )
A.9 B.8 C.7 D.6
2.已知:如图,四边形ABCD是⊙O的内接正方形,点P是劣弧上不同于点C的任意一点,则∠BPC的度数是( )
A.45° B.60° C.75° D.90°
二、填空题
3.正六边形的半径是5cm,则边长________,周长________ ,边心距________,
面积________.
4.正六边形的外接圆的半径与内切圆的半径之比为 .
三、解答题
5.如图所示,正△ABC的外接圆的圆心为O,半径为2,求△ABC的边长a,周长P,边心距r,面积S.
参考答案:
试身手, 初露锋芒
1.相等,也相等,内接.
2.中心,半径,中心角,边心距.
攻难关,自学检测
1. B.
2. B.
3. ;
提示:如图所示,△ABC为等腰Rt△,.
4. cm;
提示:过O作OD⊥BC于D,连接OB,在Rt△BOD中,BD=BC==5(cm).
∠BOD=,
∴ .
∴ BO=(cm).
5.中心角:120°, 周长:3a
90°, 4a
60°, 6a
6.解:如图,正六边形ABCDEF,连接OB,OC.
∴,
∴是等边三角形.
∴.
∴周长=(m).
面积=(m2).
测一测,大显身手
1. D
2. A
3. 5cm,30cm,cm,
4. 2:
提示:设正六边形的半径是r,则外接圆的半径r,
内切圆的半径是正六边形的边心距,因而是,
因而正六边形的外接圆的半径与内切圆的半径之比为2:.
5.解: 作AD⊥BC于D.
∵ △ABC是正三角形,
∴ 点O在AD上,a=BC=2CD,∠OCD=30°,
在Rt△COD中,,
,
∴ ,.
又∵ AD=OA+OD=2+1=3,
∴ ,
∴ ,,,.
知识链接
Hi,在开始挑战之前,先来热下身吧!
1、切线的性质定理: .
2、切线的判定定理: .
学习任务
(一)读教材,首战告捷
让我们一起来阅读教材,并做好色笔区分吧。
(二) 试身手, 初露锋芒
让我们来试试下面的问题和小练习吧。
1.各边 ,各角 的多边形叫正多边形.
如图,把一个圆作n等分(n≥3,n是正整数),就可以作出这个
圆的 正n边形,这个圆就是这个正n边形的外接圆.
2.填表
点O 正多边形的 圆心
线段OA 正多边形的 圆的半径
AOB 正多边形的 圆心角
O到AB的距离OM 正多边形的 弦心距
3.正多边形的有关结论
已知AB是圆内接正n边形的一条边,且AB=a,
则由垂径定理,OM是等腰三角形OAB的对称轴.
(1)中心角,外角,内角.
(2)在直角三角形OAM中,,
即.
(3)正n边形周长.
(4)正n边形面积.
(三)攻难关,自学检测
让我们来挑战吧!你一定是最棒的!
练习1.如图所示,两个正六边形的边长均为1,其中一个正六边形的
一边恰在另一个正六边形的对角线上,则这个图形(阴影部分)
外轮廓线的周长是 ( )
A.7 B.8 C.9 D.10
练习2.同一个圆的内接正六边形和外切正六边形的周长的比等于( )
A.3:4 B.:2 C.2: D.1:2
练习3.要用圆形铁片裁出边长为4的正方形铁片,则选用的圆形铁片
的直径最小是________.
练习4.如图所示,等边△ABC内接于⊙O,AB=10cm,则⊙O的半径
是________.
练习5. 熟练掌握常见正多边形有关计算:
正n边形 中心角 半径 边心距 周长 面积
n=3
n=4
n=6
n
练习6.有一个亭子,它的地基是半径为4m的正六边形,求地基的
周长和面积.
◆测一测,大显身手
一、选择题
1.一个正多边形的一个内角为120°,则这个正多边形的边数为( )
A.9 B.8 C.7 D.6
2.已知:如图,四边形ABCD是⊙O的内接正方形,点P是劣弧上不同于点C的任意一点,则∠BPC的度数是( )
A.45° B.60° C.75° D.90°
二、填空题
3.正六边形的半径是5cm,则边长________,周长________ ,边心距________,
面积________.
4.正六边形的外接圆的半径与内切圆的半径之比为 .
三、解答题
5.如图所示,正△ABC的外接圆的圆心为O,半径为2,求△ABC的边长a,周长P,边心距r,面积S.
参考答案:
试身手, 初露锋芒
1.相等,也相等,内接.
2.中心,半径,中心角,边心距.
攻难关,自学检测
1. B.
2. B.
3. ;
提示:如图所示,△ABC为等腰Rt△,.
4. cm;
提示:过O作OD⊥BC于D,连接OB,在Rt△BOD中,BD=BC==5(cm).
∠BOD=,
∴ .
∴ BO=(cm).
5.中心角:120°, 周长:3a
90°, 4a
60°, 6a
6.解:如图,正六边形ABCDEF,连接OB,OC.
∴,
∴是等边三角形.
∴.
∴周长=(m).
面积=(m2).
测一测,大显身手
1. D
2. A
3. 5cm,30cm,cm,
4. 2:
提示:设正六边形的半径是r,则外接圆的半径r,
内切圆的半径是正六边形的边心距,因而是,
因而正六边形的外接圆的半径与内切圆的半径之比为2:.
5.解: 作AD⊥BC于D.
∵ △ABC是正三角形,
∴ 点O在AD上,a=BC=2CD,∠OCD=30°,
在Rt△COD中,,
,
∴ ,.
又∵ AD=OA+OD=2+1=3,
∴ ,
∴ ,,,.
同课章节目录
