2022-2023学年苏科版九年级数学上册第2章对称图形——圆 解答题专题训练(word、含答案)
文档属性
| 名称 | 2022-2023学年苏科版九年级数学上册第2章对称图形——圆 解答题专题训练(word、含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-17 00:00:00 | ||
图片预览



文档简介
2022-2023学年苏科版九年级数学上册《第2章对称图形——圆》解答题专题训练(附答案)
1.如图,AB是⊙O的直径,点C在⊙O上,=,点D是的中点,连结OC,AD,交于点E,连结BE,BD.
(1)求∠EBA的度数.
(2)求证:AE=BD.
(3)若DE=1,求⊙O的面积.
2.如图,在⊙O中,AC为⊙O的直径,AB为⊙O的弦,点E是的中点,过点E作AB的垂线,交AB于点M,交⊙O于点N,分别连接EB,CN.
(1)EM与BE的数量关系是 ;
(2)求证:=;
(3)若AM=,MB=2,求阴影部分图形的面积.
3.如图,Rt△ABC中,∠C=90°,点O在AC上,以OA为半径的半圆O分别交AB,AC于点D,E,过点D作半圆O的切线DF,交BC于点F.
(1)求证:BF=DF;
(2)若AO=CE=4,CF=1,求BF的长.
4.如图,在△ABC中,以AB为直径的⊙O交AC于点D,过点D作⊙O的切线,交BC于点E,连接BD.
(1)判断∠ABD与∠CDE的数量关系,并说明理由.
(2)若∠EDB=40°,OB=4,求的长.
5.如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,OE⊥AB于点H,连接CE,过点C作⊙O的切线交AB的延长线于点D.
(1)求证:∠COE=2∠DCE;
(2)若AB=8,EH=2,求BD的长.
6.如图,△ABC内接于⊙O,∠ACB=45°,AD是⊙O的直径,过点B作AD的平行线,交AC的延长线于点P.
(1)求证:PB是⊙O的切线;
(2)若AB=2,∠CAB=30°,则的长为 .(结果保留π)
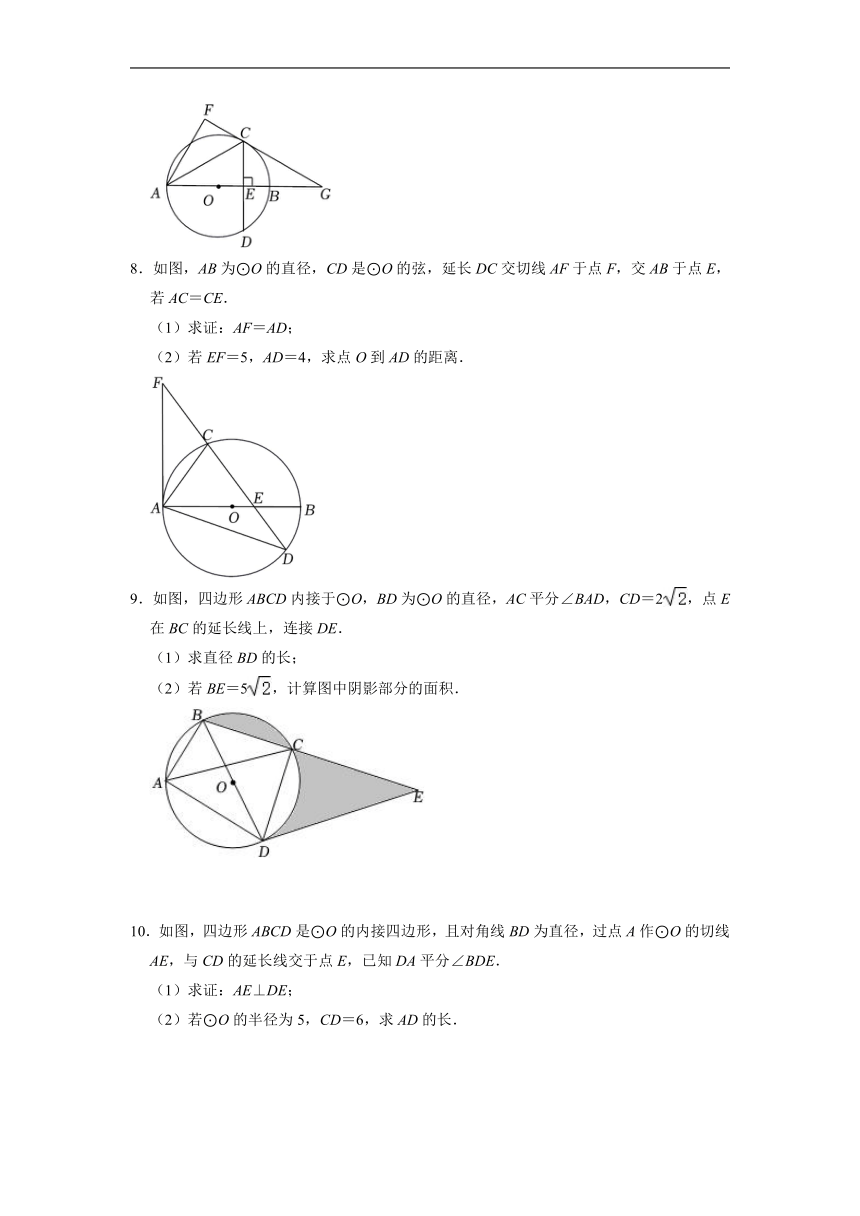
7.如图,在⊙O中,直径AB垂直于弦CD,垂足为E,连接AC,将△ACE沿AC翻折得到△ACF,直线FC与直线AB相交于点G.
(1)直线FC与⊙O有何位置关系?并说明理由;
(2)若OB=GB=2,求GF的长.
8.如图,AB为⊙O的直径,CD是⊙O的弦,延长DC交切线AF于点F,交AB于点E,若AC=CE.
(1)求证:AF=AD;
(2)若EF=5,AD=4,求点O到AD的距离.
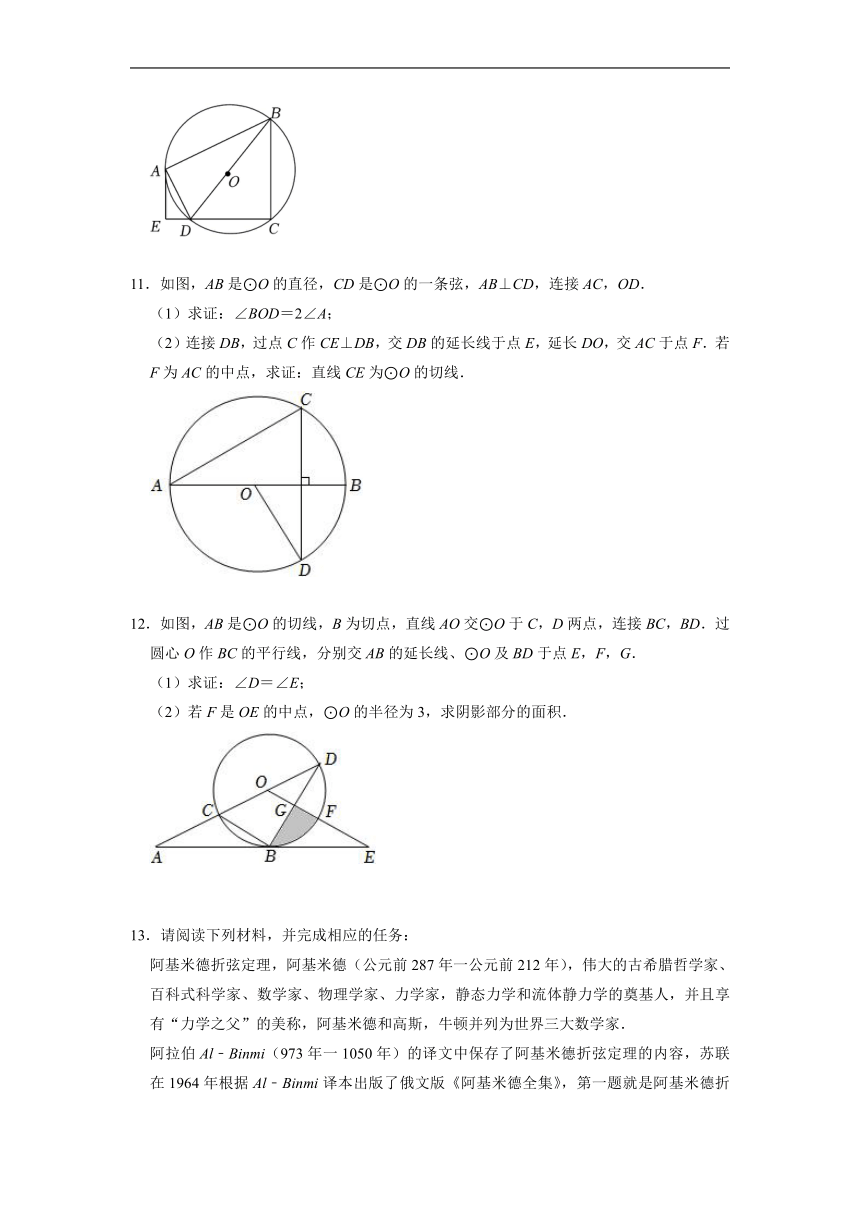
9.如图,四边形ABCD内接于⊙O,BD为⊙O的直径,AC平分∠BAD,CD=2,点E在BC的延长线上,连接DE.
(1)求直径BD的长;
(2)若BE=5,计算图中阴影部分的面积.
10.如图,四边形ABCD是⊙O的内接四边形,且对角线BD为直径,过点A作⊙O的切线AE,与CD的延长线交于点E,已知DA平分∠BDE.
(1)求证:AE⊥DE;
(2)若⊙O的半径为5,CD=6,求AD的长.
11.如图,AB是⊙O的直径,CD是⊙O的一条弦,AB⊥CD,连接AC,OD.
(1)求证:∠BOD=2∠A;
(2)连接DB,过点C作CE⊥DB,交DB的延长线于点E,延长DO,交AC于点F.若F为AC的中点,求证:直线CE为⊙O的切线.
12.如图,AB是⊙O的切线,B为切点,直线AO交⊙O于C,D两点,连接BC,BD.过圆心O作BC的平行线,分别交AB的延长线、⊙O及BD于点E,F,G.
(1)求证:∠D=∠E;
(2)若F是OE的中点,⊙O的半径为3,求阴影部分的面积.
13.请阅读下列材料,并完成相应的任务:
阿基米德折弦定理,阿基米德(公元前287年一公元前212年),伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家,静态力学和流体静力学的奠基人,并且享有“力学之父”的美称,阿基米德和高斯,牛顿并列为世界三大数学家.
阿拉伯Al﹣Binmi(973年一1050年)的译文中保存了阿基米德折弦定理的内容,苏联在1964年根据Al﹣Binmi译本出版了俄文版《阿基米德全集》,第一题就是阿基米德折弦定理.
阿基米德折弦定理:如图1,AB和BC是⊙O的两条弦(即折线ABC是圆的一条折弦),BC>AB,M是的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=AB+BD.
小明同学运用“截长法”和三角形全等来证明CD=AB+BD,过程如下:
证明:如图2所示,在CB上截取CG=AB,连接MA,MB,MC和MG.
∵M是的中点,∴MA=MC,…
任务:
(1)请按照上述思路,写出该证明的剩余部分;
(2)如图3,已知等边△ABC内接于⊙O,AB=4,D为上一点,∠ABD=45°,AE⊥BD于点E,请直接写出△BDC的周长.
14.如图1,AB是⊙O的直径,点F是⊙O上的一点,连接AF,过点O作OC∥AF交⊙O于点C,过点C作⊙O的切线,交FA的延长线于点D,CE⊥AB于E,连接AC.
(1)求证:AD=AE;
(2)如图2,在图1的条件下,若点F为半圆的中点,连接CF交AB于点M,求∠AMC的度数.
15.如图,△ABC内接于⊙O,AD∥BC交⊙O于点D,DF∥AB交BC于点E,交⊙O于点F,连接AF,CF.
(1)求证:AC=AF;
(2)若⊙O的半径为3,∠CAF=30°,求的长(结果保留π).
16.如图,D是△ABC的BC边上一点,连结AD,作△ABD的外接圆O,将△ADC沿直线AD折叠,点C的对应点E落在⊙O上.
(1)若∠ABC=30°,如图1.
①求∠ACB的度数.
②若AD=DE,求∠EAB的度数.
(2)若,如图2.求BC的长.
17.如图,在⊙O中,AB,AC为弦,CD为直径,AB⊥CD于E,BF⊥AC于F,BF与CD相交于G.
(1)求证:ED=EG;
(2)若AB=8,OG=1,求⊙O的半径.
18.石拱桥是我国古代人民勤劳和智慧的结晶(如图1),隋代建造的赵州桥距今约有1400年历史,是我国古代石拱桥的代表.如图2是根据某石拱桥的实物图画出的几何图形,桥的主桥拱是圆弧形,表示为.桥的跨度(弧所对的弦长)AB=26m,设所在圆的圆心为O,半径OC⊥AB,垂足为D.拱高(弧的中点到弦的距离)CD=5m.连接OB.
(1)直接判断AD与BD的数量关系;
(2)求这座石拱桥主桥拱的半径(精确到1m).
19.如图,以AB为直径的⊙O经过△ABC的顶点C,AE,BE分别平分∠BAC和∠ABC,AE的延长线交⊙O于点D,连接BD.
(1)判断△BDE的形状,并证明你的结论;
(2)若AB=10,BE=2,求BC的长.
20.如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作⊙O的切线与BC的延长线交于F.
(1)如图1,求证:四边形DBFP为矩形;
(2)如图2,连接DF交AC于E,连接PE,判断PE与AC的位置关系,并证明你的结论.
参考答案
1.解:(1)连接AC,
∵=,
∴∠AOC=∠BOC=90°
∴∠CAB=45°,
∵点D是的中点,
∴,
∴∠CAD=∠EAB=22.5°;
(2)由(1)知,OC垂直平分AB,
∴AE=BE,
∴∠DEB=2∠EAB=45°,
∵AB是直径,
∴∠D=90°,
∴BD=sin45°BE,
∴BE=BD,
∴AE=BD;
(3)∵DE=1
∴BD=DE=1,
∴AE=BE=,
∴AD=+1,
在Rt△ABD中,AD2+BD2=(2OA)2,
∴()2+1=4OA2,
∴OA2=,
∴圆的面积为πOA2=.
2.(1)解:结论:BE=EM.
理由:∵AC为⊙O的直径,点E是的中点,
∴∠ABE=45°,
∵AB⊥EN,
∴△BME是等腰直角三角形,
∴BE=EM,
故答案为:BE=EM;
(2)证明:连接EO,
∵AC是⊙O的直径,E是的中点,
∴∠AOE=90°,
∴∠ABE=∠AOE=45°,
∵EN⊥AB,垂足为点M,
∴∠EMB=90°
∴∠ABE=∠BEN=45°,
∴=,
∵点E是的中点,
∴=,
∴=,
∴﹣=﹣,
∴=;
(3)解:连接AE,OB,ON,
∵EN⊥AB,垂足为点M,
∴∠AME=∠EMB=90°,
∵BM=1,由(2)得∠ABE=∠BEN=45°,
∴EM=BM=2,
又∵BE=EM,
∴BE=2,
∵在Rt△AEM中,EM=2,AM=2,
∴∠EAB=30°,
∵∠EAB=∠EOB,
∴∠EOB=60°,
又∵OE=OB,
∴△EOB是等边三角形,
∴OE=BE=2,
又∵=,
∴BE=CN,
∴△OEB≌△OCN(SSS),
∴CN=BE=2
又∵S扇形OCN==π,S△OCN= CN×CN=×2××2=2,
∴S阴影=S扇形OCN﹣S△OCN=π﹣2.
3.(1)证明:连接OD,
∵∠C=90°,
∴∠A+∠B=90°,
∵DF与半⊙O相切于点D,
∴∠ODF=90°,
∴∠ADO+∠BDF=180°﹣∠ODF=90°,
∵OA=OD,
∴∠A=∠ADO,
∴∠B=∠BDF,
∴BF=DF;
(2)解:连接OF,
∵∠C=90°,OC=OE+CE=8,CF=1,
∴OF2=OC2+CF2=82+12=65,
在Rt△ODF中,OD=AO=4,
∴DF====7,
∴DF=BF=7,
∴BF的长为7.
4.解:(1)∠ABD=∠CDE.
证明:连接OD,如图,
∵DE为切线,
∴OD⊥DE,
∴∠ODB+∠BDE=90°,
∵AB为直径,
∴∠ADB=90°,
∴∠CDE+∠BDE=90°,
∴∠ODB=∠CDE,
∵OB=OD,
∴∠ABD=∠ODB,
∴∠ABD=∠CDE;
(2)∵∠EDB=40°,∠ODE=90°,
∴∠ODB=90°﹣∠EDB=90°﹣40°=50°,
∵OD=OB,
∴∠ODB=∠OBD,
∴∠BOD=80°,
∵OB=4,
∴的长==.
5.(1)证明:连接AE,如图,
∵CD为⊙O的切线,
∴AC⊥CD,
∴∠ACD=90°,
即∠ACE+∠DCE=90°,
∵AC是⊙O的直径,
∴∠AEC=90°,
∴∠ACE+∠CAE=90°,
∴∠CAE=∠DCE,
∵∠COE=2∠CAE,
∴∠COE=2∠DCE;
(2)解:∵OE⊥AB,
∴AH=BH=AB=4,
设⊙O的半径为r,则OH=r﹣2,OA=r,
在Rt△AOH中,42+(r﹣2)2=r2,
解得r=5,
∴AC=2r=10,
∵∠CAB=∠DAC,∠ABC=∠ACD,
∴AC:AB=AD:AC,即10:8=AD:10,
解得AD=,
∴BD=AD﹣AB=﹣8=.
6.(1)证明:连接OB,
∵∠ACB=45°,
∴∠AOB=2∠ACB=90°,
∵AD∥BP,
∴∠AOB=∠OBP=90°,
∵OB是⊙O的半径,
∴PB是⊙O的切线;
(2)解:连接OC,
∵∠AOB=90°,OA=BO,AB=2,
∴OA=OB==,
∵∠CAB=30°,
∴∠COB=2∠CAB=60°,
∴的长==,
故答案为:.
7.解:(1)FG是⊙O的切线;
理由:连接OC,如图,
∵OA=OC,
∴∠OAC=∠OCA,
∵△ACE沿AC翻折得到△ACF,
∴∠OAC=∠FAC,∠F=∠AEC=90°,
∴∠OCA=∠FAC,
∴OC∥AF,
∴∠OCG=∠F=90°,
∴OC⊥FG,
∵OC是⊙O的半径,
∴直线FC与⊙O相切;
(2)∵OB=GB=OC=2,∠OCG=90°,
∴OC=OG,
∴∠G=30°,AG=6,
∵∠F=90°,
∴FG=AG=3.
8.(1)证明:连接BC,
∵CA=CE,
∴∠CAE=∠CEA,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAE+∠B=90°,
∵AF与⊙O相切于点A,
∴∠BAF=90°,
∴∠AEC+∠F=90°,
∴∠F=∠B,
∵∠B=∠D,
∴∠D=∠F,
∴AF=AD;
(2)解:连接BD,过点O作OH⊥AB,垂足为H,
∴AH=DH,
∵OA=OB,
∴OH是△ABD的中位线,
∴OH=BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
在Rt△AFE中,FE=5,AF=AD=4,
∴AE===3,
∵∠F+∠AEF=90°,∠FAC+∠CAE=90°,∠AEF=∠CAE,
∴∠F=∠FAC,
∴CF=AC,
∵AC=CE,
∴AC=CF=CE=EF=2.5,
∵∠CAE=∠CDB,∠CEA=∠BED,
∴∠BED=∠CDB,
∴BE=BD,
设BE=BD=x,
∴AB=AE+BE=3+x,
在Rt△ABD中,AD2+BD2=AB2,
∴16+x2=(3+x)2,
∴x=,
∴BD=,
∴OH=BD=,
∴点O到AD的距离为.
9.解:(1)∵BD为⊙O的直径,
∴∠BCD=∠DCE=90°,
∵AC平分∠BAD,
∴∠BAC=∠DAC,
∴BC=DC=2,
∴BD=2×=4;
(2)∵BE=5,
∴CE=3,
∵BC=DC,
∴S阴影=S△CDE=×2×=6.
10.(1)证明:连接OA,
∵AE是⊙O的切线,
∴∠OAE=90°,
∵OA=OD,
∴∠OAD=∠ODA,
∵DA平分∠BDE,
∴∠ODA=∠ADE,
∴∠ADE=∠OAD,
∴OA∥CE,
∴∠E=180°﹣∠OAE=90°,
∴AE⊥DE;
(2)解:过点O作OF⊥DC,垂足为F,
∴∠OFD=90°,
∵∠OAE=∠E=90°,
∴四边形OAEF是矩形,
∴OA=EF=5,AE=OF,
∵OF⊥CD,
∴DF=CD=3,
∴DE=EF﹣DF=5﹣3=2,
∴OF===4,
∵AE=OF=4,
∴AD===2,
∴AD的长为2.
11.证明:(1)如图,连接AD,
∵AB是⊙O的直径,AB⊥CD,
∴,
∴∠CAB=∠BAD,
∵∠BOD=2∠BAD,
∴∠BOD=2∠A;
(2)如图,连接OC,
∵F为AC的中点,
∴DF⊥AC,
∴AD=CD,
∴∠ADF=∠CDF,
∵,
∴∠CAB=∠DAB,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠CDF=∠CAB,
∵OC=OD,
∴∠CDF=∠OCD,
∴∠OCD=∠CAB,
∵,
∴∠CAB=∠CDE,
∴∠CDE=∠OCD,
∵∠E=90°,
∴∠CDE+∠DCE=90°,
∴∠OCD+∠DCE=90°,
即OC⊥CE,
∵OC为半径,
∴直线CE为⊙O的切线.
12.(1)证明:连接OB,
∵AB是⊙O的切线,
∴∠OBE=90°,
∴∠E+∠BOE=90°,
∵CD为⊙O的直径,
∴∠CBD=90°,
∴∠D+∠DCB=90°,
∵OE∥BC,
∴∠BOE=∠OBC,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠BOE=∠OCB,
∴∠D=∠E;
(2)解:∵F为OE的中点,OB=OF,
∴OF=EF=3,
∴OE=6,
∴BO=OE,
∵∠OBE=90°,
∴∠E=30°,
∴∠BOG=60°,
∵OE∥BC,∠DBC=90°,
∴∠OGB=90°,
∴OG=,BG=,
∴S△BOG=OG BG==,S扇形BOF==π,
∴S阴影部分=S扇形BOF﹣S△BOG=.
13.解:(1)∵
∴∠A=∠C,
∵M是的中点,
∴MA=MC,
在△MBA≌△MCG中,
,
∴△MBA≌△MCG(SAS),
∴MB=MG,
∵MD⊥BC,
∴BD=GD,
∴CG+GD=AB+BD,
即CD=AB+BD;
(2)∵△ABC是等边三角形,
∴AB=AC,
∴,
由阿基米德折弦定理,可得BE=ED+DC,
∵∠ABD=45°,AB=4,∠AEB=90°,
∴BE=AB=2,
故△BDC的周长为:BC+BD+CD=BC+BE+ED+DC=BC+2BE=4+4.
14.(1)证明:∵CD是⊙O的切线,
∴OC⊥CD,
∴∠DCA+∠OCA=90°.
∵OC=OA,
∴∠OCA=∠OAC.
∴∠OAC+∠DCA=90°.
∵CE⊥AB,
∴∠OAC+∠ECA=90°.
∴∠DCA=∠ECA.
∵OC∥AF,OC⊥CD,
∴CD⊥AF,
∴∠D=90°.
在△DAC和△EAC中,
,
∴△DAC≌△EAC(AAS).
∴AD=AE;
(2)解:连接OF,如图,
∵F为半圆的中点,
∴∠AOF=∠BOF=90°,
∴OF⊥AB.
∵OA=OF,
∴∠OAF=∠OFA=45°.
∴∠DAE=135°.
由(1)知:△DAC≌△EAC,
∴∠CAD=∠CAE=67.5°.
∴∠DCA=∠ECA=22.5°.
∵∠ACE+∠FCE=∠ACF=∠AOF=45°,
∴∠ECF=22.5°.
∵CE⊥AB,
∴∠AMC=90°﹣∠ECM=67.5°.
15.证明:(1)∵AD∥BC,DF∥AB,
∴四边形ABCD为平行四边形,
∴∠B=∠D,
∵∠AFC=∠B,∠ACF=∠D,
∴∠AFC=∠ACF,
∴AC=AF.
(2)连接AO,CO,如图,
由(1)得∠AFC=∠ACF,
∵∠AFC==75°,
∴∠AOC=2∠AFC=150°,
∴的长l==.
16.解:(1)①∵∠ABC=30°,
∴∠AED=∠ABD=30°,
由折叠可知:∠ACB=∠AED=30°;
②∵AD=DE.
∴∠DAE=∠DEA,
∴∠DEA=∠DBA=DAE=30°,
由折叠可知:∠DAE=∠DAC=30°,
∵∠ABC=∠ACB=30°,
∴∠CAB=180°﹣∠ABC﹣∠ACB=120°,
∴∠CAE=∠CAD+∠EAD=60°,
∴∠EAB=∠CAB﹣∠CAE=120°﹣60°=60°;
(2)∵,
∴+=+,
∴AE=BD,
由折叠的性质可知:∠AED=∠ACD,AE=AC=4,
∵∠ABD=∠AED,
∴∠ABD=∠ACD,
∴AB=AC,
∴AE=AB=BD=4,
∴BC=CD+DB=2+4=6.
17.(1)证明:如图:连接BD,
∵AB⊥CD于E,BF⊥AC于F,
∴∠CFG=∠GEB,
∵∠CGF=∠BGE,
∴∠C=∠GBE,
∴∠C=∠DBE,
∴∠GBE=∠DBE,
∵AB⊥CD于E,
∴∠GEB=∠DEB,
在△GBE和△DBE中,
,
∴△BGE≌△BDE(ASA),
∴ED=EG.
(2)解:如图:
连接OA,设OA=r,则DG=r+1,
由(1)可知ED=EG,
∴OE=,
∵AB⊥CD于E,AB=8,
∴AE=BE=4,
∴在Rt△OAE中,根据勾股定理得:OE2+AE2=OA2,
即()2+42=r2,
解得:r=,
即⊙O的半径为.
18.解:(1)∵OC⊥AB,
∴AD=BD;
(2)设主桥拱半径为R,由题意可知AB=26,CD=5,
∴BD=AB=13,
OD=OC﹣CD=R﹣5,
∵∠OBD=90°,
∴OD2+BD2=OB2,
∴(R﹣5)2+132=R2,
解得R=19.4≈19,
答:这座石拱桥主桥拱的半径约为19m.
19.解:(1)△BDE为等腰直角三角形.理由如下:
∵AE 平分∠BAC,BE 平分∠ABC,
∴∠BAE=∠CAD=∠CBD,∠ABE=∠EBC.
∵∠BED=∠BAE+∠ABE,∠DBE=∠DBC+∠CBE,
∴∠BED=∠DBE.
∴BD=ED.
∵AB为直径,
∴∠ADB=90°
∴△BDE是等腰直角三角形.
另解:计算∠AEB=135°也可以得证.
(2)解:连接OC、CD、OD,OD交BC于点F.
∵∠DBC=∠CAD=∠BAD=∠BCD.
∴BD=DC.
∵OB=OC.
∴OD垂直平分BC.
∵△BDE是等腰直角三角形,BE=2,
∴BD=2.
∵AB=10,
∴OB=OD=5.
设OF=t,则DF=5﹣t.
在Rt△BOF和Rt△BDF中,52﹣t2=(2)2﹣(5﹣t)2,
解得t=3,
∴BF=4.
∴BC=8.
另解:分别延长AC,BD相交于点G.则△MBG为等腰三角形,先计算AG=10,BG=4,AD=4,再根据面积相等求得BC.
20.(1)证明:∵AC是⊙O的直径,
∴∠B=90°,
∵OD⊥AB,
∴∠ODB=90°,
∵PF与⊙O相切于点P,
∴∠OPF=90°,
∴四边形DBFP是矩形;
(2)PE⊥AC,
证明:连接AP,PC,
∵四边形DBFP是矩形,
∴∠PFC=90°,PF∥BD,PF=DB,PD∥BF,
∴∠OPC=∠PCF,∠PDF=∠DFB,
∵OD⊥AB,
∴AD=DB,
∴AD=PF,
∴四边形ADFP是平行四边形,
∴AP∥DF,
∴∠PAE=∠FEC,∠APD=∠PDF,
∴∠APD=∠DFB,
∵OA=OP,
∴∠PAE=∠APD,
∴∠DFB=∠FEC,
∴CE=CF,
∵OP=OC,
∴∠OPC=∠OCP,
∴∠OCP=∠PCF,
∵CP=CP,
∴△CEP≌△CFP(SAS),
∴∠PEC=∠PFC=90°,
∴PE⊥AC.
1.如图,AB是⊙O的直径,点C在⊙O上,=,点D是的中点,连结OC,AD,交于点E,连结BE,BD.
(1)求∠EBA的度数.
(2)求证:AE=BD.
(3)若DE=1,求⊙O的面积.
2.如图,在⊙O中,AC为⊙O的直径,AB为⊙O的弦,点E是的中点,过点E作AB的垂线,交AB于点M,交⊙O于点N,分别连接EB,CN.
(1)EM与BE的数量关系是 ;
(2)求证:=;
(3)若AM=,MB=2,求阴影部分图形的面积.
3.如图,Rt△ABC中,∠C=90°,点O在AC上,以OA为半径的半圆O分别交AB,AC于点D,E,过点D作半圆O的切线DF,交BC于点F.
(1)求证:BF=DF;
(2)若AO=CE=4,CF=1,求BF的长.
4.如图,在△ABC中,以AB为直径的⊙O交AC于点D,过点D作⊙O的切线,交BC于点E,连接BD.
(1)判断∠ABD与∠CDE的数量关系,并说明理由.
(2)若∠EDB=40°,OB=4,求的长.
5.如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,OE⊥AB于点H,连接CE,过点C作⊙O的切线交AB的延长线于点D.
(1)求证:∠COE=2∠DCE;
(2)若AB=8,EH=2,求BD的长.
6.如图,△ABC内接于⊙O,∠ACB=45°,AD是⊙O的直径,过点B作AD的平行线,交AC的延长线于点P.
(1)求证:PB是⊙O的切线;
(2)若AB=2,∠CAB=30°,则的长为 .(结果保留π)
7.如图,在⊙O中,直径AB垂直于弦CD,垂足为E,连接AC,将△ACE沿AC翻折得到△ACF,直线FC与直线AB相交于点G.
(1)直线FC与⊙O有何位置关系?并说明理由;
(2)若OB=GB=2,求GF的长.
8.如图,AB为⊙O的直径,CD是⊙O的弦,延长DC交切线AF于点F,交AB于点E,若AC=CE.
(1)求证:AF=AD;
(2)若EF=5,AD=4,求点O到AD的距离.
9.如图,四边形ABCD内接于⊙O,BD为⊙O的直径,AC平分∠BAD,CD=2,点E在BC的延长线上,连接DE.
(1)求直径BD的长;
(2)若BE=5,计算图中阴影部分的面积.
10.如图,四边形ABCD是⊙O的内接四边形,且对角线BD为直径,过点A作⊙O的切线AE,与CD的延长线交于点E,已知DA平分∠BDE.
(1)求证:AE⊥DE;
(2)若⊙O的半径为5,CD=6,求AD的长.
11.如图,AB是⊙O的直径,CD是⊙O的一条弦,AB⊥CD,连接AC,OD.
(1)求证:∠BOD=2∠A;
(2)连接DB,过点C作CE⊥DB,交DB的延长线于点E,延长DO,交AC于点F.若F为AC的中点,求证:直线CE为⊙O的切线.
12.如图,AB是⊙O的切线,B为切点,直线AO交⊙O于C,D两点,连接BC,BD.过圆心O作BC的平行线,分别交AB的延长线、⊙O及BD于点E,F,G.
(1)求证:∠D=∠E;
(2)若F是OE的中点,⊙O的半径为3,求阴影部分的面积.
13.请阅读下列材料,并完成相应的任务:
阿基米德折弦定理,阿基米德(公元前287年一公元前212年),伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家,静态力学和流体静力学的奠基人,并且享有“力学之父”的美称,阿基米德和高斯,牛顿并列为世界三大数学家.
阿拉伯Al﹣Binmi(973年一1050年)的译文中保存了阿基米德折弦定理的内容,苏联在1964年根据Al﹣Binmi译本出版了俄文版《阿基米德全集》,第一题就是阿基米德折弦定理.
阿基米德折弦定理:如图1,AB和BC是⊙O的两条弦(即折线ABC是圆的一条折弦),BC>AB,M是的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=AB+BD.
小明同学运用“截长法”和三角形全等来证明CD=AB+BD,过程如下:
证明:如图2所示,在CB上截取CG=AB,连接MA,MB,MC和MG.
∵M是的中点,∴MA=MC,…
任务:
(1)请按照上述思路,写出该证明的剩余部分;
(2)如图3,已知等边△ABC内接于⊙O,AB=4,D为上一点,∠ABD=45°,AE⊥BD于点E,请直接写出△BDC的周长.
14.如图1,AB是⊙O的直径,点F是⊙O上的一点,连接AF,过点O作OC∥AF交⊙O于点C,过点C作⊙O的切线,交FA的延长线于点D,CE⊥AB于E,连接AC.
(1)求证:AD=AE;
(2)如图2,在图1的条件下,若点F为半圆的中点,连接CF交AB于点M,求∠AMC的度数.
15.如图,△ABC内接于⊙O,AD∥BC交⊙O于点D,DF∥AB交BC于点E,交⊙O于点F,连接AF,CF.
(1)求证:AC=AF;
(2)若⊙O的半径为3,∠CAF=30°,求的长(结果保留π).
16.如图,D是△ABC的BC边上一点,连结AD,作△ABD的外接圆O,将△ADC沿直线AD折叠,点C的对应点E落在⊙O上.
(1)若∠ABC=30°,如图1.
①求∠ACB的度数.
②若AD=DE,求∠EAB的度数.
(2)若,如图2.求BC的长.
17.如图,在⊙O中,AB,AC为弦,CD为直径,AB⊥CD于E,BF⊥AC于F,BF与CD相交于G.
(1)求证:ED=EG;
(2)若AB=8,OG=1,求⊙O的半径.
18.石拱桥是我国古代人民勤劳和智慧的结晶(如图1),隋代建造的赵州桥距今约有1400年历史,是我国古代石拱桥的代表.如图2是根据某石拱桥的实物图画出的几何图形,桥的主桥拱是圆弧形,表示为.桥的跨度(弧所对的弦长)AB=26m,设所在圆的圆心为O,半径OC⊥AB,垂足为D.拱高(弧的中点到弦的距离)CD=5m.连接OB.
(1)直接判断AD与BD的数量关系;
(2)求这座石拱桥主桥拱的半径(精确到1m).
19.如图,以AB为直径的⊙O经过△ABC的顶点C,AE,BE分别平分∠BAC和∠ABC,AE的延长线交⊙O于点D,连接BD.
(1)判断△BDE的形状,并证明你的结论;
(2)若AB=10,BE=2,求BC的长.
20.如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作⊙O的切线与BC的延长线交于F.
(1)如图1,求证:四边形DBFP为矩形;
(2)如图2,连接DF交AC于E,连接PE,判断PE与AC的位置关系,并证明你的结论.
参考答案
1.解:(1)连接AC,
∵=,
∴∠AOC=∠BOC=90°
∴∠CAB=45°,
∵点D是的中点,
∴,
∴∠CAD=∠EAB=22.5°;
(2)由(1)知,OC垂直平分AB,
∴AE=BE,
∴∠DEB=2∠EAB=45°,
∵AB是直径,
∴∠D=90°,
∴BD=sin45°BE,
∴BE=BD,
∴AE=BD;
(3)∵DE=1
∴BD=DE=1,
∴AE=BE=,
∴AD=+1,
在Rt△ABD中,AD2+BD2=(2OA)2,
∴()2+1=4OA2,
∴OA2=,
∴圆的面积为πOA2=.
2.(1)解:结论:BE=EM.
理由:∵AC为⊙O的直径,点E是的中点,
∴∠ABE=45°,
∵AB⊥EN,
∴△BME是等腰直角三角形,
∴BE=EM,
故答案为:BE=EM;
(2)证明:连接EO,
∵AC是⊙O的直径,E是的中点,
∴∠AOE=90°,
∴∠ABE=∠AOE=45°,
∵EN⊥AB,垂足为点M,
∴∠EMB=90°
∴∠ABE=∠BEN=45°,
∴=,
∵点E是的中点,
∴=,
∴=,
∴﹣=﹣,
∴=;
(3)解:连接AE,OB,ON,
∵EN⊥AB,垂足为点M,
∴∠AME=∠EMB=90°,
∵BM=1,由(2)得∠ABE=∠BEN=45°,
∴EM=BM=2,
又∵BE=EM,
∴BE=2,
∵在Rt△AEM中,EM=2,AM=2,
∴∠EAB=30°,
∵∠EAB=∠EOB,
∴∠EOB=60°,
又∵OE=OB,
∴△EOB是等边三角形,
∴OE=BE=2,
又∵=,
∴BE=CN,
∴△OEB≌△OCN(SSS),
∴CN=BE=2
又∵S扇形OCN==π,S△OCN= CN×CN=×2××2=2,
∴S阴影=S扇形OCN﹣S△OCN=π﹣2.
3.(1)证明:连接OD,
∵∠C=90°,
∴∠A+∠B=90°,
∵DF与半⊙O相切于点D,
∴∠ODF=90°,
∴∠ADO+∠BDF=180°﹣∠ODF=90°,
∵OA=OD,
∴∠A=∠ADO,
∴∠B=∠BDF,
∴BF=DF;
(2)解:连接OF,
∵∠C=90°,OC=OE+CE=8,CF=1,
∴OF2=OC2+CF2=82+12=65,
在Rt△ODF中,OD=AO=4,
∴DF====7,
∴DF=BF=7,
∴BF的长为7.
4.解:(1)∠ABD=∠CDE.
证明:连接OD,如图,
∵DE为切线,
∴OD⊥DE,
∴∠ODB+∠BDE=90°,
∵AB为直径,
∴∠ADB=90°,
∴∠CDE+∠BDE=90°,
∴∠ODB=∠CDE,
∵OB=OD,
∴∠ABD=∠ODB,
∴∠ABD=∠CDE;
(2)∵∠EDB=40°,∠ODE=90°,
∴∠ODB=90°﹣∠EDB=90°﹣40°=50°,
∵OD=OB,
∴∠ODB=∠OBD,
∴∠BOD=80°,
∵OB=4,
∴的长==.
5.(1)证明:连接AE,如图,
∵CD为⊙O的切线,
∴AC⊥CD,
∴∠ACD=90°,
即∠ACE+∠DCE=90°,
∵AC是⊙O的直径,
∴∠AEC=90°,
∴∠ACE+∠CAE=90°,
∴∠CAE=∠DCE,
∵∠COE=2∠CAE,
∴∠COE=2∠DCE;
(2)解:∵OE⊥AB,
∴AH=BH=AB=4,
设⊙O的半径为r,则OH=r﹣2,OA=r,
在Rt△AOH中,42+(r﹣2)2=r2,
解得r=5,
∴AC=2r=10,
∵∠CAB=∠DAC,∠ABC=∠ACD,
∴AC:AB=AD:AC,即10:8=AD:10,
解得AD=,
∴BD=AD﹣AB=﹣8=.
6.(1)证明:连接OB,
∵∠ACB=45°,
∴∠AOB=2∠ACB=90°,
∵AD∥BP,
∴∠AOB=∠OBP=90°,
∵OB是⊙O的半径,
∴PB是⊙O的切线;
(2)解:连接OC,
∵∠AOB=90°,OA=BO,AB=2,
∴OA=OB==,
∵∠CAB=30°,
∴∠COB=2∠CAB=60°,
∴的长==,
故答案为:.
7.解:(1)FG是⊙O的切线;
理由:连接OC,如图,
∵OA=OC,
∴∠OAC=∠OCA,
∵△ACE沿AC翻折得到△ACF,
∴∠OAC=∠FAC,∠F=∠AEC=90°,
∴∠OCA=∠FAC,
∴OC∥AF,
∴∠OCG=∠F=90°,
∴OC⊥FG,
∵OC是⊙O的半径,
∴直线FC与⊙O相切;
(2)∵OB=GB=OC=2,∠OCG=90°,
∴OC=OG,
∴∠G=30°,AG=6,
∵∠F=90°,
∴FG=AG=3.
8.(1)证明:连接BC,
∵CA=CE,
∴∠CAE=∠CEA,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAE+∠B=90°,
∵AF与⊙O相切于点A,
∴∠BAF=90°,
∴∠AEC+∠F=90°,
∴∠F=∠B,
∵∠B=∠D,
∴∠D=∠F,
∴AF=AD;
(2)解:连接BD,过点O作OH⊥AB,垂足为H,
∴AH=DH,
∵OA=OB,
∴OH是△ABD的中位线,
∴OH=BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
在Rt△AFE中,FE=5,AF=AD=4,
∴AE===3,
∵∠F+∠AEF=90°,∠FAC+∠CAE=90°,∠AEF=∠CAE,
∴∠F=∠FAC,
∴CF=AC,
∵AC=CE,
∴AC=CF=CE=EF=2.5,
∵∠CAE=∠CDB,∠CEA=∠BED,
∴∠BED=∠CDB,
∴BE=BD,
设BE=BD=x,
∴AB=AE+BE=3+x,
在Rt△ABD中,AD2+BD2=AB2,
∴16+x2=(3+x)2,
∴x=,
∴BD=,
∴OH=BD=,
∴点O到AD的距离为.
9.解:(1)∵BD为⊙O的直径,
∴∠BCD=∠DCE=90°,
∵AC平分∠BAD,
∴∠BAC=∠DAC,
∴BC=DC=2,
∴BD=2×=4;
(2)∵BE=5,
∴CE=3,
∵BC=DC,
∴S阴影=S△CDE=×2×=6.
10.(1)证明:连接OA,
∵AE是⊙O的切线,
∴∠OAE=90°,
∵OA=OD,
∴∠OAD=∠ODA,
∵DA平分∠BDE,
∴∠ODA=∠ADE,
∴∠ADE=∠OAD,
∴OA∥CE,
∴∠E=180°﹣∠OAE=90°,
∴AE⊥DE;
(2)解:过点O作OF⊥DC,垂足为F,
∴∠OFD=90°,
∵∠OAE=∠E=90°,
∴四边形OAEF是矩形,
∴OA=EF=5,AE=OF,
∵OF⊥CD,
∴DF=CD=3,
∴DE=EF﹣DF=5﹣3=2,
∴OF===4,
∵AE=OF=4,
∴AD===2,
∴AD的长为2.
11.证明:(1)如图,连接AD,
∵AB是⊙O的直径,AB⊥CD,
∴,
∴∠CAB=∠BAD,
∵∠BOD=2∠BAD,
∴∠BOD=2∠A;
(2)如图,连接OC,
∵F为AC的中点,
∴DF⊥AC,
∴AD=CD,
∴∠ADF=∠CDF,
∵,
∴∠CAB=∠DAB,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠CDF=∠CAB,
∵OC=OD,
∴∠CDF=∠OCD,
∴∠OCD=∠CAB,
∵,
∴∠CAB=∠CDE,
∴∠CDE=∠OCD,
∵∠E=90°,
∴∠CDE+∠DCE=90°,
∴∠OCD+∠DCE=90°,
即OC⊥CE,
∵OC为半径,
∴直线CE为⊙O的切线.
12.(1)证明:连接OB,
∵AB是⊙O的切线,
∴∠OBE=90°,
∴∠E+∠BOE=90°,
∵CD为⊙O的直径,
∴∠CBD=90°,
∴∠D+∠DCB=90°,
∵OE∥BC,
∴∠BOE=∠OBC,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠BOE=∠OCB,
∴∠D=∠E;
(2)解:∵F为OE的中点,OB=OF,
∴OF=EF=3,
∴OE=6,
∴BO=OE,
∵∠OBE=90°,
∴∠E=30°,
∴∠BOG=60°,
∵OE∥BC,∠DBC=90°,
∴∠OGB=90°,
∴OG=,BG=,
∴S△BOG=OG BG==,S扇形BOF==π,
∴S阴影部分=S扇形BOF﹣S△BOG=.
13.解:(1)∵
∴∠A=∠C,
∵M是的中点,
∴MA=MC,
在△MBA≌△MCG中,
,
∴△MBA≌△MCG(SAS),
∴MB=MG,
∵MD⊥BC,
∴BD=GD,
∴CG+GD=AB+BD,
即CD=AB+BD;
(2)∵△ABC是等边三角形,
∴AB=AC,
∴,
由阿基米德折弦定理,可得BE=ED+DC,
∵∠ABD=45°,AB=4,∠AEB=90°,
∴BE=AB=2,
故△BDC的周长为:BC+BD+CD=BC+BE+ED+DC=BC+2BE=4+4.
14.(1)证明:∵CD是⊙O的切线,
∴OC⊥CD,
∴∠DCA+∠OCA=90°.
∵OC=OA,
∴∠OCA=∠OAC.
∴∠OAC+∠DCA=90°.
∵CE⊥AB,
∴∠OAC+∠ECA=90°.
∴∠DCA=∠ECA.
∵OC∥AF,OC⊥CD,
∴CD⊥AF,
∴∠D=90°.
在△DAC和△EAC中,
,
∴△DAC≌△EAC(AAS).
∴AD=AE;
(2)解:连接OF,如图,
∵F为半圆的中点,
∴∠AOF=∠BOF=90°,
∴OF⊥AB.
∵OA=OF,
∴∠OAF=∠OFA=45°.
∴∠DAE=135°.
由(1)知:△DAC≌△EAC,
∴∠CAD=∠CAE=67.5°.
∴∠DCA=∠ECA=22.5°.
∵∠ACE+∠FCE=∠ACF=∠AOF=45°,
∴∠ECF=22.5°.
∵CE⊥AB,
∴∠AMC=90°﹣∠ECM=67.5°.
15.证明:(1)∵AD∥BC,DF∥AB,
∴四边形ABCD为平行四边形,
∴∠B=∠D,
∵∠AFC=∠B,∠ACF=∠D,
∴∠AFC=∠ACF,
∴AC=AF.
(2)连接AO,CO,如图,
由(1)得∠AFC=∠ACF,
∵∠AFC==75°,
∴∠AOC=2∠AFC=150°,
∴的长l==.
16.解:(1)①∵∠ABC=30°,
∴∠AED=∠ABD=30°,
由折叠可知:∠ACB=∠AED=30°;
②∵AD=DE.
∴∠DAE=∠DEA,
∴∠DEA=∠DBA=DAE=30°,
由折叠可知:∠DAE=∠DAC=30°,
∵∠ABC=∠ACB=30°,
∴∠CAB=180°﹣∠ABC﹣∠ACB=120°,
∴∠CAE=∠CAD+∠EAD=60°,
∴∠EAB=∠CAB﹣∠CAE=120°﹣60°=60°;
(2)∵,
∴+=+,
∴AE=BD,
由折叠的性质可知:∠AED=∠ACD,AE=AC=4,
∵∠ABD=∠AED,
∴∠ABD=∠ACD,
∴AB=AC,
∴AE=AB=BD=4,
∴BC=CD+DB=2+4=6.
17.(1)证明:如图:连接BD,
∵AB⊥CD于E,BF⊥AC于F,
∴∠CFG=∠GEB,
∵∠CGF=∠BGE,
∴∠C=∠GBE,
∴∠C=∠DBE,
∴∠GBE=∠DBE,
∵AB⊥CD于E,
∴∠GEB=∠DEB,
在△GBE和△DBE中,
,
∴△BGE≌△BDE(ASA),
∴ED=EG.
(2)解:如图:
连接OA,设OA=r,则DG=r+1,
由(1)可知ED=EG,
∴OE=,
∵AB⊥CD于E,AB=8,
∴AE=BE=4,
∴在Rt△OAE中,根据勾股定理得:OE2+AE2=OA2,
即()2+42=r2,
解得:r=,
即⊙O的半径为.
18.解:(1)∵OC⊥AB,
∴AD=BD;
(2)设主桥拱半径为R,由题意可知AB=26,CD=5,
∴BD=AB=13,
OD=OC﹣CD=R﹣5,
∵∠OBD=90°,
∴OD2+BD2=OB2,
∴(R﹣5)2+132=R2,
解得R=19.4≈19,
答:这座石拱桥主桥拱的半径约为19m.
19.解:(1)△BDE为等腰直角三角形.理由如下:
∵AE 平分∠BAC,BE 平分∠ABC,
∴∠BAE=∠CAD=∠CBD,∠ABE=∠EBC.
∵∠BED=∠BAE+∠ABE,∠DBE=∠DBC+∠CBE,
∴∠BED=∠DBE.
∴BD=ED.
∵AB为直径,
∴∠ADB=90°
∴△BDE是等腰直角三角形.
另解:计算∠AEB=135°也可以得证.
(2)解:连接OC、CD、OD,OD交BC于点F.
∵∠DBC=∠CAD=∠BAD=∠BCD.
∴BD=DC.
∵OB=OC.
∴OD垂直平分BC.
∵△BDE是等腰直角三角形,BE=2,
∴BD=2.
∵AB=10,
∴OB=OD=5.
设OF=t,则DF=5﹣t.
在Rt△BOF和Rt△BDF中,52﹣t2=(2)2﹣(5﹣t)2,
解得t=3,
∴BF=4.
∴BC=8.
另解:分别延长AC,BD相交于点G.则△MBG为等腰三角形,先计算AG=10,BG=4,AD=4,再根据面积相等求得BC.
20.(1)证明:∵AC是⊙O的直径,
∴∠B=90°,
∵OD⊥AB,
∴∠ODB=90°,
∵PF与⊙O相切于点P,
∴∠OPF=90°,
∴四边形DBFP是矩形;
(2)PE⊥AC,
证明:连接AP,PC,
∵四边形DBFP是矩形,
∴∠PFC=90°,PF∥BD,PF=DB,PD∥BF,
∴∠OPC=∠PCF,∠PDF=∠DFB,
∵OD⊥AB,
∴AD=DB,
∴AD=PF,
∴四边形ADFP是平行四边形,
∴AP∥DF,
∴∠PAE=∠FEC,∠APD=∠PDF,
∴∠APD=∠DFB,
∵OA=OP,
∴∠PAE=∠APD,
∴∠DFB=∠FEC,
∴CE=CF,
∵OP=OC,
∴∠OPC=∠OCP,
∴∠OCP=∠PCF,
∵CP=CP,
∴△CEP≌△CFP(SAS),
∴∠PEC=∠PFC=90°,
∴PE⊥AC.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
