2022-2023学年苏科版九年级数学上册2.7弧长及扇形的面积 同步达标测试题(word、含解析)
文档属性
| 名称 | 2022-2023学年苏科版九年级数学上册2.7弧长及扇形的面积 同步达标测试题(word、含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 466.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-17 00:00:00 | ||
图片预览



文档简介
2022-2023学年苏科版九年级数学上册《2.7弧长及扇形面积》同步达标测试题(附答案)
一.选择题(共7小题,满分28分)
1.如图,点A、B、C是半径为8的⊙O上的三点.如果∠ACB=45°,那么的长为( )
A.90° B.2π C.3π D.4π
2.已知水平放置半径为6cm的球形容器中装有溶液,容器内液面的面积为27πcm2.如图,是该球体的一个最大纵截面,则该截面⊙O中阴影部分的弧长为( )
A.2πcm B.4πcm C.6πcm D.8πcm
3.如图,在平行四边形ABCD中,AD=6,以AD为直径的⊙O恰好经过点B,交BC于点E,当点E为的中点时,下列结论错误的是( )
A.AE平分∠BAD B.
C. D.的长为2π
4.如图,在正方形ABCD中,以点A为圆心,AB长为半径作弧MN.若∠1=∠2,AB=2,则弧MN的长为( )
A.π B. C.π D.2π
5.如图,在扇形BOC中,∠BOC=60°,OD平分∠BOC交BC于点D,点E为半径OB上一动点.若OB=2,则阴影部分周长的最小值为( )
A. B. C. D.
6.如图,边长为2的正方形ABCD的中心与半径为2的⊙O的圆心重合,E,F分别是AD,BA的延长线与⊙O的交点,则图中阴影部分的面积为( )
A.2π﹣2 B.2π﹣2 C.2π+2 D.2π+2
7.边长为2的两种正方形卡片如下图①所示,卡片中的扇形半径均为2.图②是交替摆放A、B两种卡片得到的图案.若摆放这个图案共用两种卡片2021张,则这个图案中阴影部分图形的面积和为( )
A.4040 B.4044–π C.4044 D.4044+π
二.填空题(共7小题,满分28分)
8.已知圆的半径为3,扇形的圆心角为120°,则扇形的弧长为 .
9.若扇形的圆心角为120°,半径为,则它的弧长为 .
10.如图是古希腊数学家埃拉托斯特尼在夏至这天测量地球子午线周长的示意图,其中,太阳光线AB∥CD,CE是竖直插在球面上的木杆,AB、CE的延长线都经过圆心O.已知B、E间的劣弧长约为800千米,子午线周长约为40000千米,则∠DCE的度数为 .
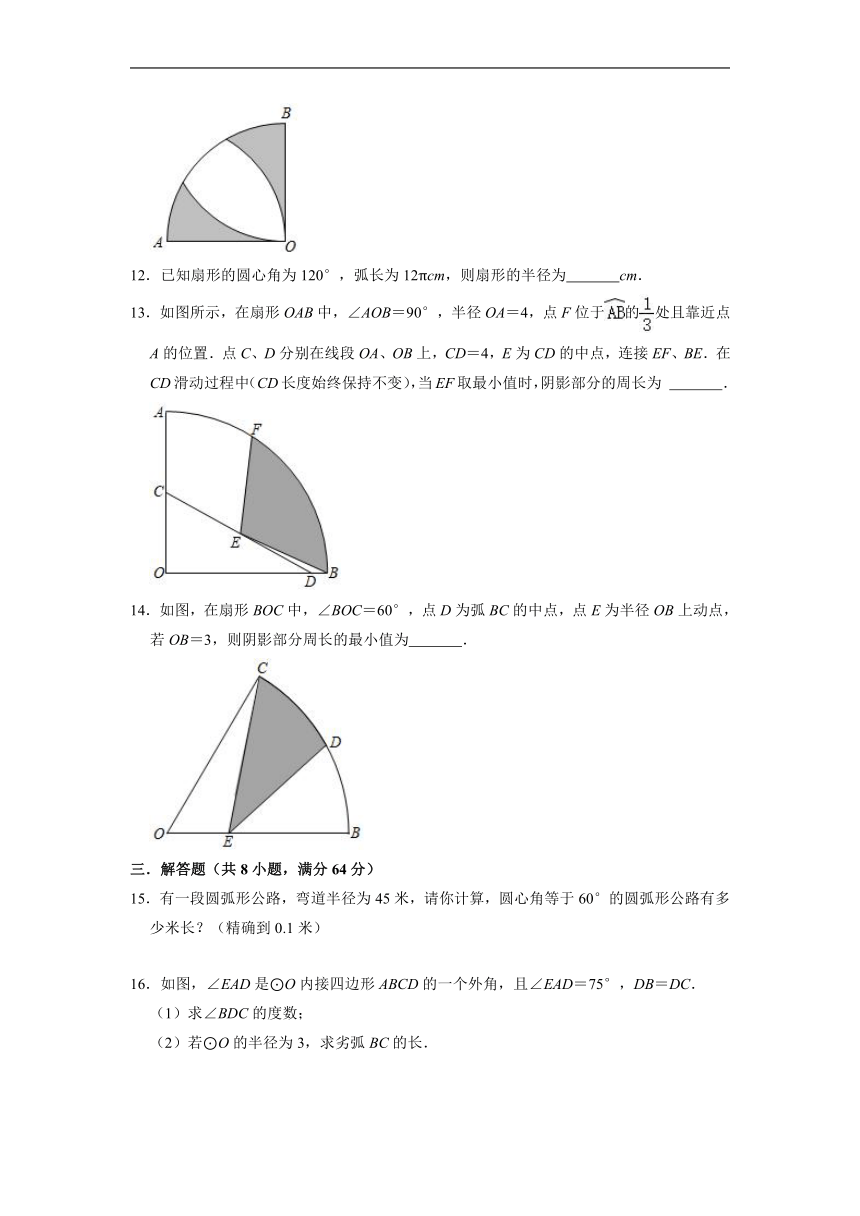
11.如图,在扇形AOB中,∠AOB=90°,AO=6,分别以点A,B为圆心,AO,BO的长为半径画弧,与相交,则图中阴影部分的周长为 .
12.已知扇形的圆心角为120°,弧长为12πcm,则扇形的半径为 cm.
13.如图所示,在扇形OAB中,∠AOB=90°,半径OA=4,点F位于的处且靠近点A的位置.点C、D分别在线段OA、OB上,CD=4,E为CD的中点,连接EF、BE.在CD滑动过程中(CD长度始终保持不变),当EF取最小值时,阴影部分的周长为 .
14.如图,在扇形BOC中,∠BOC=60°,点D为弧BC的中点,点E为半径OB上动点,若OB=3,则阴影部分周长的最小值为 .
三.解答题(共8小题,满分64分)
15.有一段圆弧形公路,弯道半径为45米,请你计算,圆心角等于60°的圆弧形公路有多少米长?(精确到0.1米)
16.如图,∠EAD是⊙O内接四边形ABCD的一个外角,且∠EAD=75°,DB=DC.
(1)求∠BDC的度数;
(2)若⊙O的半径为3,求劣弧BC的长.
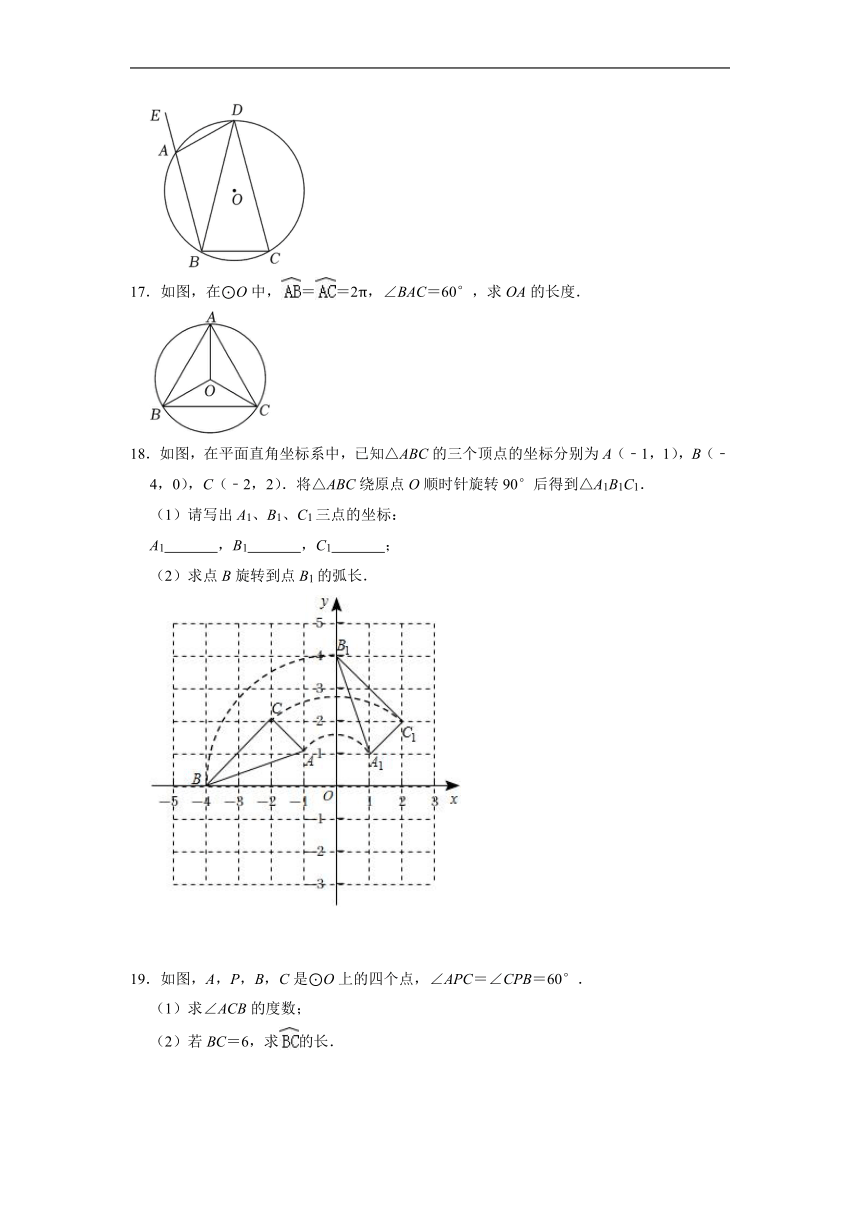
17.如图,在⊙O中,==2π,∠BAC=60°,求OA的长度.
18.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣1,1),B(﹣4,0),C(﹣2,2).将△ABC绕原点O顺时针旋转90°后得到△A1B1C1.
(1)请写出A1、B1、C1三点的坐标:
A1 ,B1 ,C1 ;
(2)求点B旋转到点B1的弧长.
19.如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求∠ACB的度数;
(2)若BC=6,求的长.
20.如图1,在⊙O中,AC=BD,且AC⊥BD,垂足为点E.
(1)求∠ABD的度数;
(2)图2,连接OA,当OA=2,∠OAB=15°,求BE的长度;
(3)在(2)的条件下,求的长.
21.如图,已知Rt△ABD中,∠A=90°,将斜边BD绕点B顺时针方向旋转至BC,使BC∥AD,过点C作CE⊥BD于点E.
(1)求证:△ABD≌△ECB;
(2)若∠ABD=30°,BE=3,求弧CD的长.
22.如图,已知四边形ABCD内接于圆O,且∠A=105°,BD=CD
(1)求∠DBC的度数
(2)若⊙O的半径为3,求的长.
参考答案
一.选择题(共7小题,满分28分)
1.解:如图,连接OA、OB.
∵∠ACB=45°,
∴∠AOB=90°,
∵OA=8,
∴的长是:=4π.
故选:D.
2.解:连接OA,OB,过点O作OH⊥AB于H则AH=BH.
由题意π AH2=27π,
∴AH2=27,
∵AH>0,
∴AH=3,
∴∠AOH=60°,
∵OA=OB,OH⊥AB,
∴∠AOH=∠BOH=60°,
∴∠AOB=120°,
∴的长==4π(cm).
故选:B.
3.解:A.∵点E为的中点,
∴,
∴∠BAE=∠EAD,
∴AE平分∠BAD,
故A不符合题意;
B.∵四边形ABCD是平行四边形,
∴BE∥AO,
∴∠BEA=∠EAO,
∵∠BAE=∠EAO,
∴∠BAE=∠BEA,
∴,
∴△AOB和△BOE是等边三角形,
∴OA=BE,
∵BC=AD,
∴EC=OD,
∵EC∥OD,
∴四边形ECDO是平行四边形,
∵△AOB和△BOE是等边三角形,
∴∠EOD=60°,
∵OE=3,
∴EH=,
∴S阴影=OD×EH﹣=
故B符合题意;
C.由B可知,,
故C不符合题意;
D.的长为:=2π,
故D不符合题意.
故选:B.
4.解:∵四边形ABCD是正方形,
∴∠DAB=90°,
∵∠1=∠2,
∴∠NAM=90°,
∵以点A为圆心,AB长为半径作弧MN,AB=2,
∴AN=2,
∴弧MN的长为:l===π,
故选:C.
5.解:如图,作点D关于OB的对称点D′,连接D′C交OB于点E′,连接E′D、OD′,
此时E′C+E′D最小,即:E′C+E′D=CD′,
由题意得,∠COD=∠DOB=∠BOD′=30°,
∴∠COD′=90°,
∴CD′===2,
的长==,
∴阴影部分周长的最小值为2+=.
故选:C.
6.解:延长DC,CB交⊙O于M,N,连接OF,过点O作OH⊥AB于H.
在Rt△OFH中,FH===,
∵AH=BH=,
∴AF=﹣,
∴S△DAF= AD AF=×2×(﹣)=2﹣2,
则图中阴影部分的面积=×(S圆O﹣S正方形ABCD)﹣S△ADF= [π (2)2﹣2×2]﹣(2﹣2)=2π﹣2,
故选:A.
7.解:2021÷2=1010…1,
所以这个图案中阴影部分图形的面积和为:4×1010+A的阴影面积,
是:4440+4﹣π=4044﹣π.
故选:B.
二.填空题(共7小题,满分28分)
8.解:扇形的弧长==2π,
故答案为:2π.
9.解:∵扇形的圆心角为120°,半径为,
∴它的弧长为:=π,
故答案为:π.
10.解:设⊙O的半径为r千米,∠AOE=x°,
由题意可得:2πr=40000,
∴r=,
∵劣弧BE的弧长为800千米,l=,
∴=800,
解得x=7.2,
即∠AOE=7.2°,
∵AB∥CD,
∴∠DCE=∠AOE=7.2°.
故答案为:7.2°.
11.解:如图,连接AC、OC,则AC=AO=OC,
所以△AOC是正三角形,
由题意可知,弧BC,弧AD所对应的圆心角度数为30°且半径为6,弧OD、弧OC所对应的圆心角度数为60°且半径为6,
所以阴影部分的周长为:圆心角为180°半径为6的半圆弧长加直径长,
即:6π+12,
故答案为:6π+12.
12.解:设扇形的半径为rcm,
∵扇形的圆心角为120°,弧长为12πcm,
∴=12π,
解得:r=18,
即扇形的半径是18cm,
故答案为:18.
13.解:如图,连接OF,OE,BF,取OF的中点T,连接BT.
∵∠AOB=90°,=,
∴∠BOF=60°,
∴的长==π,
∵CE=DE,
∴OE=CD=2,
∵OF=4,
∴EF≥OF﹣OE=2,
∴当O,E,F共线时,EF的值最小,此时点E与点T重合,
∴此时EF=2,
∵OF=OB,∠BOF=60°,
∴△BOF是等边三角形,
∵OT=TF,
∴BT⊥OF,
∴BE=BT===2,
∴此时阴影部分的周长为2+2+π.
故答案为:2+2+π.
14.解:如图,作点D关于OB的对称点D′,连接D′C交OB于点E′,连接E′D、OD′,
此时E′C+E′D最小,即:E′C+E′D=CD′,
由题意得,∠COD=∠DOB=∠BOD′=30°,
∴∠COD′=90°,
∴CD′===3,
∴的长l==,
∴阴影部分周长的最小值为3+.
故答案为:3+.
三.解答题(共8小题,满分64分)
15.解:圆心角等于60°的圆弧形公路长为=15π≈47.1米,
答:圆心角等于60°的圆弧形公路长47.1米.
16.解:(1)∵四边形ABCD是⊙O的内接四边形,
∴∠DAB+∠C=180°,
∵∠EAD+∠DAB=180°,
∴∠C=∠EAD,
∵∠EAD=75°,
∴∠C=75°,
∵DB=DC,
∴∠DBC=∠C=75°,
∴∠BDC=180°﹣∠C﹣∠DBC=30°;
(2)连接OB、OC,
∵∠BDC=30°,
∴∠BOC=2∠BDC=60°(圆周角定理),
∵⊙O的半径为3
∴的长是=π.
17.解:∵∠BAC=60°,
∴∠BOC=120°,
∵==2π,
∴∠AOB=∠AOC==120°,
∴=2π,
∴OA=3.
故OA的长度为3.
18.解:(1)由图知,A1(1,1),B1(0,4),C1(2,2),
故答案为:(1,1),(0,4),(2,2);
(2)由题意知,点B旋转到点B1的弧所在的圆的半径为4,弧所对的圆心角为90°,
∴弧长为:=2π.
19.解:(1)∵∠APC=∠CPB=60°,
∴由圆周角定理得:∠ABC=∠APC=60°,∠BAC=∠BPC=60°,
∴∠ACB=180°﹣∠ABC﹣∠BAC=60°;
(2)连结OB,OC,过点O作OD⊥BC于点D,
∵∠BAC=60°,
∴∠BOC=2∠BAC=120°.
∵OD⊥BC于点D,OB=OC,
∴∠BOD=BOC=60°,
BD=BC==3,
∵Rt△BOD中,,
∴,
∴的长=.
20.解:(1)如图1,过点O作OM⊥AC,ON⊥BD,垂足分别为M、N,
∵AC⊥BD,
∴∠MEN=90°=∠ONE=∠OME,
∴四边形OMEN是矩形,
又∵AC=BD,OM⊥AC,ON⊥BD,
∴OM=ON,AM=CM=BN=DN,
∴四边形OMEN是正方形,
∴ME=NE,
∴ME+AM=NE+BN,
即AE=BE,
∴△ABE是等腰直角三角形,
∴∠ABD=45°;
(2)如图2,由(1)可得AM=BN,OM=NE,∠ABD=∠BAC=45°,
∵∠OAB=15°,
∴∠OAM=45°﹣15°=30°,
在Rt△AOM中,∠OAM=30°,OA=2,
∴OM=OA=1,AM=OA=,
∴BE=BN+NE=+1;
(3)如图2,连接OB、OC、OD,
∵OA=OB,∠OAB=15°,
∴∠AOB=180°﹣15°﹣15°=150°,
∵∠ABD=∠BAC=45°,
∴∠AOD=∠BOC=45°×2=90°,
∴∠COD=360°﹣150°﹣90°﹣90°=30°,
∴==.
21.(1)证明:∵∠A=90°,CE⊥BD,
∴∠A=∠BEC=90°.
∵BC∥AD,
∴∠ADB=∠EBC.
∵将斜边BD绕点B顺时针方向旋转至BC,
∴BD=BC.
在△ABD和△ECB中,
∴△ABD≌△ECB;
(2)∵△ABD≌△ECB,
∴AD=BE=3.
∵∠A=90°,∠BAD=30°,
∴BD=2AD=6,
∵BC∥AD,
∴∠A+∠ABC=180°,
∴∠ABC=90°,
∴∠DBC=60°,
∴弧CD的长为=2π.
22.解:(1)∵四边形ABCD内接于圆O,
∴∠DCB+∠BAD=180°,
∵∠A=105°,
∴∠C=180°﹣105°=75°,
∵BD=CD,
∴∠DBC=∠C=75°;
(2)连接BO、CO,
∵∠C=∠DBC=75°,
∴∠BDC=30°,
∴∠BOC=60°,
故的长l==π.
一.选择题(共7小题,满分28分)
1.如图,点A、B、C是半径为8的⊙O上的三点.如果∠ACB=45°,那么的长为( )
A.90° B.2π C.3π D.4π
2.已知水平放置半径为6cm的球形容器中装有溶液,容器内液面的面积为27πcm2.如图,是该球体的一个最大纵截面,则该截面⊙O中阴影部分的弧长为( )
A.2πcm B.4πcm C.6πcm D.8πcm
3.如图,在平行四边形ABCD中,AD=6,以AD为直径的⊙O恰好经过点B,交BC于点E,当点E为的中点时,下列结论错误的是( )
A.AE平分∠BAD B.
C. D.的长为2π
4.如图,在正方形ABCD中,以点A为圆心,AB长为半径作弧MN.若∠1=∠2,AB=2,则弧MN的长为( )
A.π B. C.π D.2π
5.如图,在扇形BOC中,∠BOC=60°,OD平分∠BOC交BC于点D,点E为半径OB上一动点.若OB=2,则阴影部分周长的最小值为( )
A. B. C. D.
6.如图,边长为2的正方形ABCD的中心与半径为2的⊙O的圆心重合,E,F分别是AD,BA的延长线与⊙O的交点,则图中阴影部分的面积为( )
A.2π﹣2 B.2π﹣2 C.2π+2 D.2π+2
7.边长为2的两种正方形卡片如下图①所示,卡片中的扇形半径均为2.图②是交替摆放A、B两种卡片得到的图案.若摆放这个图案共用两种卡片2021张,则这个图案中阴影部分图形的面积和为( )
A.4040 B.4044–π C.4044 D.4044+π
二.填空题(共7小题,满分28分)
8.已知圆的半径为3,扇形的圆心角为120°,则扇形的弧长为 .
9.若扇形的圆心角为120°,半径为,则它的弧长为 .
10.如图是古希腊数学家埃拉托斯特尼在夏至这天测量地球子午线周长的示意图,其中,太阳光线AB∥CD,CE是竖直插在球面上的木杆,AB、CE的延长线都经过圆心O.已知B、E间的劣弧长约为800千米,子午线周长约为40000千米,则∠DCE的度数为 .
11.如图,在扇形AOB中,∠AOB=90°,AO=6,分别以点A,B为圆心,AO,BO的长为半径画弧,与相交,则图中阴影部分的周长为 .
12.已知扇形的圆心角为120°,弧长为12πcm,则扇形的半径为 cm.
13.如图所示,在扇形OAB中,∠AOB=90°,半径OA=4,点F位于的处且靠近点A的位置.点C、D分别在线段OA、OB上,CD=4,E为CD的中点,连接EF、BE.在CD滑动过程中(CD长度始终保持不变),当EF取最小值时,阴影部分的周长为 .
14.如图,在扇形BOC中,∠BOC=60°,点D为弧BC的中点,点E为半径OB上动点,若OB=3,则阴影部分周长的最小值为 .
三.解答题(共8小题,满分64分)
15.有一段圆弧形公路,弯道半径为45米,请你计算,圆心角等于60°的圆弧形公路有多少米长?(精确到0.1米)
16.如图,∠EAD是⊙O内接四边形ABCD的一个外角,且∠EAD=75°,DB=DC.
(1)求∠BDC的度数;
(2)若⊙O的半径为3,求劣弧BC的长.
17.如图,在⊙O中,==2π,∠BAC=60°,求OA的长度.
18.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣1,1),B(﹣4,0),C(﹣2,2).将△ABC绕原点O顺时针旋转90°后得到△A1B1C1.
(1)请写出A1、B1、C1三点的坐标:
A1 ,B1 ,C1 ;
(2)求点B旋转到点B1的弧长.
19.如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求∠ACB的度数;
(2)若BC=6,求的长.
20.如图1,在⊙O中,AC=BD,且AC⊥BD,垂足为点E.
(1)求∠ABD的度数;
(2)图2,连接OA,当OA=2,∠OAB=15°,求BE的长度;
(3)在(2)的条件下,求的长.
21.如图,已知Rt△ABD中,∠A=90°,将斜边BD绕点B顺时针方向旋转至BC,使BC∥AD,过点C作CE⊥BD于点E.
(1)求证:△ABD≌△ECB;
(2)若∠ABD=30°,BE=3,求弧CD的长.
22.如图,已知四边形ABCD内接于圆O,且∠A=105°,BD=CD
(1)求∠DBC的度数
(2)若⊙O的半径为3,求的长.
参考答案
一.选择题(共7小题,满分28分)
1.解:如图,连接OA、OB.
∵∠ACB=45°,
∴∠AOB=90°,
∵OA=8,
∴的长是:=4π.
故选:D.
2.解:连接OA,OB,过点O作OH⊥AB于H则AH=BH.
由题意π AH2=27π,
∴AH2=27,
∵AH>0,
∴AH=3,
∴∠AOH=60°,
∵OA=OB,OH⊥AB,
∴∠AOH=∠BOH=60°,
∴∠AOB=120°,
∴的长==4π(cm).
故选:B.
3.解:A.∵点E为的中点,
∴,
∴∠BAE=∠EAD,
∴AE平分∠BAD,
故A不符合题意;
B.∵四边形ABCD是平行四边形,
∴BE∥AO,
∴∠BEA=∠EAO,
∵∠BAE=∠EAO,
∴∠BAE=∠BEA,
∴,
∴△AOB和△BOE是等边三角形,
∴OA=BE,
∵BC=AD,
∴EC=OD,
∵EC∥OD,
∴四边形ECDO是平行四边形,
∵△AOB和△BOE是等边三角形,
∴∠EOD=60°,
∵OE=3,
∴EH=,
∴S阴影=OD×EH﹣=
故B符合题意;
C.由B可知,,
故C不符合题意;
D.的长为:=2π,
故D不符合题意.
故选:B.
4.解:∵四边形ABCD是正方形,
∴∠DAB=90°,
∵∠1=∠2,
∴∠NAM=90°,
∵以点A为圆心,AB长为半径作弧MN,AB=2,
∴AN=2,
∴弧MN的长为:l===π,
故选:C.
5.解:如图,作点D关于OB的对称点D′,连接D′C交OB于点E′,连接E′D、OD′,
此时E′C+E′D最小,即:E′C+E′D=CD′,
由题意得,∠COD=∠DOB=∠BOD′=30°,
∴∠COD′=90°,
∴CD′===2,
的长==,
∴阴影部分周长的最小值为2+=.
故选:C.
6.解:延长DC,CB交⊙O于M,N,连接OF,过点O作OH⊥AB于H.
在Rt△OFH中,FH===,
∵AH=BH=,
∴AF=﹣,
∴S△DAF= AD AF=×2×(﹣)=2﹣2,
则图中阴影部分的面积=×(S圆O﹣S正方形ABCD)﹣S△ADF= [π (2)2﹣2×2]﹣(2﹣2)=2π﹣2,
故选:A.
7.解:2021÷2=1010…1,
所以这个图案中阴影部分图形的面积和为:4×1010+A的阴影面积,
是:4440+4﹣π=4044﹣π.
故选:B.
二.填空题(共7小题,满分28分)
8.解:扇形的弧长==2π,
故答案为:2π.
9.解:∵扇形的圆心角为120°,半径为,
∴它的弧长为:=π,
故答案为:π.
10.解:设⊙O的半径为r千米,∠AOE=x°,
由题意可得:2πr=40000,
∴r=,
∵劣弧BE的弧长为800千米,l=,
∴=800,
解得x=7.2,
即∠AOE=7.2°,
∵AB∥CD,
∴∠DCE=∠AOE=7.2°.
故答案为:7.2°.
11.解:如图,连接AC、OC,则AC=AO=OC,
所以△AOC是正三角形,
由题意可知,弧BC,弧AD所对应的圆心角度数为30°且半径为6,弧OD、弧OC所对应的圆心角度数为60°且半径为6,
所以阴影部分的周长为:圆心角为180°半径为6的半圆弧长加直径长,
即:6π+12,
故答案为:6π+12.
12.解:设扇形的半径为rcm,
∵扇形的圆心角为120°,弧长为12πcm,
∴=12π,
解得:r=18,
即扇形的半径是18cm,
故答案为:18.
13.解:如图,连接OF,OE,BF,取OF的中点T,连接BT.
∵∠AOB=90°,=,
∴∠BOF=60°,
∴的长==π,
∵CE=DE,
∴OE=CD=2,
∵OF=4,
∴EF≥OF﹣OE=2,
∴当O,E,F共线时,EF的值最小,此时点E与点T重合,
∴此时EF=2,
∵OF=OB,∠BOF=60°,
∴△BOF是等边三角形,
∵OT=TF,
∴BT⊥OF,
∴BE=BT===2,
∴此时阴影部分的周长为2+2+π.
故答案为:2+2+π.
14.解:如图,作点D关于OB的对称点D′,连接D′C交OB于点E′,连接E′D、OD′,
此时E′C+E′D最小,即:E′C+E′D=CD′,
由题意得,∠COD=∠DOB=∠BOD′=30°,
∴∠COD′=90°,
∴CD′===3,
∴的长l==,
∴阴影部分周长的最小值为3+.
故答案为:3+.
三.解答题(共8小题,满分64分)
15.解:圆心角等于60°的圆弧形公路长为=15π≈47.1米,
答:圆心角等于60°的圆弧形公路长47.1米.
16.解:(1)∵四边形ABCD是⊙O的内接四边形,
∴∠DAB+∠C=180°,
∵∠EAD+∠DAB=180°,
∴∠C=∠EAD,
∵∠EAD=75°,
∴∠C=75°,
∵DB=DC,
∴∠DBC=∠C=75°,
∴∠BDC=180°﹣∠C﹣∠DBC=30°;
(2)连接OB、OC,
∵∠BDC=30°,
∴∠BOC=2∠BDC=60°(圆周角定理),
∵⊙O的半径为3
∴的长是=π.
17.解:∵∠BAC=60°,
∴∠BOC=120°,
∵==2π,
∴∠AOB=∠AOC==120°,
∴=2π,
∴OA=3.
故OA的长度为3.
18.解:(1)由图知,A1(1,1),B1(0,4),C1(2,2),
故答案为:(1,1),(0,4),(2,2);
(2)由题意知,点B旋转到点B1的弧所在的圆的半径为4,弧所对的圆心角为90°,
∴弧长为:=2π.
19.解:(1)∵∠APC=∠CPB=60°,
∴由圆周角定理得:∠ABC=∠APC=60°,∠BAC=∠BPC=60°,
∴∠ACB=180°﹣∠ABC﹣∠BAC=60°;
(2)连结OB,OC,过点O作OD⊥BC于点D,
∵∠BAC=60°,
∴∠BOC=2∠BAC=120°.
∵OD⊥BC于点D,OB=OC,
∴∠BOD=BOC=60°,
BD=BC==3,
∵Rt△BOD中,,
∴,
∴的长=.
20.解:(1)如图1,过点O作OM⊥AC,ON⊥BD,垂足分别为M、N,
∵AC⊥BD,
∴∠MEN=90°=∠ONE=∠OME,
∴四边形OMEN是矩形,
又∵AC=BD,OM⊥AC,ON⊥BD,
∴OM=ON,AM=CM=BN=DN,
∴四边形OMEN是正方形,
∴ME=NE,
∴ME+AM=NE+BN,
即AE=BE,
∴△ABE是等腰直角三角形,
∴∠ABD=45°;
(2)如图2,由(1)可得AM=BN,OM=NE,∠ABD=∠BAC=45°,
∵∠OAB=15°,
∴∠OAM=45°﹣15°=30°,
在Rt△AOM中,∠OAM=30°,OA=2,
∴OM=OA=1,AM=OA=,
∴BE=BN+NE=+1;
(3)如图2,连接OB、OC、OD,
∵OA=OB,∠OAB=15°,
∴∠AOB=180°﹣15°﹣15°=150°,
∵∠ABD=∠BAC=45°,
∴∠AOD=∠BOC=45°×2=90°,
∴∠COD=360°﹣150°﹣90°﹣90°=30°,
∴==.
21.(1)证明:∵∠A=90°,CE⊥BD,
∴∠A=∠BEC=90°.
∵BC∥AD,
∴∠ADB=∠EBC.
∵将斜边BD绕点B顺时针方向旋转至BC,
∴BD=BC.
在△ABD和△ECB中,
∴△ABD≌△ECB;
(2)∵△ABD≌△ECB,
∴AD=BE=3.
∵∠A=90°,∠BAD=30°,
∴BD=2AD=6,
∵BC∥AD,
∴∠A+∠ABC=180°,
∴∠ABC=90°,
∴∠DBC=60°,
∴弧CD的长为=2π.
22.解:(1)∵四边形ABCD内接于圆O,
∴∠DCB+∠BAD=180°,
∵∠A=105°,
∴∠C=180°﹣105°=75°,
∵BD=CD,
∴∠DBC=∠C=75°;
(2)连接BO、CO,
∵∠C=∠DBC=75°,
∴∠BDC=30°,
∴∠BOC=60°,
故的长l==π.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
