三角形内角和定理
图片预览


文档简介
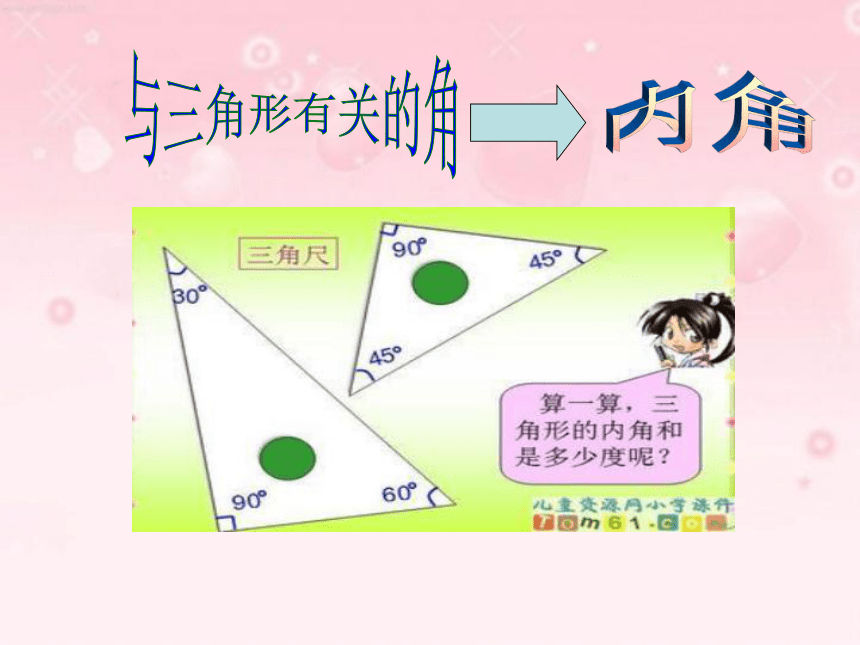
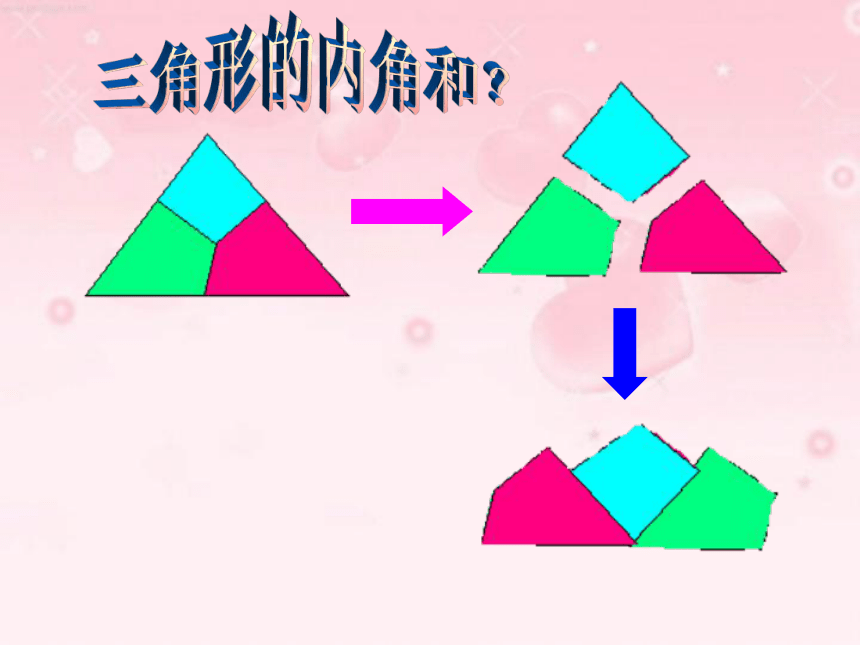
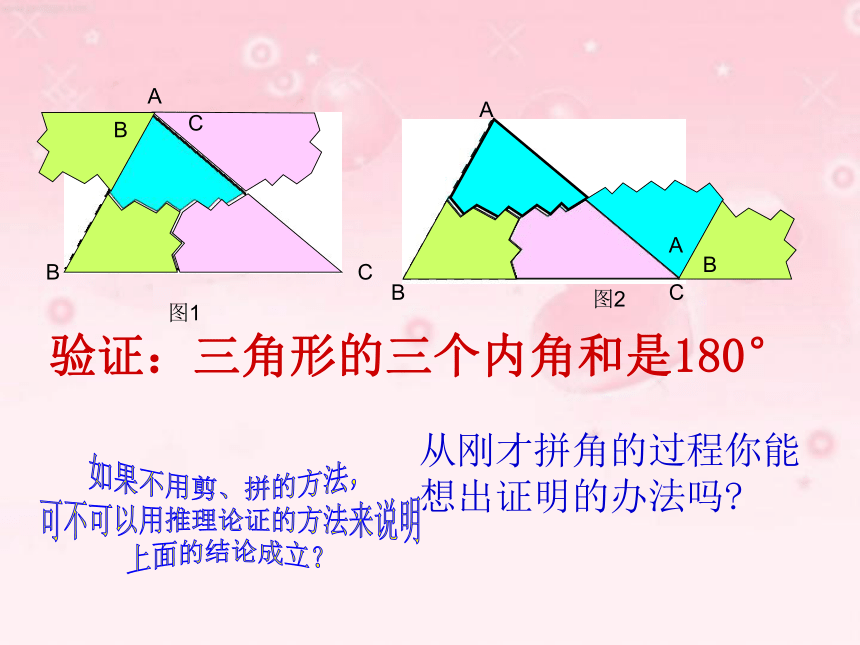
课件22张PPT。三角形内角和定理人教版与三角形有关的角内角三角形的内角和?验证:三角形的三个内角和是180°图1图2ABCABC从刚才拼角的过程你能想出证明的办法吗?如果不用剪、拼的方法,
可不可以用推理论证的方法来说明
上面的结论成立?三角形三个内角的和等于1800条件:三角形的三个内角
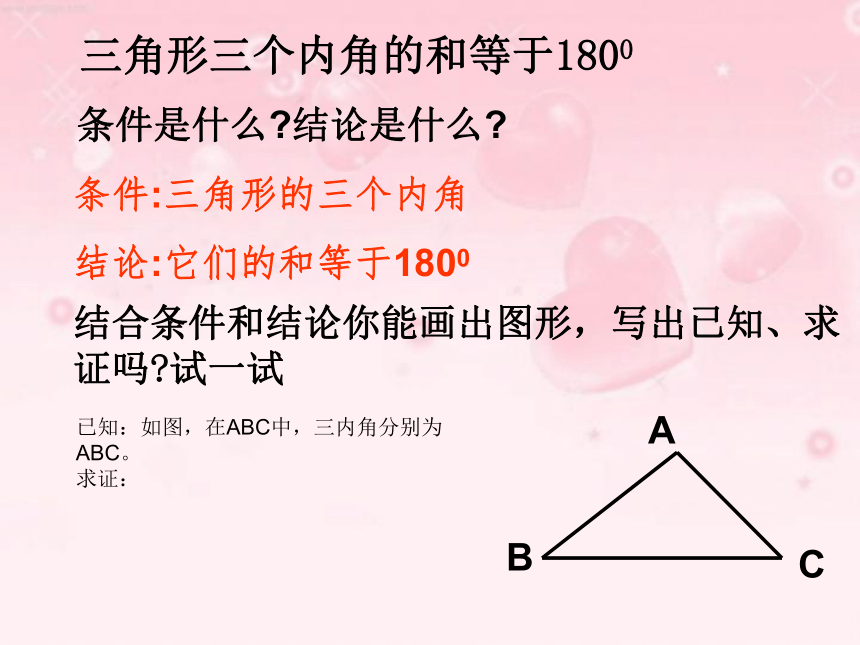
结论:它们的和等于1800结合条件和结论你能画出图形,写出已知、求证吗?试一试
条件是什么?结论是什么?
已知:如图,在ABC中,三内角分别为ABC。
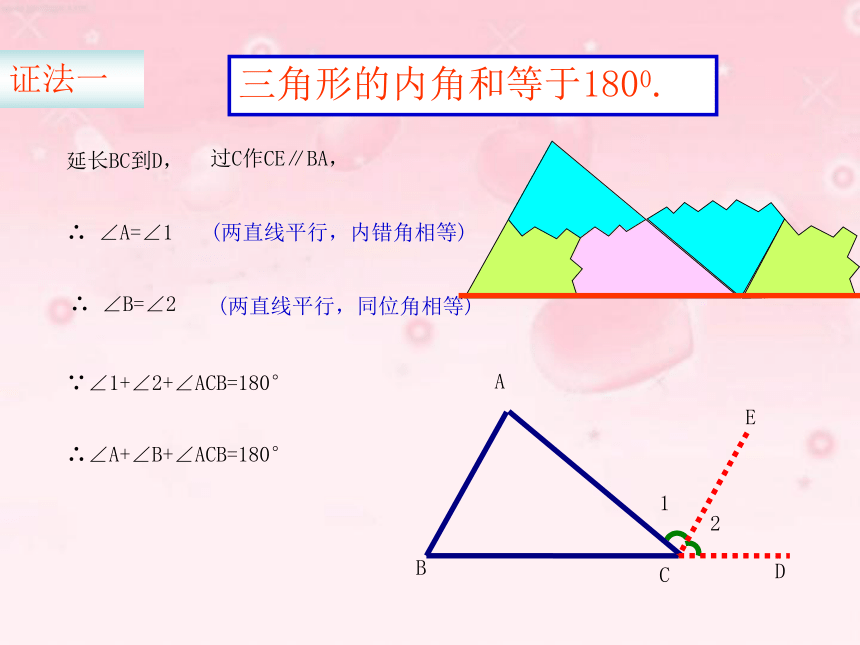
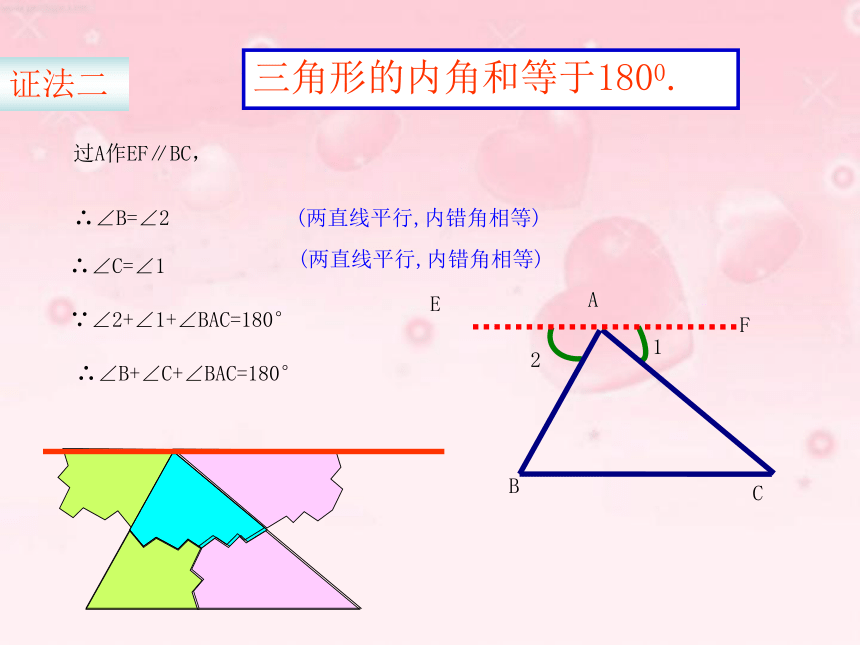
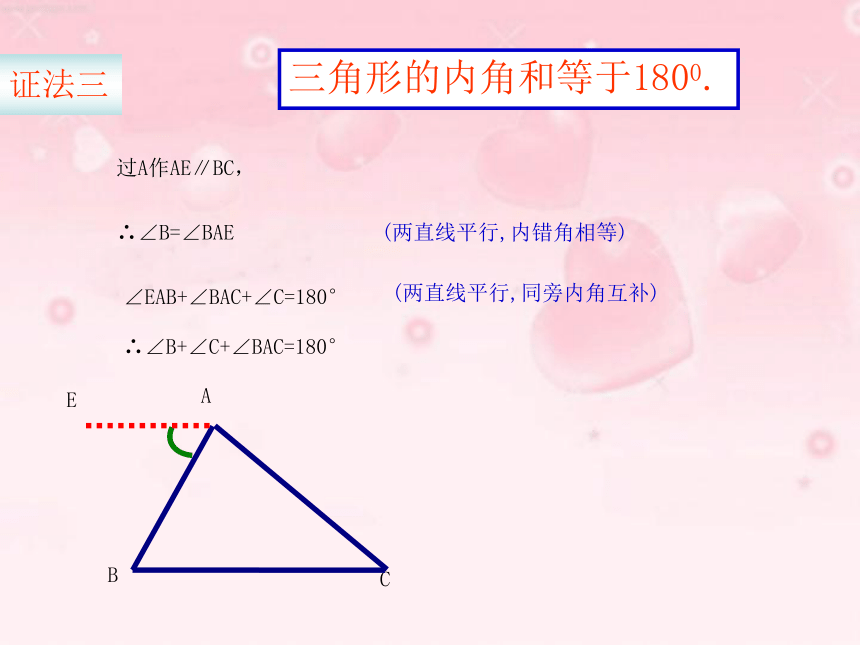
求证:21EDCBA三角形的内角和等于1800.延长BC到D,过C作CE∥BA,∴ ∠A=∠1 (两直线平行,内错角相等)∴ ∠B=∠2(两直线平行,同位角相等)∵∠1+∠2+∠ACB=180°∴∠A+∠B+∠ACB=180°证法一F21ECBA三角形的内角和等于1800.过A作EF∥BC,∴∠B=∠2(两直线平行,内错角相等) ∴∠C=∠1(两直线平行,内错角相等) ∵∠2+∠1+∠BAC=180°∴∠B+∠C+∠BAC=180°证法二CBEA三角形的内角和等于1800.过A作AE∥BC,∴∠B=∠BAE(两直线平行,内错角相等)∠EAB+∠BAC+∠C=180°(两直线平行,同旁内角互补)∴∠B+∠C+∠BAC=180°证法三三角形的内角和等于180°三角形的内角和定理:师生交流:(口答)下列各组角是同一个三角形的内角吗?为什么?(2)60°, 40°, 90°(3)30°, 60°, 50°(1)3°, 150°, 27° (是 )( 不是)( 不是)应用新知(1)在△ABC中,∠A=35°,∠ B=43 °
则∠ C= .
(2)在△ABC中, ∠A :∠B:∠C=2:3:4
则∠A = ∠ B= ∠ C= . (3)一个三角形中最多有 个直角?为什么?
(4)一个三角形中最多有 个钝角?为什么?
(5)一个三角形中至少有 个锐角?为什么?
(6)任意一个三角形中,最大的一个角的度数至少为 .102 °80 °60 °40 °60°211应用新知例1已知:在△ABC中,∠C=∠ABC=2∠A,BD是AC边上 的高, 求∠DBC的度数.分析:∠DBC在△BDC中,∠BDC=900,为求∠DBC的度数,只要求出∠C的度数即可.解:设∠A= x ,则∠C=∠ABC=2x. ∴x+ 2x+ 2x=180(三角形内角和定理).解方程,得x=360.
∴ ∠C=2×360=720.在△BDC中,
∵∠BDC=900(已知),
∴∠DBC=1800-900-720(三角形内角和定理).
∴∠DBC=180.ABCD应用新知例2. 在△ABC中,已知∠A-∠C=250,∠B-∠A=100,求: ∠B的度数.分析:根据三角形内角和定理可知: ∠A+∠B+∠C=
1800,然后结合已知条件便可以求出.解:在△ABC中,
∠A+∠B+∠C=1800(三角形內角和定理)
联立∠A-∠C=250,∠B-∠A=100可得,
∠A=650,∠B=750,∠C=400
答:∠B的度数是750.
1、在△ABC中,如果∠A= ∠B= ∠ C,那么△ABC是什么三角形?解:设∠A=x°,那么∠B=2x°,∠C=3x°根据题意得:练习解得:∴∠A=30°,∠B=60°,∠C=90°所以△ABC是直角三角形2.如图:已知在△ABC中,EF与AC交于点G,与BC
的延长线交于点F,∠B=450 ,∠F=300,∠CGF=700,
求∠A的度数.AEGFCB3. 如图△ABC中,CD平分∠ACB,DE∥BC,
∠A=70°,∠ADE=50°, 求∠BDC的度数.解:∵∠A=70° ∴∠ACB=180 °-∠A-∠B=180°-70°-50°=60°∵DE//BC∴∠B=∠ADE=50°∵ CD平分∠ACB如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。求下面各题.(1)∠DAC=_____ ∠DAB=______ ∠EBC=_______ ∠CAB = ______ A(2)从C岛看A 、B两岛的视角∠C是多少?50°80°40°北解:∵ AD∥BE
∴ ∠DAB﹢∠ABE=180° ∴ ∠ABE = 180°-∠DAB = 180° - 80° =100° 在△ABC中,∠C = 180° - ∠CAB - ∠ABC= 180°-30 °-60 °=90°∴ ∠ABC=∠ABE﹣∠CBE30 °=100°﹣40°=60°例题讲解2DCE北A50°∟B40 °北MN在△AMC中 ∠AMC=90°, ∠MAC=50°解:过点C画MN⊥AD分别交AD、BE于点M、N12例:如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。∴∠1=180 °-90°-50° =40°∵ AD∥BE∴ ∠AMC+ ∠BNC =180 °∴ ∠BNC =90°同理得∠2 =50°∴ ∠ACB =180 ° -∠1 -∠2=180 °-40°-50° =90°例题讲解2B 你能想出一个更简捷的方法来求∠C的度数吗?1250°40°解: 过点C画CF∥AD ∴ ∠1=∠DAC=50 °, F∵ CF∥AD, 又AD ∥BE∴ CF∥ BE∴∠2=∠CBE =40 °∴ ∠ACB=∠1﹢∠2 =50 °﹢ 40 ° =90 °例题讲解2解:在△ACD中 ∠CAD =30 ° ∠D =90 °∴ ∠ACD =180 ° -30 ° -90 °=6 0 °在△BCD中 ∠CBD = 45 ° ∠D =90 ° ∴ ∠BCD = 180 °- 90°-45 °=45 °∴ ∠ACB = ∠ACD - ∠BCD = 6 0 °- 45 °巩固练习1.如图,从A处观测C处时仰角∠CAD=30°,从B处观测C处时仰角∠CBD=45°.从C处观测A、B两处时视角∠ACB是多少?拓展与思考2.甲楼高16米,乙楼座落在甲楼的正北面,已知当地冬至中午12点,太阳光线与水平面夹角为450,如果甲楼的影子刚好不落在乙楼上,那么两楼的距离应是多少?甲乙450?45016米解:由题意知ABC∴BC=AB=16答:两楼的距离是16米.拓展与思考再见
可不可以用推理论证的方法来说明
上面的结论成立?三角形三个内角的和等于1800条件:三角形的三个内角
结论:它们的和等于1800结合条件和结论你能画出图形,写出已知、求证吗?试一试
条件是什么?结论是什么?
已知:如图,在ABC中,三内角分别为ABC。
求证:21EDCBA三角形的内角和等于1800.延长BC到D,过C作CE∥BA,∴ ∠A=∠1 (两直线平行,内错角相等)∴ ∠B=∠2(两直线平行,同位角相等)∵∠1+∠2+∠ACB=180°∴∠A+∠B+∠ACB=180°证法一F21ECBA三角形的内角和等于1800.过A作EF∥BC,∴∠B=∠2(两直线平行,内错角相等) ∴∠C=∠1(两直线平行,内错角相等) ∵∠2+∠1+∠BAC=180°∴∠B+∠C+∠BAC=180°证法二CBEA三角形的内角和等于1800.过A作AE∥BC,∴∠B=∠BAE(两直线平行,内错角相等)∠EAB+∠BAC+∠C=180°(两直线平行,同旁内角互补)∴∠B+∠C+∠BAC=180°证法三三角形的内角和等于180°三角形的内角和定理:师生交流:(口答)下列各组角是同一个三角形的内角吗?为什么?(2)60°, 40°, 90°(3)30°, 60°, 50°(1)3°, 150°, 27° (是 )( 不是)( 不是)应用新知(1)在△ABC中,∠A=35°,∠ B=43 °
则∠ C= .
(2)在△ABC中, ∠A :∠B:∠C=2:3:4
则∠A = ∠ B= ∠ C= . (3)一个三角形中最多有 个直角?为什么?
(4)一个三角形中最多有 个钝角?为什么?
(5)一个三角形中至少有 个锐角?为什么?
(6)任意一个三角形中,最大的一个角的度数至少为 .102 °80 °60 °40 °60°211应用新知例1已知:在△ABC中,∠C=∠ABC=2∠A,BD是AC边上 的高, 求∠DBC的度数.分析:∠DBC在△BDC中,∠BDC=900,为求∠DBC的度数,只要求出∠C的度数即可.解:设∠A= x ,则∠C=∠ABC=2x. ∴x+ 2x+ 2x=180(三角形内角和定理).解方程,得x=360.
∴ ∠C=2×360=720.在△BDC中,
∵∠BDC=900(已知),
∴∠DBC=1800-900-720(三角形内角和定理).
∴∠DBC=180.ABCD应用新知例2. 在△ABC中,已知∠A-∠C=250,∠B-∠A=100,求: ∠B的度数.分析:根据三角形内角和定理可知: ∠A+∠B+∠C=
1800,然后结合已知条件便可以求出.解:在△ABC中,
∠A+∠B+∠C=1800(三角形內角和定理)
联立∠A-∠C=250,∠B-∠A=100可得,
∠A=650,∠B=750,∠C=400
答:∠B的度数是750.
1、在△ABC中,如果∠A= ∠B= ∠ C,那么△ABC是什么三角形?解:设∠A=x°,那么∠B=2x°,∠C=3x°根据题意得:练习解得:∴∠A=30°,∠B=60°,∠C=90°所以△ABC是直角三角形2.如图:已知在△ABC中,EF与AC交于点G,与BC
的延长线交于点F,∠B=450 ,∠F=300,∠CGF=700,
求∠A的度数.AEGFCB3. 如图△ABC中,CD平分∠ACB,DE∥BC,
∠A=70°,∠ADE=50°, 求∠BDC的度数.解:∵∠A=70° ∴∠ACB=180 °-∠A-∠B=180°-70°-50°=60°∵DE//BC∴∠B=∠ADE=50°∵ CD平分∠ACB如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。求下面各题.(1)∠DAC=_____ ∠DAB=______ ∠EBC=_______ ∠CAB = ______ A(2)从C岛看A 、B两岛的视角∠C是多少?50°80°40°北解:∵ AD∥BE
∴ ∠DAB﹢∠ABE=180° ∴ ∠ABE = 180°-∠DAB = 180° - 80° =100° 在△ABC中,∠C = 180° - ∠CAB - ∠ABC= 180°-30 °-60 °=90°∴ ∠ABC=∠ABE﹣∠CBE30 °=100°﹣40°=60°例题讲解2DCE北A50°∟B40 °北MN在△AMC中 ∠AMC=90°, ∠MAC=50°解:过点C画MN⊥AD分别交AD、BE于点M、N12例:如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向。∴∠1=180 °-90°-50° =40°∵ AD∥BE∴ ∠AMC+ ∠BNC =180 °∴ ∠BNC =90°同理得∠2 =50°∴ ∠ACB =180 ° -∠1 -∠2=180 °-40°-50° =90°例题讲解2B 你能想出一个更简捷的方法来求∠C的度数吗?1250°40°解: 过点C画CF∥AD ∴ ∠1=∠DAC=50 °, F∵ CF∥AD, 又AD ∥BE∴ CF∥ BE∴∠2=∠CBE =40 °∴ ∠ACB=∠1﹢∠2 =50 °﹢ 40 ° =90 °例题讲解2解:在△ACD中 ∠CAD =30 ° ∠D =90 °∴ ∠ACD =180 ° -30 ° -90 °=6 0 °在△BCD中 ∠CBD = 45 ° ∠D =90 ° ∴ ∠BCD = 180 °- 90°-45 °=45 °∴ ∠ACB = ∠ACD - ∠BCD = 6 0 °- 45 °巩固练习1.如图,从A处观测C处时仰角∠CAD=30°,从B处观测C处时仰角∠CBD=45°.从C处观测A、B两处时视角∠ACB是多少?拓展与思考2.甲楼高16米,乙楼座落在甲楼的正北面,已知当地冬至中午12点,太阳光线与水平面夹角为450,如果甲楼的影子刚好不落在乙楼上,那么两楼的距离应是多少?甲乙450?45016米解:由题意知ABC∴BC=AB=16答:两楼的距离是16米.拓展与思考再见
