第12章全等三角形复习导学案
文档属性
| 名称 | 第12章全等三角形复习导学案 |  | |
| 格式 | zip | ||
| 文件大小 | 68.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-11 13:46:47 | ||
图片预览


文档简介
全等三角形复习导学案
学习目标:1.了解三角形全等的特征。2、掌握全等三角形的判定方法。
学习重点、难点:全等三角形的判定方法。
学法指导: 自主学习,合作探究
一、问题导入
知识回顾
1. 定义:
___ ____ ______ __ _____ _叫做全等三角形。
2. 基本性质:
全等三角形的_____________________。
3、证明一般两个三角形全等有哪些方法
4、想一想:三角形全等的判定方法共有几种?
注意(1)两边及其一边所对的角相等,两个三角形不一定全等
注意(2)说明两个三角形全等时,特别注意边和角“位置上对应相等” 。
5、判定两个三角形全等必须具备的条件:
SSS—三边对应相等的两个三角形全等;
SAS—两边夹角对应相等的两个三角形全等;
ASA—两角夹边对应相等的两个三角形全等;
AAS—两角和其中一角的对边对应相等的两个三角形全等。
注意:1)三角对应相等的两个三角形不一定全等;
2)两边和其中一边的对角对应相等的两个三角形不一定全等
6、判定三角形全等的口诀
判定全等标条件,对应相等最关键;
边边边,边角边,角边角,角角边;
没有什么边边角,缺一不可条件三。
二、自主探究、合作交流
(一)让你的思维做运动
1、如图AC与BD相交于点O.已知OA=OC,OB=OD.
说明 △AOB≌△COD 的理由
2、已知:如图,∠DAB=∠CAB,∠C=∠D ,则AD=AC,请说明理由。
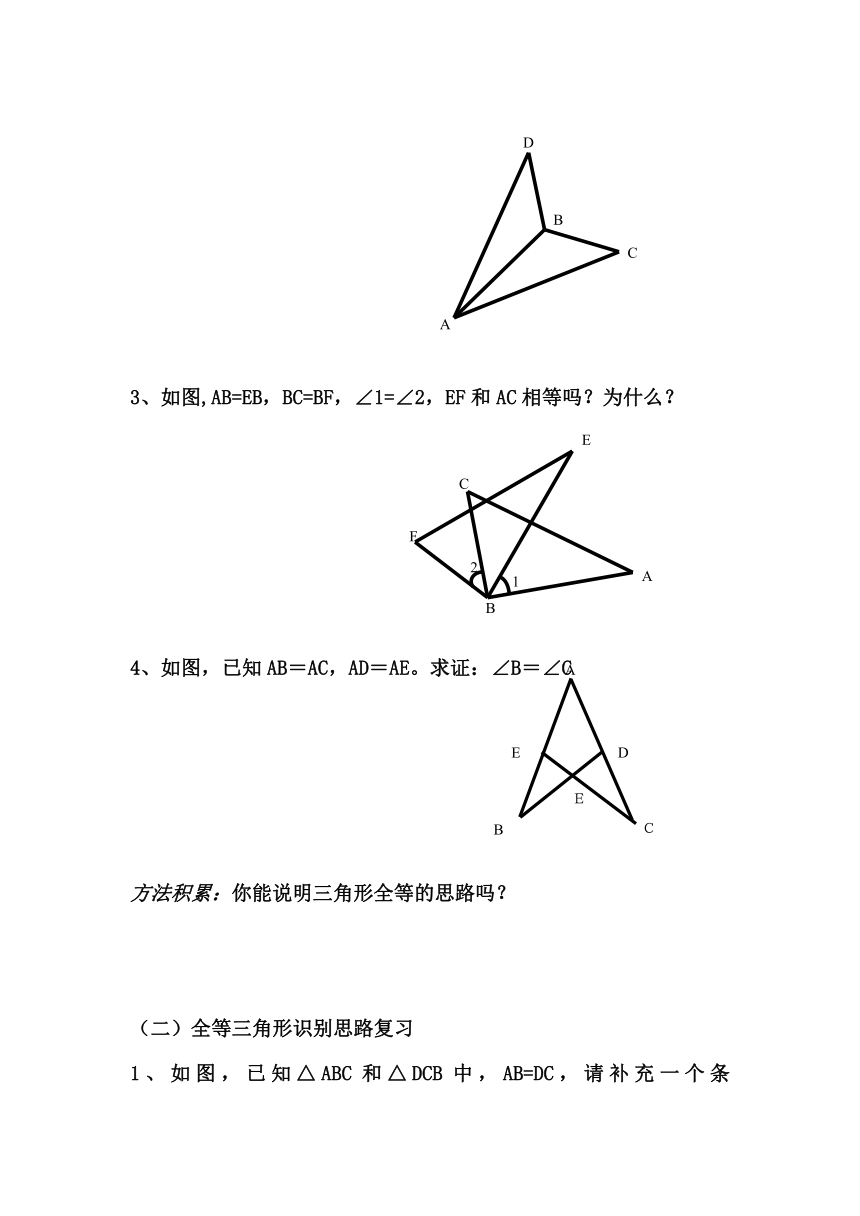
3、如图,AB=EB,BC=BF,∠1=∠2,EF和AC相等吗?为什么?
4、如图,已知AB=AC,AD=AE。求证:∠B=∠C
方法积累:你能说明三角形全等的思路吗?
(二)全等三角形识别思路复习
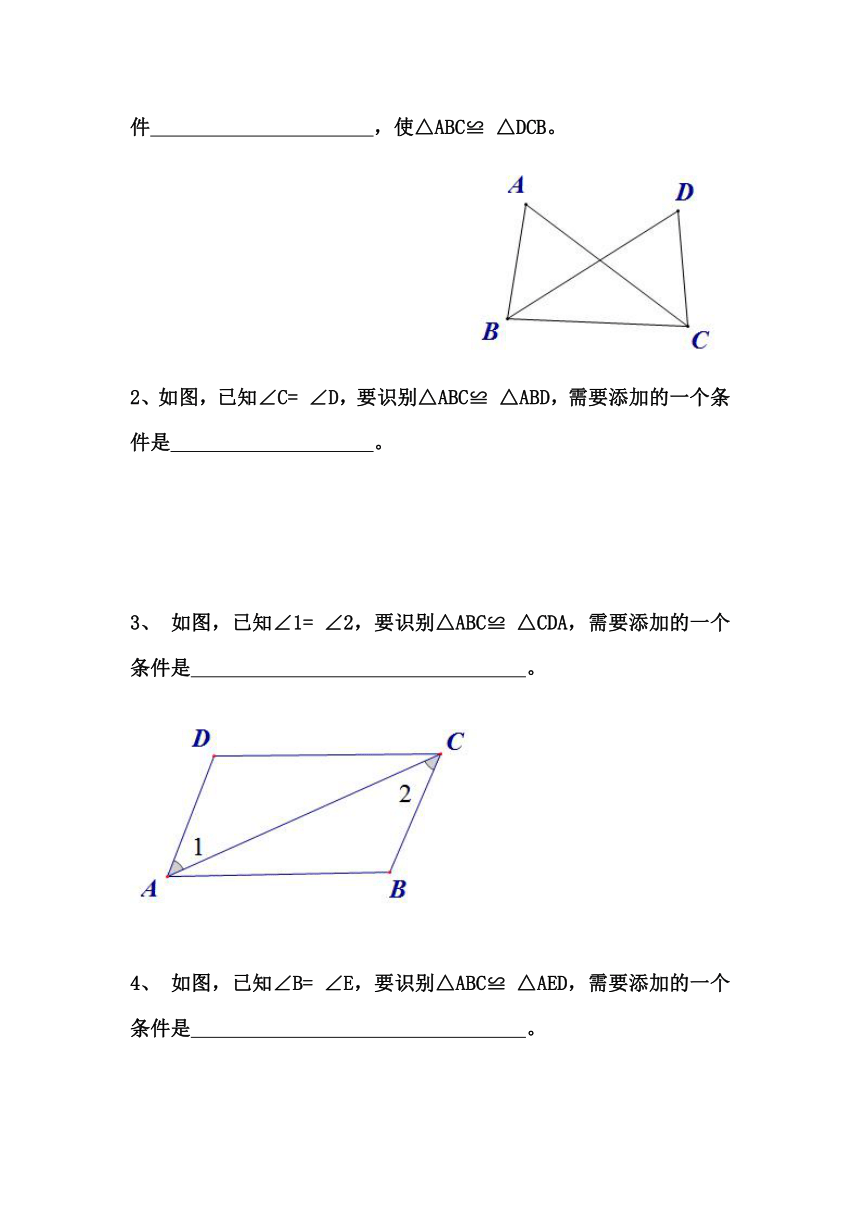
1、如图,已知△ABC和△DCB中,AB=DC,请补充一个条件 ,使△ABC≌ △DCB。
2、如图,已知∠C= ∠D,要识别△ABC≌ △ABD,需要添加的一个条件是 。
3、 如图,已知∠1= ∠2,要识别△ABC≌ △CDA,需要添加的一个条件是 。
4、 如图,已知∠B= ∠E,要识别△ABC≌ △AED,需要添加的一个条件是 。
三、学以致用
1.如图,AE=CF,∠AFD=∠CEB,DF=BE,△AFD与△ CEB全等吗?为什么?
2.如图(5)∠CAE=∠BAD,∠B=∠D,AC=AE,△ABC与△ADE全等吗?
为什么?
3.“三月三,放风筝”如图,是小东同学自己做的风筝,他根据AB=AD,BC=DC,不用度量,就知道∠ABC=∠ADC。请用所学的知识给予说明。
四、探索编拟问题型
例:如图,在△AFD和△BEC中,点A、E、F、C在同一直线上,有下列四个论断: ①AD=CB,②AE=CF,③∠B=∠D,④ ∠A=∠C.请用其中三个作为条件,余下一个作为结论,编一道数学问题,并写出解答过程。
五、课堂小结:(由学生回顾本节课所学内容,谈谈自己的收获与体会)
六、当堂检测
1、如图,∠ ABC=∠ DCB,∠ ACB=∠ DBC,试说明△ ABC≌ △ DCB
2、如图,已知AB与CD相交于点O,AO=BO,∠A=∠B,
说明△AOC与△BOD全等的理由。
3、已知AB=AC,∠B=∠C,说明△ABD≌△ACE的理由
4、拓展提高:
如图,已知AB⊥BD,ED⊥BD,AB=CD,BC=DE 请说明△ABC ≌△CDE,并判断AC是否垂直CE?
A
B
C
D
C
E
F
B
A
1
2
A
D
B
E
C
E
A
B
D
C
A
B
C
D
E
学习目标:1.了解三角形全等的特征。2、掌握全等三角形的判定方法。
学习重点、难点:全等三角形的判定方法。
学法指导: 自主学习,合作探究
一、问题导入
知识回顾
1. 定义:
___ ____ ______ __ _____ _叫做全等三角形。
2. 基本性质:
全等三角形的_____________________。
3、证明一般两个三角形全等有哪些方法
4、想一想:三角形全等的判定方法共有几种?
注意(1)两边及其一边所对的角相等,两个三角形不一定全等
注意(2)说明两个三角形全等时,特别注意边和角“位置上对应相等” 。
5、判定两个三角形全等必须具备的条件:
SSS—三边对应相等的两个三角形全等;
SAS—两边夹角对应相等的两个三角形全等;
ASA—两角夹边对应相等的两个三角形全等;
AAS—两角和其中一角的对边对应相等的两个三角形全等。
注意:1)三角对应相等的两个三角形不一定全等;
2)两边和其中一边的对角对应相等的两个三角形不一定全等
6、判定三角形全等的口诀
判定全等标条件,对应相等最关键;
边边边,边角边,角边角,角角边;
没有什么边边角,缺一不可条件三。
二、自主探究、合作交流
(一)让你的思维做运动
1、如图AC与BD相交于点O.已知OA=OC,OB=OD.
说明 △AOB≌△COD 的理由
2、已知:如图,∠DAB=∠CAB,∠C=∠D ,则AD=AC,请说明理由。
3、如图,AB=EB,BC=BF,∠1=∠2,EF和AC相等吗?为什么?
4、如图,已知AB=AC,AD=AE。求证:∠B=∠C
方法积累:你能说明三角形全等的思路吗?
(二)全等三角形识别思路复习
1、如图,已知△ABC和△DCB中,AB=DC,请补充一个条件 ,使△ABC≌ △DCB。
2、如图,已知∠C= ∠D,要识别△ABC≌ △ABD,需要添加的一个条件是 。
3、 如图,已知∠1= ∠2,要识别△ABC≌ △CDA,需要添加的一个条件是 。
4、 如图,已知∠B= ∠E,要识别△ABC≌ △AED,需要添加的一个条件是 。
三、学以致用
1.如图,AE=CF,∠AFD=∠CEB,DF=BE,△AFD与△ CEB全等吗?为什么?
2.如图(5)∠CAE=∠BAD,∠B=∠D,AC=AE,△ABC与△ADE全等吗?
为什么?
3.“三月三,放风筝”如图,是小东同学自己做的风筝,他根据AB=AD,BC=DC,不用度量,就知道∠ABC=∠ADC。请用所学的知识给予说明。
四、探索编拟问题型
例:如图,在△AFD和△BEC中,点A、E、F、C在同一直线上,有下列四个论断: ①AD=CB,②AE=CF,③∠B=∠D,④ ∠A=∠C.请用其中三个作为条件,余下一个作为结论,编一道数学问题,并写出解答过程。
五、课堂小结:(由学生回顾本节课所学内容,谈谈自己的收获与体会)
六、当堂检测
1、如图,∠ ABC=∠ DCB,∠ ACB=∠ DBC,试说明△ ABC≌ △ DCB
2、如图,已知AB与CD相交于点O,AO=BO,∠A=∠B,
说明△AOC与△BOD全等的理由。
3、已知AB=AC,∠B=∠C,说明△ABD≌△ACE的理由
4、拓展提高:
如图,已知AB⊥BD,ED⊥BD,AB=CD,BC=DE 请说明△ABC ≌△CDE,并判断AC是否垂直CE?
A
B
C
D
C
E
F
B
A
1
2
A
D
B
E
C
E
A
B
D
C
A
B
C
D
E
