华师大版九年级上册23.4中位线 课件(共20张PPT)
文档属性
| 名称 | 华师大版九年级上册23.4中位线 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-17 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
第23章图形的相似
23.4 中位线
第23章 图形的相似
学 习 目 标
理解三角形中位线的定义,掌握三角形中位线定理.(重点)
通过探索,猜想,证明三角形的中位线定理,进一
步发展推理论证的能力.
经历三角形中位线的性质定理及重心的推导过程;(难点)
1
2
3
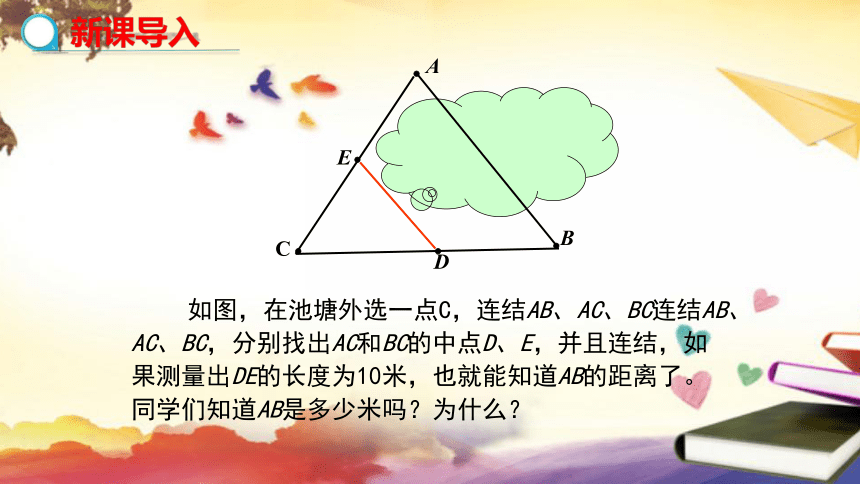
如图,在池塘外选一点C,连结AB、AC、BC连结AB、AC、BC,分别找出AC和BC的中点D、E,并且连结,如果测量出DE的长度为10米,也就能知道AB的距离了。同学们知道AB是多少米吗?为什么?
D
E
B
A
C
新课导入
知识讲解
请同学们按要求画图:
在任意△ABC中,取AB、AC边中点D、E,
连接DE.
D
E
定义:像DE这样,连结三角形两边中点的线段叫做三角形的中位线.
1
三角形的中位线
探究思考
问题1:
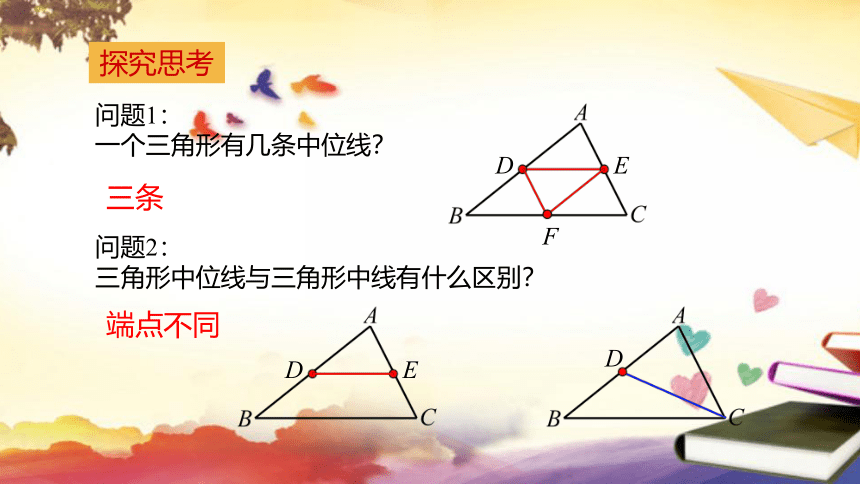
一个三角形有几条中位线?
D
E
F
三条
问题2:
三角形中位线与三角形中线有什么区别?
D
E
D
端点不同
探究思考
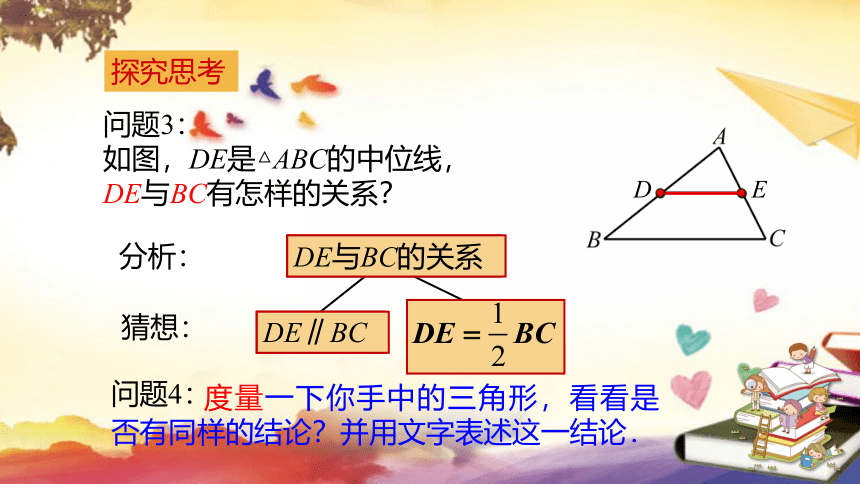
问题3:
如图,DE是△ABC的中位线,
DE与BC有怎样的关系?
D
E
两条线段的关系
位置关系
数量关系
分析:
DE与BC的关系
猜想:
DE∥BC
?
度量一下你手中的三角形,看看是否有同样的结论?并用文字表述这一结论.
问题4:
探究思考
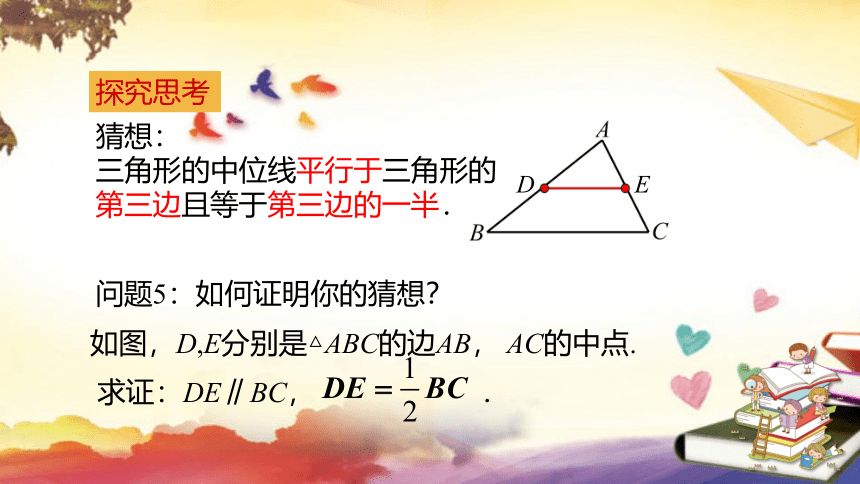
猜想:
三角形的中位线平行于三角形的
第三边且等于第三边的一半.
D
E
问题5:如何证明你的猜想?
如图,D,E分别是△ABC的边AB, AC的中点.
求证:DE∥BC, .
证明:
D
E
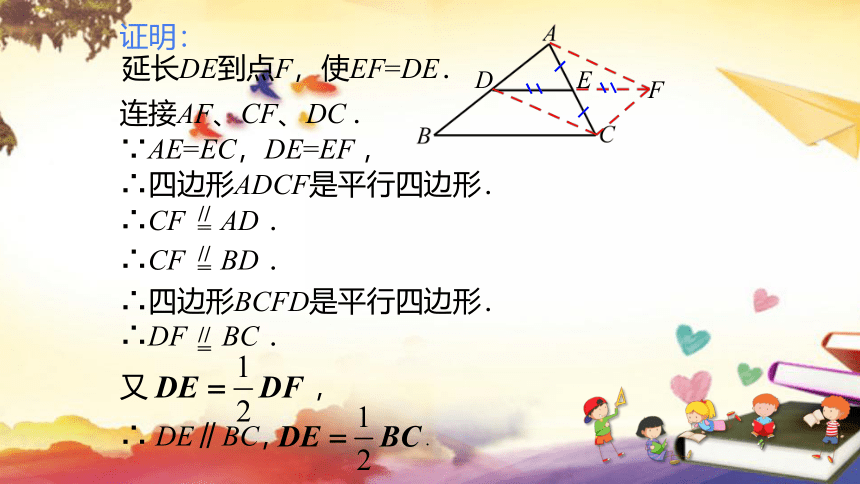
延长DE到点F,使EF=DE.
连接AF、CF、DC .
∵AE=EC,DE=EF ,
∴四边形ADCF是平行四边形.
F
∴四边形BCFD是平行四边形.
∴CF AD .
∴CF BD .
∴ DE∥BC, .
又 ,
∴DF BC .
三角形的中位线平行于三角形的
第三边且等于第三边的一半.
D
E
在△ABC中,若D、E分别是边AB、AC的中点,
则DE∥BC,DE= BC.
符号语言:
2
三角形的中位线定理
例1
求证:顺次连结四边形四条边的中点所得的四边形是
平行四边形.
已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
证明:连结AC.
∵AH=HD,CG=GD ,
∴HG∥AC, HG= AC.
同理 EF∥AC, EF= AC,
∴HG∥EF ,HG=EF,
∴四边形EFGH是平行四边形.
例2 如图,△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G.求证: .
证明:连结ED.
∵ D、E分别是边BC、AB的中点,
∴ DE∥AC,
∴ △ACG∽△DEG,
∴
∴
2
三角形的重心
如果在上图中,取AC的中点F,假设BF与AD交于G′ ,如图,那么我们同理可得 ,所以有 ,即两图中的点G与G′是重合的.
于是我们有以下结论:
三角形三条边上的中线交于一点,
这个点就是三角形的重心,重心与一边
中点的连线的长是对应中线长的 .
随堂训练
1、如图,在△ABC中,D、E分别是AB、AC的中点,BC=10cm,则DE=______.
2、如图,在△ABC中,D、E分别是AB、AC的中点,∠A=50°, ∠B=70°,
则∠AED=_____.
5cm
60°
3.如图,在△ABC中,∠C=90°,AC=8,CB=6,D,
E,F分别是BC,AC,AB的中点,则四边形AEDF的周
长为________;Rt△ABC的中位线分别是___________;
斜边上的中线是_______,其长为______.
18
DE,DF
CF
5
A
B
C
D
E
F
4、在△ABC中,D、E、F分别是AB、BC、CA的中点.以这些点为顶点,在图中,你能画出多少个平行四边形?为什么?
A
D
C
B
F
E
解:3个.
平行四边形DFCE,
平行四边形DFEB,
平行四边形DEFA.
5. 如图,A、B两点被池塘隔开,在AB外选一点
C,连结AC和BC,怎样量出A、B两点间的距离?
根据是什么?
解:分别找出AC、BC中点M、N,
量出M、N两点间距离,则AB=2MN.
N
M
根据是三角形中位线定理.
1.三角形的中位线定义:连结三角形两边中点的线段叫做三角形的中位线.
2.三角形的中位线性质:三角形的中位线平行于第三边,并且等于第三边的一半.
3. 三角形的重心:三角形三条边上的中线交于一点,这个点就是三角形的重心.
4. 三角形的重心性质:重心与一边中点的连线的长是对应中线长的 .
课堂小结
教科书第79页练习第1-2题.
习题23.4第1-4题
布 置 作 业
第23章图形的相似
23.4 中位线
第23章 图形的相似
学 习 目 标
理解三角形中位线的定义,掌握三角形中位线定理.(重点)
通过探索,猜想,证明三角形的中位线定理,进一
步发展推理论证的能力.
经历三角形中位线的性质定理及重心的推导过程;(难点)
1
2
3
如图,在池塘外选一点C,连结AB、AC、BC连结AB、AC、BC,分别找出AC和BC的中点D、E,并且连结,如果测量出DE的长度为10米,也就能知道AB的距离了。同学们知道AB是多少米吗?为什么?
D
E
B
A
C
新课导入
知识讲解
请同学们按要求画图:
在任意△ABC中,取AB、AC边中点D、E,
连接DE.
D
E
定义:像DE这样,连结三角形两边中点的线段叫做三角形的中位线.
1
三角形的中位线
探究思考
问题1:
一个三角形有几条中位线?
D
E
F
三条
问题2:
三角形中位线与三角形中线有什么区别?
D
E
D
端点不同
探究思考
问题3:
如图,DE是△ABC的中位线,
DE与BC有怎样的关系?
D
E
两条线段的关系
位置关系
数量关系
分析:
DE与BC的关系
猜想:
DE∥BC
?
度量一下你手中的三角形,看看是否有同样的结论?并用文字表述这一结论.
问题4:
探究思考
猜想:
三角形的中位线平行于三角形的
第三边且等于第三边的一半.
D
E
问题5:如何证明你的猜想?
如图,D,E分别是△ABC的边AB, AC的中点.
求证:DE∥BC, .
证明:
D
E
延长DE到点F,使EF=DE.
连接AF、CF、DC .
∵AE=EC,DE=EF ,
∴四边形ADCF是平行四边形.
F
∴四边形BCFD是平行四边形.
∴CF AD .
∴CF BD .
∴ DE∥BC, .
又 ,
∴DF BC .
三角形的中位线平行于三角形的
第三边且等于第三边的一半.
D
E
在△ABC中,若D、E分别是边AB、AC的中点,
则DE∥BC,DE= BC.
符号语言:
2
三角形的中位线定理
例1
求证:顺次连结四边形四条边的中点所得的四边形是
平行四边形.
已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
证明:连结AC.
∵AH=HD,CG=GD ,
∴HG∥AC, HG= AC.
同理 EF∥AC, EF= AC,
∴HG∥EF ,HG=EF,
∴四边形EFGH是平行四边形.
例2 如图,△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G.求证: .
证明:连结ED.
∵ D、E分别是边BC、AB的中点,
∴ DE∥AC,
∴ △ACG∽△DEG,
∴
∴
2
三角形的重心
如果在上图中,取AC的中点F,假设BF与AD交于G′ ,如图,那么我们同理可得 ,所以有 ,即两图中的点G与G′是重合的.
于是我们有以下结论:
三角形三条边上的中线交于一点,
这个点就是三角形的重心,重心与一边
中点的连线的长是对应中线长的 .
随堂训练
1、如图,在△ABC中,D、E分别是AB、AC的中点,BC=10cm,则DE=______.
2、如图,在△ABC中,D、E分别是AB、AC的中点,∠A=50°, ∠B=70°,
则∠AED=_____.
5cm
60°
3.如图,在△ABC中,∠C=90°,AC=8,CB=6,D,
E,F分别是BC,AC,AB的中点,则四边形AEDF的周
长为________;Rt△ABC的中位线分别是___________;
斜边上的中线是_______,其长为______.
18
DE,DF
CF
5
A
B
C
D
E
F
4、在△ABC中,D、E、F分别是AB、BC、CA的中点.以这些点为顶点,在图中,你能画出多少个平行四边形?为什么?
A
D
C
B
F
E
解:3个.
平行四边形DFCE,
平行四边形DFEB,
平行四边形DEFA.
5. 如图,A、B两点被池塘隔开,在AB外选一点
C,连结AC和BC,怎样量出A、B两点间的距离?
根据是什么?
解:分别找出AC、BC中点M、N,
量出M、N两点间距离,则AB=2MN.
N
M
根据是三角形中位线定理.
1.三角形的中位线定义:连结三角形两边中点的线段叫做三角形的中位线.
2.三角形的中位线性质:三角形的中位线平行于第三边,并且等于第三边的一半.
3. 三角形的重心:三角形三条边上的中线交于一点,这个点就是三角形的重心.
4. 三角形的重心性质:重心与一边中点的连线的长是对应中线长的 .
课堂小结
教科书第79页练习第1-2题.
习题23.4第1-4题
布 置 作 业
