2022-2023学年新高一上学期数学沪教版(2020)摸底测试练习卷【3】(Word含解析)
文档属性
| 名称 | 2022-2023学年新高一上学期数学沪教版(2020)摸底测试练习卷【3】(Word含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 709.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-15 20:48:30 | ||
图片预览




文档简介
【学生版】
【沪教版2020】高中数学 新高一 摸底测试练习卷【3】
考生注意:
1.本试卷含三个大题,共21题.答题时,考生务必按答题要求在答题纸规定的位置上作答;
2.解答题必须写在试卷题号对应的区域相应位置,并写出解题的主要步骤;
一、填空题(本大题共12题,满分54分,第1~6题每题4分,第7~12题每题5分)考生应在答题纸相应编号的空格内直接填写结果.
1、计算: .
2、式子有意义的的取值范围是
3、设,,,则,,从小到大的顺序是
4、如图,数轴上,两点对应的数分别是和,对于以下四个式子:①;②;③:④,其中值为负数的是
5、如图,传送带的一个转动轮的半径为18cm,转动轮转n°,传送带上的物品A被传送12πcm,则n= .
6、图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空余的部分的面积是
7、随着某地公交票制票价调整,公交集团更换了新版公交站票,乘客在乘车时可以通过新版公交站牌计算乘车费用,新版站牌每一个站名上方都有一个相应的数字,将上下车站站名称对应数字相减取绝对值就是乘车路程,再按照其所在计价区段,参考票制规则计算票价,具体来说:
乘车路程计价区段
对应票价(元 2 3 4
另外,一卡通刷卡实行5折优惠,小明用一卡通乘车上车时站名上对应的数字是5,下车时站名上对应的数字
是22,那么小明乘车的费用是 元
8、某快餐店销售A、B两种快餐,每份利润分别为12元、8元,每天卖出份数分别为40份、80份.该店为了增加利润,准备降低每份A种快餐的利润,同时提高每份B种快餐的利润.售卖时发现,在一定范围内,每份A种快餐利润每降1元可多卖2份,每份B种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变,那么这两种快餐一天的总利润最多是 元.
9、小淇将展开后得到,小尧将展开后得到,若两人计算过程无误,则的值为
10、古希腊数学家把1,3,6,10,15,21,…这样的数叫做三角形数,因为它的规律性可以用如图表示.根据图形,若把第一个图形表示的三角形数记为a1=1,第二个图形表示的三角形数记为a2=3,…,则第n个图形表示的三角形数an= .(用含n的式子表达)
11、如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=2;
以点C为圆心,CB长为半径画弧,
分别交AC,AB于点D,E,
则图中阴影部分的面积为 (结果保留π).
12、我国古代数学的许多创新和发展都位居世界前列,如南宋数宁家杨辉(约13世纪)所著的《详解九章算术》一书中,用下图的三角形解释二项和的展开式的各项系数,此三角形称为“杨辉三角”.
①
①①
①②①
①③③①
①④⑥④①
①⑤⑩⑩⑤①
根据“杨辉三角”请计算的展开式中第三项的系数为
二、选择题(本大题共有4 题,满分20 分,每题5 分)每题有且只有一个正确答案,考生应在答题纸的相应位置,将代表正确选项的小方格涂黑.
13、当时,、、、之间的大小关系是
A. B. C. D.
14、二十四节气,是我国古人根据地球在黄道(即地球绕太阳公转的轨道)上的位置变化而制定的,每一个节气分别相对应于地球在黄道上每运转所到达的一定位置,反映了太阳对地球产生的影响.它凝聚着中华文明的历史文化精华,在国际气象界,二十四节气被誉为“中国的第五大发明”.如图是地球绕太阳公转的轨道图,若将其近似看作圆形,其半径为,则从每年的立春到立夏,地球绕太阳公转的路程是
A. B. C. D.
15、为了了解三中九年级840名学生的体重情况,从中抽取100名学生的体重进行分析.在这项调查中,样本是指( )
A.840名学生
B.被抽取的100名学生
C.840名学生的体重
D.被抽取的100名学生的体重
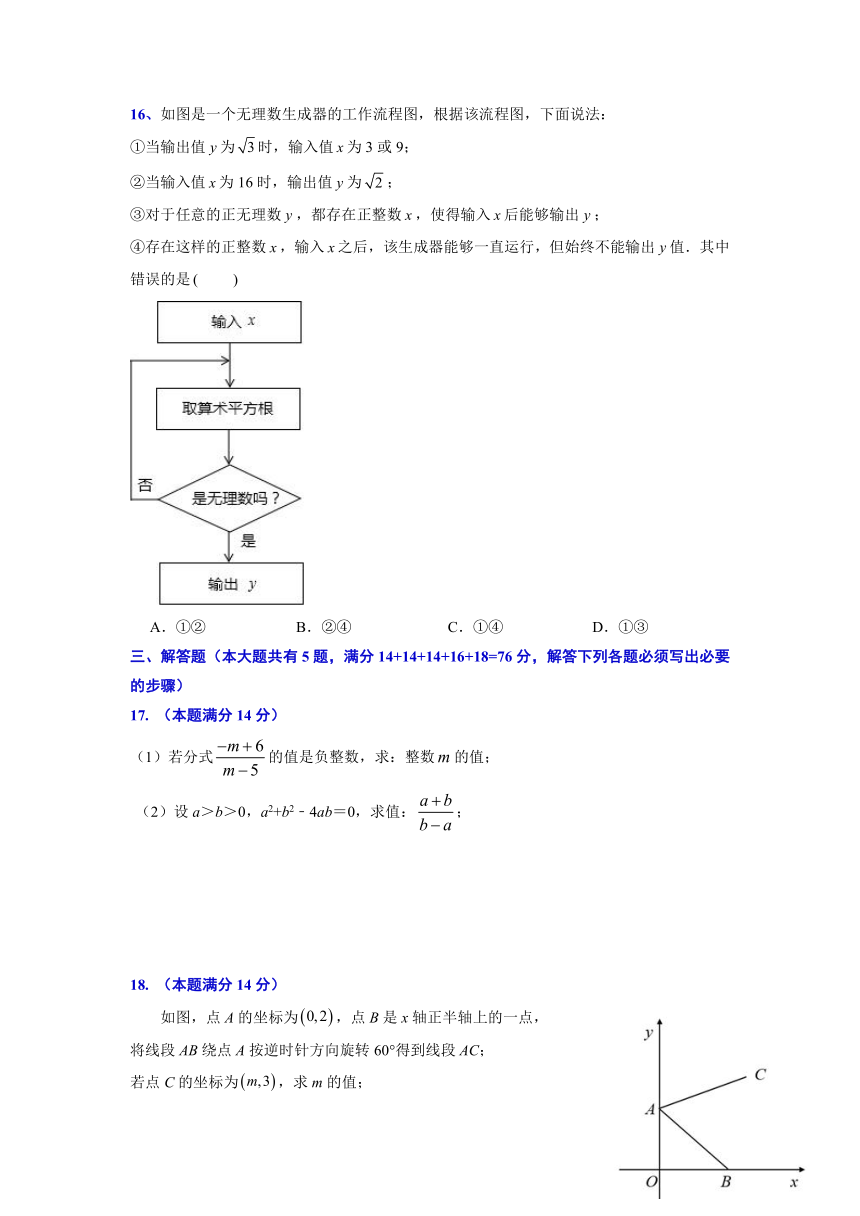
16、如图是一个无理数生成器的工作流程图,根据该流程图,下面说法:
①当输出值为时,输入值为3或9;
②当输入值为16时,输出值为;
③对于任意的正无理数,都存在正整数,使得输入后能够输出;
④存在这样的正整数,输入之后,该生成器能够一直运行,但始终不能输出值.其中错误的是
A.①② B.②④ C.①④ D.①③
三、解答题(本大题共有5题,满分14+14+14+16+18=76分,解答下列各题必须写出必要的步骤)
17. (本题满分14分)
(1)若分式的值是负整数,求:整数的值;
(2)设a>b>0,a2+b2﹣4ab=0,求值:;
18. (本题满分14分)
如图,点A的坐标为,点B是x轴正半轴上的一点,
将线段AB绕点A按逆时针方向旋转60°得到线段AC;
若点C的坐标为,求m的值;
19. (本题满分14分)
如图,AB是⊙O的弦,AB=2,点C是⊙O上的一个动点,
且∠ACB=60°,若点M,N分别是AB,BC的中点,
求图中阴影部分面积的最大值;
20. (本题满分16分)
如图,在△ABC中,BA=BC,D在边CB上,且DB=DA=AC.
(1)如图1,填空∠B= °,∠C= °;
(2)若M为线段BC上的点,过M作直线MH⊥AD于H,分别交直线AB、AC与点N、E,如图2
①求证:△ANE是等腰三角形;
②试写出线段BN、CE、CD之间的数量关系,并加以证明.
21. (本题满分18分)
观察以下等式:
第1个等式:(x﹣1)(x+1)=x2﹣1;
第2个等式:(x﹣1)(x2+x+1)=x3﹣1
第3个等式:(x﹣1)(x3+x2+x+1)=x4﹣1:…
按照以上规律,解决下列问题:
(1)写出第4个等式:(x﹣1)(x4+x3+x2+x+1)= ;
(2)写出你猜想的第n个等式:(x﹣1)(xn+xn﹣1+…+x+1)= ;
(3)请利用上述规律,确定22019+22018+…+2+1的个位数字是多少?
【教师版】
【沪教版2020】高中数学 新高一 摸底测试练习卷【3】
考生注意:
1.本试卷含三个大题,共21题.答题时,考生务必按答题要求在答题纸规定的位置上作答;
2.解答题必须写在试卷题号对应的区域相应位置,并写出解题的主要步骤;
一、填空题(本大题共12题,满分54分,第1~6题每题4分,第7~12题每题5分)考生应在答题纸相应编号的空格内直接填写结果.
1、计算: .
【提示】同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加.据此计算即可.
【答案】
【解析】,故答案为:.
【说明】本题考查了同底数幂的乘法,掌握幂的运算法则是解答本题的关键.
2、式子有意义的的取值范围是
【提示】根据分式有意义,二次根式有意义的条件进行判断即可;
【答案】x≥﹣1且x≠0;
【解析】由题意得,x+1≥0且x≠0,即x≥﹣1且x≠0,
【说明】本题考查二次根式、分式有意义的条件,掌握被开方数大于或等于0,分母不为0分别是二次根式和分式意义的条件是正确判断的前提;
3、设,,,则,,从小到大的顺序是
【提示】将c分母有理化再进行比较即可
【答案】 a<c<b
【解析】由
又由;
又∵a2=()2=7+2,c2=()2=5+2,且,∴a2<c2,
∴a<c,∴a<c<b.故答案为a<c<b.
【说明】本题考查了分母有理化,找到有理化因式是解题的关键.
4、如图,数轴上,两点对应的数分别是和,对于以下四个式子:①;②;③:④,其中值为负数的是
【提示】根据图示,可得,,据此逐项判断即可.
【答案】②④
【解析】根据图示,可得,,①;②;③;④.
故其中值为负数的是②④.
【说明】此题主要考查了绝对值的含义和求法,以及数轴的特征和应用,要熟练掌握,解答此题的关键是判断出、的取值范围;
5、如图,传送带的一个转动轮的半径为18cm,转动轮转n°,传送带上的物品A被传送12πcm,则n= .
【提示】数形结合地分析
【答案】120°
【解析】∵物品A被传送的距离等于转动了n°的弧长,∴=12π,
解得:n=120°,答案:120°.
【说明】熟悉弧长公式;
6、图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空余的部分的面积是
【提示】中间部分的四边形是正方形,表示出边长,则面积可以求得.
【答案】(a﹣b)2
【解析】中间部分的四边形是正方形,边长是a+b﹣2b=a﹣b,则面积是(a﹣b)2
【说明】本题考查了列代数式,正确表示出小正方形的边长是关键.
7、随着某地公交票制票价调整,公交集团更换了新版公交站票,乘客在乘车时可以通过新版公交站牌计算乘车费用,新版站牌每一个站名上方都有一个相应的数字,将上下车站站名称对应数字相减取绝对值就是乘车路程,再按照其所在计价区段,参考票制规则计算票价,具体来说:
乘车路程计价区段
对应票价(元 2 3 4
另外,一卡通刷卡实行5折优惠,小明用一卡通乘车上车时站名上对应的数字是5,下车时站名上对应的数字
是22,那么小明乘车的费用是 元
【提示】首先用下车时站名上对应的数字减去上车时站名上对应的数字,求出小明乘车的路程是多少,进而求出相应的票价是多少;然后用它乘以0.5,求出小明乘车的费用是多少元即可.
【答案】2
【解析】因为小明乘车的路程是:,所以小明乘车的费用是:(元;.
【说明】此题主要考查了有理数的混合运算,要熟练掌握有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算,解答此题的关键是求出小明乘车的路程、相应的票价是多少;
8、某快餐店销售A、B两种快餐,每份利润分别为12元、8元,每天卖出份数分别为40份、80份.该店为了增加利润,准备降低每份A种快餐的利润,同时提高每份B种快餐的利润.售卖时发现,在一定范围内,每份A种快餐利润每降1元可多卖2份,每份B种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变,那么这两种快餐一天的总利润最多是 元.
【提示】注意阅读理解转化;
【答案】1264
【解析】设每份A种快餐降价a元,则每天卖出(40+2a)份,每份B种快餐提高b元,
则每天卖出(80﹣2b)份,
由题意可得,40+2a+80﹣2b=40+80,解得a=b,
∴总利润W=(12﹣a)(40+2a)+(8+a)(80﹣2a)
=﹣4a2+48a+1120=﹣4(a﹣6)2+1264,
∵﹣4<0,∴当a=6时,W取得最大值1264,
即两种快餐一天的总利润最多为1264元.
答案:1264.
9、小淇将展开后得到,小尧将展开后得到,若两人计算过程无误,则的值为
【提示】根据完全平方公式展开求出,,根据平方差公式求值即可.
【答案】4043
【解答】解:展开后得到,,
展开后得到,,
.
【说明】本题考查了完全平方公式,平方差公式,掌握,是解题的关键.
10、古希腊数学家把1,3,6,10,15,21,…这样的数叫做三角形数,因为它的规律性可以用如图表示.根据图形,若把第一个图形表示的三角形数记为a1=1,第二个图形表示的三角形数记为a2=3,…,则第n个图形表示的三角形数an= .(用含n的式子表达)
【答案】
【解析】第1个图形表示的三角形数为1,
第2个图形表示的三角形数为1+2=3,
第3个图形表示的三角形数为1+2+3=6,
第4个图形表示的三角形数为1+2+3+4=10,
.....
第n个图形表示的三角形数为1+2+3+4+......+(n﹣1)+n=;
11、如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=2;
以点C为圆心,CB长为半径画弧,
分别交AC,AB于点D,E,
则图中阴影部分的面积为 (结果保留π).
【提示】注意图像的分割与拼接
【答案】
【解析】连接CE,
∵∠A=30°,
∴∠CBA=90°﹣∠A=60°,
∵CE=CB,
∴△CBE为等边三角形,
∴∠ECB=60°,BE=BC=2,
∴S扇形CBE==π
∵S△BCE=BC2=,
∴阴影部分的面积为π﹣.
答案:π﹣.
12、我国古代数学的许多创新和发展都位居世界前列,如南宋数宁家杨辉(约13世纪)所著的《详解九章算术》一书中,用下图的三角形解释二项和的展开式的各项系数,此三角形称为“杨辉三角”.
①
①①
①②①
①③③①
①④⑥④①
①⑤⑩⑩⑤①
根据“杨辉三角”请计算的展开式中第三项的系数为
【提示】根据图形中的规律即可求出的展开式中第三项的系数.
【答案】190
【解析】找规律发现的第三项系数为;
的第三项系数为;
的第三项系数为;
不难发现的第三项系数为,
第三项系数为,
【说明】此题考查了通过观察、分析、归纳发现其中的规律,并应用发现的规律解决问题的能力.
二、选择题(本大题共有4 题,满分20 分,每题5 分)每题有且只有一个正确答案,考生应在答题纸的相应位置,将代表正确选项的小方格涂黑.
13、当时,、、、之间的大小关系是
A. B. C. D.
【提示】利用特殊值法进行计算即可解答.
【答案】C
【解析】,当时,,,,,,
,故选:.
【说明】本题考查了实数大小比较,算术平方根,熟练掌握特殊值法进行计算是解题的关键.
14、二十四节气,是我国古人根据地球在黄道(即地球绕太阳公转的轨道)上的位置变化而制定的,每一个节气分别相对应于地球在黄道上每运转所到达的一定位置,反映了太阳对地球产生的影响.它凝聚着中华文明的历史文化精华,在国际气象界,二十四节气被誉为“中国的第五大发明”.如图是地球绕太阳公转的轨道图,若将其近似看作圆形,其半径为,则从每年的立春到立夏,地球绕太阳公转的路程是
A. B. C. D.
【提示】可得从每年的立春到立夏地球绕太阳公转的圆心角度数为,根据扇形的弧长公式计算即可求解.
【答案】A;
【解答】解:从每年的立春到立夏地球绕太阳公转的圆心角度数为,
地球绕太阳公转的路程是.故选:.
【说明】本题考查了列代数式,关键是熟练掌握扇形的弧长公式.
15、为了了解三中九年级840名学生的体重情况,从中抽取100名学生的体重进行分析.在这项调查中,样本是指( )
A.840名学生
B.被抽取的100名学生
C.840名学生的体重
D.被抽取的100名学生的体重
【提示】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
【答案】D
【解答】样本是被抽取的100名学生的体重.故选:D.
【说明】考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
16、如图是一个无理数生成器的工作流程图,根据该流程图,下面说法:
①当输出值为时,输入值为3或9;
②当输入值为16时,输出值为;
③对于任意的正无理数,都存在正整数,使得输入后能够输出;
④存在这样的正整数,输入之后,该生成器能够一直运行,但始终不能输出值.其中错误的是
A.①② B.②④ C.①④ D.①③
【提示】根据运算规则即可求解.
【答案】D
【解答】:①的值不唯一.或或81等,故①说法错误;②输入值为16时,,,即,故②说法正确;③对于任意的正无理数,都存在正整数,使得输入后能够输出,如输入,故③说法错误;④当时,始终输不出值.因为1的算术平方根是1,一定是有理数,故④原说法正确.其中错误的是①③.故选:.
【说明】此题主要考查了无理数的定义,其中初中范围内学习的无理数有:,等;开方开不尽的数;以及像,等有这样规律的数.
三、解答题(本大题共有5题,满分14+14+14+16+18=76分,解答下列各题必须写出必要的步骤)
17. (本题满分14分)
(1)若分式的值是负整数,求:整数的值;
(2)设a>b>0,a2+b2﹣4ab=0,求值:;
【提示】(1)据分式的加法法则把原式变形,根据题意计算即可;
(2)原式利用完全平方公式变形,开方表示出a+b与b﹣a,代入原式计算即可求出值;
【解答】(1),由题意得,m﹣5=﹣1,
解得:m=4,故答案为:4.
(2)∵a>b>0,a2+b2﹣4ab=0,∴(a﹣b)2=2ab,(a+b)2=6ab,
∴a﹣b,a+b(负值舍去),则,故答案为:
【说明】本题考查了分式的值,熟练掌握运算法则是解本题的关键.
18. (本题满分14分)
如图,点A的坐标为,点B是x轴正半轴上的一点,
将线段AB绕点A按逆时针方向旋转60°得到线段AC;
若点C的坐标为,求m的值;
【提示】过C作CD⊥x轴于D,CE⊥y轴于E,
根据将线段AB绕点A按逆时针方向旋转60°得到线段AC,
可得△ABC是等边三角形,又A(0,2),C(m,3),即得,
可得,,从而,
即可解得.
【答案】
【解析】过C作CD⊥x轴于D,CE⊥y轴于E,如图所示:
∵CD⊥x轴,CE⊥y轴,∴∠CDO=∠CEO=∠DOE=90°,
∴四边形EODC是矩形,
∵将线段AB绕点A按逆时针方向旋转60°得到线段AC,
∴AB=AC,∠BAC=60°,∴△ABC是等边三角形,∴AB=AC=BC,
∵A(0,2),C(m,3),∴CE=m=OD,CD=3,OA=2,
∴AE=OE OA=CD OA=1,∴,
在Rt△BCD中,,
在Rt△AOB中,,
∵OB+BD=OD=m,∴,
化简变形得:3m4 22m2 25=0,解得:或(舍去),
∴,故C正确.故选:C.
【说明】本题考查直角坐标系中的旋转变换,解题的关键是熟练应用勾股定理,用含m的代数式表示相关线段的长度.
19. (本题满分14分)
如图,AB是⊙O的弦,AB=2,点C是⊙O上的一个动点,
且∠ACB=60°,若点M,N分别是AB,BC的中点,
求图中阴影部分面积的最大值;
【答案】
【解析】连接OA、OB、OM,如图,
∵∠ACB=60°,∴∠AOB=120°,
∵OA=OB,∴∠OAB=∠OBA=30°,
∵AM=BM=AB=,∴OM⊥AB,∴tan30°=,
∴OM=×=1,∴OA=2OM=2,
∵点M、N分别是AB、BC的中点,
∴MN∥AC,MN=AC,∴△MBN∽△ABC,
∴=()2=,
∴当△ABC的面积最大时,△MBN的面积最大,
∵C、O、M在一条直线时,△ABC的面积最大,
∴△ABC的面积最大值为:××(2+1)=3,
∴△MBN的面积最大值为:,
∵S弓形=S扇形OAB﹣S△AOB=﹣=﹣,
∴此时,S阴影=﹣+=﹣,
答案:﹣.
20. (本题满分16分)
如图,在△ABC中,BA=BC,D在边CB上,且DB=DA=AC.
(1)如图1,填空∠B= °,∠C= °;
(2)若M为线段BC上的点,过M作直线MH⊥AD于H,分别交直线AB、AC与点N、E,如图2
①求证:△ANE是等腰三角形;
②试写出线段BN、CE、CD之间的数量关系,并加以证明.
【解析】(1)∵BA=BC,∴∠BCA=∠BAC,
∵DA=DB,∴∠BAD=∠B,
∵AD=AC,∴∠ADC=∠C=∠BAC=2∠B,∴∠DAC=∠B,
∵∠DAC+∠ADC+∠C=180°,∴2∠B+2∠B+∠B=180°,
∴∠B=36°,∠C=2∠B=72°,
答案:36;72;
(2)①在△ADB中,∵DB=DA,∠B=36°,
∴∠BAD=36°,
在△ACD中,∵AD=AC,
∴∠ACD=∠ADC=72°,
∴∠CAD=36°,
∴∠BAD=∠CAD=36°,
∵MH⊥AD,
∴∠AHN=∠AHE=90°,
∴∠AEN=∠ANE=54°,
即△ANE是等腰三角形;
②CD=BN+CE.
证明:由①知AN=AE,
又∵BA=BC,DB=AC,
∴BN=AB﹣AN=BC﹣AE,CE=AE﹣AC=AE﹣BD,
∴BN+CE=BC﹣BD=CD,
即CD=BN+CE.
21. (本题满分18分)
观察以下等式:
第1个等式:(x﹣1)(x+1)=x2﹣1;
第2个等式:(x﹣1)(x2+x+1)=x3﹣1
第3个等式:(x﹣1)(x3+x2+x+1)=x4﹣1:…
按照以上规律,解决下列问题:
(1)写出第4个等式:(x﹣1)(x4+x3+x2+x+1)= ;
(2)写出你猜想的第n个等式:(x﹣1)(xn+xn﹣1+…+x+1)= ;
(3)请利用上述规律,确定22019+22018+…+2+1的个位数字是多少?
【分析】(1)仿照阅读材料中的等式写出第4个等式即可;
(2)归纳总结得到一般性规律,写出即可;
(3)利用得出的规律化简,计算即可求出值.
【答案】(1)x5﹣1;(2)xn+1﹣1;(3)5;
【解答】(1)(x﹣1)(x4+x3+x2+x+1)=x5﹣1;
(2)(x﹣1)(xn+xn﹣1+…+x+1)=xn+1﹣1;
(3)原式=(2﹣1)(22019+22018+…+2+1)=22020﹣1,
∵21=2,22=4,23=8,24=16,25=32,
∴2的个位数2,4,8,6循环,
∵2020=505×4,
∴22020的个位数为6,
则原式的个位数为5.
故答案为:(1)x5﹣1;(2)xn+1﹣1
【点评】此题考查了平方差公式,尾数特征,规律型:数字的变化类,以及多项式乘以多项式,熟练掌握运算法则是解本题的关键.
【沪教版2020】高中数学 新高一 摸底测试练习卷【3】
考生注意:
1.本试卷含三个大题,共21题.答题时,考生务必按答题要求在答题纸规定的位置上作答;
2.解答题必须写在试卷题号对应的区域相应位置,并写出解题的主要步骤;
一、填空题(本大题共12题,满分54分,第1~6题每题4分,第7~12题每题5分)考生应在答题纸相应编号的空格内直接填写结果.
1、计算: .
2、式子有意义的的取值范围是
3、设,,,则,,从小到大的顺序是
4、如图,数轴上,两点对应的数分别是和,对于以下四个式子:①;②;③:④,其中值为负数的是
5、如图,传送带的一个转动轮的半径为18cm,转动轮转n°,传送带上的物品A被传送12πcm,则n= .
6、图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空余的部分的面积是
7、随着某地公交票制票价调整,公交集团更换了新版公交站票,乘客在乘车时可以通过新版公交站牌计算乘车费用,新版站牌每一个站名上方都有一个相应的数字,将上下车站站名称对应数字相减取绝对值就是乘车路程,再按照其所在计价区段,参考票制规则计算票价,具体来说:
乘车路程计价区段
对应票价(元 2 3 4
另外,一卡通刷卡实行5折优惠,小明用一卡通乘车上车时站名上对应的数字是5,下车时站名上对应的数字
是22,那么小明乘车的费用是 元
8、某快餐店销售A、B两种快餐,每份利润分别为12元、8元,每天卖出份数分别为40份、80份.该店为了增加利润,准备降低每份A种快餐的利润,同时提高每份B种快餐的利润.售卖时发现,在一定范围内,每份A种快餐利润每降1元可多卖2份,每份B种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变,那么这两种快餐一天的总利润最多是 元.
9、小淇将展开后得到,小尧将展开后得到,若两人计算过程无误,则的值为
10、古希腊数学家把1,3,6,10,15,21,…这样的数叫做三角形数,因为它的规律性可以用如图表示.根据图形,若把第一个图形表示的三角形数记为a1=1,第二个图形表示的三角形数记为a2=3,…,则第n个图形表示的三角形数an= .(用含n的式子表达)
11、如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=2;
以点C为圆心,CB长为半径画弧,
分别交AC,AB于点D,E,
则图中阴影部分的面积为 (结果保留π).
12、我国古代数学的许多创新和发展都位居世界前列,如南宋数宁家杨辉(约13世纪)所著的《详解九章算术》一书中,用下图的三角形解释二项和的展开式的各项系数,此三角形称为“杨辉三角”.
①
①①
①②①
①③③①
①④⑥④①
①⑤⑩⑩⑤①
根据“杨辉三角”请计算的展开式中第三项的系数为
二、选择题(本大题共有4 题,满分20 分,每题5 分)每题有且只有一个正确答案,考生应在答题纸的相应位置,将代表正确选项的小方格涂黑.
13、当时,、、、之间的大小关系是
A. B. C. D.
14、二十四节气,是我国古人根据地球在黄道(即地球绕太阳公转的轨道)上的位置变化而制定的,每一个节气分别相对应于地球在黄道上每运转所到达的一定位置,反映了太阳对地球产生的影响.它凝聚着中华文明的历史文化精华,在国际气象界,二十四节气被誉为“中国的第五大发明”.如图是地球绕太阳公转的轨道图,若将其近似看作圆形,其半径为,则从每年的立春到立夏,地球绕太阳公转的路程是
A. B. C. D.
15、为了了解三中九年级840名学生的体重情况,从中抽取100名学生的体重进行分析.在这项调查中,样本是指( )
A.840名学生
B.被抽取的100名学生
C.840名学生的体重
D.被抽取的100名学生的体重
16、如图是一个无理数生成器的工作流程图,根据该流程图,下面说法:
①当输出值为时,输入值为3或9;
②当输入值为16时,输出值为;
③对于任意的正无理数,都存在正整数,使得输入后能够输出;
④存在这样的正整数,输入之后,该生成器能够一直运行,但始终不能输出值.其中错误的是
A.①② B.②④ C.①④ D.①③
三、解答题(本大题共有5题,满分14+14+14+16+18=76分,解答下列各题必须写出必要的步骤)
17. (本题满分14分)
(1)若分式的值是负整数,求:整数的值;
(2)设a>b>0,a2+b2﹣4ab=0,求值:;
18. (本题满分14分)
如图,点A的坐标为,点B是x轴正半轴上的一点,
将线段AB绕点A按逆时针方向旋转60°得到线段AC;
若点C的坐标为,求m的值;
19. (本题满分14分)
如图,AB是⊙O的弦,AB=2,点C是⊙O上的一个动点,
且∠ACB=60°,若点M,N分别是AB,BC的中点,
求图中阴影部分面积的最大值;
20. (本题满分16分)
如图,在△ABC中,BA=BC,D在边CB上,且DB=DA=AC.
(1)如图1,填空∠B= °,∠C= °;
(2)若M为线段BC上的点,过M作直线MH⊥AD于H,分别交直线AB、AC与点N、E,如图2
①求证:△ANE是等腰三角形;
②试写出线段BN、CE、CD之间的数量关系,并加以证明.
21. (本题满分18分)
观察以下等式:
第1个等式:(x﹣1)(x+1)=x2﹣1;
第2个等式:(x﹣1)(x2+x+1)=x3﹣1
第3个等式:(x﹣1)(x3+x2+x+1)=x4﹣1:…
按照以上规律,解决下列问题:
(1)写出第4个等式:(x﹣1)(x4+x3+x2+x+1)= ;
(2)写出你猜想的第n个等式:(x﹣1)(xn+xn﹣1+…+x+1)= ;
(3)请利用上述规律,确定22019+22018+…+2+1的个位数字是多少?
【教师版】
【沪教版2020】高中数学 新高一 摸底测试练习卷【3】
考生注意:
1.本试卷含三个大题,共21题.答题时,考生务必按答题要求在答题纸规定的位置上作答;
2.解答题必须写在试卷题号对应的区域相应位置,并写出解题的主要步骤;
一、填空题(本大题共12题,满分54分,第1~6题每题4分,第7~12题每题5分)考生应在答题纸相应编号的空格内直接填写结果.
1、计算: .
【提示】同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加.据此计算即可.
【答案】
【解析】,故答案为:.
【说明】本题考查了同底数幂的乘法,掌握幂的运算法则是解答本题的关键.
2、式子有意义的的取值范围是
【提示】根据分式有意义,二次根式有意义的条件进行判断即可;
【答案】x≥﹣1且x≠0;
【解析】由题意得,x+1≥0且x≠0,即x≥﹣1且x≠0,
【说明】本题考查二次根式、分式有意义的条件,掌握被开方数大于或等于0,分母不为0分别是二次根式和分式意义的条件是正确判断的前提;
3、设,,,则,,从小到大的顺序是
【提示】将c分母有理化再进行比较即可
【答案】 a<c<b
【解析】由
又由;
又∵a2=()2=7+2,c2=()2=5+2,且,∴a2<c2,
∴a<c,∴a<c<b.故答案为a<c<b.
【说明】本题考查了分母有理化,找到有理化因式是解题的关键.
4、如图,数轴上,两点对应的数分别是和,对于以下四个式子:①;②;③:④,其中值为负数的是
【提示】根据图示,可得,,据此逐项判断即可.
【答案】②④
【解析】根据图示,可得,,①;②;③;④.
故其中值为负数的是②④.
【说明】此题主要考查了绝对值的含义和求法,以及数轴的特征和应用,要熟练掌握,解答此题的关键是判断出、的取值范围;
5、如图,传送带的一个转动轮的半径为18cm,转动轮转n°,传送带上的物品A被传送12πcm,则n= .
【提示】数形结合地分析
【答案】120°
【解析】∵物品A被传送的距离等于转动了n°的弧长,∴=12π,
解得:n=120°,答案:120°.
【说明】熟悉弧长公式;
6、图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空余的部分的面积是
【提示】中间部分的四边形是正方形,表示出边长,则面积可以求得.
【答案】(a﹣b)2
【解析】中间部分的四边形是正方形,边长是a+b﹣2b=a﹣b,则面积是(a﹣b)2
【说明】本题考查了列代数式,正确表示出小正方形的边长是关键.
7、随着某地公交票制票价调整,公交集团更换了新版公交站票,乘客在乘车时可以通过新版公交站牌计算乘车费用,新版站牌每一个站名上方都有一个相应的数字,将上下车站站名称对应数字相减取绝对值就是乘车路程,再按照其所在计价区段,参考票制规则计算票价,具体来说:
乘车路程计价区段
对应票价(元 2 3 4
另外,一卡通刷卡实行5折优惠,小明用一卡通乘车上车时站名上对应的数字是5,下车时站名上对应的数字
是22,那么小明乘车的费用是 元
【提示】首先用下车时站名上对应的数字减去上车时站名上对应的数字,求出小明乘车的路程是多少,进而求出相应的票价是多少;然后用它乘以0.5,求出小明乘车的费用是多少元即可.
【答案】2
【解析】因为小明乘车的路程是:,所以小明乘车的费用是:(元;.
【说明】此题主要考查了有理数的混合运算,要熟练掌握有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算,解答此题的关键是求出小明乘车的路程、相应的票价是多少;
8、某快餐店销售A、B两种快餐,每份利润分别为12元、8元,每天卖出份数分别为40份、80份.该店为了增加利润,准备降低每份A种快餐的利润,同时提高每份B种快餐的利润.售卖时发现,在一定范围内,每份A种快餐利润每降1元可多卖2份,每份B种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变,那么这两种快餐一天的总利润最多是 元.
【提示】注意阅读理解转化;
【答案】1264
【解析】设每份A种快餐降价a元,则每天卖出(40+2a)份,每份B种快餐提高b元,
则每天卖出(80﹣2b)份,
由题意可得,40+2a+80﹣2b=40+80,解得a=b,
∴总利润W=(12﹣a)(40+2a)+(8+a)(80﹣2a)
=﹣4a2+48a+1120=﹣4(a﹣6)2+1264,
∵﹣4<0,∴当a=6时,W取得最大值1264,
即两种快餐一天的总利润最多为1264元.
答案:1264.
9、小淇将展开后得到,小尧将展开后得到,若两人计算过程无误,则的值为
【提示】根据完全平方公式展开求出,,根据平方差公式求值即可.
【答案】4043
【解答】解:展开后得到,,
展开后得到,,
.
【说明】本题考查了完全平方公式,平方差公式,掌握,是解题的关键.
10、古希腊数学家把1,3,6,10,15,21,…这样的数叫做三角形数,因为它的规律性可以用如图表示.根据图形,若把第一个图形表示的三角形数记为a1=1,第二个图形表示的三角形数记为a2=3,…,则第n个图形表示的三角形数an= .(用含n的式子表达)
【答案】
【解析】第1个图形表示的三角形数为1,
第2个图形表示的三角形数为1+2=3,
第3个图形表示的三角形数为1+2+3=6,
第4个图形表示的三角形数为1+2+3+4=10,
.....
第n个图形表示的三角形数为1+2+3+4+......+(n﹣1)+n=;
11、如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=2;
以点C为圆心,CB长为半径画弧,
分别交AC,AB于点D,E,
则图中阴影部分的面积为 (结果保留π).
【提示】注意图像的分割与拼接
【答案】
【解析】连接CE,
∵∠A=30°,
∴∠CBA=90°﹣∠A=60°,
∵CE=CB,
∴△CBE为等边三角形,
∴∠ECB=60°,BE=BC=2,
∴S扇形CBE==π
∵S△BCE=BC2=,
∴阴影部分的面积为π﹣.
答案:π﹣.
12、我国古代数学的许多创新和发展都位居世界前列,如南宋数宁家杨辉(约13世纪)所著的《详解九章算术》一书中,用下图的三角形解释二项和的展开式的各项系数,此三角形称为“杨辉三角”.
①
①①
①②①
①③③①
①④⑥④①
①⑤⑩⑩⑤①
根据“杨辉三角”请计算的展开式中第三项的系数为
【提示】根据图形中的规律即可求出的展开式中第三项的系数.
【答案】190
【解析】找规律发现的第三项系数为;
的第三项系数为;
的第三项系数为;
不难发现的第三项系数为,
第三项系数为,
【说明】此题考查了通过观察、分析、归纳发现其中的规律,并应用发现的规律解决问题的能力.
二、选择题(本大题共有4 题,满分20 分,每题5 分)每题有且只有一个正确答案,考生应在答题纸的相应位置,将代表正确选项的小方格涂黑.
13、当时,、、、之间的大小关系是
A. B. C. D.
【提示】利用特殊值法进行计算即可解答.
【答案】C
【解析】,当时,,,,,,
,故选:.
【说明】本题考查了实数大小比较,算术平方根,熟练掌握特殊值法进行计算是解题的关键.
14、二十四节气,是我国古人根据地球在黄道(即地球绕太阳公转的轨道)上的位置变化而制定的,每一个节气分别相对应于地球在黄道上每运转所到达的一定位置,反映了太阳对地球产生的影响.它凝聚着中华文明的历史文化精华,在国际气象界,二十四节气被誉为“中国的第五大发明”.如图是地球绕太阳公转的轨道图,若将其近似看作圆形,其半径为,则从每年的立春到立夏,地球绕太阳公转的路程是
A. B. C. D.
【提示】可得从每年的立春到立夏地球绕太阳公转的圆心角度数为,根据扇形的弧长公式计算即可求解.
【答案】A;
【解答】解:从每年的立春到立夏地球绕太阳公转的圆心角度数为,
地球绕太阳公转的路程是.故选:.
【说明】本题考查了列代数式,关键是熟练掌握扇形的弧长公式.
15、为了了解三中九年级840名学生的体重情况,从中抽取100名学生的体重进行分析.在这项调查中,样本是指( )
A.840名学生
B.被抽取的100名学生
C.840名学生的体重
D.被抽取的100名学生的体重
【提示】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
【答案】D
【解答】样本是被抽取的100名学生的体重.故选:D.
【说明】考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
16、如图是一个无理数生成器的工作流程图,根据该流程图,下面说法:
①当输出值为时,输入值为3或9;
②当输入值为16时,输出值为;
③对于任意的正无理数,都存在正整数,使得输入后能够输出;
④存在这样的正整数,输入之后,该生成器能够一直运行,但始终不能输出值.其中错误的是
A.①② B.②④ C.①④ D.①③
【提示】根据运算规则即可求解.
【答案】D
【解答】:①的值不唯一.或或81等,故①说法错误;②输入值为16时,,,即,故②说法正确;③对于任意的正无理数,都存在正整数,使得输入后能够输出,如输入,故③说法错误;④当时,始终输不出值.因为1的算术平方根是1,一定是有理数,故④原说法正确.其中错误的是①③.故选:.
【说明】此题主要考查了无理数的定义,其中初中范围内学习的无理数有:,等;开方开不尽的数;以及像,等有这样规律的数.
三、解答题(本大题共有5题,满分14+14+14+16+18=76分,解答下列各题必须写出必要的步骤)
17. (本题满分14分)
(1)若分式的值是负整数,求:整数的值;
(2)设a>b>0,a2+b2﹣4ab=0,求值:;
【提示】(1)据分式的加法法则把原式变形,根据题意计算即可;
(2)原式利用完全平方公式变形,开方表示出a+b与b﹣a,代入原式计算即可求出值;
【解答】(1),由题意得,m﹣5=﹣1,
解得:m=4,故答案为:4.
(2)∵a>b>0,a2+b2﹣4ab=0,∴(a﹣b)2=2ab,(a+b)2=6ab,
∴a﹣b,a+b(负值舍去),则,故答案为:
【说明】本题考查了分式的值,熟练掌握运算法则是解本题的关键.
18. (本题满分14分)
如图,点A的坐标为,点B是x轴正半轴上的一点,
将线段AB绕点A按逆时针方向旋转60°得到线段AC;
若点C的坐标为,求m的值;
【提示】过C作CD⊥x轴于D,CE⊥y轴于E,
根据将线段AB绕点A按逆时针方向旋转60°得到线段AC,
可得△ABC是等边三角形,又A(0,2),C(m,3),即得,
可得,,从而,
即可解得.
【答案】
【解析】过C作CD⊥x轴于D,CE⊥y轴于E,如图所示:
∵CD⊥x轴,CE⊥y轴,∴∠CDO=∠CEO=∠DOE=90°,
∴四边形EODC是矩形,
∵将线段AB绕点A按逆时针方向旋转60°得到线段AC,
∴AB=AC,∠BAC=60°,∴△ABC是等边三角形,∴AB=AC=BC,
∵A(0,2),C(m,3),∴CE=m=OD,CD=3,OA=2,
∴AE=OE OA=CD OA=1,∴,
在Rt△BCD中,,
在Rt△AOB中,,
∵OB+BD=OD=m,∴,
化简变形得:3m4 22m2 25=0,解得:或(舍去),
∴,故C正确.故选:C.
【说明】本题考查直角坐标系中的旋转变换,解题的关键是熟练应用勾股定理,用含m的代数式表示相关线段的长度.
19. (本题满分14分)
如图,AB是⊙O的弦,AB=2,点C是⊙O上的一个动点,
且∠ACB=60°,若点M,N分别是AB,BC的中点,
求图中阴影部分面积的最大值;
【答案】
【解析】连接OA、OB、OM,如图,
∵∠ACB=60°,∴∠AOB=120°,
∵OA=OB,∴∠OAB=∠OBA=30°,
∵AM=BM=AB=,∴OM⊥AB,∴tan30°=,
∴OM=×=1,∴OA=2OM=2,
∵点M、N分别是AB、BC的中点,
∴MN∥AC,MN=AC,∴△MBN∽△ABC,
∴=()2=,
∴当△ABC的面积最大时,△MBN的面积最大,
∵C、O、M在一条直线时,△ABC的面积最大,
∴△ABC的面积最大值为:××(2+1)=3,
∴△MBN的面积最大值为:,
∵S弓形=S扇形OAB﹣S△AOB=﹣=﹣,
∴此时,S阴影=﹣+=﹣,
答案:﹣.
20. (本题满分16分)
如图,在△ABC中,BA=BC,D在边CB上,且DB=DA=AC.
(1)如图1,填空∠B= °,∠C= °;
(2)若M为线段BC上的点,过M作直线MH⊥AD于H,分别交直线AB、AC与点N、E,如图2
①求证:△ANE是等腰三角形;
②试写出线段BN、CE、CD之间的数量关系,并加以证明.
【解析】(1)∵BA=BC,∴∠BCA=∠BAC,
∵DA=DB,∴∠BAD=∠B,
∵AD=AC,∴∠ADC=∠C=∠BAC=2∠B,∴∠DAC=∠B,
∵∠DAC+∠ADC+∠C=180°,∴2∠B+2∠B+∠B=180°,
∴∠B=36°,∠C=2∠B=72°,
答案:36;72;
(2)①在△ADB中,∵DB=DA,∠B=36°,
∴∠BAD=36°,
在△ACD中,∵AD=AC,
∴∠ACD=∠ADC=72°,
∴∠CAD=36°,
∴∠BAD=∠CAD=36°,
∵MH⊥AD,
∴∠AHN=∠AHE=90°,
∴∠AEN=∠ANE=54°,
即△ANE是等腰三角形;
②CD=BN+CE.
证明:由①知AN=AE,
又∵BA=BC,DB=AC,
∴BN=AB﹣AN=BC﹣AE,CE=AE﹣AC=AE﹣BD,
∴BN+CE=BC﹣BD=CD,
即CD=BN+CE.
21. (本题满分18分)
观察以下等式:
第1个等式:(x﹣1)(x+1)=x2﹣1;
第2个等式:(x﹣1)(x2+x+1)=x3﹣1
第3个等式:(x﹣1)(x3+x2+x+1)=x4﹣1:…
按照以上规律,解决下列问题:
(1)写出第4个等式:(x﹣1)(x4+x3+x2+x+1)= ;
(2)写出你猜想的第n个等式:(x﹣1)(xn+xn﹣1+…+x+1)= ;
(3)请利用上述规律,确定22019+22018+…+2+1的个位数字是多少?
【分析】(1)仿照阅读材料中的等式写出第4个等式即可;
(2)归纳总结得到一般性规律,写出即可;
(3)利用得出的规律化简,计算即可求出值.
【答案】(1)x5﹣1;(2)xn+1﹣1;(3)5;
【解答】(1)(x﹣1)(x4+x3+x2+x+1)=x5﹣1;
(2)(x﹣1)(xn+xn﹣1+…+x+1)=xn+1﹣1;
(3)原式=(2﹣1)(22019+22018+…+2+1)=22020﹣1,
∵21=2,22=4,23=8,24=16,25=32,
∴2的个位数2,4,8,6循环,
∵2020=505×4,
∴22020的个位数为6,
则原式的个位数为5.
故答案为:(1)x5﹣1;(2)xn+1﹣1
【点评】此题考查了平方差公式,尾数特征,规律型:数字的变化类,以及多项式乘以多项式,熟练掌握运算法则是解本题的关键.
同课章节目录
