1.2.3 相反数 课件(共26张PPT)
文档属性
| 名称 | 1.2.3 相反数 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
七上数学同步精品课件
人教版七年级上册
1.2.3 相反数
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
第一章 有理数
1.借助数轴理解相反数的概念,并能求给定数的相反数;(重点)
2.了解一对相反数在数轴上的位置关系;(重点)
3.掌握双重符号的化简;(难点)
4.通过从数和形两个方面理解相反数,初步体会数形结合的思想方法.
有理数王国的公民“1”,有一天不小心掉进了一个魔瓶里. 谁知出来后竟变成胖乎乎的“0”,你说怪不怪?冷眼旁观的“2”说:“谁叫这瓶里睡着他的相反数兄弟呢?幸好我兄弟不在里面!”同学们,你想知道“1”的相反数兄弟是谁吗?为什么他俩见面后就变成“0”呢?就让我们一起走进神奇的相反数的世界吧!
0
1
动手操作——体验数学活动充满探索
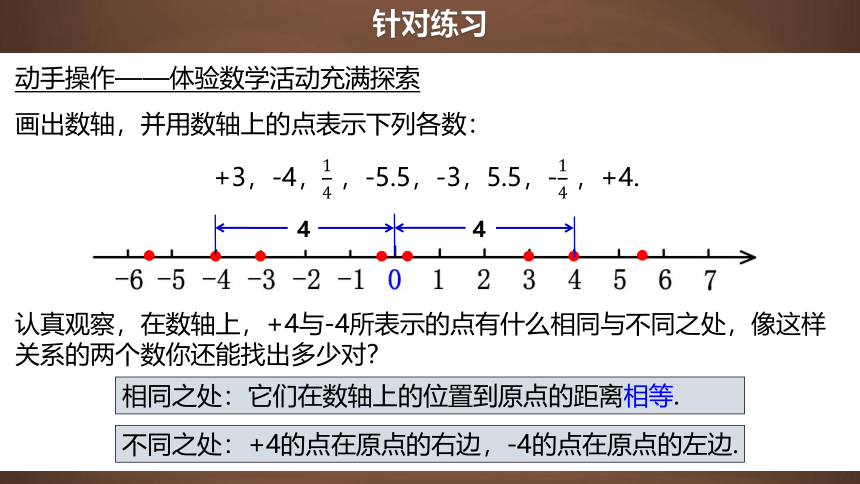
画出数轴,并用数轴上的点表示下列各数:
+3,-4, ,-5.5,-3,5.5,- ,+4.
4
4
认真观察,在数轴上,+4与-4所表示的点有什么相同与不同之处,像这样关系的两个数你还能找出多少对?
相同之处:它们在数轴上的位置到原点的距离相等.
不同之处:+4的点在原点的右边,-4的点在原点的左边.
数轴上与原点的距离是2的点有___个,这些点表示的数是______;与原点的距离是5的点有___个,这些点表示的数是______.
2
2和-2
2
5和-5
设a是一个正数,数轴上与原点的距离等于a的点有几个?这些点表示的数有什么关系?
2
5
2
5
像2和-2,5和-5这样,只有符号不同的两个数叫做互为相反数.
一般地,设a是一个正数,数轴上与原点距离是a的点有两个,它们分别在原点左右,表示-a和a. 我们说这两点关于原点对称.
这就是说,2的相反数是-2,-2的相反数是2;5的相反数是-5,-5的相反数是5.
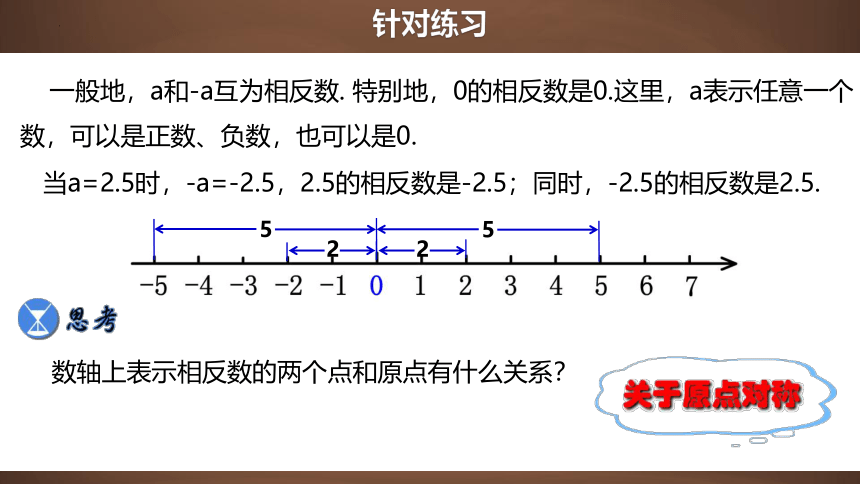
一般地,a和-a互为相反数. 特别地,0的相反数是0.这里,a表示任意一个数,可以是正数、负数,也可以是0.
当a=2.5时,-a=-2.5,2.5的相反数是-2.5;同时,-2.5的相反数是2.5.
2
5
2
5
数轴上表示相反数的两个点和原点有什么关系?
1.判断下列说法是否正确:
(1)-3是相反数; ( ) (2)+3是相反数; ( )
(3)3是-3的相反数;( ) (4)-3与+3互为相反数.( )
2.写出下列各数的相反数:
6,-8,-3.9, ,-,100,0.
解:相反数依次是-6,8,3.9,- ,,-100,0.
3.如果a=-a,那么表示a的点在数轴上的什么位置?______.
原点
结合数轴思考:
0的相反数是_____.
一个正数的相反数是一个 .
一个负数的相反数是一个 .
负数
正数
一个数的相反数是它本身的数是______.
0
0
例1.如图,四个有理数在数轴上的对应点分别为M,P,N,Q.若P到N的距离小于P到M的距离,且点M,N表示的有理数互为相反数,则图中的点表示正数的有( )
A.0个 B.1个 C.2个 D.3个
解:由M、N互为相反数,可确定原点O的位置如图所示.
由数轴知,图中表示正数的点有3个,是P,N,Q.
0
D
1.如图,数轴上的单位长度为1,有三个点A、B、C,若点A、C表示的数互为相反数,则图中点B对应的数是( )
A.-1 B.0 C.1 D.3
C
2.在数轴上,点A,B在原点O的同侧,分别表示数a,3,将点向左平移5个单位长度得到点C,若点C与点B所表示的数互为相反数,则a的值为( )
A.2 B.3 C.-1 D.0
A
1.设a表示一个数,-a一定是负数吗?
在这个数前加一个“-”号.
2.如何求一个数的相反数?
容易看出,在正数前面添上“-”号,就得到这个正数的相反数. 在任意一个数前面添上“-”号,新的数就是表示原数的相反数. 例如,-(+5)=___,-(-5)=___,-0=___.
-5
5
0
你能借助数轴说明-(-5)=+5吗?
-5和+5关于原点对称,它们互为相反数.
-(+1.1)表示什么?-(-7)呢?-(-9.8)呢?它们的结果应是多少?
由内向外依次去思考
【点睛】化简多重符号时,只需数一下数字前面有多少个负号,若有偶数个,则结果为正;若有奇数个,则结果为负;凡是“+”都去掉.
例2.化简下列各数:
(1) ;(2) ;(3) ;(4) ;
(5) ;(6) .
解:(1) ;(2) ;(3) ;
(4) ;(5) ;(6) .
化简下列各数:
(1) ; (2) ; (3) ;
(4) ; (5) ; (6) .
解:(1) ;(2) ;
(3) ;(4) ;
(5) ;(6) .
1.填空:(1)-5.8是______的相反数,_____的相反数是-(+4),b的相反数是____,0的相反数是_____.
(2)正数的相反数是_____,负数的相反数是______,_______的相反数是本身.
2.下列判断不正确的有( )
①互为相反数的两个数一定不相等;②互为相反数的数在数轴.上的点一定在原点的两边;③所有的有理数都有相反数;④相反数是符号相反的两个数.
A. 1个 B. 2个 C.3个 D. 4个
5.8
4
-b
0
负数
正数
0
C
3.下列各组数中,互为相反数的是( ).
A.+(-2)和-(+2) B.-(-2)和+(+2) C.-2和-(-2) D.-2和-(+2)
C
4.下列各对数中,互为相反数的有( )
①-1与+1;②+(+1)与-1;③-(-2)与+(-2);④-(-)与+(+) ;
⑤+[-(+1)]与-[+(-1)];⑥-(+2)与-(-2).
A.6对 B.5对 C.4对 D.3对
B
5.数轴上,若A,B表示互为相反数的两个数且A在B的右侧,并且这两点的距离为10,则点B表示的数是______.
-5
6.如图,在单位长度是1的数轴上,点A和点C所表示的两个数互为相反数,则点B表示的数是______.
﹣2
7.如图,数轴的单位长度为1,点A,B表示的数互为相反数,若数轴上有一点C到点B的距离为8个单位,则点C表示的数是__________.
11或-5
8.用“ ”与“ ”表示一种法则:(a b)=﹣b,(a b)=﹣a,如(2 3)=﹣3,则(2017 2018) (2016 2015)=__________.
2018
9.数轴上有A,B,C三点.点A,B表示的数互为相反数,且点A在点B的左边,同时点A,B相距8个单位;点A,C相距2个单位.点A,B,C表示的数各是多少?
解:因为点A、B表示的数互为相反数,且点A在点B的左边;
所以A为负数,B为正数;
因为点A、B相距8个单位长度;
所以点A表示的数为-4,点B表示的数为4;
因为点A、C相距2个单位长度;
所以点C表示的数为-6或-2;
所以点A表示的数为-4,点B表示的数为4,点C表示的数为-6或-2.如图所示:
10.化简下列各式,并解答问题:
①-(-2);②+(-);③-[-(-4)];④-[-(+3.5)];
⑤-{-[-(-5)]};⑥-{-[-(+5)]}.
问:(1)当+5前面有2 018个负号时,化简后结果是多少?
(2)当-5前面有2 019个负号时,化简后的结果是多少?你能总结出什么规律?
解:①-(-2)=2;②+(-=-;③-[-(-4)]=-4;
④-[-(+3.5)]=3.5;⑤-{-[-(-5)]}=5;⑥-{-[-(+5)]}=-5.
(1)当+5前面有2 018个负号时,化简后的结果是+5.
(2)当-5前面有2 019个负号时,化简后的结果是+5.
总结规律:一个数的前面有奇数个负号,化简后的结果等于它的相反数,有偶数个负号,化简后的结果等于它本身.
位置特征:1.分居原点左右;2.到原点距离相等.
a的相反数是-a ; 0的相反数是0
2
5
2
5
像2和-2,5和-5这样,只有符号不同的两个数叫做互为相反数.
一般地,设a是一个正数,数轴上与原点距离是a的点有两个,它们分别在原点左右,表示-a和a. 我们说这两点关于原点对称.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
七上数学同步精品课件
人教版七年级上册
1.2.3 相反数
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
第一章 有理数
1.借助数轴理解相反数的概念,并能求给定数的相反数;(重点)
2.了解一对相反数在数轴上的位置关系;(重点)
3.掌握双重符号的化简;(难点)
4.通过从数和形两个方面理解相反数,初步体会数形结合的思想方法.
有理数王国的公民“1”,有一天不小心掉进了一个魔瓶里. 谁知出来后竟变成胖乎乎的“0”,你说怪不怪?冷眼旁观的“2”说:“谁叫这瓶里睡着他的相反数兄弟呢?幸好我兄弟不在里面!”同学们,你想知道“1”的相反数兄弟是谁吗?为什么他俩见面后就变成“0”呢?就让我们一起走进神奇的相反数的世界吧!
0
1
动手操作——体验数学活动充满探索
画出数轴,并用数轴上的点表示下列各数:
+3,-4, ,-5.5,-3,5.5,- ,+4.
4
4
认真观察,在数轴上,+4与-4所表示的点有什么相同与不同之处,像这样关系的两个数你还能找出多少对?
相同之处:它们在数轴上的位置到原点的距离相等.
不同之处:+4的点在原点的右边,-4的点在原点的左边.
数轴上与原点的距离是2的点有___个,这些点表示的数是______;与原点的距离是5的点有___个,这些点表示的数是______.
2
2和-2
2
5和-5
设a是一个正数,数轴上与原点的距离等于a的点有几个?这些点表示的数有什么关系?
2
5
2
5
像2和-2,5和-5这样,只有符号不同的两个数叫做互为相反数.
一般地,设a是一个正数,数轴上与原点距离是a的点有两个,它们分别在原点左右,表示-a和a. 我们说这两点关于原点对称.
这就是说,2的相反数是-2,-2的相反数是2;5的相反数是-5,-5的相反数是5.
一般地,a和-a互为相反数. 特别地,0的相反数是0.这里,a表示任意一个数,可以是正数、负数,也可以是0.
当a=2.5时,-a=-2.5,2.5的相反数是-2.5;同时,-2.5的相反数是2.5.
2
5
2
5
数轴上表示相反数的两个点和原点有什么关系?
1.判断下列说法是否正确:
(1)-3是相反数; ( ) (2)+3是相反数; ( )
(3)3是-3的相反数;( ) (4)-3与+3互为相反数.( )
2.写出下列各数的相反数:
6,-8,-3.9, ,-,100,0.
解:相反数依次是-6,8,3.9,- ,,-100,0.
3.如果a=-a,那么表示a的点在数轴上的什么位置?______.
原点
结合数轴思考:
0的相反数是_____.
一个正数的相反数是一个 .
一个负数的相反数是一个 .
负数
正数
一个数的相反数是它本身的数是______.
0
0
例1.如图,四个有理数在数轴上的对应点分别为M,P,N,Q.若P到N的距离小于P到M的距离,且点M,N表示的有理数互为相反数,则图中的点表示正数的有( )
A.0个 B.1个 C.2个 D.3个
解:由M、N互为相反数,可确定原点O的位置如图所示.
由数轴知,图中表示正数的点有3个,是P,N,Q.
0
D
1.如图,数轴上的单位长度为1,有三个点A、B、C,若点A、C表示的数互为相反数,则图中点B对应的数是( )
A.-1 B.0 C.1 D.3
C
2.在数轴上,点A,B在原点O的同侧,分别表示数a,3,将点向左平移5个单位长度得到点C,若点C与点B所表示的数互为相反数,则a的值为( )
A.2 B.3 C.-1 D.0
A
1.设a表示一个数,-a一定是负数吗?
在这个数前加一个“-”号.
2.如何求一个数的相反数?
容易看出,在正数前面添上“-”号,就得到这个正数的相反数. 在任意一个数前面添上“-”号,新的数就是表示原数的相反数. 例如,-(+5)=___,-(-5)=___,-0=___.
-5
5
0
你能借助数轴说明-(-5)=+5吗?
-5和+5关于原点对称,它们互为相反数.
-(+1.1)表示什么?-(-7)呢?-(-9.8)呢?它们的结果应是多少?
由内向外依次去思考
【点睛】化简多重符号时,只需数一下数字前面有多少个负号,若有偶数个,则结果为正;若有奇数个,则结果为负;凡是“+”都去掉.
例2.化简下列各数:
(1) ;(2) ;(3) ;(4) ;
(5) ;(6) .
解:(1) ;(2) ;(3) ;
(4) ;(5) ;(6) .
化简下列各数:
(1) ; (2) ; (3) ;
(4) ; (5) ; (6) .
解:(1) ;(2) ;
(3) ;(4) ;
(5) ;(6) .
1.填空:(1)-5.8是______的相反数,_____的相反数是-(+4),b的相反数是____,0的相反数是_____.
(2)正数的相反数是_____,负数的相反数是______,_______的相反数是本身.
2.下列判断不正确的有( )
①互为相反数的两个数一定不相等;②互为相反数的数在数轴.上的点一定在原点的两边;③所有的有理数都有相反数;④相反数是符号相反的两个数.
A. 1个 B. 2个 C.3个 D. 4个
5.8
4
-b
0
负数
正数
0
C
3.下列各组数中,互为相反数的是( ).
A.+(-2)和-(+2) B.-(-2)和+(+2) C.-2和-(-2) D.-2和-(+2)
C
4.下列各对数中,互为相反数的有( )
①-1与+1;②+(+1)与-1;③-(-2)与+(-2);④-(-)与+(+) ;
⑤+[-(+1)]与-[+(-1)];⑥-(+2)与-(-2).
A.6对 B.5对 C.4对 D.3对
B
5.数轴上,若A,B表示互为相反数的两个数且A在B的右侧,并且这两点的距离为10,则点B表示的数是______.
-5
6.如图,在单位长度是1的数轴上,点A和点C所表示的两个数互为相反数,则点B表示的数是______.
﹣2
7.如图,数轴的单位长度为1,点A,B表示的数互为相反数,若数轴上有一点C到点B的距离为8个单位,则点C表示的数是__________.
11或-5
8.用“ ”与“ ”表示一种法则:(a b)=﹣b,(a b)=﹣a,如(2 3)=﹣3,则(2017 2018) (2016 2015)=__________.
2018
9.数轴上有A,B,C三点.点A,B表示的数互为相反数,且点A在点B的左边,同时点A,B相距8个单位;点A,C相距2个单位.点A,B,C表示的数各是多少?
解:因为点A、B表示的数互为相反数,且点A在点B的左边;
所以A为负数,B为正数;
因为点A、B相距8个单位长度;
所以点A表示的数为-4,点B表示的数为4;
因为点A、C相距2个单位长度;
所以点C表示的数为-6或-2;
所以点A表示的数为-4,点B表示的数为4,点C表示的数为-6或-2.如图所示:
10.化简下列各式,并解答问题:
①-(-2);②+(-);③-[-(-4)];④-[-(+3.5)];
⑤-{-[-(-5)]};⑥-{-[-(+5)]}.
问:(1)当+5前面有2 018个负号时,化简后结果是多少?
(2)当-5前面有2 019个负号时,化简后的结果是多少?你能总结出什么规律?
解:①-(-2)=2;②+(-=-;③-[-(-4)]=-4;
④-[-(+3.5)]=3.5;⑤-{-[-(-5)]}=5;⑥-{-[-(+5)]}=-5.
(1)当+5前面有2 018个负号时,化简后的结果是+5.
(2)当-5前面有2 019个负号时,化简后的结果是+5.
总结规律:一个数的前面有奇数个负号,化简后的结果等于它的相反数,有偶数个负号,化简后的结果等于它本身.
位置特征:1.分居原点左右;2.到原点距离相等.
a的相反数是-a ; 0的相反数是0
2
5
2
5
像2和-2,5和-5这样,只有符号不同的两个数叫做互为相反数.
一般地,设a是一个正数,数轴上与原点距离是a的点有两个,它们分别在原点左右,表示-a和a. 我们说这两点关于原点对称.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
