1.2.5 有理数大小的比较 课件(共27张PPT)
文档属性
| 名称 | 1.2.5 有理数大小的比较 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 10:13:16 | ||
图片预览







文档简介
(共27张PPT)
七上数学同步精品课件
人教版七年级上册
1.2.5 有理数大小的比较
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
第一章 有理数
1.掌握有理数大小的比较法则;(重点)
2.会比较有理数的大小,并能正确地使用“>”或“<”号连接; (重点)
3.能初步进行有理数大小比较的推理和书写.(难点)
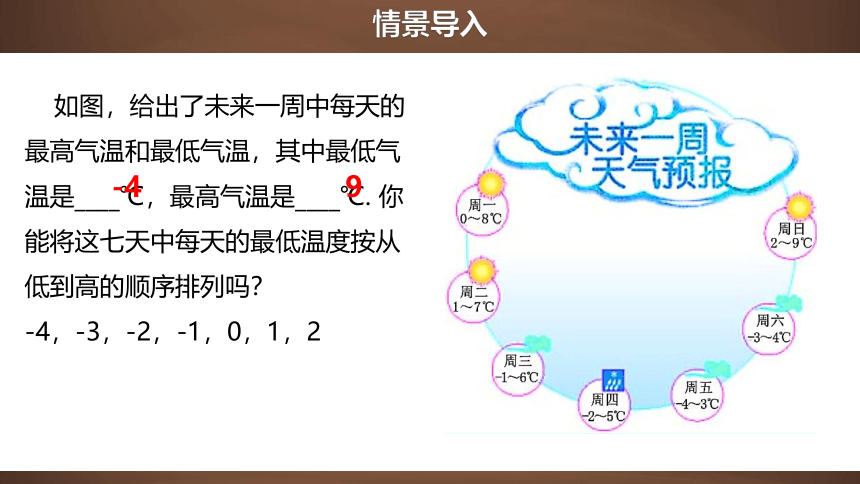
如图,给出了未来一周中每天的最高气温和最低气温,其中最低气温是____℃,最高气温是____℃. 你能将这七天中每天的最低温度按从低到高的顺序排列吗?
-4,-3,-2,-1,0,1,2
-4
9
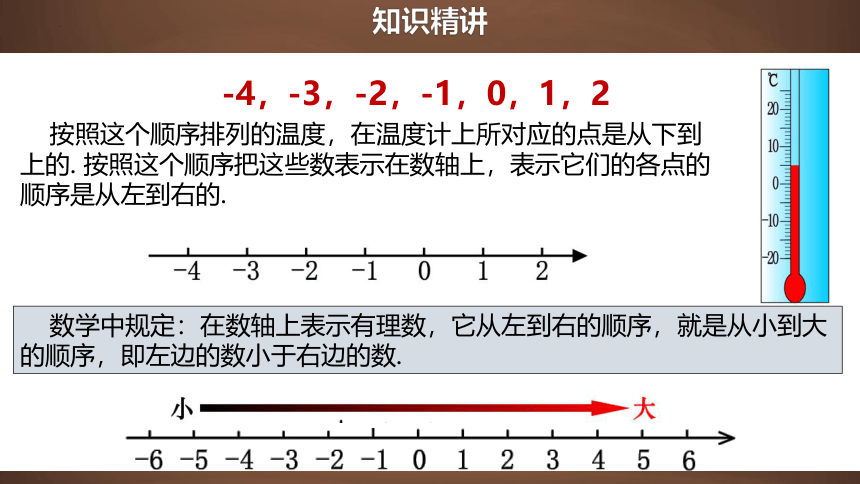
按照这个顺序排列的温度,在温度计上所对应的点是从下到上的. 按照这个顺序把这些数表示在数轴上,表示它们的各点的顺序是从左到右的.
-4,-3,-2,-1,0,1,2
数学中规定:在数轴上表示有理数,它从左到右的顺序,就是从小到大的顺序,即左边的数小于右边的数.
有理数大小的比较方法1---数轴比较法
在数轴上表示的两个数,右边的数总比左边的数大.
有没有最大的有理数 有没有最小的有理数 为什么
知识精讲
借助数轴比较有理数的大小
例1.在数轴上表示数-3,-4,-,2.5,0,并比较它们的大小,将它们按从小到大的顺序用“<”号连接.
解:
-3,-5,4,0在数轴上表示如图:
将它们按从小到大的顺序排列为:
-4 <-3 <-<0 <2.5
-5 -4 -3 -2 -1 0 1 2 3 4 5
●
●
●
●
●
-
2.5
因为在数轴上表示的两个数,右边的数总比左边的数大.
在数轴上表示下列各数:0,-3.5,-(-4),,-2.5,+5,并用“<”号连接.
解:
0,-3.5,-(-4),,-2.5,+5在数轴上表示如图:
化简:-(-4)=4,=
-
●
●
●
●
●
●
-
将它们按从小到大的顺序排列为:-3.5<-2.5<0<<-(-4)<+5.
1.对于正数、0、负数这三类数,它们之间有什么大小关系?
一般地,正数大于0,0大于负数,正数大于负数;
例如:1____0,0____-1,1____-1.
>
>
>
2.两个负数之间如何比较大小?
两个负数,绝对值大的反而小.
-3和-6如何比较大小呢?
有理数大小的比较方法2---数的相对大小比较法
一般地,正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
例2.比较下列各对数的大小.
(1) -(-1)和-(+2);(2)-和-;(3) -(-0.3)和|-|.
解:(1)先化简,-(-1)=1,-(+2)=-2
因为正数大于负数,
所以1>-2,即 -(-1)>-(+2)
(2)这是两个负数比较大小,先求它们的绝对值.
|-|= ,|-|= =
因为< ,即|-|<|-|,
所以->-
(3)先化简,-(-0.3)=0.3,|-|=
0.3< ,即-(-0.3)<|-|.
【点睛】异号两数比较大小,要考虑它们的正负;同号两数比较大小,要考虑它们的绝对值.
典例解析
比较两个负数大小的方法步骤是:
(1)如果需要化简,要先进行化简;
(2)再分别求出两个负数的绝对值;
(3)比较两个绝对值的大小;
(4)根据“两个负数,绝对值大的反而小”做出正确的判断.
比较下列各对数的大小:
(1)3和-5 (2) -3和-5 (3)-2.5和-|-2.25| (4)-和-
解:(1)因为正数大于负数,所以3>-5;
(2)因为|-3|<|-5|,所以-3>-5
(3)先化简,-|-2.25|=-2.25,因为|-2.5|>|-2.25|,
所以 -2.5<-|-2.25|
(4) |-|==,|-|==,因为>,所以->- .
例3.某公司抽检盒装牛奶的容量,超过标准容量的部分记为正数,不足的部分记为负数.从容量的角度看,以下四盒牛奶容量最接近标准的是( )
A. B. C. D.
【分析】解:A.+0.8的绝对值是0.8;B.-1.2的绝对值是1.2;C.-0.5的绝对值是0.5;D.+1的绝对值是1.
因为0.5<0.8<1<1.2,所以C选项的绝对值最小.
C
2020年末“霸王级”寒潮来袭,全国各地气温骤降,如图表示2021年元月某天山西省四个城市的天气情况.这一天最高气温最低的城市为( )
A.大同 B.太原 C.长治 D.晋城
A
例4.如果 ,试比较 的大小.
解:因为
所以
因为 ,
所以 ,
所以 , ,
所以 .
0
a
b
-b
-a
1.如图,点A表示的有理数是x,则x,-x,1的大小关系为( )
A.-x<x<1 B. x<-x<1 C. x<1<-x D. 1<-x<x
B
2.若0<x<1,则m、-m、的大小关系是( )
A.m<-m< B. -m<m< C. <m<-m D. <-m<
B
1.下列说法中正确的是( )
A.两个负数中,绝对值大的数就大 B.两个数中,绝对值较小的数就小
C.0没有绝对值 D.绝对值相等的两个数不一定相等
2.下列四组有理数大小的比较正确的是( )
A.-> B.->- C.->- D.>
D
D
3.若有理数a,b在数轴.上对应点的位置如图所示,则下列正确的是( )
A.|b|>-a B. |a|>-b C. b>a D. |a|>|b|
A
4.下列判断,正确的是( )
A.若a>b,则│a│>│b│ B.若│a│>│b│,则a>b
C.若a<b<0,则│a│<│b│ D.若a>b>0,则│a│>│b│
D
如a=1,b=-2
如a=-3,b=2
如a=-3,b=-2
5.绝对值大于1而不大于4的整数有__________________________.
-4、-3、-2、2、3、4
乙
6.厂家检测甲、乙、丙、丁四个足球的质量,超过标准质量的克数记为正数,不足标准质量的克数记为负数,结果如图所示,其中最接近标准质量的足球是______.
7.问题:比较-与+(-)的大小.
解:化简可得-=,+(-)=- ①.
因为=,=②
又==③
所以<-,④
所以-<+(-) ⑤.
本题是从______开始出现错误的(填序号).请给出正确的解题过程.
8.写出符合下列条件的数:
(1)大于﹣3且小于2的所有整数;
(2)绝对值大于2且小于5的所有负整数;
(3)在数轴上,与表示﹣1的点的距离为2的数.
解:(1)由题意得,大于﹣3且小于2的所有整数有﹣2、﹣1、0、1;
(2)根据题意得,绝对值大于2且小于5的所有负整数有:﹣3、﹣4;
(3)设在数轴上,与表示﹣1的点的距离为2的数为x,
则有:|x﹣(﹣1)|=2,
解得:x=1,或x=﹣3.
∴在数轴上,与表示﹣1的点的距离为2的所有数为1,﹣3.
9.若|a|=-a,|b|=b,|c|=-c,|d|=-d,a,b,c,d都不为零,并且|a|>|b|>|c|>|d|,请把a,b,c,d四个数从小到大用“<”号连结.
【分析】由已知判断a,c,d都是负数,b为正数,再根据绝对值的意义,可推出各数的大小关系.
解:由题意知:a<0,b>0,c<0,d<0,
即a,c,d都是负数,b为正数,
又∵|a|>|b|>|c|>|d|,
∴a10.如果a是有理数,试比较|a|与-2a的大小.
【分析】由于不能确定a的正负,所以需分类讨论
解: 当a>0时,|a|>0,-2a<0,所以|a|>-2a;
当a=0时,|a|=0,-2a=0,所以|a|=-2a;
当a<0时,-2a>0,|a|=-a,因为-2a>-a,所以|a|<-2a.
达标检测
有理数大小的比较方法2---数的相对大小比较法
一般地,正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
有理数大小的比较方法1---数轴比较法
在数轴上表示的两个数,右边的数总比左边的数大.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
七上数学同步精品课件
人教版七年级上册
1.2.5 有理数大小的比较
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
第一章 有理数
1.掌握有理数大小的比较法则;(重点)
2.会比较有理数的大小,并能正确地使用“>”或“<”号连接; (重点)
3.能初步进行有理数大小比较的推理和书写.(难点)
如图,给出了未来一周中每天的最高气温和最低气温,其中最低气温是____℃,最高气温是____℃. 你能将这七天中每天的最低温度按从低到高的顺序排列吗?
-4,-3,-2,-1,0,1,2
-4
9
按照这个顺序排列的温度,在温度计上所对应的点是从下到上的. 按照这个顺序把这些数表示在数轴上,表示它们的各点的顺序是从左到右的.
-4,-3,-2,-1,0,1,2
数学中规定:在数轴上表示有理数,它从左到右的顺序,就是从小到大的顺序,即左边的数小于右边的数.
有理数大小的比较方法1---数轴比较法
在数轴上表示的两个数,右边的数总比左边的数大.
有没有最大的有理数 有没有最小的有理数 为什么
知识精讲
借助数轴比较有理数的大小
例1.在数轴上表示数-3,-4,-,2.5,0,并比较它们的大小,将它们按从小到大的顺序用“<”号连接.
解:
-3,-5,4,0在数轴上表示如图:
将它们按从小到大的顺序排列为:
-4 <-3 <-<0 <2.5
-5 -4 -3 -2 -1 0 1 2 3 4 5
●
●
●
●
●
-
2.5
因为在数轴上表示的两个数,右边的数总比左边的数大.
在数轴上表示下列各数:0,-3.5,-(-4),,-2.5,+5,并用“<”号连接.
解:
0,-3.5,-(-4),,-2.5,+5在数轴上表示如图:
化简:-(-4)=4,=
-
●
●
●
●
●
●
-
将它们按从小到大的顺序排列为:-3.5<-2.5<0<<-(-4)<+5.
1.对于正数、0、负数这三类数,它们之间有什么大小关系?
一般地,正数大于0,0大于负数,正数大于负数;
例如:1____0,0____-1,1____-1.
>
>
>
2.两个负数之间如何比较大小?
两个负数,绝对值大的反而小.
-3和-6如何比较大小呢?
有理数大小的比较方法2---数的相对大小比较法
一般地,正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
例2.比较下列各对数的大小.
(1) -(-1)和-(+2);(2)-和-;(3) -(-0.3)和|-|.
解:(1)先化简,-(-1)=1,-(+2)=-2
因为正数大于负数,
所以1>-2,即 -(-1)>-(+2)
(2)这是两个负数比较大小,先求它们的绝对值.
|-|= ,|-|= =
因为< ,即|-|<|-|,
所以->-
(3)先化简,-(-0.3)=0.3,|-|=
0.3< ,即-(-0.3)<|-|.
【点睛】异号两数比较大小,要考虑它们的正负;同号两数比较大小,要考虑它们的绝对值.
典例解析
比较两个负数大小的方法步骤是:
(1)如果需要化简,要先进行化简;
(2)再分别求出两个负数的绝对值;
(3)比较两个绝对值的大小;
(4)根据“两个负数,绝对值大的反而小”做出正确的判断.
比较下列各对数的大小:
(1)3和-5 (2) -3和-5 (3)-2.5和-|-2.25| (4)-和-
解:(1)因为正数大于负数,所以3>-5;
(2)因为|-3|<|-5|,所以-3>-5
(3)先化简,-|-2.25|=-2.25,因为|-2.5|>|-2.25|,
所以 -2.5<-|-2.25|
(4) |-|==,|-|==,因为>,所以->- .
例3.某公司抽检盒装牛奶的容量,超过标准容量的部分记为正数,不足的部分记为负数.从容量的角度看,以下四盒牛奶容量最接近标准的是( )
A. B. C. D.
【分析】解:A.+0.8的绝对值是0.8;B.-1.2的绝对值是1.2;C.-0.5的绝对值是0.5;D.+1的绝对值是1.
因为0.5<0.8<1<1.2,所以C选项的绝对值最小.
C
2020年末“霸王级”寒潮来袭,全国各地气温骤降,如图表示2021年元月某天山西省四个城市的天气情况.这一天最高气温最低的城市为( )
A.大同 B.太原 C.长治 D.晋城
A
例4.如果 ,试比较 的大小.
解:因为
所以
因为 ,
所以 ,
所以 , ,
所以 .
0
a
b
-b
-a
1.如图,点A表示的有理数是x,则x,-x,1的大小关系为( )
A.-x<x<1 B. x<-x<1 C. x<1<-x D. 1<-x<x
B
2.若0<x<1,则m、-m、的大小关系是( )
A.m<-m< B. -m<m< C. <m<-m D. <-m<
B
1.下列说法中正确的是( )
A.两个负数中,绝对值大的数就大 B.两个数中,绝对值较小的数就小
C.0没有绝对值 D.绝对值相等的两个数不一定相等
2.下列四组有理数大小的比较正确的是( )
A.-> B.->- C.->- D.>
D
D
3.若有理数a,b在数轴.上对应点的位置如图所示,则下列正确的是( )
A.|b|>-a B. |a|>-b C. b>a D. |a|>|b|
A
4.下列判断,正确的是( )
A.若a>b,则│a│>│b│ B.若│a│>│b│,则a>b
C.若a<b<0,则│a│<│b│ D.若a>b>0,则│a│>│b│
D
如a=1,b=-2
如a=-3,b=2
如a=-3,b=-2
5.绝对值大于1而不大于4的整数有__________________________.
-4、-3、-2、2、3、4
乙
6.厂家检测甲、乙、丙、丁四个足球的质量,超过标准质量的克数记为正数,不足标准质量的克数记为负数,结果如图所示,其中最接近标准质量的足球是______.
7.问题:比较-与+(-)的大小.
解:化简可得-=,+(-)=- ①.
因为=,=②
又==③
所以<-,④
所以-<+(-) ⑤.
本题是从______开始出现错误的(填序号).请给出正确的解题过程.
8.写出符合下列条件的数:
(1)大于﹣3且小于2的所有整数;
(2)绝对值大于2且小于5的所有负整数;
(3)在数轴上,与表示﹣1的点的距离为2的数.
解:(1)由题意得,大于﹣3且小于2的所有整数有﹣2、﹣1、0、1;
(2)根据题意得,绝对值大于2且小于5的所有负整数有:﹣3、﹣4;
(3)设在数轴上,与表示﹣1的点的距离为2的数为x,
则有:|x﹣(﹣1)|=2,
解得:x=1,或x=﹣3.
∴在数轴上,与表示﹣1的点的距离为2的所有数为1,﹣3.
9.若|a|=-a,|b|=b,|c|=-c,|d|=-d,a,b,c,d都不为零,并且|a|>|b|>|c|>|d|,请把a,b,c,d四个数从小到大用“<”号连结.
【分析】由已知判断a,c,d都是负数,b为正数,再根据绝对值的意义,可推出各数的大小关系.
解:由题意知:a<0,b>0,c<0,d<0,
即a,c,d都是负数,b为正数,
又∵|a|>|b|>|c|>|d|,
∴a
【分析】由于不能确定a的正负,所以需分类讨论
解: 当a>0时,|a|>0,-2a<0,所以|a|>-2a;
当a=0时,|a|=0,-2a=0,所以|a|=-2a;
当a<0时,-2a>0,|a|=-a,因为-2a>-a,所以|a|<-2a.
达标检测
有理数大小的比较方法2---数的相对大小比较法
一般地,正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
有理数大小的比较方法1---数轴比较法
在数轴上表示的两个数,右边的数总比左边的数大.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
