22.1.6 二次函数y=ax?+bx+c的图象和性质 课件(共27张PPT)
文档属性
| 名称 | 22.1.6 二次函数y=ax?+bx+c的图象和性质 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-05 17:54:55 | ||
图片预览







文档简介
(共27张PPT)
九上数学同步优质课件
人教版九年级上册
22.1.6 二次函数y=ax2+bx+c的图象和性质
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.会用配方法或公式法将一般式y=ax2+bx+c化成顶点式y=a(x-h)2+k.(难点)
2.会熟练求出二次函数一般式y=ax2+bx+c的顶点坐标、对称轴.(重点)
1.一般地,抛物线y=a(x-h)2+k与y=ax2的______相同,_____不同.
如 何
变 化
上加下减
左加右减
2.抛物线y=a(x-h)2+k有如下特点:
(1)当a>0时, 开口_____,当a<0时,开口_____;(2)对称轴是_______;
(3)顶点是__________.
形状
位置
向上
向下
直线x=h
(h,k)
3.抛物线y=-4(x+2)2-5的开口______,对称轴是直线_______,顶点坐标为_________;它可由抛物线y=-4x2向____(填“左”或“右”)平移____个单位,再向___(填“上”或“下”)平移____个单位得到;当x=___时,y有最___值,其值为___;当______时,y随着x的增大而增大,当______时,y随着x的增大而减小.
向下
x=-2
(-2,-5)
左
2
下
5
-2
大
-5
x<-2
x>-2
4.用配方法把下列二次多项式化为m(x+n)2+p的形式:
(1) x2-6x+5; (2)-3x2+5x+1.
解:原式=x2-6x+5
=x2-6x+9-9+5
=(x-3)2 -4
解:原式=-3(x2-x-)
=-3(x2-x+--)
=-3(x-)2-
=-3(x-)2+
1.怎样将 化成y=a(x-h)2+k的形式?
【点睛】二次函数一般式化为顶点式的步骤:(1)“提”:提出二次项系数;(2)“配”:括号内配成完全平方式;(3)“化”:化成顶点式.
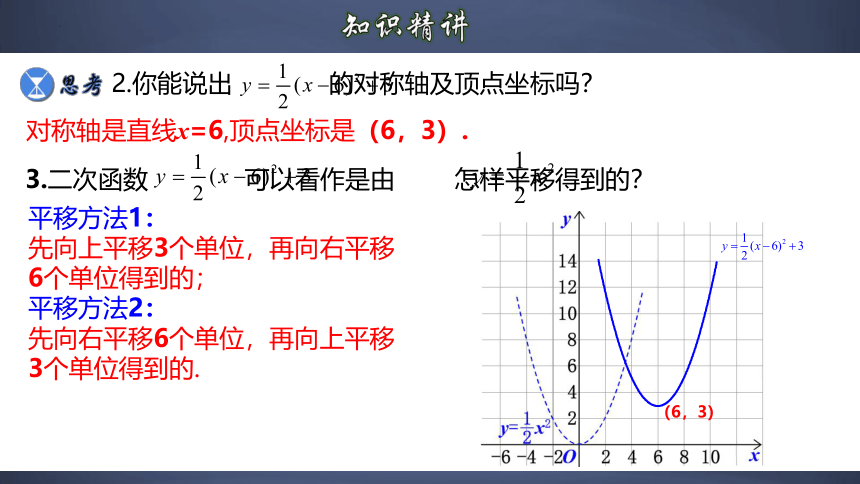
2.你能说出 的对称轴及顶点坐标吗?
对称轴是直线x=6,顶点坐标是(6,3).
3.二次函数 可以看作是由 怎样平移得到的?
平移方法1:
先向上平移3个单位,再向右平移6个单位得到的;
平移方法2:
先向右平移6个单位,再向上平移3个单位得到的.
(6,3)
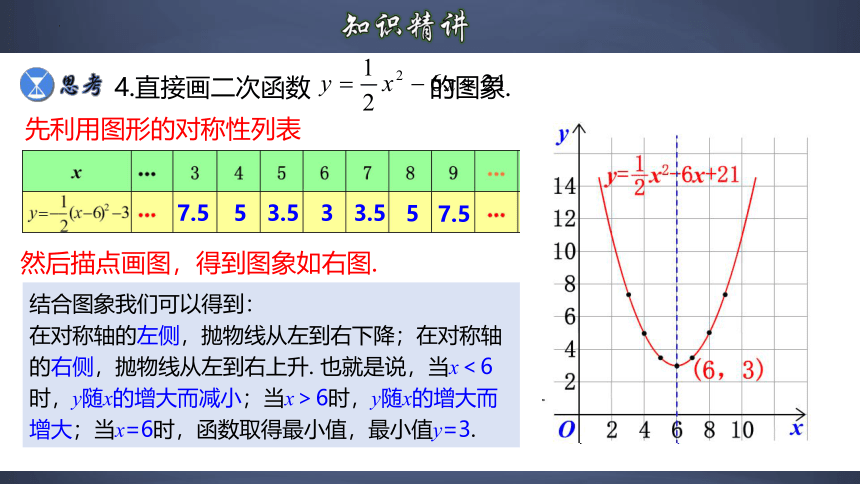
4.直接画二次函数 的图象.
先利用图形的对称性列表
7.5
5
3.5
3
3.5
5
7.5
然后描点画图,得到图象如右图.
结合图象我们可以得到:
在对称轴的左侧,抛物线从左到右下降;在对称轴的右侧,抛物线从左到右上升. 也就是说,当x<6时,y随x的增大而减小;当x>6时,y随x的增大而增大;当x=6时,函数取得最小值,最小值y=3.
你能用前面的方法讨论二次函数 的图象和性质吗?
配方
开口向下
顶点是(-1,3)
对称轴是直线x=-1
与y轴交点(0,1)
结合图象我们可以得到:
在对称轴的左侧,抛物线从左到右上升;在对称轴的右侧,抛物线从左到右下降. 也就是说,当x<-1时,y随x的增大而增大;当x>-1时,y随x的增大而减小;当x=-1时,函数取得最大值,最大值y=3.
一般地,二次函数y=ax2+bx+c(a≠0) 可以通过配方化成y=a(x-h)2+k的形式(顶点式).
配 方
对称轴是直线 ,顶点是 .
如果a>0时,那么当 时,y最小值= ;
如果a<0时,那么当 时,y最大值= .
如果a>0,当 时,y随x的增大而减小,当 时,y随x的增大而增大;
如果a<0,当 时,y随x的增大而增大,当 时,y随x的增大而减小.
例1.已知抛物线y=2x2-12x+13.
(1)当x为何值时,y有最小值,最小值是多少?
(2)当x为何值时,y随x的增大而减小;
(3)将该抛物线向右平移2个单位,再向上平移2个单位,请直接写出新抛物线的表达式.
解:∵y=2x2-12x+13=2(x2-2x+9)-5=2(x-3)2-5,
∴抛物线开口向上,顶点为(3,-5),对称轴为直线x=3.
(1)当x=3时,y有最小值,最小值为-5;
(2)当x<3时,y随x的增大而减小;
(3)新抛物线的表达式为y=2(x-5)2-3.
写出下列抛物线的开口方向、对称轴和顶点:
向上
向下
向下
向上
直线x=-
直线x=-1
直线x=2
直线x=4
(-,-)
(-1,1)
(2,0)
(4,-5)
x …… ﹣2 0 1 3 ……
y …… 6 ﹣4 ﹣6 ﹣4 ……
例2.如表中列出的一个二次函数的自变量x与函数y的几组对应值:
下列各选项中,正确的是( )
A.这个函数的图象开口向下
B.这个函数的图象与x轴无交点
C.这个函数的最小值小于﹣6
D.当x>﹣1,y的值随x值的增大而增大
C
已知二次函数y=ax2+bx+c的x、y的部分对应值如下表:
x -1 0 1 2 3
y 5 1 -1 -1 1
A.y轴 B.直线x= C. 直线x=2 D.直线x=
则该二次函数图象的对称轴为( )
D
例3.已知二次函数y=-x2+2bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是( )
A.b≥-1 B.b≤-1 C.b≥1 D.b≤1
解析:∵二次项系数为-1<0,∴抛物线开口向下,在对称轴右侧,y的值随x值的增大而减小,由题设可知,当x>1时,y的值随x值的增大而减小,∴抛物线y=-x2+2bx+c的对称轴应在直线x=1的左侧而抛物线y=-x2+2bx+c的对称轴 ,即b≤1,故选择D .
D
例4.如图,已知OA所在直线解析式为y=x,点P在线段OA上,PQ∥y轴且与抛物线y=x2-3x相交于点Q,则当PQ=3时,点Q的坐标为( )
A.(1,-2) B.(1,-2)或(2,-2)
C.(2,-2) D.(1,-2)或(3,0)
解:由OA所在直线解析式为=x,点P在线段OA上,设点P(x,x),
∵PQ∥y轴且与抛物线y=x2-3x相交于点Q,
∴Q(x,x2-3x),
∵PQ=3,点P在线段OA上,
∴x-(x2-3x)=3,
解得x=1或x=3,
∴点Q的坐标为(1,-2)或(3,0).
故选:D.
D
例5.已知二次函数y=x2-2x-3的自变量x1,x2,x3对应的函数值分别为y1,y2,y3.当-13时,y1,y2,y3三者之间的大小关系是( )
A.y1解:∵抛物线y=x2-2x-3=(x-1)2-4,
∴对称轴x=1,顶点坐标为(1,-4),
当y=0时,(x-1)2-4=0,
解得x=-1或x=3,
∴抛物线与x轴的两个交点坐标为:(-1,0),(3,0),
∴当-13时,y2D
2.抛物线的图象经过点A(-3,y1),B(1,y2),C(4,y3),则,,大小关系是( )
A.y2y1y3 B.y2y3y1 C.y1y3y2 D.y3y2y1
1.若点A(-2,y1),B(1,y2),C(3,y3)在二次函数图象上,则y1,y2,y3的大小关系是( )(用“”连接)
A.y3y2y1 B.y1y2y3 C.y2y1y3 D.y2y3y1
B
B
1.二次函数y=x2-2x+4化为y=a(x-h)2+k的形式,下列正确的是( )
A.y=(x-1)2+2 B.y=(x-1)2+3 C.y=(x-2)2+2 D.y=(x-2)2+4
2.二次函数y=x2+2x-5有( )
A.最大值-5 B.最小值-5 C.最大值-6 D.最小值-6
3.下列对二次函数y=x2+x的图象的描述,正确的是( )
A.对称轴是y轴 B.开口向下 C.经过原点 D.顶点在y轴右侧
B
D
C
4.在二次函数y=-x2+2x+1的图象中,若y随x的增大而增大,则x的取值范围是( )
A.x<1 B.x>1 C.x<-1 D.x>-1
A
5.抛物线y=2x2+3x-5与y轴的交点坐标是_________.
6.若抛物线y=x2+bx+1的对称轴在y轴右侧,则b的取值范围是_______.
7.若抛物线y=ax2-12x+3的对称轴是直线x=-3,则a的值为______.
8.将抛物线y=x2-2x向上平移3个单位,再向右平移4个单位得到的抛物线是________________.
9.当-1≤x≤3时,二次函数y=x2-4x+5有最大值m,则m=_______.
10.点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上,则m-n的最大值等于_______.
(0,-5)
b<0
-2
y=(x-5)2+2
10
-
配 方
对称轴是直线 ,顶点是 .
如果a>0时,那么当 时,y最小值= ;
如果a<0时,那么当 时,y最大值= .
如果a>0,当 时,y随x的增大而减小,当 时,y随x的增大而增大;
如果a<0,当 时,y随x的增大而增大,当 时,y随x的增大而减小.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
九上数学同步优质课件
人教版九年级上册
22.1.6 二次函数y=ax2+bx+c的图象和性质
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
1.会用配方法或公式法将一般式y=ax2+bx+c化成顶点式y=a(x-h)2+k.(难点)
2.会熟练求出二次函数一般式y=ax2+bx+c的顶点坐标、对称轴.(重点)
1.一般地,抛物线y=a(x-h)2+k与y=ax2的______相同,_____不同.
如 何
变 化
上加下减
左加右减
2.抛物线y=a(x-h)2+k有如下特点:
(1)当a>0时, 开口_____,当a<0时,开口_____;(2)对称轴是_______;
(3)顶点是__________.
形状
位置
向上
向下
直线x=h
(h,k)
3.抛物线y=-4(x+2)2-5的开口______,对称轴是直线_______,顶点坐标为_________;它可由抛物线y=-4x2向____(填“左”或“右”)平移____个单位,再向___(填“上”或“下”)平移____个单位得到;当x=___时,y有最___值,其值为___;当______时,y随着x的增大而增大,当______时,y随着x的增大而减小.
向下
x=-2
(-2,-5)
左
2
下
5
-2
大
-5
x<-2
x>-2
4.用配方法把下列二次多项式化为m(x+n)2+p的形式:
(1) x2-6x+5; (2)-3x2+5x+1.
解:原式=x2-6x+5
=x2-6x+9-9+5
=(x-3)2 -4
解:原式=-3(x2-x-)
=-3(x2-x+--)
=-3(x-)2-
=-3(x-)2+
1.怎样将 化成y=a(x-h)2+k的形式?
【点睛】二次函数一般式化为顶点式的步骤:(1)“提”:提出二次项系数;(2)“配”:括号内配成完全平方式;(3)“化”:化成顶点式.
2.你能说出 的对称轴及顶点坐标吗?
对称轴是直线x=6,顶点坐标是(6,3).
3.二次函数 可以看作是由 怎样平移得到的?
平移方法1:
先向上平移3个单位,再向右平移6个单位得到的;
平移方法2:
先向右平移6个单位,再向上平移3个单位得到的.
(6,3)
4.直接画二次函数 的图象.
先利用图形的对称性列表
7.5
5
3.5
3
3.5
5
7.5
然后描点画图,得到图象如右图.
结合图象我们可以得到:
在对称轴的左侧,抛物线从左到右下降;在对称轴的右侧,抛物线从左到右上升. 也就是说,当x<6时,y随x的增大而减小;当x>6时,y随x的增大而增大;当x=6时,函数取得最小值,最小值y=3.
你能用前面的方法讨论二次函数 的图象和性质吗?
配方
开口向下
顶点是(-1,3)
对称轴是直线x=-1
与y轴交点(0,1)
结合图象我们可以得到:
在对称轴的左侧,抛物线从左到右上升;在对称轴的右侧,抛物线从左到右下降. 也就是说,当x<-1时,y随x的增大而增大;当x>-1时,y随x的增大而减小;当x=-1时,函数取得最大值,最大值y=3.
一般地,二次函数y=ax2+bx+c(a≠0) 可以通过配方化成y=a(x-h)2+k的形式(顶点式).
配 方
对称轴是直线 ,顶点是 .
如果a>0时,那么当 时,y最小值= ;
如果a<0时,那么当 时,y最大值= .
如果a>0,当 时,y随x的增大而减小,当 时,y随x的增大而增大;
如果a<0,当 时,y随x的增大而增大,当 时,y随x的增大而减小.
例1.已知抛物线y=2x2-12x+13.
(1)当x为何值时,y有最小值,最小值是多少?
(2)当x为何值时,y随x的增大而减小;
(3)将该抛物线向右平移2个单位,再向上平移2个单位,请直接写出新抛物线的表达式.
解:∵y=2x2-12x+13=2(x2-2x+9)-5=2(x-3)2-5,
∴抛物线开口向上,顶点为(3,-5),对称轴为直线x=3.
(1)当x=3时,y有最小值,最小值为-5;
(2)当x<3时,y随x的增大而减小;
(3)新抛物线的表达式为y=2(x-5)2-3.
写出下列抛物线的开口方向、对称轴和顶点:
向上
向下
向下
向上
直线x=-
直线x=-1
直线x=2
直线x=4
(-,-)
(-1,1)
(2,0)
(4,-5)
x …… ﹣2 0 1 3 ……
y …… 6 ﹣4 ﹣6 ﹣4 ……
例2.如表中列出的一个二次函数的自变量x与函数y的几组对应值:
下列各选项中,正确的是( )
A.这个函数的图象开口向下
B.这个函数的图象与x轴无交点
C.这个函数的最小值小于﹣6
D.当x>﹣1,y的值随x值的增大而增大
C
已知二次函数y=ax2+bx+c的x、y的部分对应值如下表:
x -1 0 1 2 3
y 5 1 -1 -1 1
A.y轴 B.直线x= C. 直线x=2 D.直线x=
则该二次函数图象的对称轴为( )
D
例3.已知二次函数y=-x2+2bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是( )
A.b≥-1 B.b≤-1 C.b≥1 D.b≤1
解析:∵二次项系数为-1<0,∴抛物线开口向下,在对称轴右侧,y的值随x值的增大而减小,由题设可知,当x>1时,y的值随x值的增大而减小,∴抛物线y=-x2+2bx+c的对称轴应在直线x=1的左侧而抛物线y=-x2+2bx+c的对称轴 ,即b≤1,故选择D .
D
例4.如图,已知OA所在直线解析式为y=x,点P在线段OA上,PQ∥y轴且与抛物线y=x2-3x相交于点Q,则当PQ=3时,点Q的坐标为( )
A.(1,-2) B.(1,-2)或(2,-2)
C.(2,-2) D.(1,-2)或(3,0)
解:由OA所在直线解析式为=x,点P在线段OA上,设点P(x,x),
∵PQ∥y轴且与抛物线y=x2-3x相交于点Q,
∴Q(x,x2-3x),
∵PQ=3,点P在线段OA上,
∴x-(x2-3x)=3,
解得x=1或x=3,
∴点Q的坐标为(1,-2)或(3,0).
故选:D.
D
例5.已知二次函数y=x2-2x-3的自变量x1,x2,x3对应的函数值分别为y1,y2,y3.当-1
A.y1
∴对称轴x=1,顶点坐标为(1,-4),
当y=0时,(x-1)2-4=0,
解得x=-1或x=3,
∴抛物线与x轴的两个交点坐标为:(-1,0),(3,0),
∴当-1
2.抛物线的图象经过点A(-3,y1),B(1,y2),C(4,y3),则,,大小关系是( )
A.y2y1y3 B.y2y3y1 C.y1y3y2 D.y3y2y1
1.若点A(-2,y1),B(1,y2),C(3,y3)在二次函数图象上,则y1,y2,y3的大小关系是( )(用“”连接)
A.y3y2y1 B.y1y2y3 C.y2y1y3 D.y2y3y1
B
B
1.二次函数y=x2-2x+4化为y=a(x-h)2+k的形式,下列正确的是( )
A.y=(x-1)2+2 B.y=(x-1)2+3 C.y=(x-2)2+2 D.y=(x-2)2+4
2.二次函数y=x2+2x-5有( )
A.最大值-5 B.最小值-5 C.最大值-6 D.最小值-6
3.下列对二次函数y=x2+x的图象的描述,正确的是( )
A.对称轴是y轴 B.开口向下 C.经过原点 D.顶点在y轴右侧
B
D
C
4.在二次函数y=-x2+2x+1的图象中,若y随x的增大而增大,则x的取值范围是( )
A.x<1 B.x>1 C.x<-1 D.x>-1
A
5.抛物线y=2x2+3x-5与y轴的交点坐标是_________.
6.若抛物线y=x2+bx+1的对称轴在y轴右侧,则b的取值范围是_______.
7.若抛物线y=ax2-12x+3的对称轴是直线x=-3,则a的值为______.
8.将抛物线y=x2-2x向上平移3个单位,再向右平移4个单位得到的抛物线是________________.
9.当-1≤x≤3时,二次函数y=x2-4x+5有最大值m,则m=_______.
10.点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上,则m-n的最大值等于_______.
(0,-5)
b<0
-2
y=(x-5)2+2
10
-
配 方
对称轴是直线 ,顶点是 .
如果a>0时,那么当 时,y最小值= ;
如果a<0时,那么当 时,y最大值= .
如果a>0,当 时,y随x的增大而减小,当 时,y随x的增大而增大;
如果a<0,当 时,y随x的增大而增大,当 时,y随x的增大而减小.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
