1.3 交集、并集 同步练习-2022-2023学年高一上学期数学苏教版(2019)必修第一册(Word版含答案)
文档属性
| 名称 | 1.3 交集、并集 同步练习-2022-2023学年高一上学期数学苏教版(2019)必修第一册(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 56.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-15 21:22:27 | ||
图片预览



文档简介
《第三节 交集、并集》同步练习
一、基础巩固
知识点1 交集
1.[2022江苏省响水中学高一下期初]已知集合A={-1,0,1,2,3,4,5},集合B={x|-3A.{-1,0,1,2,3} B.{0,1,2,3}
C.{-1,0,1,2} D.{-1,0,1,2,3,4}
2.[2022江苏扬州高一上期中]设集合A={x|0≤x≤2},B={x|1≤x≤3},则A∩B=( )
A.{1,2} B.{1,2,3}
C.{x|1≤x≤2} D.{x|0≤x≤3}
3.[2022江苏镇江六校高一上期中联考]已知A={x|x=2k,k∈Z},B={x|x=4n,n∈Z},则A∩B=( )
A. B.A C.B D.Z
4.设集合A={(x,y)|x-2y=1},B={(x,y)|x+y=2},则A∩B=( )
A. B.{(,)}
C.{(,)} D.{,}
5.(多选)[2022广东广州高一期中]设集合A={2,4,2x},B={2,x2},且A∩B=B,则实数x的值可以为( )
A.2 B.-2 C.0 D.-1
6.已知集合A={x|2(1)若A∩B={x|3(2)若A∩B= ,求实数a的取值范围.
知识点2 并集
7.[2022江苏连云港高一期末]已知集合A={x|1≤x≤3},B={x|2A.{x|2C.{x|1≤x<4} D.{x|2≤x<4}
8.[2022江苏省苏州实验中学高一上月考]已知集合A={x|x2-3x=0},B={1,2,3},则A∪B=( )
A.{3} B.{0,1,2,3}
C.{1,2,-3} D.{1,2,3}
9.[2021北京五中高一上阶段测试]满足条件M∪{1}={1,2,3}的集合M的个数是( )
A.1 B.2
C.3 D.4
10.(多选)[2022山东乳山高一期中]设集合A={x|x2-7x+12=0},B={x|ax-1=0},若A∪B=A,则实数a的值可以为( )
A. B.0
C.3 D.
11.已知集合A={x|-5(1)若B={x|x≥m},A∪B=B,求实数m的取值范围;
(2)若B={x|xm},A∪B=R,求实数m的取值范围.
知识点3 区间的表示
12.区间(-3,2]用集合可表示为( )
A.{-2,-1,0,1,2} B.{x|-3C.{x|-313.用区间表示下列集合:
(1){x|x>-1}= ;
(2){x|2(3){x|2≤x≤4}= ;
(4){x|-3≤x<0或2≤x<4}= ;
(5){x|-214.若(a,3a-1]为一确定区间,则实数a的取值范围是 .
知识点4 交集、并集、补集的综合运算与应用
15.[2022江苏徐州高一上期末]已知集合A={x|-1A. B.{-1,2}
C.{-2,4} D.{-2,-1,4}
16.已知集合A={x|x2-2x-3=0},B={1,a},若A∩B={3},则A∪B=( )
A.{1,3} B.{-1,3}
C.{-1,1,3} D.{-3,-1,3}
17.设A,B是非空集合,定义A*B={x|x∈A∪B且x A∩B}.已知A=[0,3],B=[1,+∞),则A*B=( )
A.[1,3) B.[0,1)∪(3,+∞)
C.[1,3] D.[0,1]∪[3,+∞)
18.(多选)[2022江苏高一上百校大联考]已知集合U={1,2,3,4,5,6},M={2,3,5},N={1,3},则( )
A.M∪N={1,2,3,5}
B.( UM)∩( UN)={3}
C.( UN)∩M={2,5}
D.( UM)∪N={1,3,4,6}
19.[2021安徽合肥一中高一上段考]设全集U=R,A=(2,5],B=[-1,3),则图中阴影部分表示的集合为( )
A.[3,5) B.[3,5]
C.[-1,5] D.(2,3)
20.设集合A={x|-1≤x≤2},B={x|m-121.[2022江苏宿迁高一上期中]已知{3} B {3,4,5},写出一个满足条件的集合B,补充在下列问题中的横线上,并作答.
问题:已知U={x|x∈N*,且x<10},A={x|x是小于10的正偶数},B= .求A∪B,A∩ UB.
22.[2022陕西西安高新一中高一上期中]已知集合A={x|-33},C={x|-2-3.
(1)求A∩B;
(2)若(A∪B)∩C=C,求实数m的取值范围.
二、能力提升
1.(多选)若集合M={x|-3A.M∩N B. RM
C. R(M∩N) D. R(M∪N)
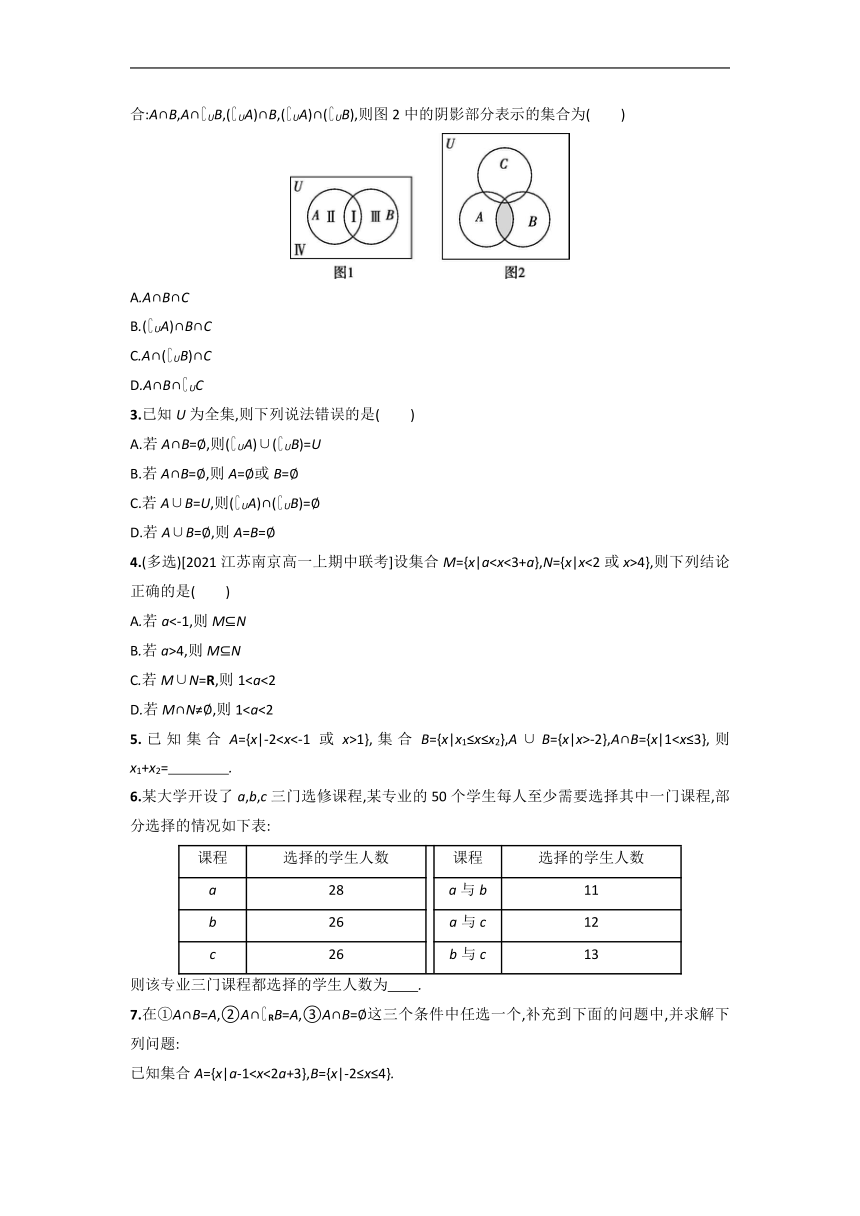
2.[2022江苏南京金陵中学高三上期中]图1中的四块区域Ⅰ,Ⅱ,Ⅲ,Ⅳ分别表示下列四个集合:A∩B,A∩ UB,( UA)∩B,( UA)∩( UB),则图2中的阴影部分表示的集合为( )
A.A∩B∩C
B.( UA)∩B∩C
C.A∩( UB)∩C
D.A∩B∩ UC
3.已知U为全集,则下列说法错误的是( )
A.若A∩B= ,则( UA)∪( UB)=U
B.若A∩B= ,则A= 或B=
C.若A∪B=U,则( UA)∩( UB)=
D.若A∪B= ,则A=B=
4.(多选)[2021江苏南京高一上期中联考]设集合M={x|a4},则下列结论正确的是( )
A.若a<-1,则M N
B.若a>4,则M N
C.若M∪N=R,则1D.若M∩N≠ ,则15.已知集合A={x|-21},集合B={x|x1≤x≤x2},A∪B={x|x>-2},A∩B={x|16.某大学开设了a,b,c三门选修课程,某专业的50个学生每人至少需要选择其中一门课程,部分选择的情况如下表:
课程 选择的学生人数 课程 选择的学生人数
a 28 a与b 11
b 26 a与c 12
c 26 b与c 13
则该专业三门课程都选择的学生人数为 .
7.在①A∩B=A,②A∩ RB=A,③A∩B= 这三个条件中任选一个,补充到下面的问题中,并求解下列问题:
已知集合A={x|a-1(1)当a=2时,求A∪B;
(2)若 ,求实数a的取值范围.
8.已知集合A={x|-2(1)若A∪B=A,求实数m的取值范围;
(2)若A∩B={x|a参考答案
一、基础巩固
1.A 2.C 3.C 4.C 5.BC
6.(1)因为A∩B={x|3(2)因为A∩B= ,所以可分两种情况讨论:B= ,B≠ .
当B= 时,有a≥3a,解得a≤0;
当B≠ 时,有解得a≥4或0综上,实数a的取值范围是{a|a≤或a≥4}.
7.C 8.B
9.B 由题意,可知满足条件的集合M必须包含元素2,3.1可以是M中的元素,也可以不是,所以满足条件的集合M为{2,3}或{1,2,3}.
10.ABD A={x|x2-7x+12=0}={3,4}.由A∪B=A,得B A.当B= 时,a=0,B A成立;当B≠ 时,B={3}或B={4},得a=或a=.故选ABD.
11.(1)由A∪B=B,知A B,所以m≤-5,
即实数m的取值范围为{m|m≤-5}.
(2)由题意,得解得-3即实数m的取值范围为{m|-312.C
13.(1)(-1,+∞);(2)(2,5];(3)[2,4];
(4)[-3,0)∪[2,4);(5)(-2,0)∪(0,2]
14.(,+∞)
15.D 16.C 17.B 18.ACD 19.B
20.{m|-21.满足{3} B {3,4,5}的集合B={3,4}或{3,5}或{3,4,5}.
方案一 B={3,4}.
由题意可得U={1,2,3,4,5,6,7,8,9},
A={2,4,6,8},
可得A∪B={2,3,4,6,8}.
因为 UB={1,2,5,6,7,8,9},
所以A∩ UB={2,6,8}.
方案二 B={3,5}.
由题意可得U={1,2,3,4,5,6,7,8,9},
A={2,4,6,8},
可得A∪B={2,3,4,5,6,8}.
因为 UB={1,2,4,6,7,8,9},
所以A∩ UB={2,4,6,8}.
方案三 B={3,4,5}.
由题意可得U={1,2,3,4,5,6,7,8,9},
A={2,4,6,8},可得A∪B={2,3,4,5,6,8}.
因为 UB={1,2,6,7,8,9},
所以A∩ UB={2,6,8}.
22.(1)因为A={x|-33},
所以A∩B={x|-3(2)由题意,得A∪B={x|x<1或x>3}.
因为(A∪B)∩C=C,所以C A∪B.
因为m>-3,所以C≠ ,所以m+1≤1,解得m≤0,
所以实数m的取值范围是{m|-3二、能力提升
1.BC 2.D 3.B 4.ABC
5.2
6.6
7.(1)当a=2时,A={x|1又B={x|-2≤x≤4},
所以A∪B={x|-2≤x<7}.
(2)方案一 选择条件①.
若A∩B=A,则A B.
当A= 时,a-1≥2a+3,即a≤-4;
当A≠ 时,2a+3>a-1,即a>-4,
此时解得-1≤a≤.
综上,实数a的取值范围是(-∞,-4]∪[-1,].
方案二 选择条件②.
若A∩ RB=A,则A RB,易知 RB={x|x<-2或x>4}.
当A= 时,a-1≥2a+3,即a≤-4;
当A≠ 时,2a+3>a-1,即a>-4,
此时或解得-4综上,实数a的取值范围是(-∞,-]∪[5,+∞).
方案三 选择条件③.
若A∩B= ,则
当A= 时,a-1≥2a+3,即a≤-4;
当A≠ 时,2a+3>a-1,即a>-4,
此时或解得-4综上,实数a的取值范围是(-∞,-]∪[5,+∞).
8.(1)由A∪B=A,知B A.
①当B= 时,2m-1≥m+3,解得m≥4;
②当B≠ 时,有解得-≤m<4.
所以实数m的取值范围为[-,+∞).
(2)因为A={x|-2①当A∩B=B时,有
解得m=1;
②当A∩B={x|2m-1有无解;
③当A∩B={x|-2有解得m=-2.
综上,实数m的值为-2或1.
一、基础巩固
知识点1 交集
1.[2022江苏省响水中学高一下期初]已知集合A={-1,0,1,2,3,4,5},集合B={x|-3
C.{-1,0,1,2} D.{-1,0,1,2,3,4}
2.[2022江苏扬州高一上期中]设集合A={x|0≤x≤2},B={x|1≤x≤3},则A∩B=( )
A.{1,2} B.{1,2,3}
C.{x|1≤x≤2} D.{x|0≤x≤3}
3.[2022江苏镇江六校高一上期中联考]已知A={x|x=2k,k∈Z},B={x|x=4n,n∈Z},则A∩B=( )
A. B.A C.B D.Z
4.设集合A={(x,y)|x-2y=1},B={(x,y)|x+y=2},则A∩B=( )
A. B.{(,)}
C.{(,)} D.{,}
5.(多选)[2022广东广州高一期中]设集合A={2,4,2x},B={2,x2},且A∩B=B,则实数x的值可以为( )
A.2 B.-2 C.0 D.-1
6.已知集合A={x|2
知识点2 并集
7.[2022江苏连云港高一期末]已知集合A={x|1≤x≤3},B={x|2
8.[2022江苏省苏州实验中学高一上月考]已知集合A={x|x2-3x=0},B={1,2,3},则A∪B=( )
A.{3} B.{0,1,2,3}
C.{1,2,-3} D.{1,2,3}
9.[2021北京五中高一上阶段测试]满足条件M∪{1}={1,2,3}的集合M的个数是( )
A.1 B.2
C.3 D.4
10.(多选)[2022山东乳山高一期中]设集合A={x|x2-7x+12=0},B={x|ax-1=0},若A∪B=A,则实数a的值可以为( )
A. B.0
C.3 D.
11.已知集合A={x|-5
(2)若B={x|x
知识点3 区间的表示
12.区间(-3,2]用集合可表示为( )
A.{-2,-1,0,1,2} B.{x|-3
(1){x|x>-1}= ;
(2){x|2
(4){x|-3≤x<0或2≤x<4}= ;
(5){x|-2
知识点4 交集、并集、补集的综合运算与应用
15.[2022江苏徐州高一上期末]已知集合A={x|-1
C.{-2,4} D.{-2,-1,4}
16.已知集合A={x|x2-2x-3=0},B={1,a},若A∩B={3},则A∪B=( )
A.{1,3} B.{-1,3}
C.{-1,1,3} D.{-3,-1,3}
17.设A,B是非空集合,定义A*B={x|x∈A∪B且x A∩B}.已知A=[0,3],B=[1,+∞),则A*B=( )
A.[1,3) B.[0,1)∪(3,+∞)
C.[1,3] D.[0,1]∪[3,+∞)
18.(多选)[2022江苏高一上百校大联考]已知集合U={1,2,3,4,5,6},M={2,3,5},N={1,3},则( )
A.M∪N={1,2,3,5}
B.( UM)∩( UN)={3}
C.( UN)∩M={2,5}
D.( UM)∪N={1,3,4,6}
19.[2021安徽合肥一中高一上段考]设全集U=R,A=(2,5],B=[-1,3),则图中阴影部分表示的集合为( )
A.[3,5) B.[3,5]
C.[-1,5] D.(2,3)
20.设集合A={x|-1≤x≤2},B={x|m-1
问题:已知U={x|x∈N*,且x<10},A={x|x是小于10的正偶数},B= .求A∪B,A∩ UB.
22.[2022陕西西安高新一中高一上期中]已知集合A={x|-3
(1)求A∩B;
(2)若(A∪B)∩C=C,求实数m的取值范围.
二、能力提升
1.(多选)若集合M={x|-3
C. R(M∩N) D. R(M∪N)
2.[2022江苏南京金陵中学高三上期中]图1中的四块区域Ⅰ,Ⅱ,Ⅲ,Ⅳ分别表示下列四个集合:A∩B,A∩ UB,( UA)∩B,( UA)∩( UB),则图2中的阴影部分表示的集合为( )
A.A∩B∩C
B.( UA)∩B∩C
C.A∩( UB)∩C
D.A∩B∩ UC
3.已知U为全集,则下列说法错误的是( )
A.若A∩B= ,则( UA)∪( UB)=U
B.若A∩B= ,则A= 或B=
C.若A∪B=U,则( UA)∩( UB)=
D.若A∪B= ,则A=B=
4.(多选)[2021江苏南京高一上期中联考]设集合M={x|a
A.若a<-1,则M N
B.若a>4,则M N
C.若M∪N=R,则1
课程 选择的学生人数 课程 选择的学生人数
a 28 a与b 11
b 26 a与c 12
c 26 b与c 13
则该专业三门课程都选择的学生人数为 .
7.在①A∩B=A,②A∩ RB=A,③A∩B= 这三个条件中任选一个,补充到下面的问题中,并求解下列问题:
已知集合A={x|a-1
(2)若 ,求实数a的取值范围.
8.已知集合A={x|-2
(2)若A∩B={x|a
一、基础巩固
1.A 2.C 3.C 4.C 5.BC
6.(1)因为A∩B={x|3
当B= 时,有a≥3a,解得a≤0;
当B≠ 时,有解得a≥4或0
7.C 8.B
9.B 由题意,可知满足条件的集合M必须包含元素2,3.1可以是M中的元素,也可以不是,所以满足条件的集合M为{2,3}或{1,2,3}.
10.ABD A={x|x2-7x+12=0}={3,4}.由A∪B=A,得B A.当B= 时,a=0,B A成立;当B≠ 时,B={3}或B={4},得a=或a=.故选ABD.
11.(1)由A∪B=B,知A B,所以m≤-5,
即实数m的取值范围为{m|m≤-5}.
(2)由题意,得解得-3
13.(1)(-1,+∞);(2)(2,5];(3)[2,4];
(4)[-3,0)∪[2,4);(5)(-2,0)∪(0,2]
14.(,+∞)
15.D 16.C 17.B 18.ACD 19.B
20.{m|-
方案一 B={3,4}.
由题意可得U={1,2,3,4,5,6,7,8,9},
A={2,4,6,8},
可得A∪B={2,3,4,6,8}.
因为 UB={1,2,5,6,7,8,9},
所以A∩ UB={2,6,8}.
方案二 B={3,5}.
由题意可得U={1,2,3,4,5,6,7,8,9},
A={2,4,6,8},
可得A∪B={2,3,4,5,6,8}.
因为 UB={1,2,4,6,7,8,9},
所以A∩ UB={2,4,6,8}.
方案三 B={3,4,5}.
由题意可得U={1,2,3,4,5,6,7,8,9},
A={2,4,6,8},可得A∪B={2,3,4,5,6,8}.
因为 UB={1,2,6,7,8,9},
所以A∩ UB={2,6,8}.
22.(1)因为A={x|-3
所以A∩B={x|-3
因为(A∪B)∩C=C,所以C A∪B.
因为m>-3,所以C≠ ,所以m+1≤1,解得m≤0,
所以实数m的取值范围是{m|-3
1.BC 2.D 3.B 4.ABC
5.2
6.6
7.(1)当a=2时,A={x|1
所以A∪B={x|-2≤x<7}.
(2)方案一 选择条件①.
若A∩B=A,则A B.
当A= 时,a-1≥2a+3,即a≤-4;
当A≠ 时,2a+3>a-1,即a>-4,
此时解得-1≤a≤.
综上,实数a的取值范围是(-∞,-4]∪[-1,].
方案二 选择条件②.
若A∩ RB=A,则A RB,易知 RB={x|x<-2或x>4}.
当A= 时,a-1≥2a+3,即a≤-4;
当A≠ 时,2a+3>a-1,即a>-4,
此时或解得-4
方案三 选择条件③.
若A∩B= ,则
当A= 时,a-1≥2a+3,即a≤-4;
当A≠ 时,2a+3>a-1,即a>-4,
此时或解得-4
8.(1)由A∪B=A,知B A.
①当B= 时,2m-1≥m+3,解得m≥4;
②当B≠ 时,有解得-≤m<4.
所以实数m的取值范围为[-,+∞).
(2)因为A={x|-2
解得m=1;
②当A∩B={x|2m-1
③当A∩B={x|-2
综上,实数m的值为-2或1.
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
