4.3.1对数的概念 学案(Word版无答案)
文档属性
| 名称 | 4.3.1对数的概念 学案(Word版无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 97.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-16 08:24:53 | ||
图片预览


文档简介
4.3.1对数的概念
课标要求 理解对数的概念,培养数学抽象思维及数学运算能力
学习目标 1、理解对数的概念,掌握对数的性质,能进行简单的对数计算. 2、理解指数式与对数式的等价关系,会进行对数式与指数式的互化 3、理解常用对数、自然对数的概念及记法.
学情分析 教学重点:理解对数的概念,掌握指数式与对数式的等价关系,会进行对数式与指数式的互化。
教学难点:掌握对数的性质,能进行简单的对数计算
学习内容与问题设计 学习过程设计
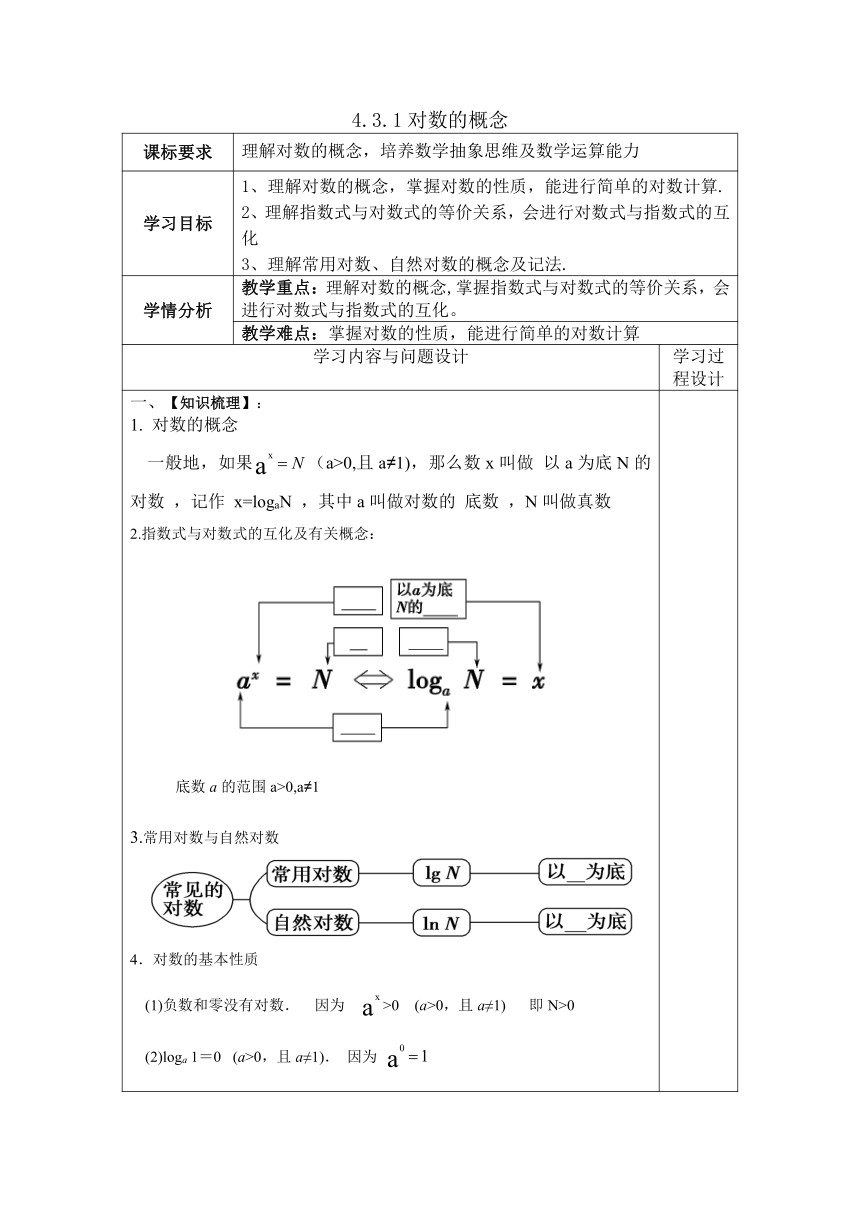
一、【知识梳理】: 对数的概念 一般地,如果(a>0,且a≠1),那么数x叫做 以a为底N的对数 ,记作 x=logaN ,其中a叫做对数的 底数 ,N叫做真数 2.指数式与对数式的互化及有关概念: 底数a的范围a>0,a≠1a_ _____________a 3.常用对数与自然对数 4.对数的基本性质 (1)负数和零没有对数. 因为 >0 (a>0,且a≠1) 即N>0 (2)loga 1=00 (a>0,且a≠1). 因为 (3)logaa=11 (a>0,且a≠1) 因为 二、【合作探究】: 探究一:指数式与对数式的互化 【例1】 将下列对数形式化为指数形式或将指数形式化为对数形式: (1)3-2=; (2)=16; 解: (1)3-2=; (2)-2=16; (3)log27=-3; (4)log64=-6. 探究二:利用指数式与对数式的关系求值 【例2】 求下列各式中的x的值: (1)log64x=-; (2)logx 8=6; (3)lg 100=x; (4)-ln e2=x. .[解] (1)x=(64)=(43)=4-2=. (2)x6=8,所以x=(x6)=8=(23) =2=. (3)10x=100=102,于是x=2. (4)由-ln e2=x,得-x=ln e2,即e-x=e2,所以x=-2. 规律方法:要求对数的值,设对数为某一未知数,将对数式化为指数式,再利用指数幂的运算性质求解。 计算(1)log927 (2) (3) (4) 答案:(1) (2)- (3)- (4) 16 探究三:应用对数的基本性质求值 A.10 B.13 C.100 D.±100 解: log5(2x-1)=2 2x-1= ,2x-1=25 x=13 探究四:利用对数恒等式,求下列各式的值。 (1) (2) (3) (4)log3(log28) 解:(1)3 (2) (3)=125 (4)1
反思提升
课标要求 理解对数的概念,培养数学抽象思维及数学运算能力
学习目标 1、理解对数的概念,掌握对数的性质,能进行简单的对数计算. 2、理解指数式与对数式的等价关系,会进行对数式与指数式的互化 3、理解常用对数、自然对数的概念及记法.
学情分析 教学重点:理解对数的概念,掌握指数式与对数式的等价关系,会进行对数式与指数式的互化。
教学难点:掌握对数的性质,能进行简单的对数计算
学习内容与问题设计 学习过程设计
一、【知识梳理】: 对数的概念 一般地,如果(a>0,且a≠1),那么数x叫做 以a为底N的对数 ,记作 x=logaN ,其中a叫做对数的 底数 ,N叫做真数 2.指数式与对数式的互化及有关概念: 底数a的范围a>0,a≠1a_ _____________a 3.常用对数与自然对数 4.对数的基本性质 (1)负数和零没有对数. 因为 >0 (a>0,且a≠1) 即N>0 (2)loga 1=00 (a>0,且a≠1). 因为 (3)logaa=11 (a>0,且a≠1) 因为 二、【合作探究】: 探究一:指数式与对数式的互化 【例1】 将下列对数形式化为指数形式或将指数形式化为对数形式: (1)3-2=; (2)=16; 解: (1)3-2=; (2)-2=16; (3)log27=-3; (4)log64=-6. 探究二:利用指数式与对数式的关系求值 【例2】 求下列各式中的x的值: (1)log64x=-; (2)logx 8=6; (3)lg 100=x; (4)-ln e2=x. .[解] (1)x=(64)=(43)=4-2=. (2)x6=8,所以x=(x6)=8=(23) =2=. (3)10x=100=102,于是x=2. (4)由-ln e2=x,得-x=ln e2,即e-x=e2,所以x=-2. 规律方法:要求对数的值,设对数为某一未知数,将对数式化为指数式,再利用指数幂的运算性质求解。 计算(1)log927 (2) (3) (4) 答案:(1) (2)- (3)- (4) 16 探究三:应用对数的基本性质求值 A.10 B.13 C.100 D.±100 解: log5(2x-1)=2 2x-1= ,2x-1=25 x=13 探究四:利用对数恒等式,求下列各式的值。 (1) (2) (3) (4)log3(log28) 解:(1)3 (2) (3)=125 (4)1
反思提升
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
