4.4 课题学习 设计制作长方体形状的包装纸盒同步跟踪测试(含答案)
文档属性
| 名称 | 4.4 课题学习 设计制作长方体形状的包装纸盒同步跟踪测试(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 310.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-16 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
4.4 课题学习 设计制作长方体形状的包装纸盒
一、选择题
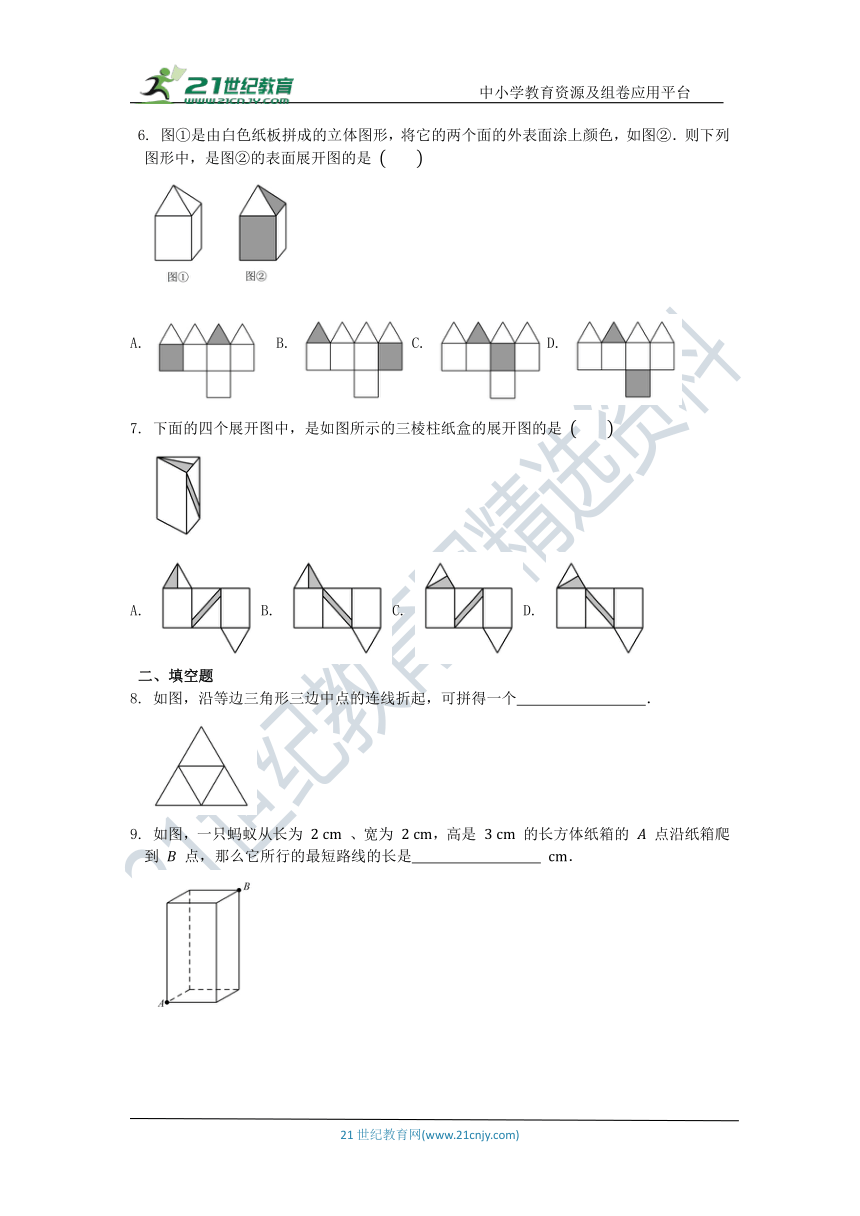
1. 下图中各硬纸片,不可以沿虚线折叠成长方体纸盒的是
A. ①② B. ②③ C. ③④ D. ①④
2. 下列平面图形经过折叠不能围成棱柱的是
A. B. C. D.
3. 下列四个图形中是三棱柱的表面展开图的是
A. B. C. D.
4. 下列四个图形中,是三棱柱的平面展开图的是
A. B. C. D.
5. 图 是下列几何体 的平面展开图.
A. B. C. D.
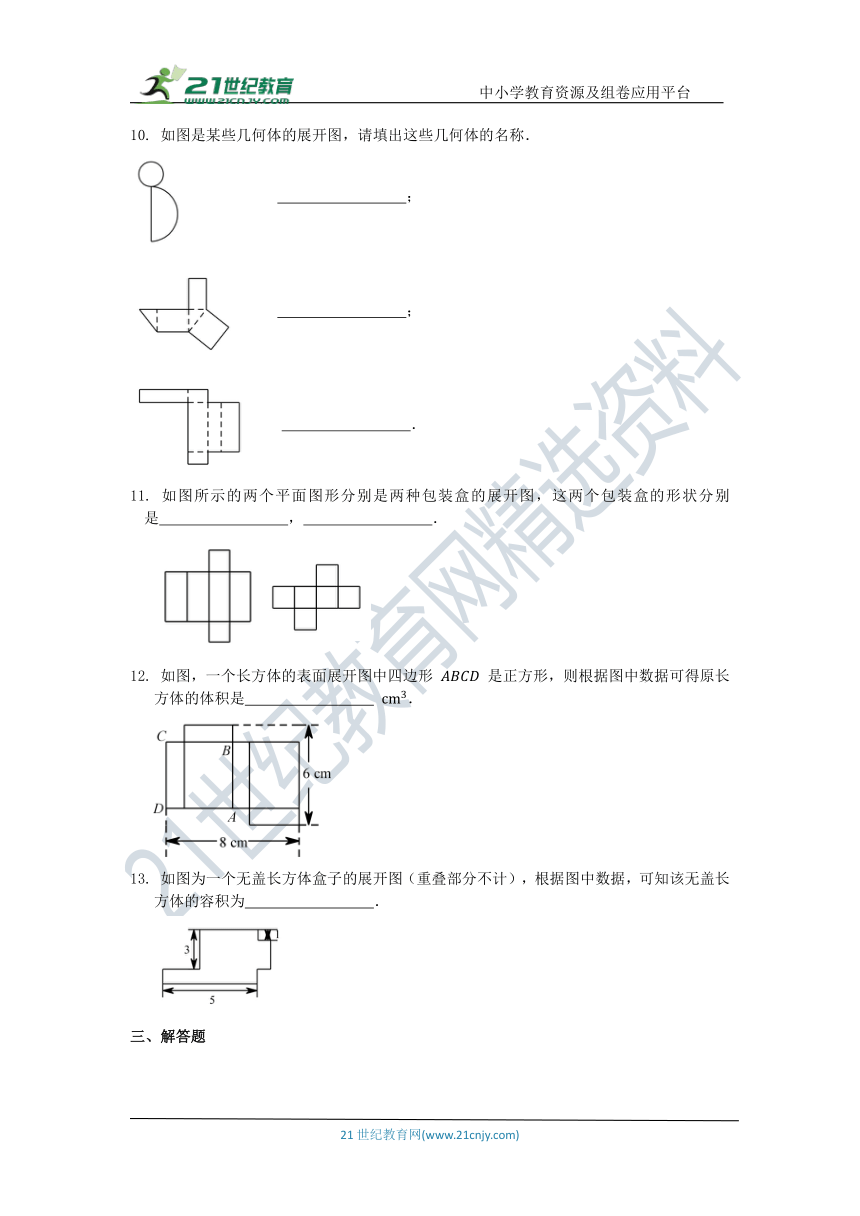
6. 图①是由白色纸板拼成的立体图形,将它的两个面的外表面涂上颜色,如图②.则下列图形中,是图②的表面展开图的是
A. B. C. D.
7. 下面的四个展开图中,是如图所示的三棱柱纸盒的展开图的是
A. B. C. D.
二、填空题
8. 如图,沿等边三角形三边中点的连线折起,可拼得一个 .
9. 如图,一只蚂蚁从长为 、宽为 ,高是 的长方体纸箱的 点沿纸箱爬到 点,那么它所行的最短路线的长是 .
10. 如图是某些几何体的展开图,请填出这些几何体的名称.
;
;
.
11. 如图所示的两个平面图形分别是两种包装盒的展开图,这两个包装盒的形状分别是 , .
12. 如图,一个长方体的表面展开图中四边形 是正方形,则根据图中数据可得原长方体的体积是 .
13. 如图为一个无盖长方体盒子的展开图(重叠部分不计),根据图中数据,可知该无盖长方体的容积为 .
三、解答题
14. 要制作一个长 、宽 、高 的长方体纸盒,先要在纸板上画出展开图,而展开方式不同,展开图的周长是否相同呢 若不相同,在什么情况下,平面展开图周长最小 请你画出此时它的平面展开图.
15. 如图是一长方体的展开图,每一面内都标注了字母(标字母的面是外表面),根据要求回答问题:
(1)如果 面在多面体的左面,那么 面在哪里
(2) 面和哪个面是相对的面
(3)如果 面在前面,从上面看到的是 面,那么从左面看是哪一面
(4)如果 面在后面,从左面看是 面,那么前面是哪个面
(5)如果 面在右面,从下面看是 面,那么 面在哪里
16. 如图,小华用若干个正方形和长方形准备拼成一个长方体的展开图.拼完后,小华看来看去总觉得所拼图形似乎存在问题.
(1)请你帮小华分析一下拼图是否存在问题:若有多余块,则把图中多余部分涂黑;若还缺少,则直接在原图中补全.
(2)若图中的正方形边长为 ,长方形的长为 ,宽为 ,请直接写出修正后所折叠而成的长方体的容积:
17. 给出一张正方形纸片(见图),要求将其剪拼成一个上、下底面均为正方形的直四棱柱模型,使它的表面积与原正方形的面积相等.请设计一种剪拼方法,在图中用虚线标示,并作简要说明.
18. 给出两块全等的正三角形纸片(见图 ),要求将其中一块剪拼成一个底面为正三角形的四面体,另一块剪拼成一个上、下底面均为正三角形直三棱柱模型,使它们的表面积都与原三角形的面积相等.请设计一种剪拼方法,分别在图中用虚线标示,并作简要说明.
4.4 设计制作长方体形状的包装纸盒
参考答案1. C 2. D 3. A 4. B 5. B 6. B 7. D 8. 三棱锥
9. 10. 圆锥,三棱柱,长方体 11. 长方体,正方体 12. 13.
14. 展开的方式不同,展开图的周长是不相同的.
图1所示方式展开,
周长为 ;用图2所示方式展开,
周长为 ;
用图 3所示方式展开,
周长为 .
综上,用图1所示方式展开,展开图的周长最小.
15. (1) 右面(2) 面(3) 面(4) 面(5) 后面
16. (1) 拼图存在问题,如图:
(2)12
17. 在正方形的四个角上剪出四个边长为原正方形边长的 的正方形,再沿虚线折叠,即可构成一个缺少上底,而下底为正方形的直四棱柱,而剪下的四个正方形恰好能拼成这个四棱柱的上底,如图所示.
18.四面体:取正三角形各边中点,沿各边中点连线折叠即成四面体(如图).
直三棱柱:在正三角形的三个角上剪出三个全等的,有一组对角为直角,其中夹角为 的相邻两边长为正三角形边长的 的四边形,再沿虚线折叠,即可构成一个缺少上底,下底为正三角形的直三棱柱,其剪下的三个相同的四边形恰好能拼成这个三棱柱的上底(如图 ).
21世纪教育网(www.21cnjy.com)
4.4 课题学习 设计制作长方体形状的包装纸盒
一、选择题
1. 下图中各硬纸片,不可以沿虚线折叠成长方体纸盒的是
A. ①② B. ②③ C. ③④ D. ①④
2. 下列平面图形经过折叠不能围成棱柱的是
A. B. C. D.
3. 下列四个图形中是三棱柱的表面展开图的是
A. B. C. D.
4. 下列四个图形中,是三棱柱的平面展开图的是
A. B. C. D.
5. 图 是下列几何体 的平面展开图.
A. B. C. D.
6. 图①是由白色纸板拼成的立体图形,将它的两个面的外表面涂上颜色,如图②.则下列图形中,是图②的表面展开图的是
A. B. C. D.
7. 下面的四个展开图中,是如图所示的三棱柱纸盒的展开图的是
A. B. C. D.
二、填空题
8. 如图,沿等边三角形三边中点的连线折起,可拼得一个 .
9. 如图,一只蚂蚁从长为 、宽为 ,高是 的长方体纸箱的 点沿纸箱爬到 点,那么它所行的最短路线的长是 .
10. 如图是某些几何体的展开图,请填出这些几何体的名称.
;
;
.
11. 如图所示的两个平面图形分别是两种包装盒的展开图,这两个包装盒的形状分别是 , .
12. 如图,一个长方体的表面展开图中四边形 是正方形,则根据图中数据可得原长方体的体积是 .
13. 如图为一个无盖长方体盒子的展开图(重叠部分不计),根据图中数据,可知该无盖长方体的容积为 .
三、解答题
14. 要制作一个长 、宽 、高 的长方体纸盒,先要在纸板上画出展开图,而展开方式不同,展开图的周长是否相同呢 若不相同,在什么情况下,平面展开图周长最小 请你画出此时它的平面展开图.
15. 如图是一长方体的展开图,每一面内都标注了字母(标字母的面是外表面),根据要求回答问题:
(1)如果 面在多面体的左面,那么 面在哪里
(2) 面和哪个面是相对的面
(3)如果 面在前面,从上面看到的是 面,那么从左面看是哪一面
(4)如果 面在后面,从左面看是 面,那么前面是哪个面
(5)如果 面在右面,从下面看是 面,那么 面在哪里
16. 如图,小华用若干个正方形和长方形准备拼成一个长方体的展开图.拼完后,小华看来看去总觉得所拼图形似乎存在问题.
(1)请你帮小华分析一下拼图是否存在问题:若有多余块,则把图中多余部分涂黑;若还缺少,则直接在原图中补全.
(2)若图中的正方形边长为 ,长方形的长为 ,宽为 ,请直接写出修正后所折叠而成的长方体的容积:
17. 给出一张正方形纸片(见图),要求将其剪拼成一个上、下底面均为正方形的直四棱柱模型,使它的表面积与原正方形的面积相等.请设计一种剪拼方法,在图中用虚线标示,并作简要说明.
18. 给出两块全等的正三角形纸片(见图 ),要求将其中一块剪拼成一个底面为正三角形的四面体,另一块剪拼成一个上、下底面均为正三角形直三棱柱模型,使它们的表面积都与原三角形的面积相等.请设计一种剪拼方法,分别在图中用虚线标示,并作简要说明.
4.4 设计制作长方体形状的包装纸盒
参考答案1. C 2. D 3. A 4. B 5. B 6. B 7. D 8. 三棱锥
9. 10. 圆锥,三棱柱,长方体 11. 长方体,正方体 12. 13.
14. 展开的方式不同,展开图的周长是不相同的.
图1所示方式展开,
周长为 ;用图2所示方式展开,
周长为 ;
用图 3所示方式展开,
周长为 .
综上,用图1所示方式展开,展开图的周长最小.
15. (1) 右面(2) 面(3) 面(4) 面(5) 后面
16. (1) 拼图存在问题,如图:
(2)12
17. 在正方形的四个角上剪出四个边长为原正方形边长的 的正方形,再沿虚线折叠,即可构成一个缺少上底,而下底为正方形的直四棱柱,而剪下的四个正方形恰好能拼成这个四棱柱的上底,如图所示.
18.四面体:取正三角形各边中点,沿各边中点连线折叠即成四面体(如图).
直三棱柱:在正三角形的三个角上剪出三个全等的,有一组对角为直角,其中夹角为 的相邻两边长为正三角形边长的 的四边形,再沿虚线折叠,即可构成一个缺少上底,下底为正三角形的直三棱柱,其剪下的三个相同的四边形恰好能拼成这个三棱柱的上底(如图 ).
21世纪教育网(www.21cnjy.com)
