1.2.4绝对值 课件(共24张PPT)
文档属性
| 名称 | 1.2.4绝对值 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-16 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
1.2.4绝对值
人教版 七年级上册
教学目标
教学目标:
1.理解绝对值的意义,使学生学会求一个数的绝对值.
2.通过观察、比较、归纳得出绝对值的概念,让学生感受数形结合的思想.
重点:理解绝对值的意义,会求一个数的绝对值.
难点:对绝对值概念的理解.
新知导入
像-2和2,5和-5这样,只有符号不同的两个数叫做互为相反数。
1.相反数的概念
与原点的距离相等且分别在原点左右(即关于原点对称).
2.互为相反数的两个数的点在数轴上的位置有什么特点
3.-2,4,-,0,2 022的相反数分别是什么?
2
-2022
-4
0
新知讲解
两辆汽车从同一处O出发,分别向东、西方向行驶了10千米,到达A、B两处.它们的行驶路线相同吗? 行驶的路程分别是多少?
A
B
10
10
O
10
-10
它们的行驶路线不同,A是向东,B是向西.
行驶的路程相等,都是10千米.
思考
新知讲解
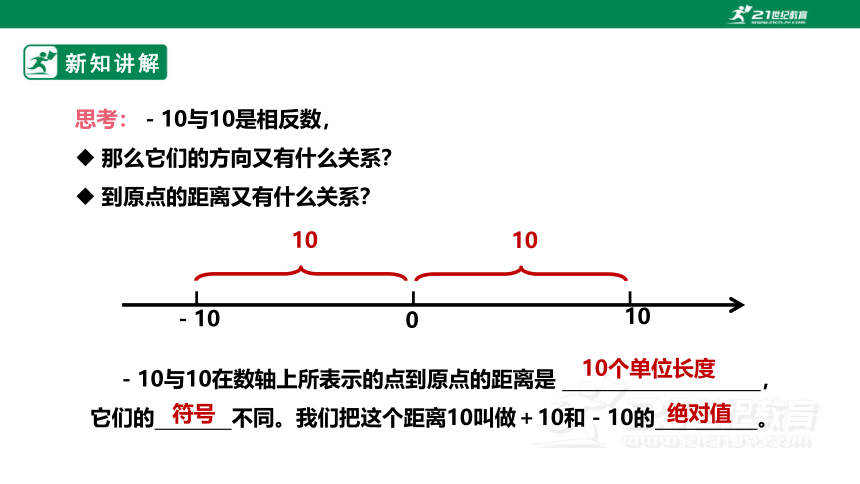
思考:-10与10是相反数,
那么它们的方向又有什么关系?
到原点的距离又有什么关系?
-10
10
0
10
10
-10与10在数轴上所表示的点到原点的距离是 ,它们的 不同。我们把这个距离10叫做+10和-10的 。
10个单位长度
符号
绝对值
新知讲解
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作“|a|”.(这里的数a可以是正数、负数和0).
绝对值:
例如,上面的问题中,在数轴上表示数-10的点和表示数10的点与原点的距离都是10,所以,10与-10的绝对值都是10,即|10|=10,|-10|=10.
-10
10
0
10
10
0到原点的距离是0,所以0的绝对值是0,记做|0|=0
新知讲解
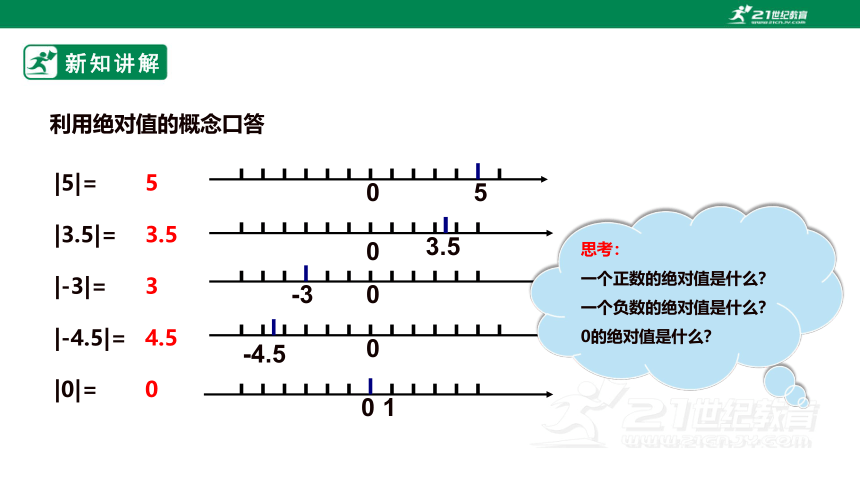
利用绝对值的概念口答
|5|=
|3.5|=
|-3|=
|-4.5|=
|0|=
0
1
0
0
0
0
5
3.5
-3
-4.5
5
3.5
3
4.5
0
思考:
一个正数的绝对值是什么?
一个负数的绝对值是什么?
0的绝对值是什么?
新知讲解
一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0. 即
(1)如果 a>0,那么|a|=___;
(2)如果 a=0,那么|a|=___;
(3)如果 a<0,那么|a|=___.
a
-a
0
非负数,即|a|≥0
由绝对值的定义可知:
一个数a的绝对值是什么数呢?
新知讲解
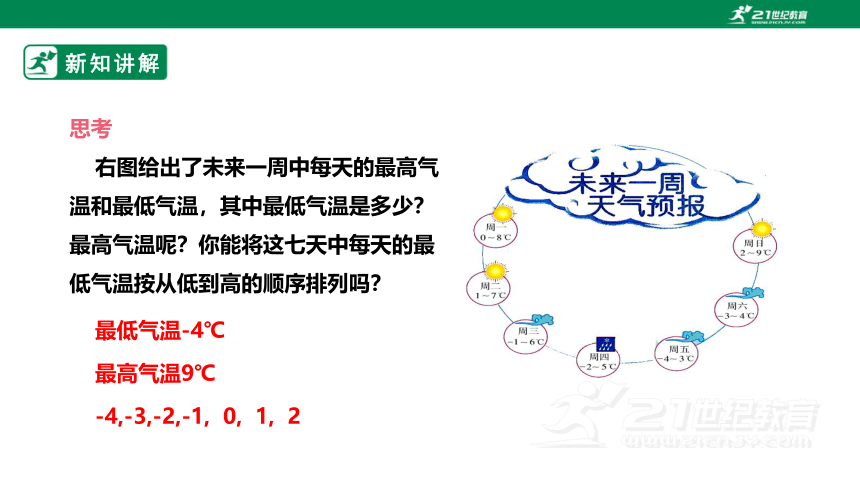
思考
右图给出了未来一周中每天的最高气温和最低气温,其中最低气温是多少?最高气温呢?你能将这七天中每天的最低气温按从低到高的顺序排列吗?
最低气温-4℃
最高气温9℃
-4,-3,-2,-1, 0, 1, 2
新知讲解
你能在数轴上表示出-4, -3, -2, -1, 0, 1, 2吗?
数学中的规定:在数轴上表示有理数,它们从左到右的顺序,就是从小到大的顺序,即左边的数大于右边的数。
观察它们的排列有什么规律
新知讲解
结论:
(1)正数大于0,
(2)两个负数,绝对值大的反而小.
例如,1 > 0,0 > -1,1 > -1,-1 > -2.
负数小于0,
正数大于负数;
问题:
对于正数、0、负数这三类数,它们之间有什么大小关系?两个负数之间如何比较大小?
新知讲解
例、比较下列各数的大小:
(1) -(-1)和-(+2);
解:(1)先化简
-(-1)=1, -(+2)=-2
所以1>-2
即 -(-1) >-(+2);
因为正数大于负数
新知讲解
例、比较下列各数的大小:
(2) 和 ;
(2)这是两个负数比较大小,先求它们的绝对值:
因为 即
所以
新知讲解
例、比较下列各数的大小:
(3) -和|- |
解:先化简-=0.3, |- |=
因为0.3< ,
所以-< |- |
新知讲解
利用法则比较两个数的大小时,可按数的性质符号分类.具体如下:
两数同号 同为正号,绝对值大的数大
同为负号,绝对值大的反而小
两数异号 正数大于负数
一数为0 正数与0,正数大于0
负数与0,负数小于0
比较有理数大小的方法.
方法①:数轴上表示的两个数,右边的总比左 边的大.
方法②:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
课堂练习
(1)|-0.2|=____; (2)|-100|=____;
(3)||=______;(4)|-6.5|=_____;
(5)|y|=____(y<0);(6)||=_____;
(7)-|-7.5|=_____; (8)-|+8|=____;
(9)如果|x|=3,则x= ;
(10)如果|x-3|=0,则|x+2|= .
0.2
100
1.求下列各数的绝对值。
课堂练习
A
D
课堂练习
4. |a|+|b|=|a+b|,则a,b关系是( )
A. a,b的绝对值相等 B. a,b异号
C. a+b的和是非负数 D. a,b同号或其中至少一个为零
D
5.若|a-1|=a-1,则a的取值范围是( )
A.a≥1 B.a≤1 C.a<1 D.a>1
A
课堂练习
(1)绝对值等于0的数是___;
(2)绝对值等于5.25的正数是________;
(3)绝对值等于5.25的负数是______;
(4)|- |的相反数是 ;若|a|=2,则a=___________.
0
5.25
-5.25
6. 填一填:
-
2或-2
课堂练习
7.比较下列各数的大小.
(1) –(-1)和–(+2);
解: 先化简,–(-1)=1,–(+2)=-2
而1>-2,所以–(-1)>–(+2)。
(2) -和-
解:这是两个负数比较大小,先求它们的绝对值。
|-|= ,|-|= =
而< , -> -
课堂练习
8.已知A,B两点在数轴上的位置如图所示,设点A,B,C对应的数分别为a,b,c.
(1)点C在什么位置时,a>c>0
(2)点C在什么位置时,a>c>b
(3)点C在什么位置时,a>b>c
(4)点C在什么位置时,c>a>b
点C在原点和点A之间时
点C在A,B两点之间时
点C在点B的左侧时
点C在点A的右侧时
课堂总结
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作“|a|”.(这里的数a可以是正数、负数和0).
1.绝对值定义:
2.绝对值性质:
一个正数的绝对值是它本身,
一个负数的绝对值是它的相反数,
0的绝对值是0.
3.绝对值的非负性:|a|≥0
4.比较有理数大小的方法:
方法①:数轴上表示的两个数,右边的总比左 边的大.
方法②:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.2.4绝对值
人教版 七年级上册
教学目标
教学目标:
1.理解绝对值的意义,使学生学会求一个数的绝对值.
2.通过观察、比较、归纳得出绝对值的概念,让学生感受数形结合的思想.
重点:理解绝对值的意义,会求一个数的绝对值.
难点:对绝对值概念的理解.
新知导入
像-2和2,5和-5这样,只有符号不同的两个数叫做互为相反数。
1.相反数的概念
与原点的距离相等且分别在原点左右(即关于原点对称).
2.互为相反数的两个数的点在数轴上的位置有什么特点
3.-2,4,-,0,2 022的相反数分别是什么?
2
-2022
-4
0
新知讲解
两辆汽车从同一处O出发,分别向东、西方向行驶了10千米,到达A、B两处.它们的行驶路线相同吗? 行驶的路程分别是多少?
A
B
10
10
O
10
-10
它们的行驶路线不同,A是向东,B是向西.
行驶的路程相等,都是10千米.
思考
新知讲解
思考:-10与10是相反数,
那么它们的方向又有什么关系?
到原点的距离又有什么关系?
-10
10
0
10
10
-10与10在数轴上所表示的点到原点的距离是 ,它们的 不同。我们把这个距离10叫做+10和-10的 。
10个单位长度
符号
绝对值
新知讲解
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作“|a|”.(这里的数a可以是正数、负数和0).
绝对值:
例如,上面的问题中,在数轴上表示数-10的点和表示数10的点与原点的距离都是10,所以,10与-10的绝对值都是10,即|10|=10,|-10|=10.
-10
10
0
10
10
0到原点的距离是0,所以0的绝对值是0,记做|0|=0
新知讲解
利用绝对值的概念口答
|5|=
|3.5|=
|-3|=
|-4.5|=
|0|=
0
1
0
0
0
0
5
3.5
-3
-4.5
5
3.5
3
4.5
0
思考:
一个正数的绝对值是什么?
一个负数的绝对值是什么?
0的绝对值是什么?
新知讲解
一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0. 即
(1)如果 a>0,那么|a|=___;
(2)如果 a=0,那么|a|=___;
(3)如果 a<0,那么|a|=___.
a
-a
0
非负数,即|a|≥0
由绝对值的定义可知:
一个数a的绝对值是什么数呢?
新知讲解
思考
右图给出了未来一周中每天的最高气温和最低气温,其中最低气温是多少?最高气温呢?你能将这七天中每天的最低气温按从低到高的顺序排列吗?
最低气温-4℃
最高气温9℃
-4,-3,-2,-1, 0, 1, 2
新知讲解
你能在数轴上表示出-4, -3, -2, -1, 0, 1, 2吗?
数学中的规定:在数轴上表示有理数,它们从左到右的顺序,就是从小到大的顺序,即左边的数大于右边的数。
观察它们的排列有什么规律
新知讲解
结论:
(1)正数大于0,
(2)两个负数,绝对值大的反而小.
例如,1 > 0,0 > -1,1 > -1,-1 > -2.
负数小于0,
正数大于负数;
问题:
对于正数、0、负数这三类数,它们之间有什么大小关系?两个负数之间如何比较大小?
新知讲解
例、比较下列各数的大小:
(1) -(-1)和-(+2);
解:(1)先化简
-(-1)=1, -(+2)=-2
所以1>-2
即 -(-1) >-(+2);
因为正数大于负数
新知讲解
例、比较下列各数的大小:
(2) 和 ;
(2)这是两个负数比较大小,先求它们的绝对值:
因为 即
所以
新知讲解
例、比较下列各数的大小:
(3) -和|- |
解:先化简-=0.3, |- |=
因为0.3< ,
所以-< |- |
新知讲解
利用法则比较两个数的大小时,可按数的性质符号分类.具体如下:
两数同号 同为正号,绝对值大的数大
同为负号,绝对值大的反而小
两数异号 正数大于负数
一数为0 正数与0,正数大于0
负数与0,负数小于0
比较有理数大小的方法.
方法①:数轴上表示的两个数,右边的总比左 边的大.
方法②:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
课堂练习
(1)|-0.2|=____; (2)|-100|=____;
(3)||=______;(4)|-6.5|=_____;
(5)|y|=____(y<0);(6)||=_____;
(7)-|-7.5|=_____; (8)-|+8|=____;
(9)如果|x|=3,则x= ;
(10)如果|x-3|=0,则|x+2|= .
0.2
100
1.求下列各数的绝对值。
课堂练习
A
D
课堂练习
4. |a|+|b|=|a+b|,则a,b关系是( )
A. a,b的绝对值相等 B. a,b异号
C. a+b的和是非负数 D. a,b同号或其中至少一个为零
D
5.若|a-1|=a-1,则a的取值范围是( )
A.a≥1 B.a≤1 C.a<1 D.a>1
A
课堂练习
(1)绝对值等于0的数是___;
(2)绝对值等于5.25的正数是________;
(3)绝对值等于5.25的负数是______;
(4)|- |的相反数是 ;若|a|=2,则a=___________.
0
5.25
-5.25
6. 填一填:
-
2或-2
课堂练习
7.比较下列各数的大小.
(1) –(-1)和–(+2);
解: 先化简,–(-1)=1,–(+2)=-2
而1>-2,所以–(-1)>–(+2)。
(2) -和-
解:这是两个负数比较大小,先求它们的绝对值。
|-|= ,|-|= =
而< , -> -
课堂练习
8.已知A,B两点在数轴上的位置如图所示,设点A,B,C对应的数分别为a,b,c.
(1)点C在什么位置时,a>c>0
(2)点C在什么位置时,a>c>b
(3)点C在什么位置时,a>b>c
(4)点C在什么位置时,c>a>b
点C在原点和点A之间时
点C在A,B两点之间时
点C在点B的左侧时
点C在点A的右侧时
课堂总结
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作“|a|”.(这里的数a可以是正数、负数和0).
1.绝对值定义:
2.绝对值性质:
一个正数的绝对值是它本身,
一个负数的绝对值是它的相反数,
0的绝对值是0.
3.绝对值的非负性:|a|≥0
4.比较有理数大小的方法:
方法①:数轴上表示的两个数,右边的总比左 边的大.
方法②:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
