4.4 一次函数的应用(3)学案(无答案)
文档属性
| 名称 | 4.4 一次函数的应用(3)学案(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 92.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-16 00:00:00 | ||
图片预览

文档简介
4.4一次函数的应用 (3)
【学习目标】
1.通过观察函数图象,能够从两个一次函数图象中获取信息,理解函数图象交点的实际意义.
2.通过函数图象解决实际问题.
3.通过创设较深层次的问题情境,激发学生参与探索活动,强化数学建模思想,提高学生应用已有知识灵活处理问题的能力.
【学习过程】
一、课前学习
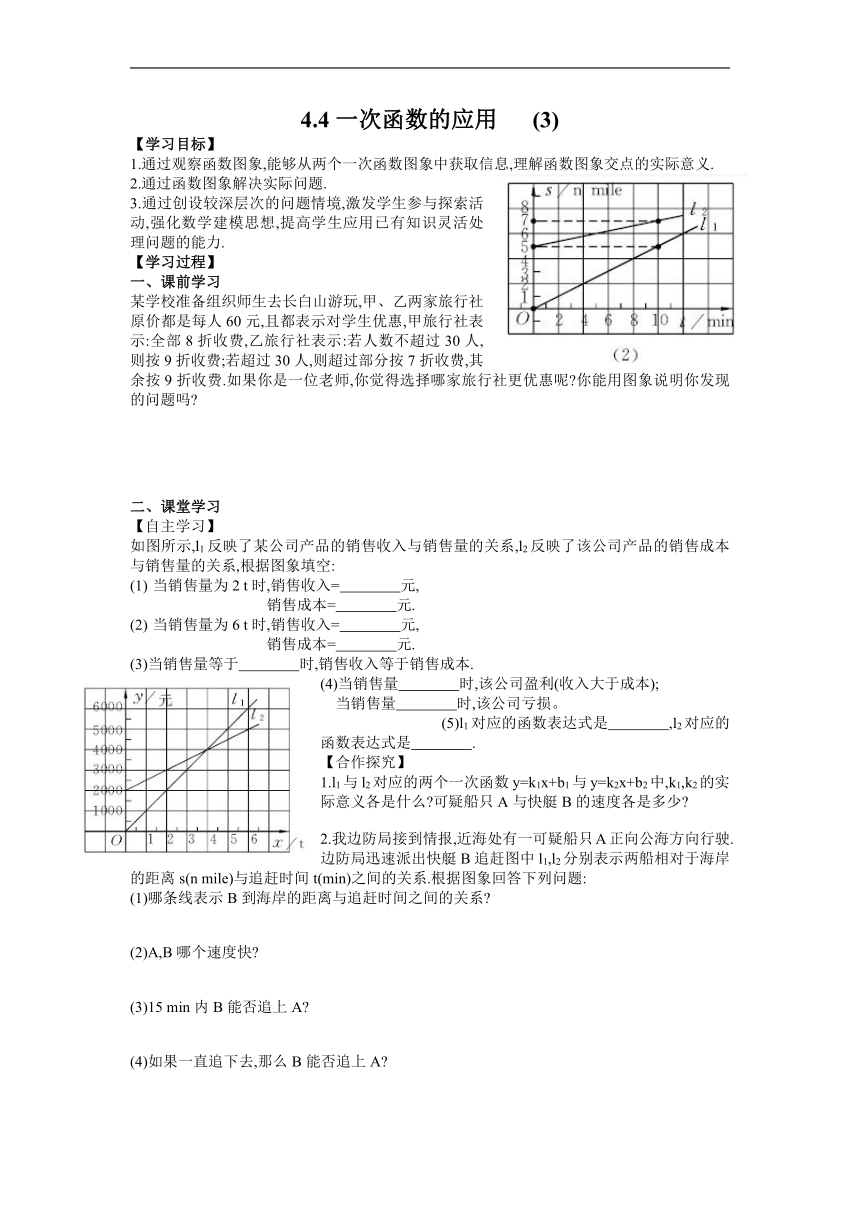
某学校准备组织师生去长白山游玩,甲、乙两家旅行社原价都是每人60元,且都表示对学生优惠,甲旅行社表示:全部8折收费,乙旅行社表示:若人数不超过30人,则按9折收费;若超过30人,则超过部分按7折收费,其余按9折收费.如果你是一位老师,你觉得选择哪家旅行社更优惠呢 你能用图象说明你发现的问题吗
二、课堂学习
【自主学习】
如图所示,l1反映了某公司产品的销售收入与销售量的关系,l2反映了该公司产品的销售成本与销售量的关系,根据图象填空:
当销售量为2 t时,销售收入= 元,
销售成本= 元.
当销售量为6 t时,销售收入= 元,
销售成本= 元.
(3)当销售量等于 时,销售收入等于销售成本.
(4)当销售量 时,该公司盈利(收入大于成本);
当销售量 时,该公司亏损。
(5)l1对应的函数表达式是 ,l2对应的函数表达式是 .
【合作探究】
1.l1与l2对应的两个一次函数y=k1x+b1与y=k2x+b2中,k1,k2的实际意义各是什么 可疑船只A与快艇B的速度各是多少
2.我边防局接到情报,近海处有一可疑船只A正向公海方向行驶.边防局迅速派出快艇B追赶图中l1,l2分别表示两船相对于海岸的距离s(n mile)与追赶时间t(min)之间的关系.根据图象回答下列问题:
哪条线表示B到海岸的距离与追赶时间之间的关系
A,B哪个速度快
(3)15 min内B能否追上A
如果一直追下去,那么B能否追上A
当A逃到离海岸12 n mile的公海时,B将无法对其进行检查.照此速度,B能否在A逃入公海前将其拦截
【练习检测】
1.观察本节第一幅图,回答下列问题:
x=3时,销售收入=________,
销售成本=________;盈利(收入-成本)=________.
2.A,B两地相距80km,甲、乙两人沿同一条路从A地到B地.l1,l2分别表示甲、乙两人离开A地的距离s(km)与时间t(h)之间的关系.根据图象填空:
(1)乙先出发____后,甲才出发;
(2)大约在乙出发____h后,两人相遇,这时
他们离开A地_____km;
(3)甲的速度是____km/h;乙的速度是____km/h.
3.某公司要印制产品宣传材料.甲印刷厂提出:每份材料收1元印制费,另收1500元制版费;乙印刷厂提出:每份材料收2.5元印制费,不收制版费.
(1)分别写出两印刷厂的收费y(元)与印制数量x(份)之间的关系式;
(2)在同一直角坐标系内画出它们的图象;
(3)根据图象回答下列问题:
印制800份宣传材料时,选择哪家印刷厂比较合算?该公司拟拿出3000元用于印制宣传材料,找哪家印刷厂印制宣传材料能多一些?
三、课后巩固
1.如图所示,OA,BA分别表示甲、乙两名学生运动的一次函数图象,图中s和t分别表示运动路程和时间,根据图象求快者的速度比慢者的速度每秒快 ( )
A.2.5 m B.2 m C.1.5 m D.1 m
小明骑自行车从A地去B地,一段时间后小刚骑摩托车也从A地出发追赶小明,两人走的路程s(千米)与小明骑行时间t(时)的关系如图所示.
(1) 表示小明行驶的路程与时间的关系(填“l1”或“l2”);
(2)小刚比小明晚出发 小时;
(3)v小刚= ,v小明= ;
(4)小刚出发 小时后追上小明.
某单位急需用车,但又不准备买车,所以他们准备和一个体车主或一国有出租车公司中的一家签订月租车合同,设汽车每月行驶x km,应付给个体车主的月租费是y1元,应付给国有出租车公司的月租费是y2元,y1,y2与x之间的函数关系图象如下图所示.
根据图象回答下列问题:
每月行驶的路程在什么范围内时,租国有公司的车合算
(2)每月行驶的路程等于多少时,租两家车的费用相同
(3)如果这个单位估计每月行驶的路程为2300 km,那么这个单位租哪家的车合算
四 课后反思 .
【学习目标】
1.通过观察函数图象,能够从两个一次函数图象中获取信息,理解函数图象交点的实际意义.
2.通过函数图象解决实际问题.
3.通过创设较深层次的问题情境,激发学生参与探索活动,强化数学建模思想,提高学生应用已有知识灵活处理问题的能力.
【学习过程】
一、课前学习
某学校准备组织师生去长白山游玩,甲、乙两家旅行社原价都是每人60元,且都表示对学生优惠,甲旅行社表示:全部8折收费,乙旅行社表示:若人数不超过30人,则按9折收费;若超过30人,则超过部分按7折收费,其余按9折收费.如果你是一位老师,你觉得选择哪家旅行社更优惠呢 你能用图象说明你发现的问题吗
二、课堂学习
【自主学习】
如图所示,l1反映了某公司产品的销售收入与销售量的关系,l2反映了该公司产品的销售成本与销售量的关系,根据图象填空:
当销售量为2 t时,销售收入= 元,
销售成本= 元.
当销售量为6 t时,销售收入= 元,
销售成本= 元.
(3)当销售量等于 时,销售收入等于销售成本.
(4)当销售量 时,该公司盈利(收入大于成本);
当销售量 时,该公司亏损。
(5)l1对应的函数表达式是 ,l2对应的函数表达式是 .
【合作探究】
1.l1与l2对应的两个一次函数y=k1x+b1与y=k2x+b2中,k1,k2的实际意义各是什么 可疑船只A与快艇B的速度各是多少
2.我边防局接到情报,近海处有一可疑船只A正向公海方向行驶.边防局迅速派出快艇B追赶图中l1,l2分别表示两船相对于海岸的距离s(n mile)与追赶时间t(min)之间的关系.根据图象回答下列问题:
哪条线表示B到海岸的距离与追赶时间之间的关系
A,B哪个速度快
(3)15 min内B能否追上A
如果一直追下去,那么B能否追上A
当A逃到离海岸12 n mile的公海时,B将无法对其进行检查.照此速度,B能否在A逃入公海前将其拦截
【练习检测】
1.观察本节第一幅图,回答下列问题:
x=3时,销售收入=________,
销售成本=________;盈利(收入-成本)=________.
2.A,B两地相距80km,甲、乙两人沿同一条路从A地到B地.l1,l2分别表示甲、乙两人离开A地的距离s(km)与时间t(h)之间的关系.根据图象填空:
(1)乙先出发____后,甲才出发;
(2)大约在乙出发____h后,两人相遇,这时
他们离开A地_____km;
(3)甲的速度是____km/h;乙的速度是____km/h.
3.某公司要印制产品宣传材料.甲印刷厂提出:每份材料收1元印制费,另收1500元制版费;乙印刷厂提出:每份材料收2.5元印制费,不收制版费.
(1)分别写出两印刷厂的收费y(元)与印制数量x(份)之间的关系式;
(2)在同一直角坐标系内画出它们的图象;
(3)根据图象回答下列问题:
印制800份宣传材料时,选择哪家印刷厂比较合算?该公司拟拿出3000元用于印制宣传材料,找哪家印刷厂印制宣传材料能多一些?
三、课后巩固
1.如图所示,OA,BA分别表示甲、乙两名学生运动的一次函数图象,图中s和t分别表示运动路程和时间,根据图象求快者的速度比慢者的速度每秒快 ( )
A.2.5 m B.2 m C.1.5 m D.1 m
小明骑自行车从A地去B地,一段时间后小刚骑摩托车也从A地出发追赶小明,两人走的路程s(千米)与小明骑行时间t(时)的关系如图所示.
(1) 表示小明行驶的路程与时间的关系(填“l1”或“l2”);
(2)小刚比小明晚出发 小时;
(3)v小刚= ,v小明= ;
(4)小刚出发 小时后追上小明.
某单位急需用车,但又不准备买车,所以他们准备和一个体车主或一国有出租车公司中的一家签订月租车合同,设汽车每月行驶x km,应付给个体车主的月租费是y1元,应付给国有出租车公司的月租费是y2元,y1,y2与x之间的函数关系图象如下图所示.
根据图象回答下列问题:
每月行驶的路程在什么范围内时,租国有公司的车合算
(2)每月行驶的路程等于多少时,租两家车的费用相同
(3)如果这个单位估计每月行驶的路程为2300 km,那么这个单位租哪家的车合算
四 课后反思 .
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
