4.2 一次函数与正比例函数 学案(无答案)
文档属性
| 名称 | 4.2 一次函数与正比例函数 学案(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 108.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-16 00:00:00 | ||
图片预览

文档简介
一次函数与正比例函数
【知识要点】
1.函数: 一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么就称y是x的函数。其中,x是自变量,y是因变量。
2.函数关系三种表示方法:(1)关系式法;(2)列表法;(3)图象法.
3.一次函数:通常可以表示为y=kx+b的形式,其中k、b是常数,k≠0.
特别地,当b=0时,一次函数y=kx(常数k≠0)也叫正比例函数.
正比例函数也是一次函数,它是一次函数的特例.
【例题精讲】
例1:下列各曲线中不能表示y是x函数的是( )
A.B. C.D.
例2:已知函数,则自变量x的取值范围是( )
A.x>2 B.x≠﹣3 C.x>3且x≠﹣2 D.x≥﹣3且x≠2
例3:下列函数中,是一次函数的有( )
(1)y=2x (2)y=x﹣1 (3)y= (4)y=2﹣3x (5)y=x2﹣1.
A.4个 B.3个 C.2个 D.1个
例4:在y=(k+1)x+k2﹣1中,若y是x的正比例函数,则k值为 。
例5:已知y﹣1与x+2成正比例,且x=﹣1时,y=3.
(1)求y与x之间的函数关系式;
(2)若点(2m+1,3)是该函数图象上的一点,求m的值.
例6:某桶装水销售部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元,现在每桶水的销售价格为8元,如果用x(单位:桶)表示每天的销售数量,用y(元)表示每天的利润(利润=总销售额﹣固定成本﹣售出水的成本).
(1)试写出y与x的函数关系式.
(2)若现在固定成本增加了5%,每桶水的进价增加了1元,求此时y与x的函数关系式.
【课堂巩固】
一.选择题。
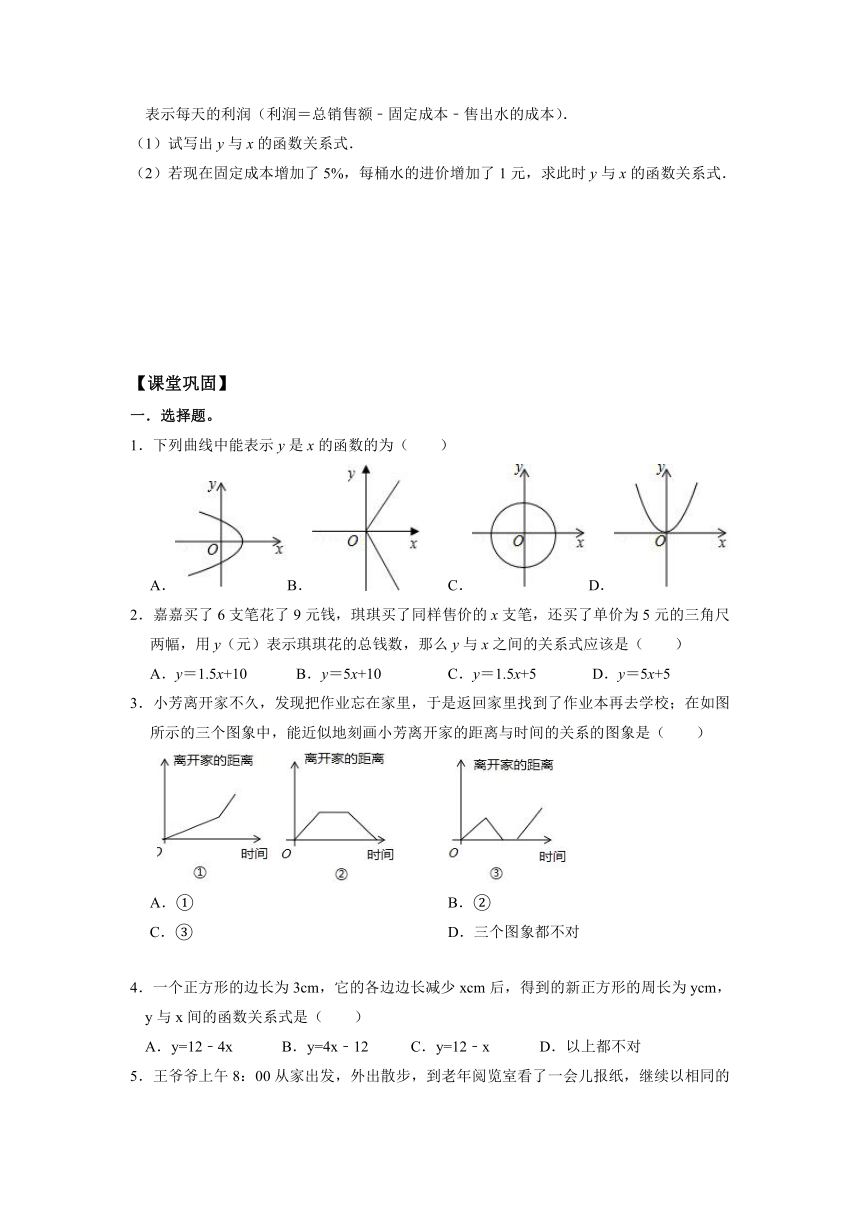
1.下列曲线中能表示y是x的函数的为( )
A.B. C.D.
2.嘉嘉买了6支笔花了9元钱,琪琪买了同样售价的x支笔,还买了单价为5元的三角尺两幅,用y(元)表示琪琪花的总钱数,那么y与x之间的关系式应该是( )
A.y=1.5x+10 B.y=5x+10 C.y=1.5x+5 D.y=5x+5
3.小芳离开家不久,发现把作业忘在家里,于是返回家里找到了作业本再去学校;在如图所示的三个图象中,能近似地刻画小芳离开家的距离与时间的关系的图象是( )
A.① B.②
C.③ D.三个图象都不对
4.一个正方形的边长为3cm,它的各边边长减少xcm后,得到的新正方形的周长为ycm,
y与x间的函数关系式是( )
A.y=12﹣4x B.y=4x﹣12 C.y=12﹣x D.以上都不对
5.王爷爷上午8:00从家出发,外出散步,到老年阅览室看了一会儿报纸,继续以相同的速度散步一段时间,然后回家.如图描述了王爷爷在散步过程中离家的路程s(米)与所用时间t(分)之间的函数关系,则下列信息错误的是( )
A.王爷爷看报纸用了20分钟
B.王爷爷一共走了1600米
C.王爷爷回家的速度是80米/分
D.上午8:32王爷爷在离家800米处
6.下列关系式中,y是x的一次函数的有( )
①y=2x﹣3; ②y=﹣; ③y=+x; ④y=10﹣1﹣25x; ⑤y=+1.
A.1个 B.2个 C.3个 D.4个
7.已知是正比例函数,则m的值是( )
A.8 B.4 C.±3 D.3
8.直线y=3x+b经过点(m,n),且n﹣3m=8,则b的值是( )
A.﹣4 B.4 C.﹣8 D.8
9.已知y与(x﹣2)成正比例,当x=1时,y=﹣2.则当x=3时,y的值为( )
A.2 B.﹣2 C.3 D.﹣3
10.如图,下列图形都是由大小一样的正方形按一定的规律组成的,其中,第①个图形中黑色正方形有4个,第②个图形中黑色正方形有7个,第③个图形中黑色正方形有10个,……,按此规律,则第⑧个图形中黑色正方形的个数为( )
A.26 B.20 C.21 D.25
11.如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )
A. B.
C. D.
二.填空题。
12.函数y=+的自变量x的取值范围是 。
13.甲骑自行车,乙乘公交车,从同一地点出发沿相同路线
前往某校参加绘画比赛,图中l甲、l乙分别表示甲、乙两人
前往目的地所行使的路程s(千米)随时间t(分)变化的
函数图象,则每分钟乙比甲多行驶 千米.
14.某地市话的收费标准为:
(1)通话时间在3分钟以内(包括3分钟)话费1.5元;
(2)通话时间超过3分钟时,超过部分的话费按每分钟0.25元计算.
在一次通话中,那么话费y(元)与通话时间x(分钟)之间的关系式为 .
15.已知一个等腰三角形的周长是40cm,那么腰长y (cm)是底边长x (cm)的函数解析式是 ;其中自变量x 的取值范围是 .
三.解答题。
16.为了了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表
汽车行驶时间x(h) 0 1 2 3 …
油箱剩余油量y 100 94 88 82 …
(1)根据上表的数据,请写出y与x的之间的关系式: ;
(2)如果汽车油箱中剩余油量为46L,则汽车行驶了多少小时?
(3)如果该种汽车油箱只装了36L汽油,汽车以100km/h的速度在一条全长700公里的高速公路上匀速行驶,请问它在中途不加油的情况下能从高速公路起点开到高速公路终点吗?为什么?
17.已知函数y=(m+1)x2﹣|m|+n+4.
(1)当m,n为何值时,此函数是一次函数?
(2)当m,n为何值时,此函数是正比例函数?
18.已知y=y1+y2,y1与x成正比例,y2与x﹣1成正比例,且x=3时,y=4;x=1时,y=2,求y与x之间的函数关系式.
19.甲乙两个仓库要向A、B两地运送水泥,已知甲仓库可调出100吨水泥,乙仓库可调出80吨水泥,A地需70吨水泥,B地需110吨水泥,两仓库到A,B两地的路程和运费如下表(表中运费栏“元/(吨 千米)”表示每吨水泥运送1千米所需人民币),设甲仓库运往A地水泥x吨,求总运费y(元)关于x(吨)的函数关系式.
路程/千米 运费(元/吨 千米)
甲仓库 乙仓库 甲仓库 乙仓库
A地 20 15 12 12
B地 25 20 10 8
【知识要点】
1.函数: 一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么就称y是x的函数。其中,x是自变量,y是因变量。
2.函数关系三种表示方法:(1)关系式法;(2)列表法;(3)图象法.
3.一次函数:通常可以表示为y=kx+b的形式,其中k、b是常数,k≠0.
特别地,当b=0时,一次函数y=kx(常数k≠0)也叫正比例函数.
正比例函数也是一次函数,它是一次函数的特例.
【例题精讲】
例1:下列各曲线中不能表示y是x函数的是( )
A.B. C.D.
例2:已知函数,则自变量x的取值范围是( )
A.x>2 B.x≠﹣3 C.x>3且x≠﹣2 D.x≥﹣3且x≠2
例3:下列函数中,是一次函数的有( )
(1)y=2x (2)y=x﹣1 (3)y= (4)y=2﹣3x (5)y=x2﹣1.
A.4个 B.3个 C.2个 D.1个
例4:在y=(k+1)x+k2﹣1中,若y是x的正比例函数,则k值为 。
例5:已知y﹣1与x+2成正比例,且x=﹣1时,y=3.
(1)求y与x之间的函数关系式;
(2)若点(2m+1,3)是该函数图象上的一点,求m的值.
例6:某桶装水销售部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元,现在每桶水的销售价格为8元,如果用x(单位:桶)表示每天的销售数量,用y(元)表示每天的利润(利润=总销售额﹣固定成本﹣售出水的成本).
(1)试写出y与x的函数关系式.
(2)若现在固定成本增加了5%,每桶水的进价增加了1元,求此时y与x的函数关系式.
【课堂巩固】
一.选择题。
1.下列曲线中能表示y是x的函数的为( )
A.B. C.D.
2.嘉嘉买了6支笔花了9元钱,琪琪买了同样售价的x支笔,还买了单价为5元的三角尺两幅,用y(元)表示琪琪花的总钱数,那么y与x之间的关系式应该是( )
A.y=1.5x+10 B.y=5x+10 C.y=1.5x+5 D.y=5x+5
3.小芳离开家不久,发现把作业忘在家里,于是返回家里找到了作业本再去学校;在如图所示的三个图象中,能近似地刻画小芳离开家的距离与时间的关系的图象是( )
A.① B.②
C.③ D.三个图象都不对
4.一个正方形的边长为3cm,它的各边边长减少xcm后,得到的新正方形的周长为ycm,
y与x间的函数关系式是( )
A.y=12﹣4x B.y=4x﹣12 C.y=12﹣x D.以上都不对
5.王爷爷上午8:00从家出发,外出散步,到老年阅览室看了一会儿报纸,继续以相同的速度散步一段时间,然后回家.如图描述了王爷爷在散步过程中离家的路程s(米)与所用时间t(分)之间的函数关系,则下列信息错误的是( )
A.王爷爷看报纸用了20分钟
B.王爷爷一共走了1600米
C.王爷爷回家的速度是80米/分
D.上午8:32王爷爷在离家800米处
6.下列关系式中,y是x的一次函数的有( )
①y=2x﹣3; ②y=﹣; ③y=+x; ④y=10﹣1﹣25x; ⑤y=+1.
A.1个 B.2个 C.3个 D.4个
7.已知是正比例函数,则m的值是( )
A.8 B.4 C.±3 D.3
8.直线y=3x+b经过点(m,n),且n﹣3m=8,则b的值是( )
A.﹣4 B.4 C.﹣8 D.8
9.已知y与(x﹣2)成正比例,当x=1时,y=﹣2.则当x=3时,y的值为( )
A.2 B.﹣2 C.3 D.﹣3
10.如图,下列图形都是由大小一样的正方形按一定的规律组成的,其中,第①个图形中黑色正方形有4个,第②个图形中黑色正方形有7个,第③个图形中黑色正方形有10个,……,按此规律,则第⑧个图形中黑色正方形的个数为( )
A.26 B.20 C.21 D.25
11.如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )
A. B.
C. D.
二.填空题。
12.函数y=+的自变量x的取值范围是 。
13.甲骑自行车,乙乘公交车,从同一地点出发沿相同路线
前往某校参加绘画比赛,图中l甲、l乙分别表示甲、乙两人
前往目的地所行使的路程s(千米)随时间t(分)变化的
函数图象,则每分钟乙比甲多行驶 千米.
14.某地市话的收费标准为:
(1)通话时间在3分钟以内(包括3分钟)话费1.5元;
(2)通话时间超过3分钟时,超过部分的话费按每分钟0.25元计算.
在一次通话中,那么话费y(元)与通话时间x(分钟)之间的关系式为 .
15.已知一个等腰三角形的周长是40cm,那么腰长y (cm)是底边长x (cm)的函数解析式是 ;其中自变量x 的取值范围是 .
三.解答题。
16.为了了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表
汽车行驶时间x(h) 0 1 2 3 …
油箱剩余油量y 100 94 88 82 …
(1)根据上表的数据,请写出y与x的之间的关系式: ;
(2)如果汽车油箱中剩余油量为46L,则汽车行驶了多少小时?
(3)如果该种汽车油箱只装了36L汽油,汽车以100km/h的速度在一条全长700公里的高速公路上匀速行驶,请问它在中途不加油的情况下能从高速公路起点开到高速公路终点吗?为什么?
17.已知函数y=(m+1)x2﹣|m|+n+4.
(1)当m,n为何值时,此函数是一次函数?
(2)当m,n为何值时,此函数是正比例函数?
18.已知y=y1+y2,y1与x成正比例,y2与x﹣1成正比例,且x=3时,y=4;x=1时,y=2,求y与x之间的函数关系式.
19.甲乙两个仓库要向A、B两地运送水泥,已知甲仓库可调出100吨水泥,乙仓库可调出80吨水泥,A地需70吨水泥,B地需110吨水泥,两仓库到A,B两地的路程和运费如下表(表中运费栏“元/(吨 千米)”表示每吨水泥运送1千米所需人民币),设甲仓库运往A地水泥x吨,求总运费y(元)关于x(吨)的函数关系式.
路程/千米 运费(元/吨 千米)
甲仓库 乙仓库 甲仓库 乙仓库
A地 20 15 12 12
B地 25 20 10 8
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
