13.3.1等腰三角形的判定 课件(共23张PPT)
文档属性
| 名称 | 13.3.1等腰三角形的判定 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-18 13:56:35 | ||
图片预览






文档简介
(共23张PPT)
13.3.1等腰三角形的判定
人教版八年级上册
知识回顾
等腰三角形的性质1:等腰三角形的两个底角相等(简写成“等边对等角”).
等腰三角形的性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简写成“三线合一”).
等腰三角形有哪些性质?
教学目标
1.掌握等腰三角形的判定方法,并运用其进行证明和计算.
2.掌握等腰三角形相关定理的运用,例如“等边对等角”和“等角对等边”
新知导入
我们知道,等腰三角形的两个底角相等,也就是如果一个三角形有两条边相等,那么它们所对的角相等. 反过来,如果一个三角形有两个角相等,那么它们所对的边有什么关系?
猜想:如果一个三角形有两个角相等,那么它们所对的边相等
答:相等
接下来就要验证猜想
新知探究
等腰三角形的判定
知识点 1
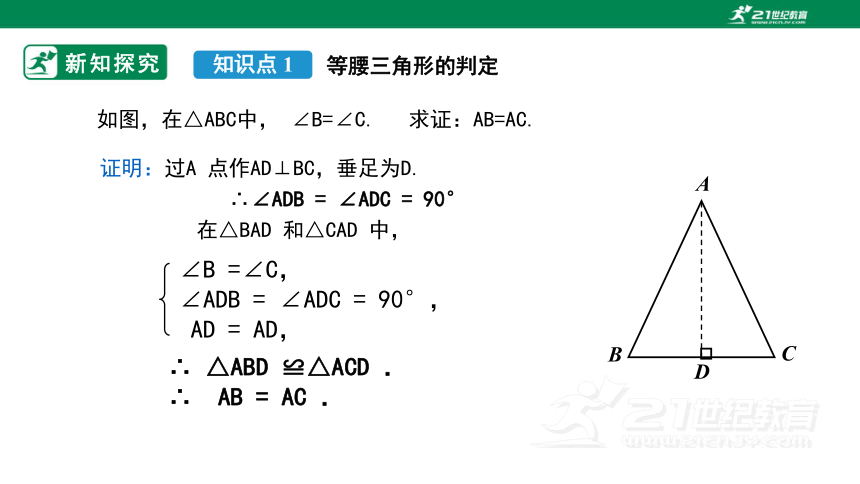
如图,在△ABC中, ∠B=∠C. 求证:AB=AC.
A
B
C
D
证明:过A 点作AD⊥BC,垂足为D.
∴∠ADB = ∠ADC = 90°
在△BAD 和△CAD 中,
∠B =∠C,
∠ADB = ∠ADC = 90°,
AD = AD,
∴ △ABD ≌△ACD .
∴ AB = AC .
新知探究
等腰三角形的判定:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
几何语言:如图,在△ABC中,
∵∠B=∠C,(已知)
∴AB=AC.( )
即△ABC为等腰三角形.
A
B
C
注意:应用“等角对等边”的前提条件是在同一个三角形中.
等角对等边
新知典例
例1 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
A
B
C
D
E
1
2
已知: 如图,∠CAE是△ABC的外角,∠1=∠2,AD∥BC.
求证:AB=AC.
证明:∵AD∥BC,
∴∠1=∠B(两直线平行,同位角相等),
∠2=∠C(两直线平行,内错角相等).
又∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等角对等边).
课堂练习
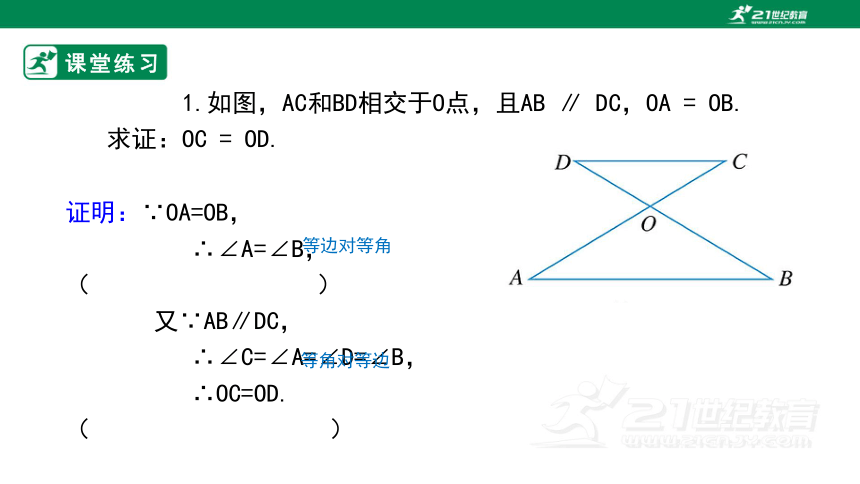
1.如图,AC和BD相交于O点,且AB ∥ DC,OA = OB. 求证:OC = OD.
证明:∵OA=OB,
∴∠A=∠B,( )
又∵AB∥DC,
∴∠C=∠A=∠D=∠B,
∴OC=OD. ( )
等边对等角
等角对等边
新知探究
由平行及角平分线识别等腰三角形
知识点 2
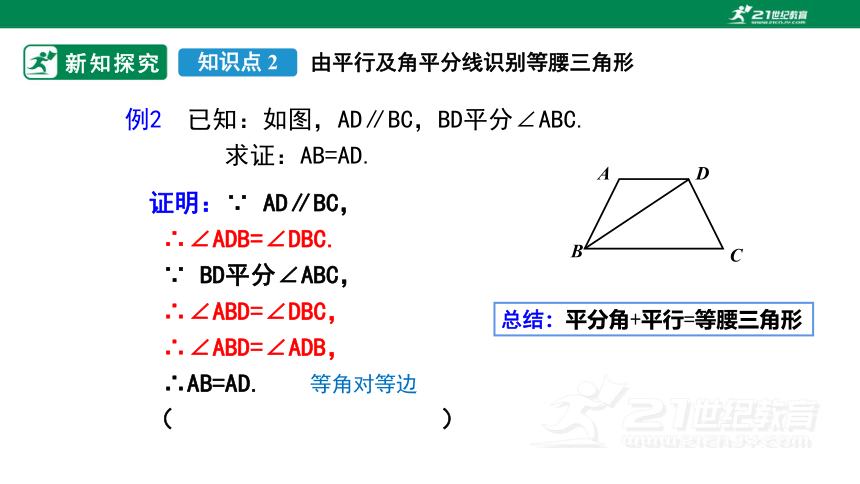
例2 已知:如图,AD∥BC,BD平分∠ABC.
求证:AB=AD.
B
A
D
C
证明:∵ AD∥BC,
∴∠ADB=∠DBC.
∵ BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD.( )
总结:平分角+平行=等腰三角形
等角对等边
课堂练习
如图,把一张长方形的纸沿着对角线折叠,重合部分是一个等腰三角形吗?为什么?
B
C
A
D
E
解:是
由折叠可知,∠EBD=∠CBD.
∵AD∥BC,∴∠EDB=∠CBD,
∴∠EDB=∠EBD,
∴BE=DE,( )
即△EBD是等腰三角形.
等角对等边
注意:折叠也是构成角平分线的一种形式
课堂小结
“角平分线+平行线构成等腰三角形”模型及应用
图2
图3
图4
1
2
1
2
1
2
图1 已知AC∥BD,BC平分∠ABD.等腰三角形为 .
图2 已知AD∥BC,AD平分∠CAE.等腰三角形为 .
△ABC
△ABC
图3 已知ED∥BC,BD平分∠ABC.等腰三角形为 .
△BED
图4 已知ED∥BC,BF平分∠ABC,CF平分∠ACB.等腰三角形为 .
△BDF和△CEF
新知探究
例3 已知等腰三角形底边长为a,底边上的高的长为h,求作等腰△ABC.使底边BC=a,底边上的高为h.
a
h
作法:
1.作线段AB=a.
2.作线段AB的垂直平分线MN,交AB 于点D.
3.在MN上取一点C,使DC=h.
4.连接AC,BC,则△ABC即为所求.
A
B
C
M
N
D
利用尺规作图作等腰三角形
知识点 3
课堂练习
已知等腰三角形的底边长为a,顶角的平分线长为b,求作这个等腰三角形.
(尺规作图,保留作图痕迹,不用证明)
解:
作图:
①画射线AE,在射线上截取AB=a,
②作AB的垂直平分线,垂足为O,再截取CO=b,
③再连接AC、CB,△ABC即为所求.
课堂小测
1.如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:
①△BDF和△CEF都是等腰三角形;
②DE=BD+CE;
③△ADE的周长等于AB与AC的和;
④BF=CF.
其中正确的有( )
A.①②③ B.①②③④ C.①② D.①
A
课堂小测
2.如图,在直角三角形ABC中,∠ACB=90°,∠B=36°,点D、E在AB上,如果BC=BD,∠CED=∠CDE,那么图中的等腰三角形共有( )个.
A.3个 B.4个 C.5个 D.6个
解:∵∠ACB=90°,∠B=36°,
∴∠A=54°,
∵BC=BD,
∴∠CDB=∠DCB=72°,
∴∠ECB=36°,∠ACE=54°,
∴CE=BE,AE=CE,
∴△BCD,△CDE,△CEB,△ACE都是等腰三角形,
B
课堂小测
3.如图,将一张长方形纸片ABCD按图中方式进行折叠,若AE=3,AB=4,BE=5,则重叠部分的面积是 .
10
解:∵长方形纸片ABCD按图中那样折叠
∴∠1=∠2,
而∠1=∠3,
∴∠2=∠3,
∴ED=EB,
又∵AE=3,AB=4,BE=5,
∴DE=5,
∴重叠部分△BDE的面积=
DE×AB=
×5×4=10.
课堂小测
4.在△ABC中,∠BAC=90°,∠C=30°.用无刻度的直尺和圆规在BC边上找一点D,使△ACD为等腰三角形.下列作法正确的有 个.
3
课堂小测
5.如图:△ABC的边AB的延长线上有一个点D,过点D作DF⊥AC于F,交BC于E,且BD=BE,求证:△ABC为等腰三角形.
证明:∵DF⊥AC,
∴∠DFA=∠EFC=90°.
∴∠A=∠DFA﹣∠D,∠C=∠EFC﹣∠CEF,
∵BD=BE,
∴∠BED=∠D.
∵∠BED=∠CEF,
∴∠D=∠CEF.
∴∠A=∠C.
∴△ABC为等腰三角形.
脑筋急转
6.如图,在△ABC中,∠A=60°.BE,CF交于点P,且分别平分∠ABC,∠ACB.
(1)求∠BPC的度数;
(2)连接EF,求证:△EFP是等腰三角形.
(1)解:∵∠A=60°,
∴∠ABC+∠ACB=180°﹣∠A=120°,
∵BE平分∠ABC,CF平分∠ACB,
∴∠ABE=∠CBE=
ABC,
∴∠CBE+∠BCF=
∠ABC+
ACB=
=60°,
∴∠BPC=180°﹣(∠CBE+∠BCF)=180°﹣60°=120°;
脑筋急转
6.如图,在△ABC中,∠A=60°.BE,CF交于点P,且分别平分∠ABC,∠ACB.
(1)求∠BPC的度数;
(2)连接EF,求证:△EFP是等腰三角形.
在△FBP和△QBP中,
∴△FBP≌△QBP(SAS),
∴FP=QP,∠BFP=∠BQP,
∵∠A=60°,∠FPE=∠BPC=120°,
∴∠AFP+∠AEP=360°﹣60°﹣120°=180°,
∴∠BFP+∠CEP=180°,
∵∠CQP+∠BQP=180°,
∴∠CEP=∠CQP,
在△CQP和△CEP中,
∴△CQP≌△CEP(AAS),
∴EF=QP,
∵FP=EP,
∴△EFP是等腰三角形.
证明:在BC上截取BQ=BF,连接PQ,
课堂总结
等腰
三角形
判定
综合应用
如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)
将等腰三角形的性质和判定综合应用在解决实际问题中
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
13.3.1等腰三角形的判定
人教版八年级上册
知识回顾
等腰三角形的性质1:等腰三角形的两个底角相等(简写成“等边对等角”).
等腰三角形的性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简写成“三线合一”).
等腰三角形有哪些性质?
教学目标
1.掌握等腰三角形的判定方法,并运用其进行证明和计算.
2.掌握等腰三角形相关定理的运用,例如“等边对等角”和“等角对等边”
新知导入
我们知道,等腰三角形的两个底角相等,也就是如果一个三角形有两条边相等,那么它们所对的角相等. 反过来,如果一个三角形有两个角相等,那么它们所对的边有什么关系?
猜想:如果一个三角形有两个角相等,那么它们所对的边相等
答:相等
接下来就要验证猜想
新知探究
等腰三角形的判定
知识点 1
如图,在△ABC中, ∠B=∠C. 求证:AB=AC.
A
B
C
D
证明:过A 点作AD⊥BC,垂足为D.
∴∠ADB = ∠ADC = 90°
在△BAD 和△CAD 中,
∠B =∠C,
∠ADB = ∠ADC = 90°,
AD = AD,
∴ △ABD ≌△ACD .
∴ AB = AC .
新知探究
等腰三角形的判定:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
几何语言:如图,在△ABC中,
∵∠B=∠C,(已知)
∴AB=AC.( )
即△ABC为等腰三角形.
A
B
C
注意:应用“等角对等边”的前提条件是在同一个三角形中.
等角对等边
新知典例
例1 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
A
B
C
D
E
1
2
已知: 如图,∠CAE是△ABC的外角,∠1=∠2,AD∥BC.
求证:AB=AC.
证明:∵AD∥BC,
∴∠1=∠B(两直线平行,同位角相等),
∠2=∠C(两直线平行,内错角相等).
又∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等角对等边).
课堂练习
1.如图,AC和BD相交于O点,且AB ∥ DC,OA = OB. 求证:OC = OD.
证明:∵OA=OB,
∴∠A=∠B,( )
又∵AB∥DC,
∴∠C=∠A=∠D=∠B,
∴OC=OD. ( )
等边对等角
等角对等边
新知探究
由平行及角平分线识别等腰三角形
知识点 2
例2 已知:如图,AD∥BC,BD平分∠ABC.
求证:AB=AD.
B
A
D
C
证明:∵ AD∥BC,
∴∠ADB=∠DBC.
∵ BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD.( )
总结:平分角+平行=等腰三角形
等角对等边
课堂练习
如图,把一张长方形的纸沿着对角线折叠,重合部分是一个等腰三角形吗?为什么?
B
C
A
D
E
解:是
由折叠可知,∠EBD=∠CBD.
∵AD∥BC,∴∠EDB=∠CBD,
∴∠EDB=∠EBD,
∴BE=DE,( )
即△EBD是等腰三角形.
等角对等边
注意:折叠也是构成角平分线的一种形式
课堂小结
“角平分线+平行线构成等腰三角形”模型及应用
图2
图3
图4
1
2
1
2
1
2
图1 已知AC∥BD,BC平分∠ABD.等腰三角形为 .
图2 已知AD∥BC,AD平分∠CAE.等腰三角形为 .
△ABC
△ABC
图3 已知ED∥BC,BD平分∠ABC.等腰三角形为 .
△BED
图4 已知ED∥BC,BF平分∠ABC,CF平分∠ACB.等腰三角形为 .
△BDF和△CEF
新知探究
例3 已知等腰三角形底边长为a,底边上的高的长为h,求作等腰△ABC.使底边BC=a,底边上的高为h.
a
h
作法:
1.作线段AB=a.
2.作线段AB的垂直平分线MN,交AB 于点D.
3.在MN上取一点C,使DC=h.
4.连接AC,BC,则△ABC即为所求.
A
B
C
M
N
D
利用尺规作图作等腰三角形
知识点 3
课堂练习
已知等腰三角形的底边长为a,顶角的平分线长为b,求作这个等腰三角形.
(尺规作图,保留作图痕迹,不用证明)
解:
作图:
①画射线AE,在射线上截取AB=a,
②作AB的垂直平分线,垂足为O,再截取CO=b,
③再连接AC、CB,△ABC即为所求.
课堂小测
1.如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:
①△BDF和△CEF都是等腰三角形;
②DE=BD+CE;
③△ADE的周长等于AB与AC的和;
④BF=CF.
其中正确的有( )
A.①②③ B.①②③④ C.①② D.①
A
课堂小测
2.如图,在直角三角形ABC中,∠ACB=90°,∠B=36°,点D、E在AB上,如果BC=BD,∠CED=∠CDE,那么图中的等腰三角形共有( )个.
A.3个 B.4个 C.5个 D.6个
解:∵∠ACB=90°,∠B=36°,
∴∠A=54°,
∵BC=BD,
∴∠CDB=∠DCB=72°,
∴∠ECB=36°,∠ACE=54°,
∴CE=BE,AE=CE,
∴△BCD,△CDE,△CEB,△ACE都是等腰三角形,
B
课堂小测
3.如图,将一张长方形纸片ABCD按图中方式进行折叠,若AE=3,AB=4,BE=5,则重叠部分的面积是 .
10
解:∵长方形纸片ABCD按图中那样折叠
∴∠1=∠2,
而∠1=∠3,
∴∠2=∠3,
∴ED=EB,
又∵AE=3,AB=4,BE=5,
∴DE=5,
∴重叠部分△BDE的面积=
DE×AB=
×5×4=10.
课堂小测
4.在△ABC中,∠BAC=90°,∠C=30°.用无刻度的直尺和圆规在BC边上找一点D,使△ACD为等腰三角形.下列作法正确的有 个.
3
课堂小测
5.如图:△ABC的边AB的延长线上有一个点D,过点D作DF⊥AC于F,交BC于E,且BD=BE,求证:△ABC为等腰三角形.
证明:∵DF⊥AC,
∴∠DFA=∠EFC=90°.
∴∠A=∠DFA﹣∠D,∠C=∠EFC﹣∠CEF,
∵BD=BE,
∴∠BED=∠D.
∵∠BED=∠CEF,
∴∠D=∠CEF.
∴∠A=∠C.
∴△ABC为等腰三角形.
脑筋急转
6.如图,在△ABC中,∠A=60°.BE,CF交于点P,且分别平分∠ABC,∠ACB.
(1)求∠BPC的度数;
(2)连接EF,求证:△EFP是等腰三角形.
(1)解:∵∠A=60°,
∴∠ABC+∠ACB=180°﹣∠A=120°,
∵BE平分∠ABC,CF平分∠ACB,
∴∠ABE=∠CBE=
ABC,
∴∠CBE+∠BCF=
∠ABC+
ACB=
=60°,
∴∠BPC=180°﹣(∠CBE+∠BCF)=180°﹣60°=120°;
脑筋急转
6.如图,在△ABC中,∠A=60°.BE,CF交于点P,且分别平分∠ABC,∠ACB.
(1)求∠BPC的度数;
(2)连接EF,求证:△EFP是等腰三角形.
在△FBP和△QBP中,
∴△FBP≌△QBP(SAS),
∴FP=QP,∠BFP=∠BQP,
∵∠A=60°,∠FPE=∠BPC=120°,
∴∠AFP+∠AEP=360°﹣60°﹣120°=180°,
∴∠BFP+∠CEP=180°,
∵∠CQP+∠BQP=180°,
∴∠CEP=∠CQP,
在△CQP和△CEP中,
∴△CQP≌△CEP(AAS),
∴EF=QP,
∵FP=EP,
∴△EFP是等腰三角形.
证明:在BC上截取BQ=BF,连接PQ,
课堂总结
等腰
三角形
判定
综合应用
如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)
将等腰三角形的性质和判定综合应用在解决实际问题中
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
